× × pm B = B = BA⋅ =
Anuncio

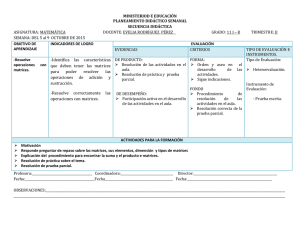
Multiplicación de matrices Definición: Sean El A =[ a ij ] una matriz de m × n B =[ bij ] una matriz de n × p producto de las matrices m × p definida por A ⋅ B =[ cik ] A y B es la matriz n donde c = ∑ a ⋅b ik j =1 ij Ejemplos: 1) Sean entonces 2) 1 2 4 A = 3 A⋅B y 0 − 1 8 B = 5 1 ⋅ 0 + 2 ⋅ 5 1 ⋅ (−1) + 2 ⋅ 8 10 = = 3 ⋅ 0 + 4 ⋅ 5 3 ⋅ (−1) + 4 ⋅ 8 20 2 1 3 7 A = Sean 4 6 y 15 29 3 1 9 7 0 B = 5 entonces 2 ⋅ 3 + 1 ⋅ 5 2 ⋅ 1 + 1 ⋅ 7 2 ⋅ 9 + 1 ⋅ 0 11 9 18 A ⋅ B = 3 ⋅ 3 + 7 ⋅ 5 3 ⋅ 1 + 7 ⋅ 7 3 ⋅ 9 + 7 ⋅ 0 = 44 52 27 4 ⋅ 3 + 6 ⋅ 5 4 ⋅ 1 + 6 ⋅ 7 4 ⋅ 9 + 6 ⋅ 0 42 46 36 jk de Observaciones: 1) 2) 3) En general, si Si A ⋅ B y distinto. A⋅B A ⋅ B está definida B ⋅ A no lo está. B ⋅ A están definidas, en general son de tamaño B ⋅ A están ambas definidas y además tienen el mismo tamaño ( A y B son cuadradas de igual tamaño) , en Si y general son distintas , o sea, el producto de matrices NO es conmutativo). Definición: A ⋅ B = B ⋅ A entonces se dice que A A y B son matrices conmutativas. Si y B conmutan o que Ejemplo: Sean A A⋅B 1 1 = 0 1 =B⋅ A y 2 5 2 B = 0 2 7 = 0 2 entones A y B conmutan. Propiedades: α ∈ ℜ y para toda B y C de n × p : Para todo matrices 1) matriz A A ⋅(B + C ) = A ⋅ B + A ⋅C de m×n y 2) α ( A ⋅ B ) = A ⋅ (α B ) = (α A ) ⋅ B Propiedad: A⋅ In =In ⋅ A de orden n . = Propiedad: Para toda matriz p×r A de A , donde m×n In es la matriz identidad B , de n× p A ⋅ (B ⋅C ) = ( A ⋅ B) ⋅C Propiedad: Para toda matriz (A ⋅ B) t A de m×n y B de n× p t t ⋅ B A = Definición: Sea A Se define una matriz cuadrada de orden A 0 = In y A m n , m ∈ℵ = A m −1 ⋅A , , C de Ejemplo: A Sea A 1 A 2 A 3 = 11 − 25 =4 −9 A = A⋅A = 2 A ⋅A 11 − 25 ⋅ − 9 =4 11 − 25 21 − 50 4 − 9 = 8 − 19 21 − 50 11 − 25 31 − 75 ⋅ 4 − 9 = 12 − 29 − 19 = 8