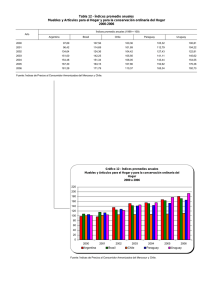
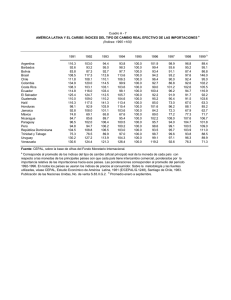
1 PROBLEMAS DE INDICES (SOLUCIONES) PROBLEMA 1: Se
Anuncio

PROBLEMAS DE INDICES (SOLUCIONES) PROBLEMA 1: Se cuenta con la siguiente información de los principales productos agropecuarios que se importan en el Perú Los valores están expresados en millones de dólares y las cantidades en toneladas. Suponga que el Instituto Nacional de Estadística e Informática desea realizar los índices de comercio exterior con base a estos datos. Calcular tales índices. 1994 1997 1998 PRODUCTOS Caña Azú. V94 96,2 Q94 338748 V97 76,7 Q97 257488 V98 138,9 Q98 499820 Arroz 64,2 246246 82,4 234214 99,0 246869 Algodón Trigo 27,1 45,7 19292 43,8 1075294 193,6 25715 1156227 78,8 176,7 44498 1221467 FUENTE: Ministerio de Agricultura – Oficina de Información Agraria Para construir el índice se dividen las importaciones en grupos, y se obtienen sendos índices parciales. Luego se determina un índice general. Para determinar las ponderaciones se utilizaran las siguientes cifras de las importaciones totales en cada período (millones de dólares) RUBROS : A. Materias primas B. Bienes de consumo a. b. c. d. e. 1994 1977 1365 1997 2657 1910 1998 2808 1884 Con base 1994, calcule para 1997 y 1998 los índices de precio (Paasche) y de quantum (Laspeyres). Calcule las relaciones de valores y efectúe las correcciones necesarias. Aplique el criterio de reversibilidad temporal al índice de 94 p I 97 materias primas ya calculado. Para el subgrupo materias primas (A-1), calcule el índice de quantum para 1998, con base 1997, utilizando la fórmula de Laspeyres. Empalme este resultado con el obtenido para 1997 con base 1994. Compare el resultado con el cálculo directo para 1998 con base en 1994. Utilizando los datos correspondientes al grupo “materias primas”, compruebe que, por ejemplo para el año 1995, el índice de Laspeyres no muestra los tipos de sesgos mencionados por Fisher: un índice de tipo aritmético tiene un sesgo hacia arriba; uno armónico posee un sesgo hacia abajo. 1 La comprobación puede realizarse por medio de las fórmulas: A− L I ∑pq I = A− L p ∑ p pq pt ∑ p p0q0 0 = p0 q0 t t 0 t 0 t SOLUCIÓN: Con estos datos hacemos los siguientes cálculos necesarios: PRODUCTOS Caña de Azúcar Algodón total materias primas Arroz Trigo total bienes de consumo P94 0,00028 0,00140 0,00026 0,000043 P97 P94*Q97 P94*Q98 0,00030 73,1 141,94 0,00170 36,1 62,51 109,2 204,4 0,00035 61,1 64,36 0,00017 49,1 51,91 110,2 116,3 Luego, podemos agrupar el cuadro en 2 grupos: GRUPOS 1994 Materias primas 1977 59,2 Bienes de consumo 1365 40,8 total 3342 100 1997 2657 58,2 1910 41,8 4567 100 1998 2808 59,8 1884 40,2 4692 100 Obtenemos los índices de precio y cantidad para 1997 y 1998: 2 PARA 1997: PARA 1998: P IP97 = A. ∑ P97Q97 ∑ P94Q97 P IP97 = A. PRECIOS: PRECIOS: Materias primas: Materias primas: PIP97 PIP98 = 120,5 = 110,30 109,2 = 217,7 = 106,48 204,4 B. consumo: PIP97 ∑ P98Q98 ∑ P94Q98 B. consumo: PIP98 = 276 = 250,48 = 275,7= 250,48 110,2 ⇒ Indice General: 110,30*58,2+250,48*41,8=168,91 116,3 ⇒ Indice General: 106,48*59,8+250,48*40,2=158,93 CANTIDAD: CANTIDAD: L IQ97 = ∑ Q97 P94 ∑ Q94 P94 L IQ98 = Precios: ∑ Q98P94 ∑ Q94 P94 Precios: IQ97 = 109,2=88,6016 L L IQ98 = 204,4=165,82 123,3 123,3 B, consumo: B, consumo: IQ97= 110,2= 100,275 L L 109,9 ⇒ Indice General: 88,60*59,2+100,28*40,8=93,37 IQ98 = 116,3= 105,80 109,9 ⇒ Indice General: 165,82*59,2+100,28*40,8=141,30 Nota: Las preguntas b) al e) quedan como ejercicio para el lector. 3 PROBLEMA 2: Se dispone de los siguientes índices de precios reales de las principales exportaciones tradicionales agrupados según los siguientes rubros (Año Base 1990=100): Pesqueros: Harina de pescado, aceite de pescado Agrícolas: Algodón, Azúcar, Café, y otros Mineros: Cobre, Estaño, Hierro, Oro, Plata Refinada, plomo, Zinc, y otros Petróleo y derivados. Solución a) Primeramente calculamos la venta total de cada producto para el periodo 1990-1998 y también el porcentaje total que constituye cada producto de las exportaciones totales: EXPORTACIONES AÑOS Pesqueras Agrícolas Mineras 1990 1991 1992 1993 1994 1995 1996 1997 1998 Total Ventas % del Total 345 453 435 581 780 787 909 1126 410 5826 0,20 174 202 112 83 247 346 297 472 323 2256 0,08 1481 1535 1820 1473 1971 2616 2654 2731 2734 19015 0,65 Petroleo y derivados 258 169 196 182 165 241 353 376 224 2164 0,07 29261 Luego utilizamos los porcentajes de la última fila, para ponderar los indices parciales (los índices de cada producto), para finalmente obtener el índice general de precios reales para las exportaciones de cada año: AÑOS 1990 1991 1992 1993 PONDERACIONES INDICE GENERAL 0,20 0,08 0,65 0,07 100,0 100,0 100,0 100,0 100,0 127,3 104,0 86,9 63,2 94,5 134,6 82,0 85,3 64,9 93,4 111,3 79,0 70,5 66,1 79,0 4 1994 1995 1996 1997 1998 100,7 114,6 144,6 154,8 177,4 173,9 150,9 119,9 194,6 146,5 83,0 93,6 81,6 82,4 71,5 67,3 72,1 85,9 77,8 47,9 92,4 100,6 97,4 105,1 96,6 NOTA: Dado que todos los índices parciales se encuentran en un mismo año base, entonces no hay problema. En caso de que existieran índices con base distintas, todos tienen que pasarse a un mismo año base antes de realizar las ponderaciones y hallar los índices reales totales. Solución b) De acuerdo a la teoría, el producto de los índices de precios y de cantidad, nos da el Indice de valor, que multiplicado con el valor de las importaciones nominales en el año base de estos índices, nos debe estimar el valor de las importaciones para el año requerido. De acuerdo a esto: 1812964946*182,6=33104739,9 Y luego estimamos las importaciones para 1995: 666,22 ∗ 33104739,9=22055039826,7 Luego estimamos en que porcentaje difiere esta cifra del valor que se obtuvo en 1995 de 22048554488 22048554488-22055039826,7 =-0,03 22048554488 De acuerdo a esto observamos que las importaciones estimadas superan en apenas 0,03 porciento a la cifra que se obtuvo en la realidad, por lo que si existe coerencia de lo teórico con lo empirico, y los indices deben ser correctos. Nota: se puede tomar como un limite permisible de diferencia a un 5% del valor teórico con lo empírico, por encima del cual sería cuestionable la veracidad de los datos utilizados para los cálculos. 5 PROBLEMA 3: El tipo de cambio Oficial (promedio compra-venta) en el mes de julio de los años 1991, 1995, 1999 fue 0.82, 2.23, y 3.32 nuevos soles por dólar respectivamente. De acuerdo a esto halle La tasa de variación del tipo de cambio oficial para los periodos 1991-1995, y 1995-1999. Solución: Tipo de cambio en el mes de julio es: Año 1991 1995 1999 Tipo de Cambio T. de vari. Acum. 0,82 2,23 3,32 Var.% 28,4 10,5 171,951 48,879 PROBLEMA 4 A continuación se tienen los datos de exportación de un grupo de productos representativos de la economía peruana para los años de 1979 y 1994: EXPORTACIONES EN AÑO BASE 1979 Y EN AÑO BASE 1994 Millones de Dólares Nominales 1979 1994 % Productos Tradicionales Harina de Pescado Valor millones de $ Volumen miles de TM Precios $ / TM $ / TM Café Valor millones de $ Volumen miles de TM Precios $ / qq $ / TM Cobre % 1994/197 % 9 Promedi o Anual 2817 17,8 3162,5 7,1 12,26 0,8 256 657 389,7 389,6 1,6 713,3 1,6 2221,2 321,2 178,63 238,08 -17,58 7,1 8,5 -1,3 245 70 162,1 3500 1,6 207 68,3 139,4 -15,51 -2,43 -14,00 -1,1 -0,2 -1,0 6 0,5 Valor Volumen Precios millones de $ miles de TM $ / lb $ / TM 674 373 81,9 1807,0 Plata Refinada Valor millones de $ 234 miles de Oz. Volumen 24807 Tr. Precios $ / Oz. Tr. 9,4 $ / Oz. Tr. 9,4 Plomo Valor millones de $ 294 Volumen miles de TM. 164 Precios $ / lb. 81 $ / TM 1792,7 Petróleo y Derivados Valor millones de $ 648 Volumen miles de Bs. 23570 Precios $ / Bs. 27,4 $ / Bs. 27,5 Otros Productos No Tradicionales / 823,6 387 96,5 1,8 22,20 3,75 17,83 1,3 0,2 1,1 1,5 97,9 0,2 -58,16 -5,6 18800 -24,21 -1,8 5,2 -44,68 -3,9 1,9 195,1 180 49,2 0,4 -33,64 9,76 -39,26 -2,7 0,6 -3,3 4,1 164,9 14000 11,8 0,4 -74,55 -40,60 -56,93 -8,7 -3,4 -5,5 466 3,0 960,7 2,1 106,16 4,9 674 4,3 1214,6 2,7 80,21 4,0 22,1 4377,1 9,8 25,38 1,5 184,02 7,2 TOTAL EXPORTACIONES 3491 export. PBI 4,3 22,1 9,8 PBI EN millones de 15785 DOLARES $ 44832 Suponga que estos productos constituyan el grupo representativo de exportación del Perú. a) A continuación se pide calcular los índices de precio y quantum (de cantidad) para las Exportaciones de 1994 (año base=1979) de la Economía Peruana 7 Sugerencia: Para los índices de precio utilice la formula de Paasche, y para los índices Quantum la formula de Laspeyres: b) Sí el índice de precios del PBI para 1994 fue de 2405088417.8, y el índice volumen físico fue de 115.6076, que se puede decir sobre la participación del valor de las exportaciones Solución: A continuación se muestra los cálculos para el índice de precios de las exportaciones: INDICES DE PRECIO PARA LAS EXPORTACIONES DE 1994 AÑO BASE 1979 GRUPOS SUBPRODUCTOS PRODUCTOS TRADICIONALES INDICE DE INDICE DE PRERELATIVO PRECIOS CIOS RELATIVO DE (BASE 1979=100) (EN SOLES) PRECIOS Y P79Q94 W94 P94/P79 PAASCHE RELATIVO DE PRECIOS (EN SOLES) P94/P79 (P94/P79)*W94 TOTAL 2686840,64 100,00 81,95 802 257 115,62 33,36 Harina de Pescado 865601,64 32,22 0,82 26,55 806 875 929,39 33,55 Café 239050,00 8,90 0,86 7,65 841 862 932,76 35,00 Cobre 699309,00 26,03 1,18 30,67 1 153 466 645,39 47,96 Plata Refinada 176720,00 6,58 0,55 3,64 541 548 203,00 22,52 Plomo 322560,00 12,01 0,61 7,29 594 623 012,64 24,72 Petróleo y Derivados 383600,00 14,28 0,43 6,15 421 592 691,44 17,53 TIPO DE CAMBIO: TC 1979 0,000000224 INDICE DE PRECIOS EN SOLES 73 TC 1994 2,2 BASE 1979=100 8 TIPO DE TC94/TC79 CAMBIO RELATIVO: Indices de precios del PBI 9789525,208 802257115,62 2405088418 En la última columna observamos el relativo de precios A continuación se muestra los cálculos de índice de cantidad: INDICES DE CANTIDAD PARA LAS EXPORTACIONES DE 1994 AÑO BASE 1979 GRUPOS Y SUBPRODUCTOS PRODUCTOS TRADICIONALES RELATIVO PONDERACIONES DE CANTIDAD W79 Q94/Q79 INDICE DE CANTIDADES (BASE =1979) INDICES DE CANTIDADES RELATIVAS RESPECTO AL PBI LASPEYRES (Q94/Q79)*W79 TOTAL 100 114,37 98,93 Harina de Pescado 10,89 3,38 36,81 292,44 Café 10,42 0,98 10,17 84,40 Cobre 28,67 1,04 29,74 89,75 Plata Refinada 9,95 0,76 7,54 65,55 Plomo 12,51 1,10 13,73 94,94 Petróleo y Derivados 27,56 0,59 16,37 51,38 Índice de volumen físico del PBI 115,6076 9 PROBLEMA 5: Calcule el índice de quantum para 1998, con base 1994, mediante la fórmula de Laspeyres, sobre la base de los siguientes datos de comercio exterior (exportaciones de productos agrícolas en dólares y toneladas): Solución: Efectuando los cálculos necesarios en las últimas 2 columnas: V94 4929,0 188165,5 32662,0 79256,3 Q94 2248 62094,0 73563 72367 V98 3991,0 280641,2 26862,6 113490,1 Q98 P94 P94*Q98 P94*Q94 1632 2,19 8750,73 4929,00 114894 3,03 850436,21 188165,46 60230 0,44 11926,98 32661,97 78771 1,10 124294,37 79256,34 305012,8 995408,30 305012,77 A continuación hacemos uso de la formula de Laspeyres para obtener el indice de cantidad: 98 Q94 = ∑ P94 * Q98 = 995408,30 = 3,26 ∑ P94 * Q94 305012,77 PROBLEMA 6: Los índices de volumen físico y de precios para la exportación en el Perú durante el periodo 1979-1985 (año base1979=100), fueron los siguientes: Años 1979 1980 1981 1982 1983 1984 1985 a. b. INDICES Precio Volumen físico 100,0 100,0 151,0 90,8 203,3 88,2 309,8 93,6 724,0 83,9 1521,9 91,5 4281,9 95,6 Fuente: Instituto Nacional de Estadística e Informática Suponga que se trata de índices de base fija (1979). Calcule entonces los correspondientes índices de base variable. Suponga que se trata de índices de base variable. Calcule entonces los correspondientes índices de base fija (1979). 10 Solución: Para el cálculo de los índices de base variable y fija, utilizamos las formulas a, y b respectivamente: a. IT = It I t −1 b. IT = I t * I t −1 Las 2 últimas columnas de cada cuadro muestran los cálculos respectivos de índice de Base variable(asumiendo índices de base fija) y fija (asumiendo índices de base variable). PARA LOS ÍNDICES DE PRECIOS AÑOS Indices a b. 1979 100,0 1980 151,0 151,0 151,0 1981 203,3 134,6 307,0 1982 309,8 152,4 629,8 1983 724,0 233,7 2243,0 1984 1521,9 210,2 11018,6 1985 4281,9 281,4 65166,2 PARA LOS INDICES DE VOLUMEN FISICO Años Indices a. b. 1979 100,0 1980 90,8 90,8 90,8 1981 88,2 97,1 80,1 1982 93,6 106,1 82,6 1983 83,9 89,6 78,5 1984 91,5 109,1 76,8 1985 95,6 104,5 87,5 11 PROBLEMA 7: Los índices de cantidad de los principales productos tradicionales de exportación para el Perú (con base 1979=100) son de 122,2 si se usa la fórmula de Paashe y de 114,37, si se emplea la de Laspeyres. En base a estos datos, calcule el índice Fisher, y el índice de Sidwick Drobish. Solución: Tenemos los siguientes datos: LQ Indice de Laspeyres: Indice de Paashe: PQ = 114,4 = 122,2 Las fórmulas de los índices de Fisher y Sidwick Drobish son: FQ= 118 L Q* P Q SD Q = L Q+ P Q 2 Haciendo los remplazos respectivos tenemos: SD Q = F Q = 114,4 * 122,2 = 118,2 114,4 + 122,2 = 188,285 2 PROBLEMA 8: La Economía de un determinado país muestra los siguientes índices de Importación: V= Relación de valores=130,25 LIP = Laspeyres – precios =192 FIP = Fisher – precios = 152 En base a esta información, determine los índices de cantidades de Laspeyres y de Paasche. Solución: Por datos tenemos lo siguiente: V = 130 ,3 LI = 192,0 F I = 152,0 El índice de volumen es igual: V = L Q∗P Q = P Q∗L I 12 Remplazando valores: 130,3= P Q ∗ 192,0 ⇒ PQ El índice de Fisher es igual: F = 67,83854167 = Indice de Paasche I= L I *P I Remplazando valores: 152,0 = 192∗ P I 130,3= L Q * 120,3 23104,0 = 192∗ P I ⇒ LQ ⇒ PI = 120,3 = 108,2409972 = Indice de Laspeyres PROBLEMA 9: Con los siguientes valores de exportación e importación en valores corrientes y reales para la economía peruana 1995-1998, determine los términos de intercambio. Solución: Primeramente trabajamos con los índices de exportación e importación por separado; para lo cual los separamos de la siguiente manera: AÑOS 1995 1996 1997 1998 EXPORTACIÓN PnQn 15280074200 18067065900 22446576505 21454635625 IMPORTACIÓN PoQn 1061,9 1176,0 1329,2 1374,4 PnQn 22048554488 24978577430 28749307972 30836013906 PoQn 1216,2 1223,0 1347,6 1350,6 Luego de esto en el siguiente cuadro mostramos los indices de precio de la exportación y la importación que se halla empleando la formula que se muestra debajo, y además en el último cuadro se muestra la relación de términos de Intercambio, que es igual a la relación de estos índices de precios AÑOS IE IM TÉRMINOS DE INTERCAMBIO 1995 1996 1997 1998 14388965,56 15363412,56 16887155,91 15610183,08 18129649,5 20424521,8 21333868,6 22832189,8 79,37 75,22 79,16 68,37 Indice de precios = PI = ∑ PnQn ∑13P0Qn PROBLEMA 10: Los índices de Volumen físico (IVF) para la exportación e importación de la Economía Peruana en 1990 fueron de 74,6 y 85,4 respectivamente (Base 1979=100). Para 1996 fueron de 121,5 y 183,6. De acuerdo a esto: a. Calcule las tasas anuales que implican dicha variación, tanto de la importación como de la exportación, y compare dichas tasas. Comente. b. Si suponemos que se hubiera mantenido el ritmo de crecimiento para cada uno de ellos. Estime los IVF de exportación e Importación que pudo esperarse para 1999, y compare de ser posible con los índices reales de Comercio exterior para ese mismo año. Solución: a) tasa implícita de variación de las Exportaciones: 6 74,6(1+ iX) =121,5 iX = 0,09 ⇒ iX >0 implica una tasa de crecimiento en las exportaciones tasa implícita de variación de las Importaciones: 6 ⇒ iM = 0,14 85,4(1+ iM) = 183,6 iM >0 implica una tasa de crecimiento en las importaciones De aquí vemos que (iX< iM ). De acuerdo se puede decir que durante el periodo 1990-1996; si bien es cierto las exportaciones (en términos de cantidad) crecieron; lo hicieron a un ritmo menor que con el que crecieron las importaciones; lo que al final pudo repercutir como un efecto negativo en la balanza comercial o cuenta corriente de la economía Peruana. b) Primero estimamos la tasa de crecimiento de las exportaciones de 19961999, que implica 3 años: (1+ iX)3=1,28 luego, el IVF de exportación estimado para 1999 será igual: IVF1999=1,28*IVF1996 =1,28*121,5=155,8164759 14 Luego estimamos la tasa de crecimiento de las exportaciones de 1996-1999, que también implica 3 años: (1+ iM)3=1,48 luego, el IVF de importación estimado para 1999 será igual: IVF1999=1,48*IVF1996 =1,48*183,6=271,271537 Luego estos datos debemos compararlo con los valores reales que se obtuvieron en 1999. 15