problemas intercambiadores
Anuncio
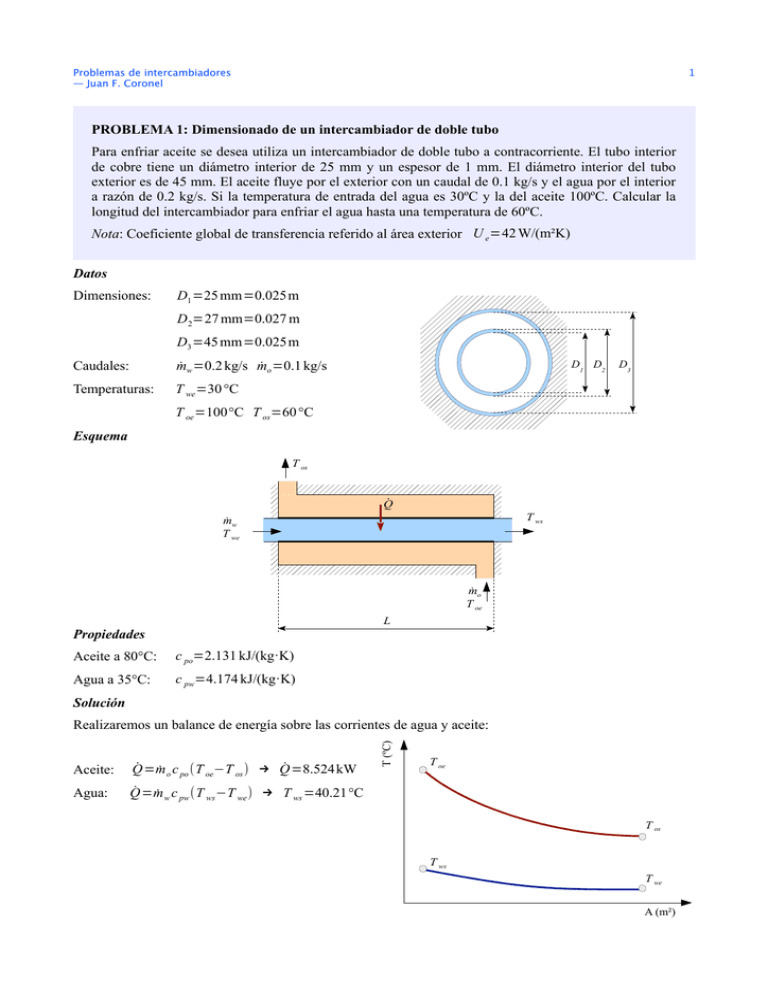
Problemas de intercambiadores — Juan F. Coronel 1 PROBLEMA 1: Dimensionado de un intercambiador de doble tubo Para enfriar aceite se desea utiliza un intercambiador de doble tubo a contracorriente. El tubo interior de cobre tiene un diámetro interior de 25 mm y un espesor de 1 mm. El diámetro interior del tubo exterior es de 45 mm. El aceite fluye por el exterior con un caudal de 0.1 kg/s y el agua por el interior a razón de 0.2 kg/s. Si la temperatura de entrada del agua es 30ºC y la del aceite 100ºC. Calcular la longitud del intercambiador para enfriar el agua hasta una temperatura de 60ºC. Nota: Coeficiente global de transferencia referido al área exterior U e =42 W/(m²K) Datos Dimensiones: D1 =25 mm=0.025 m D 2=27 mm=0.027 m D3 =45 mm=0.025 m Caudales: ṁw =0.2 kg/s ṁo =0.1 kg/s Temperaturas: T we =30 °C D1 D2 D3 T oe =100°C T os =60 °C Esquema T os Q̇ T ws ṁw T we ṁo T oe L Propiedades Aceite a 80°C: c po=2.131 kJ/(kg·K) Agua a 35°C: c pw=4.174 kJ/(kg·K) Solución Aceite: Q̇=ṁ o c po (T oe−T os ) → Q̇=8.524 kW Agua: Q̇=ṁ w c pw (T ws −T we ) → T ws =40.21°C T (ºC) Realizaremos un balance de energía sobre las corrientes de agua y aceite: T oe T os T ws T we A (m²) Problemas de intercambiadores — Juan F. Coronel 2 Ecuación de transmisión de calor a través de la pared interna del intercambiador: Q̇=U e Ae (T o−T w )=U e Ae Δ T med La diferencia de temperatura media, para el caso del doble tubo a contracorriente, puede demostrase que es igual a la diferencia de temperatura logarítmica media (DTLM): Δ T med = Δ T lm= Δ T e − Δ T s (T oe −T ws )−(T os −T we ) = ΔTe T −T ws ln ln oe ΔT s T os −T we ( ) ( ) Para nuestro caso: Δ T lm= 43.2°C Si sustituimos en la ecuación de transmisión de calor el área exterior por su valor tenderemos: Q̇=U e π L D 2 Δ T lm Y despejando la longitud: L=55.6 m Solución usando el método efectividad-NTU: La definición de la efectividad es la siguiente: ε= Q̇ Q̇ max El calor máximo transferible se define en función del fluido con menos capacidad calorífica: Q̇ max =( ṁ c p )min Δ T max Para nuestro caso el fluido con menor capacidad calorífica es el aceite y por tanto: Q̇ max =ṁ o c po (T oe −T we )=14.92 kW → ε =0.571 (57.1% ) En la colección de tablas y gráficas podemos encontrar las gráficas y expresiones que relacionan la efectividad con el NTU para diferentes tipos de intercambiadores, para el caso del doble tubo a contracorriente la expresión es: NTU = ( 1 ε −1 ln C r −1 ε C r −1 ) Donde: ( ṁ c p )min ṁo c po = =0.255 ( ṁ c p )max ṁ w c pw • C r= • NTU = U e Ae U e Ae = ( ṁ c p )min ṁ o c po Si usamos la gráfica 1.2 NTU = 0.95 y usando la expresión anterior NTU = 0.925, usaremos el valor de la expresión por ser más exacto. Despejando de la expresión del NTU calculamos la longitud necesaria: NTU = U e π D2 L → ṁ o c po L=55.5 m