27 ϕ λ ϕ λ ϕ λ ϕ

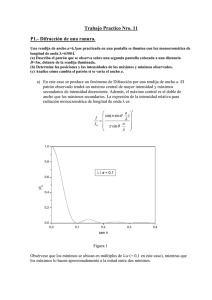
UNIVERSIDAD DE PAMPLONA
Facultad de Ciencias Básicas
Departamento De Física
Laboratorio de Oscilaciones y Ondas
27
DIFRACCIÓN DE ONDAS LUMINOSAS
OBJETIVOS
•
Estudio del fenómeno de la difracción de Fraunhhofer con base en el experimento de Young.
•
Reconocimiento de las principales partes del esquema de la doble hendija de Young para
observar la interferencia y la difracción utilizando una fuente láser de He-Ne de gran coherencia.
•
Medición de los parámetros b, d, L de dicho esquema y determinación de la longitud de la onda
luminosa.
El esquema que utilizaremos para la observación de la difracción es el de la Figura 1: es la doble hendija
de anchos iguales b y con una distancia entre hendijas vecinas d. Un haz paralelo de la fuente láser de
He-Ne (1) ilumina la pantalla (2) que posee dos hendijas angostas (3 y 4), cuyas longitudes son mayores
que la sección transversal del haz incidente.
Según el principio de Huygens: cuando la onda plana incide sobre las dos hendijas, éstas se convierten
en fuentes de ondas secundarias, que se propagan en todas direcciones o sea la luz se difracta en las
hendijas, como se muestra en la Figura 1, las ondas difractadas son coherentes, debido a que ellas se
formaron por medio de la división del frente de onda de una onda plana, y por lo tanto ellas pueden
interferir en la región donde se superponen (punto P de la pantalla 5).
La difracción de Fraunhhofer solo se observa en haces paralelos, por lo que en este esquema la
distancia de observación L hasta la pantalla 5, es mucho mayor que el ancho b y la distancia de
separación d entre hendijas con una longitud de onda dada, y d es de un valor cercano a b: L>>b2/λ.
En este caso los rayos que van hacia la pantalla 5 son prácticamente paralelos (Ver la práctica de
interferencia, figura 1).
En el cálculo de la distribución resultante de las intensidades en la pantalla 5 (se ilustra en la figura 3), se
deben tener en cuenta las distribuciones de las intensidades debidas a la difracción en cada hendija y la
distribución de intensidades debida a la interferencia de las ondas coherentes provenientes de las
hendijas 3 y 4.
Para observar la difracción se debe tener en cuenta que las dimensiones de las hendijas o del obstáculo
deben ser del mismo orden de la longitud de la onda de la fuente de luz.
Las Condiciones para el mínimo de intensidad, debidos a la difracción en una hendija, llamados también
mínimos principales, se obtienen a partir de la expresión.
b sen ϕ k = kλ ; k = 1 , 2 , 3 K
(4)
Donde:
ϕK – es el ángulo de difracción. En k = 0, se tiene el máximo de la difracción.
Las Condiciones para los máximos principales son:
b sen ϕ 1 = ± 1.43λ ; b sen ϕ 2 = ± 2.46 λ ; b sen ϕ 3 = ± 3.47 λ K
(5)
Las posiciones de los máximos y los mínimos de cada hendija no dependen de las posiciones de las
hendijas con relación al eje del haz luminoso, porque estas posiciones están determinadas por la
dirección de propagación de la mayor parte de la luz que se difracta. Por eso las hendijas 3 y 4 dan
Escrito por: Alberto Patiño Vanegas, Heriberto Peña Pedraza
UNIVERSIDAD DE PAMPLONA
Facultad de Ciencias Básicas
Departamento De Física
Laboratorio de Oscilaciones y Ondas
28
patrones iguales de difracción, los cuales se superponen el uno sobre el otro, amplificándose el uno con
el otro. En la figura 3, se muestran los efectos combinados de difracción e interferencia de las ondas
luminosas debidas a las dos hendijas 3 y 4, la curva continua interior corresponde a la interferencia
resultante de los máximos y mínimos principales determinados por las formulas (1) y (2), se puede ver
que dicha curva esta siendo modulada en amplitud por los efectos de la difracción de las ondas en las
respectivas rendijas, o sea que ella corresponde a la distribución de las intensidades de los máximos y
mínimos principales de difracción dados por la formula (4 y 5).
En la figura 3 se observa que casi todo el flujo luminoso difractado se concentra en el máximo central
(90%), el patrón de difracción restante es muy débil y casi no se observa. Si d mayor que b, en los
límites de ángulo ϕ1 se disponen varios máximos de interferencia. Si d/b =n (n entero) de las formulas (4
y 5) obtenemos:
sen ϕ 1 =
λ
b
= sin θ n =
nλ
d
(6)
Por lo tanto los máximos de interferencia de órdenes superiores coinciden con los mínimos de difracción
de primer orden y son apagados. De tal forma que entre los mínimos de difracción de primer orden se
acomodan 2n -1 máximos de interferencia, o sea:
b=
d
n
(7)
DETERMINACIÓN DEL ANCHO b Y LA SEPARACIÓN ENTRE HENDIJAS d, CONOCIENDOλ.
1. Realizar el montaje de la figura 1.
2. Encender el láser, posicionar perpendicularmente la lámina a una distancia del láser tal, que el
haz de luz cubra el ancho de las dos hendijas, colocar la pantalla al final del cuarto oscuro.
3. Reposicionar el montaje lo necesario para poder visualizar un patrón de interferencia bien
definido.
4. Medir la distancia L entre el plano de las hendijas y la pantalla.
5. Medir la distancia y entre los máximos de orden cero y los de orden superior m.
6. Determine d según la formula (3).
7. Medir la distancia entre los mínimos de primer orden en el diagrama de difracción y contar el
número de máximos de interferencia que ocurren dentro de estos.
8. Determine b según las formulas (6 y 7).
9. Determine λ si se conoce de antemano d.
10. Halle el error relativo de las mediciones.
11. Conclusiones.
Escrito por: Alberto Patiño Vanegas, Heriberto Peña Pedraza