Laboratorio de Optica
Anuncio
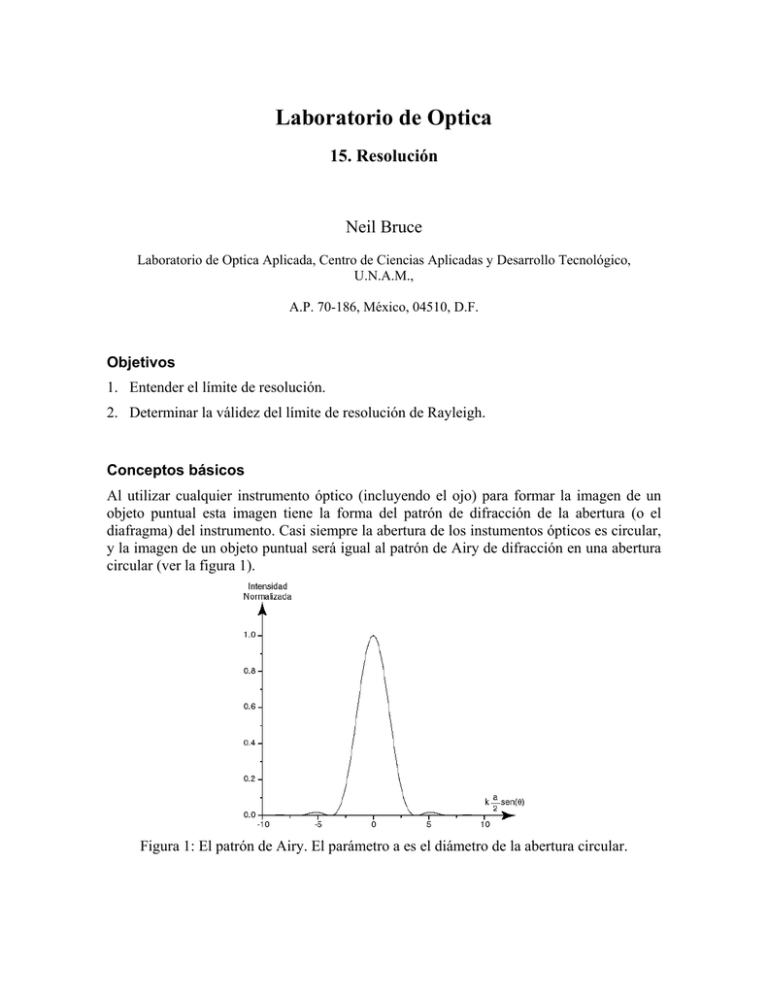
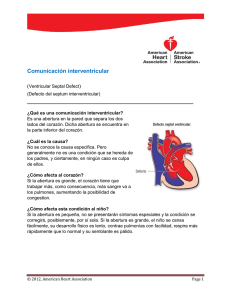
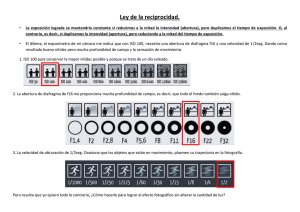
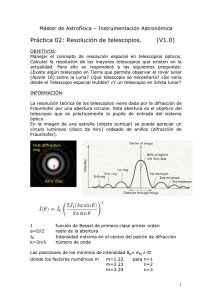
Laboratorio de Optica 15. Resolución Neil Bruce Laboratorio de Optica Aplicada, Centro de Ciencias Aplicadas y Desarrollo Tecnológico, U.N.A.M., A.P. 70-186, México, 04510, D.F. Objetivos 1. Entender el límite de resolución. 2. Determinar la válidez del límite de resolución de Rayleigh. Conceptos básicos Al utilizar cualquier instrumento óptico (incluyendo el ojo) para formar la imagen de un objeto puntual esta imagen tiene la forma del patrón de difracción de la abertura (o el diafragma) del instrumento. Casi siempre la abertura de los instumentos ópticos es circular, y la imagen de un objeto puntual será igual al patrón de Airy de difracción en una abertura circular (ver la figura 1). Figura 1: El patrón de Airy. El parámetro a es el diámetro de la abertura circular. Ahora, ¿Qué pasa cuando tenemos dos objetos puntuales (e.g. dos estrellas) en el campo de vista al mismo tiempo? En este caso tenemos que sumar las dos intensidades de los dos objetos (suponemos que son objetos de los cuales la luz es incoherente). La figura 2 muestra que pasa para diferentes separaciones de los dos objetos. Figura 2: La imagen de dos objetos puntuales separados por Δθ con k 3.18π; centro, 1.22π; y abajo, 0.32π a sen (Δθ ) = : arriba, 2 En la figura 2 se puede ver que para la separación entre los puntos de 3.18π, las dos imágenes se pueden ver separados fácilmente, o se dice que son resueltos los objetos, mientras para el último caso de la separación 0.32π, aparentemente solo hay un objeto en el campo de vista, y no hay resolución de los dos objetos. El caso intermedia es el caso del criterio de Rayleigh para el límite de resolución. Esta separación de 1.22π, corresponde al caso cuando el primer mínimo de uno de los patrones de Airy está en la posición del máximo del otro patrón. Esta separación se toma (por convención) como el límite entre los casos de resolución de dos objetos y los casos de no resolución de dos objetos. Tenemos k a sen (Δθ ) = 1.22π , entonces suponiendo ángulos pequeños, podemos escribir 2 Δθ = 1.22 λ a (1) en donde Δθ es la separación angular entre los dos objetos. Figure 3 Procedimiento experimental 1. Utilizar una lampara de luz blanca con filtros de color adecuados para iluminar un par de agujeritos en un papel aluminio. Con el ojo observa a que distancia los agujeritos no se pueden resolver para diferentes colores de la luz. Verificar si el comportamiento esta de acuerdo con la ecuación (1) y comparar los resultados para diferentes personas. 2. Ahora observa los dos agujeritos a través de un telescopio y utilizar un diafragma para ajustar la abertura del telescopio. Medir el diámetro del diafragma necesario para perder la resolución de los dos agujeritos para diferentes colores de la iluminación. Graficar λ contra a, el diámetro del diafragma para la posición de perder la resolución y comparar con la ecuación (1). ¿Sus mediciones están de acuerdo con la teoría? 3. El criterio de Sparrowe está basado en la separación para que el mínimo entre los dos objetos desaparece (ver la figura 4) y da como el límite de resolución: Δθ = 0.95 ¿Este criterio está mejor o peor que el criterio de Rayleigh basado en tus resultados? λ a Figura 4: el criterio de Sparrowe Δθ = 0.95 λ . La intensidad en el centro del patrón es a plano. Bibliografía (1) Optica, E. Hecht y A. Zajac, cap. 10