EDOs de primer orden, Practica 1
Anuncio
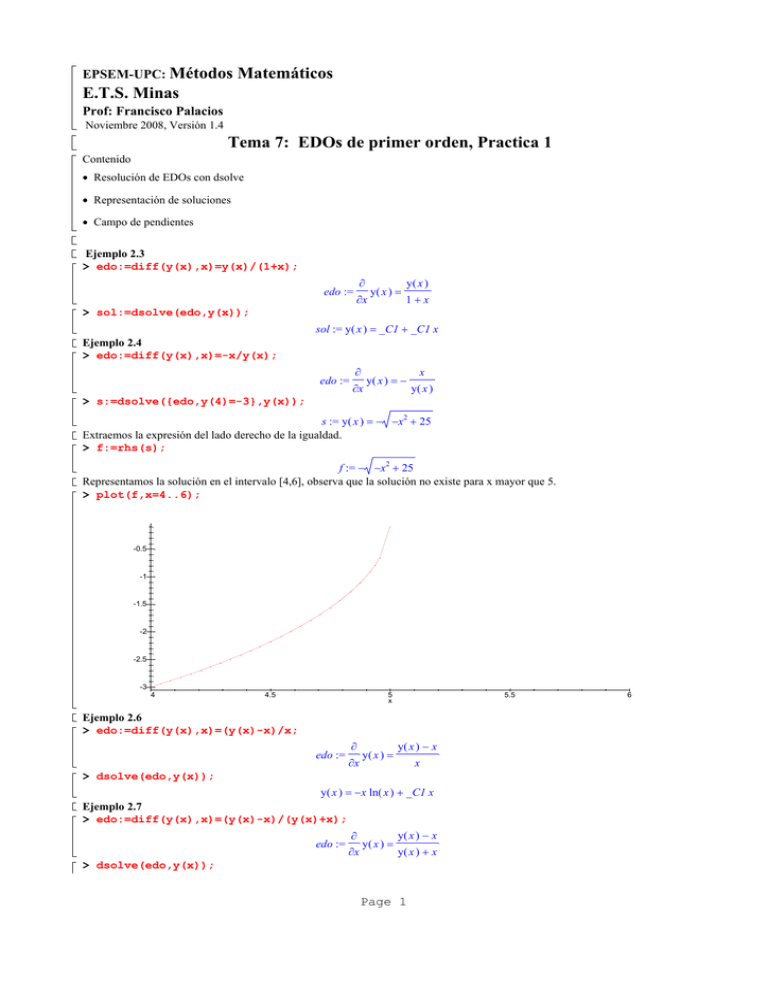
EPSEM-UPC: Métodos
Matemáticos
E.T.S. Minas
Prof: Francisco Palacios
Noviembre 2008, Versión 1.4
Tema 7: EDOs de primer orden, Practica 1
Contenido
Resolución de EDOs con dsolve
Representación de soluciones
Campo de pendientes
Ejemplo 2.3
> edo:=diff(y(x),x)=y(x)/(1+x);
edo :=
x
y( x )
y( x )
1x
> sol:=dsolve(edo,y(x));
sol := y( x )_C1_C1 x
Ejemplo 2.4
> edo:=diff(y(x),x)=-x/y(x);
edo :=
x
y( x )
x
y( x )
> s:=dsolve({edo,y(4)=-3},y(x));
s := y( x ) x225
Extraemos la expresión del lado derecho de la igualdad.
> f:=rhs(s);
f := x225
Representamos la solución en el intervalo [4,6], observa que la solución no existe para x mayor que 5.
> plot(f,x=4..6);
-0.5
-1
-1.5
-2
-2.5
-3
4
4.5
5
x
5.5
Ejemplo 2.6
> edo:=diff(y(x),x)=(y(x)-x)/x;
edo :=
x
y( x )
y( x )x
x
> dsolve(edo,y(x));
y( x )x ln( x )_C1 x
Ejemplo 2.7
> edo:=diff(y(x),x)=(y(x)-x)/(y(x)+x);
edo :=
x
y( x )
y( x )x
y( x )x
> dsolve(edo,y(x));
Page 1
6
_C1 x e
x
y( x )
arctan
x
x2y( x )2
Ejemplo 2.8
> edo:=diff(y(x),x)=(y(x)^2+y(x)*x)/x^2;
edo :=
y( x )
x
y( x )2y( x ) x
x2
> dsolve(edo,y(x));
1
ln( x )_C1
y( x )
x
Hemos obtenido una solución implícita, podemos pedir que Maple intente obtener una solución explícita con la opción .
> dsolve(edo,y(x),explicit=true);
y( x )
x
ln( x )_C1
Ejemplo 2.9
> edo:=diff(y(x),x)=-(5*x+4*y(x))/(4*x-8*(y(x))^3);
edo :=
x
y( x )
5 x4 y( x )
4 x8 y( x )3
> sol:=dsolve(edo,y(x));
sol :=
5
2
x24 y( x ) x2 y( x )4_C1
Ejemplo 2.10
> edo:=diff(y(x),x)=-(2*x+y(x))/(x+6*y(x));
edo :=
x
y( x )
2 xy( x )
x6 y( x )
> dsolve(edo,y(x));
x2y( x ) x3 y( x )2_C1
Ejemplo 2.11
> edo:=diff(y(x),x)=4*y(x)/x;
edo :=
x
y( x )4
y( x )
x
> dsolve(edo,y(x));
y( x )x4 _C1
> sol:=dsolve({edo,y(1)=3},y(x));
sol := y( x )3 x4
Extraemos la solución y la representamos en el intervalo [1,2]
> f:=rhs(sol);
plot(f,x=1..2);
f := 3 x4
40
30
20
10
1
1.2
1.4
x
Ejemplo 2.12
Page 2
1.6
1.8
2
> edo:=diff(y(x),x)=4*y(x)/x+x^5*exp(x);
edo :=
x
y( x )4
y( x )
x
x5 ex
> dsolve(edo,y(x));
y( x )x5 exx4 exx4 _C1
> sol:=dsolve({edo,y(1)=2},y(x));
sol := y( x )x5 exx4 ex2 x4
> f:=rhs(sol);
plot(f,x=1..2);
f := x5 exx4 ex2 x4
140
120
100
80
60
40
20
01
1.2
1.4
x
1.6
1.8
2
Ejemplo 2.13
> edo:=diff(y(t),t)=-y+t;
edo :=
t
y( t )yt
> dsolve(edo,y(t));
y( t )t1e( t ) _C1
> sol:=dsolve({edo,y(0)=4},y(t));
f:=rhs(sol);
sol := y( t )
f :=
et tet5
et
et tet5
et
Libreria DEtools
La librería DEtools contien herramientas para manejar ecuaciones diferenciales.
> with(DEtools);
[ DEnormal, DEplot, DEplot3d, Dchangevar, PDEchangecoords, PDEplot, autonomous, convertAlg, convertsys, dfieldplot,
indicialeq, phaseportrait, reduceOrder, regularsp, translate, untranslate, varparam ]
El comando DEplot permite dibujar campos de pendientes y soluciones.
> DEplot(edo,y(t),t=-3..3,y=-5..5,arrows=medium);
4
y(t)
2
-3
-2
-1
0
1
t
2
3
-2
-4
Poemos añadir condiciones inciales, para dibujar una o más soluciones. Para dibujar la solución que cumple y(0)=1 añadimos
[[0,1]]. Observa que cada claudátor es doble.
> DEplot(edo,y(t),t=-3..3,y=-5..5,arrows=medium,[[0,1]]);
Page 3
4
y(t)
2
-3
-2
0
-1
1
t
2
3
-2
-4
La opción color controla el color de las flechas. La opción linecolor controla el color de las curvas integrales.
A continuación, dibujamos en color azul las curvas integrales correspondientes a las soluciones con condiciones iniciales
y(0)=-2,y(0)=-1.y(0)=1,y(0)=2.
> DEplot(edo,y(t),t=-3..3,y=-5..5,arrows=medium,[[0,-2],[0,-1],[0,1],[0,2]],linecolor=bl
ue);
4
y(t)
2
-3
-2
-1
0
1
2
t
-2
-4
>
Page 4
3