Funciones y gráficas

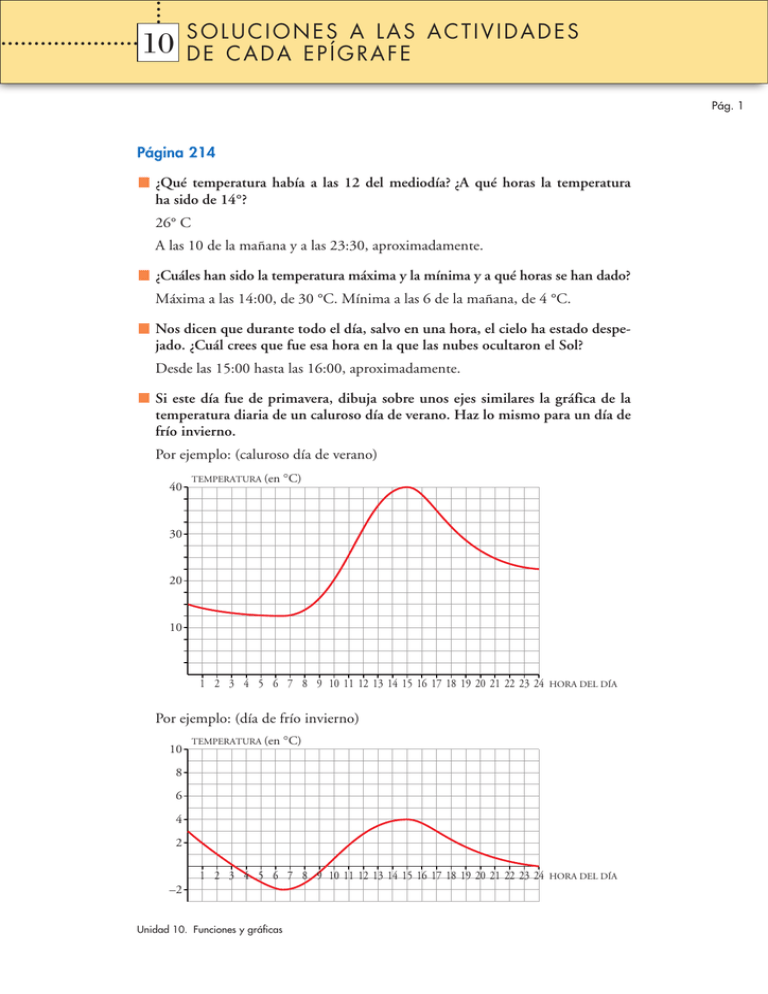
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
10
1
Pág. 1
Página 214
¿Qué temperatura había a las 12 del mediodía? ¿A qué horas la temperatura
ha sido de 14°?
26° C
A las 10 de la mañana y a las 23:30, aproximadamente.
¿Cuáles han sido la temperatura máxima y la mínima y a qué horas se han dado?
Máxima a las 14:00, de 30 °C. Mínima a las 6 de la mañana, de 4 °C.
Nos dicen que durante todo el día, salvo en una hora, el cielo ha estado despejado. ¿Cuál crees que fue esa hora en la que las nubes ocultaron el Sol?
Desde las 15:00 hasta las 16:00, aproximadamente.
Si este día fue de primavera, dibuja sobre unos ejes similares la gráfica de la
temperatura diaria de un caluroso día de verano. Haz lo mismo para un día de
frío invierno.
Por ejemplo: (caluroso día de verano)
40
TEMPERATURA (en
°C)
30
20
10
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
HORA DEL DÍA
Por ejemplo: (día de frío invierno)
10
TEMPERATURA (en
°C)
8
6
4
2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
–2
Unidad 10. Funciones y gráficas
HORA DEL DÍA
10
1
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 2
Página 215
1 Contesta razonadamente cuál de las siguientes gráficas corresponde a una
función y cuál no.
Y
Y
X
X
• La primera gráfica sí corresponde a una función: a cada valor de x le corresponde un único valor de y.
• La segunda gráfica no corresponde a una función: hay algunos valores de x a
los que les corresponde más de un valor de y.
2 Estas gráficas responden, en otro orden, a las situaciones que aparecen
debajo de ellas. Relaciona cada gráfica con la situación que refleja y di, en
cada caso, qué representan sus ejes de abscisas y ordenadas.
A
B
C
D
E
F
1 ALTURA DE UNA PELOTA QUE BOTA, AL PASAR EL TIEMPO.
4 PRECIO DE LAS BOLSAS DE PATATAS FRITAS.
2 NIVEL DE RUIDO DE UNA CALLE DESDE LAS 6
DE LA MAÑANA HASTA LAS 6 DE LA TARDE.
5 NIVEL DE AGUA EN UN PANTANO
A LO LARGO DEL AÑO.
3 TEMPERATURAS MÍNIMAS DIARIAS
EN TOLEDO, A LO LARGO DE UN AÑO.
6 DISTANCIA A LA TIERRA DE UN SATÉLITE
ARTIFICIAL, AL PASAR EL TIEMPO.
B. Abscisas: Tiempo. Ordenadas: Altura de la pelota.
D. Abscisas: Hora. Ordenadas: Nivel de ruido.
C. Abscisas: Días del año: Ordenadas: Temperaturas mínimas diarias.
A. Abscisas: Peso. Ordenadas: Precio.
E. Abscisas: Meses del año. Ordenadas: Nivel de agua.
F. Abscisas: Tiempo. Ordenadas: Distancia del satélite a la Tierra.
Unidad 10. Funciones y gráficas
10
1
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 3
Página 216
1 Observando la gráfica anterior, responde:
a) ¿A qué altura se encuentra el nido?
b) ¿A qué altura estaba en el instante 5 minutos?
c) ¿A qué altura otea para buscar caza?
d) ¿En qué instante caza al conejo?
e) ¿Cuánto tiempo pasa en el nido con su pareja y sus polluelos después de cazar al conejo?
f) ¿A qué altura volaba la paloma que caza?
g) Desde que caza a la paloma, ¿cuánto tarda en subir al nido? Halla la velocidad de subida en metros por minuto.
a) A 110 m.
b) A 60 m.
c) A 50 m.
d) A los 4 minutos.
e) Dos minutos (entre el minuto 8 y el 10).
f ) A 20 m.
g) Dos minutos (desde el minuto 15 hasta el 17).
Velocidad de subida → v = distancia = 110 – 20 = 90 = 45 m/min
tiempo
2
2
2 En unos ejes cartesianos, describe 20 minutos de vuelo de una cigüeña, desde
que sale de su nido en el campanario de una iglesia hasta que vuelve a él, después de haber intentado cazar algo (intento fallido) y de realmente haber cazado una rana.
Por ejemplo:
ALTURA
(m)
15
10
5
5
Unidad 10. Funciones y gráficas
10
15
20
TIEMPO
(min)
10
1
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 4
Página 217
3 Estas cuatro gráficas representan la temperatura máxima diaria (T) de cuatro ciudades, a lo largo del tiempo
(t), durante un cierto año:
a) A la vista de estas gráficas, ¿en cuál de estas
cuatro ciudades oscila en
menor medida la temperatura?
a
T
b
T
t
c
T
t
d
T
t
t
b) Una de estas gráficas corresponde a una ciudad de nuestro país, y otra, a
una ciudad de nuestras antípodas.
¿A qué gráficas nos estamos refiriendo? Razona la respuesta.
c) Una de las gráficas es absurda. Di cuál es y por qué.
d) Elige una escala adecuada para cada variable y gradúa cada uno de los ejes.
a) En la ciudad correspondiente a la gráfica b .
b) Nos referimos a las gráficas a y c , ya que la temperatura es alta en uno
cuando baja en el otro, y viceversa.
c) La gráfica d es absurda, porque cada vez aumenta más la temperatura sin
descender nunca y esto es un caso inexistente. La gráfica debería terminar,
aproximadamente, donde empezaba.
d) a
TEMPERATURA
b
TEMPERATURA
c
TEMPERATURA
d
30°
30°
30°
30°
20°
20°
20°
20°
10°
10°
TIEMPO
E F MAM J J A S OND
10°
TIEMPO
E F MAM J J A S OND
TEMPERATURA
10°
TIEMPO
E F MAM J J A S OND
TIEMPO
E F MAM J J A S OND
Página 219
1 Una compañía de transporte público ha recogido en una gráfica la información que tiene sobre la venta de abonos para viajar en sus líneas.
a) ¿Durante cuánto tiempo se ha hecho este estudio?
b) ¿En qué momento del año 1999 se han vendido menos abonos? ¿Y en cada
uno de los años 2000 y 2001? ¿Por qué crees que sucede esto?
c) ¿En qué momento de 2001 se produce la máxima venta? ¿A qué lo atribuyes?
d) ¿En qué periodos anuales es mayor el crecimiento en la venta de abonos?
¿Y en qué estación del año es decreciente la venta?
Unidad 10. Funciones y gráficas
10
1
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 5
700
ABONOS VENDIDOS
(miles)
600
500
400
300
200
100
E F M A M J J A S O N D E F M A M J J A S O N D E F M A M J J A S O
1999
2000
2001
a) Durante 2 años y 10 meses. (Desde enero de 1999 hasta octubre de 2001).
b) En julio de 1999, en julio de 2000 y en julio de 2001.
Se atribuye a que nadie está en la ciudad, porque se han ido de vacaciones de
verano.
c) En septiembre de 2001, ya que ha venido todo el mundo de vacaciones y se
empieza a trabajar de nuevo.
d) Desde julio hasta septiembre el crecimiento es mayor.
Desde marzo hasta julio la venta va decreciendo.
Página 220
1 Mercurio tarda 88 días en completar su órbita
100
alrededor del Sol. Su distancia al Sol oscila entre
70 y 46 millones de kilómetros.
Completa la gráfica de la distancia de Mercurio
al Sol durante 300 días.
DISTANCIA
(millones de km)
50
TIEMPO (días)
25
100
50
75
100
DISTANCIA
(millones de km)
50
TIEMPO
88
Unidad 10. Funciones y gráficas
176
264
300 (días)
10
1
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 6
2 Como sabes, el área de un cuadrado es función de
l 2.
En la gráfica aparece el área cosu lado: A =
rrespondiente a lados de hasta 2 m. Completa en
tu cuaderno la gráfica para l = 3 y l = 4 y observa
la tendencia de la superficie al aumentar el lado.
SUPERFICIE (en
m2)
10
5
SUPERFICIE (m2)
15
1
2
3
LADO (en
10
4
m)
• Al aumentar el lado, aumenta la superficie.
5
1
2
3
4
LADO (m)
Página 223
1 Disponemos de un rectángulo de cartulina de 50 cm × 20 cm y queremos fabricar una caja con tapa.
a
x
x
x
b
x
20 cm
a
b
x
a
50 cm
Obtén la expresión del volumen: V = a · b · x = … Para obtener el volumen, observa que 2a + 2x = 50 y que b + 2x = 20. Después, dando valores a x, representa la gráfica de la función V (x). ¿Cuál es su dominio de definición?
VOLUMEN (en
a = 25 – x 

b = 20 – 2x 
V = a · b · x = (25 – x)(20 – 2x) · x =
= 2x 3 – 70x 2 + 500x
cm2)
1000
750
500
250
El dominio de definición es el intervalo 0 – 10.
5
Unidad 10. Funciones y gráficas
x
10