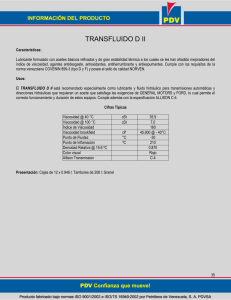
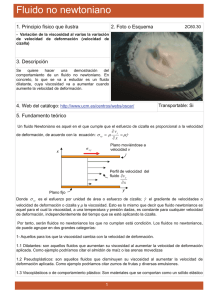
τ τ μγ = - τ = ηγ = -
Anuncio
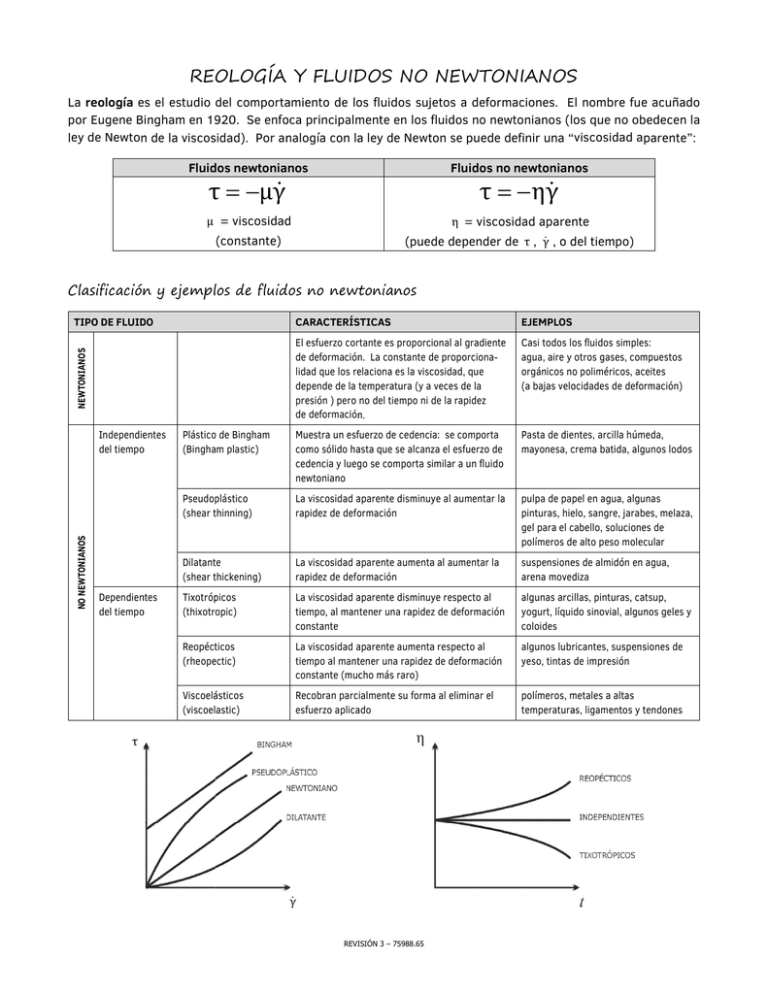
REOLOGÍA Y FLUID DOS NO NEWTO ONIANOS S La reología es L e el estudio del comporta amiento de lo os fluidos sujjetos a deformaciones. El nombre fue e acuñado p Eugene Bingham en 19 por 920. Se enfo oca principalm mente en los fluidos no ne ewtonianos (lo os que no obedecen la ley de Newton n de la viscossidad). Por an nalogía con la a ley de Newtton se puede definir una “viscosidad ap parente”: Fluid dos newtonianos Fluidos no n newtonianos τ ηγ τ μγ μ = viscosidad d η = visco osidad aparen nte (constante) (puede depender de τ , γ , o del d tiempo) TIPO DE FLUID DO CARACTERÍS STICAS EJEMPLOS NEWTONIANOS C Clasificación n y ejempllos de fluid dos no newttonianos El esfuerzo corrtante es proporccional al gradientee de deformación n. La constante de d proporcionalidad que los reelaciona es la visccosidad, que depende de la temperatura t (y a veces de la presión ) pero no del tiempo ni de la rapidez de deformación n. Casi todos lo os fluidos simpless: agua, aire y otros gases, com mpuestos orgánicos no o poliméricos, aceeites (a bajas velo ocidades de deforrmación) o de Bingham Plástico (Binghaam plastic) Muestra un esffuerzo de cedenciia: se comporta como sólido haasta que se alcanza el esfuerzo de cedencia y lueg go se comporta similar s a un fluido o newtoniano Pasta de dientes, arcilla húmeda, mayonesa, crema c batida, algunos lodos Pseudop plástico (shear thinning) t La viscosidad aparente a disminuye al aumentar laa rapidez de defo ormación pulpa de pap pel en agua, algunas pinturas, hieelo, sangre, jarabes, melaza, gel para el cabello, solucionees de polímeros dee alto peso moleccular Dilatantte (shear thickening) t La viscosidad aparente a aumentaa al aumentar la rapidez de defo ormación suspensionees de almidón en agua, arena moved diza Tixotróp picos (thixotropic) La viscosidad aparente a disminuye respecto al tiempo, al mantener una rapidez de deformación n constante algunas arcillas, pinturas, cattsup, yogurt, líquid do sinovial, algun nos geles y coloides Reopéctticos (rheopeectic) La viscosidad aparente a aumentaa respecto al tiempo al manttener una rapidezz de deformación constante (muccho más raro) algunos lubrricantes, suspenssiones de yeso, tintas de impresión Viscoeláásticos (viscoelastic) Recobran parcialmente su forma al eliminar el esfuerzo aplicaado polímeros, metales m a altas temperaturaas, ligamentos y tendones NO NEWTONIANOS Independieentes del tiempo o Dependien ntes del tiempo o τ γ REVIISIÓN 3 – 75988.65 Modelos reológicos Un modelo reológico es una expresión matemática empírica que relaciona el esfuerzo cortante con la rapidez de deformación. En este sentido, la ley de Newton de la viscosidad es el modelo reológico más simple. Modelo de Bingham Como su nombre lo indica, es el adecuado para describir el comportamiento de plásticos de Bingham. Tiene dos parámetros: el esfuerzo de cedencia ( τ0 ) y una viscosidad plástica ( μ 0 ). η μ0 τ μ 0 γ τ0 τ0 γ si τ τ0 si τ τ0 η γ 0 Para la primera ecuación, se toma el signo positivo si τ 0 y el signo negativo si τ 0 . Modelo de Ostwald – de Waele (ley de la potencia) Este modelo sirve para el comportamiento de fluidos pseudoplásticos y dilatantes. Tiene dos parámetros, conocidos como índice de consistencia de flujo ( K ) y un índice de comportamiento de flujo ( n ). τ K γ n1 γ η K γ n1 Cuando n 1 el modelo predice un comportamiento pseudoplástico, y cuando n 1 da un comportamiento dilatante. Cuando n 1 , el modelo se reduce a la ley de Newton de la viscosidad con μ K . Modelo de Carreau Este modelo representa un fluido que a baja velocidad de deformación sigue la ley de Newton de la viscosidad, y a alta velocidad de deformación obedece la ley de la potencia. n1 2 τ yx μ μ 0 μ 1 λγ 2 γ 2 η μ μ 0 μ 1 λγ n1 2 donde μ 0 es la viscosidad aparente a baja velocidad de deformación (Pa·s), μ es la viscosidad aparente a alta velocidad de deformación (Pa·s), λ es un tiempo de relajación (s), y n es un índice de comportamiento. Modelo de Maxwell Éste es el modelo lineal más simple que describe el comportamiento de un fluido viscoelástico. τ λ1 τ η0 γ t donde λ 1 es una constante llamada tiempo de relajación y η0 de llama viscosidad a cero rapidez de deformación. Cuando el tensor de esfuerzo cambia muy lentamente, se puede ignorar el segundo término del lado izquierdo, y el fluido se comporta como newtoniano. Por otro lado, si el esfuerzo cambia muy rápidamente, se puede ignorar el primer término, integrar la ecuación, y se tiene una ecuación para un sólido elástico (modelo de Hooke). REVISIÓN 3 – 75988.65