Colegio Antonino 1 Taller de Repaso Anual

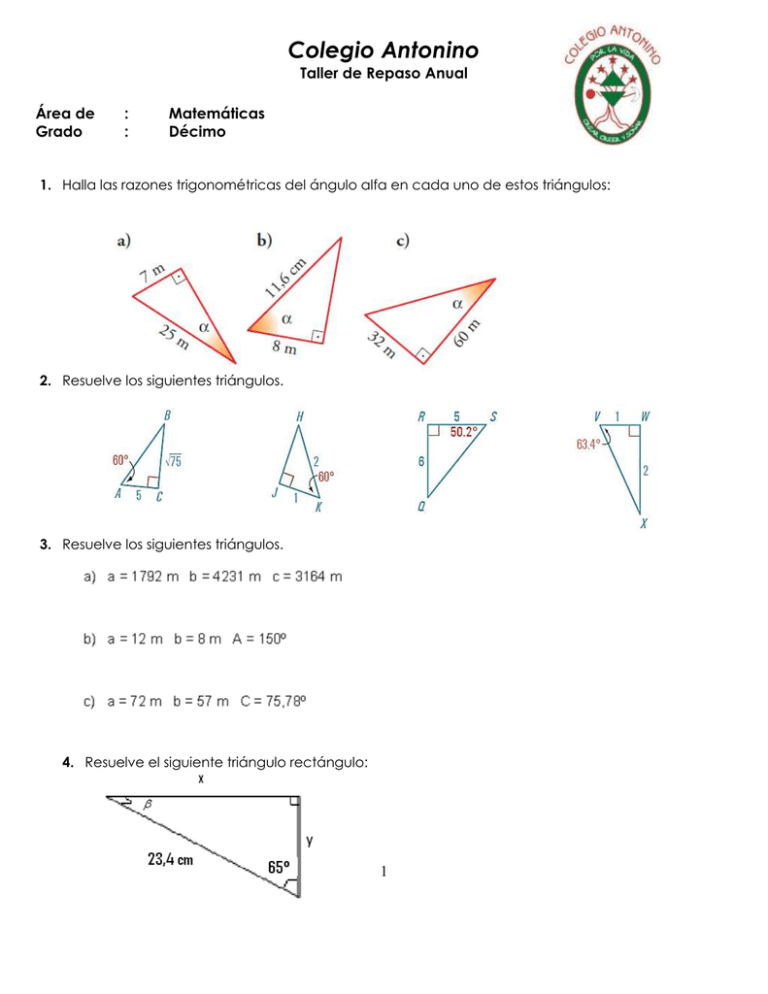
Colegio Antonino
Taller de Repaso Anual
Área de
Grado
:
:
Matemáticas
Décimo
1. Halla las razones trigonométricas del ángulo alfa en cada uno de estos triángulos:
2. Resuelve los siguientes triángulos.
3. Resuelve los siguientes triángulos.
4. Resuelve el siguiente triángulo rectángulo:
1
5. Un observador de aves encuentra un nido de alcatraces, en un punto del acantilado. ¿Qué
distancia hay entre la cima del acantilado y el nido?
6. Resuelve el triángulo de datos: A = 30°, a = 3 m y b = 8 m, y halla su área.
7. Resuelve el triángulo de datos: a = 3 m, b = 8 m y k=11,5m, y halla su área.
8. Las puntas de las ramas de un compás están separadas 9 cm y cada rama tiene 14 cm. Halla el
ángulo que forman las ramas del compás.
9. Dos barcos A y B parten del mismo embarcadero y avanzan 6 y 8 millas náuticas
respectivamente,
Si las trayectorias forman un ángulo de 60º entre si, cuál es la distancia que separaba a los
barcos al momento de partir.
10. Una escalera de 3.5 m de largo está recostada contra un muro vertical, con su extremo superior
en el muro a 2.5 metros del piso. Una señorita de 1.8 metros de estatura camina,
desprevenidamente por la acera donde está la escalera, manteniendo una distancia de 1.5 m
de separación del muro. La señorita no puede pasar por debajo de la escalera sin golpearse.
¿Cuál debe ser la estatura máxima de una persona, que camine a la misma distancia del muro
que la señorita, para pasar por debajo de la escalera sin golpearse?
11. ¿Cuántos metros cuadrados es mayor el área del triángulo BDE que el triángulo ABE?
2
12. Grafica
a. f ( x )  2sen(3x )
b.
c.
f ( x)  2 cot(2 x)
e. f ( x)  3 sec(0,5x)
f. f ( x )  4 csc(2 x )
d.
f ( x)  3 cos(x / 2)
f ( x)  1,5 tan(x)
g.
h.
f ( x)  2sen 1 ( x)
f ( x)  2 tan1 (3x)
13. Un barco navega 400 Km entre las ciudades A y B, con rumbo N65ºO. Desde la ciudad B se
dirige a otra ciudad C con rumbo N30ºE distante 250 Km; según la figura.
Calcula la distancia entre las ciudades A y C, y la dirección que
debe tomar el barco si el regreso lo hace directo entre las dos
ciudades.
Este ejercicio debe hacerse por dos métodos: la ley de cosenos y
por vectores.
14. Resuelve las siguientes ecuaciones trigonométricas:
15. Grafique la siguiente ecuación:
 3 7y
19 x

 3 x  5 
 4y
14
8
3
3
16. Demuestra las siguientes identidades:
9)
17. Halle la ecuación de una recta paralela y otra perpendicular a la recta de la figura.
18. Una recta pasa por el punto donde la recta 5x  2 y  10  0 , corta el eje Xy por el punto donde
la recta 3x  2 y  12 , corta al eje Y. Halla la ecuación de dicha recta.
19. Dados los puntos A(-4;-3), B(-3;5), C(4;4) y D(3;-4).
a. Diga cómo son los segmentos BC y AD, en cuanto a medida y relaciones entre “rectas”.
b. Halle el área y el perímetro del triángulo formado por el punto medio del segmento CD y los
puntos A y B.
 7
 2
c. Halle la distancia de un punto F  0;  , al segmento AD y al segmento BC.
4
2
2
20. Dada la ecuación 25x  16y  400, de una elipse, encuentra centro, vértices, focos, extremos
del eje menor, LEM, lem, DF y excentricidad y bosqueja la elipse.
21. Halla la ecuación general de una circunferencia que pasa por el punto A(2;-4), su centro está
ubicado en el tercer cuadrante del plano cartesiano a 3 unidades a la izquierda del punto A.
22. Halla ecuación general de una elipse con centro en O(-1;2), un vértice V1(-1;5) y un foco f1(1;2+√5). Además dibuja la elipse.
23. Halla la ecuación general de una hipérbola con centro en O(-4;1), semieje conjugado igual a 4
y distancia focal igual a 4√13. El eje transverso de esta hipérbola es paralelo al eje x.
24. Dada la ecuación de la parábola 4x 2  48y  12x  153, halle vértice, foco y ecuación de la
directriz.
25. Determina el centro, vértices, extremos del eje menor, focos, LEM, lem, DF y excentricidad de
una elipse cuya ecuación es 9 y 2  4x 2  24x  36y  36  0 . Además dibuja la elipse.
26. Determina el centro y el radio de una circunferencia cuya ecuación es: x 2  y 2  6 x  2 y  39  0
.
27. Halla la ecuación de una hipérbola cuya distancia focal es 6 y uno de sus vértices está en el
punto V1(0;-2).
28. Halla
el
centro,
focos
y
vértices
de
una
hipérbola
que
tiene
por
ecuación:
9x  4 y  54x  8 y  113  0
2
2
5 9
2 2
El foco de una parábola está en  ;  , y la ecuación de su directriz es y 
3
. Halla la
2
ecuación de dicha parábola.
29. Comprueba:
a. cosec - sen = cotg cos
d. (sen + cosec)2 = sen2 + cotg2 + 3
1  cos 
= cosec - cotg
1  cos 
e.
sen
1  cos

 2 cos ec
1  cos
sen
c. (sen + cos)2 + (sen - cos)2 = 2
f.
cos ec
 cos
cot g  tg 
b.
5
g. cos4 - sen4 +1= 2 cos2
h. sec4 - sec2 = tg4 - tg2
i.
j.
tg 2 
1  tg 2 
= sen
(sec + cos) (sec - cos) = tg2 + sen2
k. cotg4 + cotg2 = cosec4 + cosec2
l.
(1+ tg2) cos2 = 1
m. sen2 + sen2 tg2 = tg2
n. sec2 + cosec2 = sec2 cosec2
o. tg + cotg = sec cosec
p. (1 + cotg2) sen2 = 1
q. cos4 - sen4 - 2 cos2= -1
r.
sen3 cos + cos3 sen = sen cos
s.
sen 
1  cos 

 2 cos ec
1  cos 
sen 
t.
cot g 
u.
sen
 cos ec
1  cos
(1  sen )(1  sen ) =
1
sec 
v. sen2 cos2 + cos4 = cos2
w.
cos
sen

 sen  cos
1  tg  1  c tg 
6
30. La siguiente tabla muestra los coeficientes de inteligencia de 480 niños de una
escuela elemental.
C.I
.
ni
70 74 78 82 86 90 94 98 10
2
4 9 16 28 45 66 85 72 54
10
6
38
11
0
27
11
4
18
11
8
11
12
2
5
12
6
2
Calcula:
a) El C.I. medio de los niños estudiados
b) Su desviación típica.
c) Si una madre afirma que exactamente la mitad de los niños del colegio tienen un
C.I. superior al de su hijo, ¿qué C.I. tiene el niño?
d) Supongamos que se quieren hacer estudios sobre el proceso de aprendizaje de
los niños con mayor C.I., pero que el psicólogo solo puede atender al 15% de los
niños del centro. ¿Qué C.I. deberá tener un niño como mínimo para ser
considerado dentro de ese grupo de elegidos?
e) Se van a preparar unas clases de apoyo, para un 25% de los niños del centro,
precisamente para aquellos que tengan menor C.I. ¿Hasta qué niños de qué C.I.
deberemos considerar en estas clases?
31. En el siguiente histograma se representa la distribución de los salarios (variable X), en
miles de pesetas de una industria del sector cerámico:
Frecuencias relativas
0.25
0.2
0.15
0.1
0.05
0
60
80
100
120
140
160
180
200
220
240
260
Variable X (marcas de clase)
Conforme a esta información determina:
a) Tabla estadística de frecuencias
b) Salario mediano, moda.
c) Sueldo mínimo del 20% de los empleados con mayor sueldo. ¿Qué porcentaje de
la nómina corresponde a este grupo.
d) De los sueldos de otra empresa también perteneciente al sector cerámico se
sabe que el sueldo medio de sus trabajadores es de 120.000 ptas., con una
varianza de 0,5 y que la mediana de los sueldos es de 125.000 ptas. ¿Qué
empresa tiene un sueldo medio más representativo? Razona la respuesta.