Agrupación con espaciado no uniforme
Anuncio

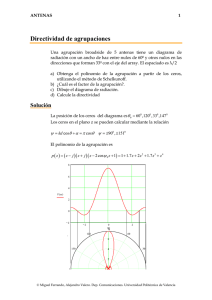
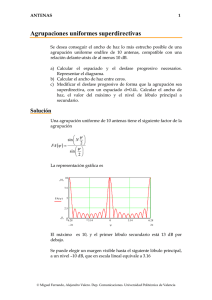
ANTENAS 1 Agrupación con espaciado no uniforme Una agrupación de 4 antenas, con igual amplitud y fase, que se pueden considerar como radiadores isotrópicos, tiene un espaciado no uniforme, tal y como se indica en la figura. a) b) c) d) Obtenga el polinomio de la agrupación Calcule los ceros del polinomio Represente el factor de la agrupación Dibuje el diagrama de radiación. 2λ λ/2 Solución La agrupación indicada se puede analizar como 2 agrupaciones de 2 elementos cada una, agrupadas a su vez El polinomio es 90 120 p ( z ) = 1 + z + 0z 2 + 0z3 + z 4 + z5 60 0.8 p ( z ) = (1 + z ) (1 + z 4 ) 0.6 150 30 0.4 0.2 El factor de la agrupación es Ψ ⎞⎛ 4Ψ z ⎞ ⎛ FA ( Ψ ) = ⎜ cos z ⎟ ⎜ cos ⎟ 2 ⎠⎝ 2 ⎠ ⎝ z = e jΨ z 180 0 0 210 330 240 300 270 El factor de la agrupación se puede calcular como el producto de dos agrupaciones uniformes, con un factor de escala en el margen visible © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 2 2 2 1.5 2cos⎛⎜ ⎝ ⎞ ⎠ ψ 2 1 2cos( 2ψ ) 0.5 0 0 3.14 2.36 1.57 0.79 −π 4 0 0.79 1.57 2.36 ψ 3.14 π 4 3 FA( ψ ) 2 1 0 0 3.14 2.36 1.57 0.79 −π 0 0.79 1.57 ψ 2.36 3.14 π El diagrama de radiación resultante es 90 120 1 60 0.8 0.6 150 30 0.4 f(θ) 0.2 180 0 0 210 0 330 240 300 270 θ El nivel de lóbulo principal a secundario es NLPS ≈ 4 4 = = 3dB ⎛π ⎞ 2 2 FA ⎜ ⎟ ⎝2⎠ © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia