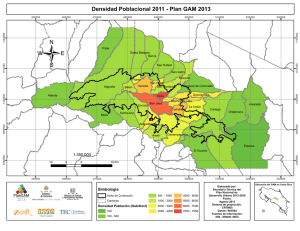
(método directo) | Age
Anuncio

ANEXO B ANNEX B B.1. Ajuste de tasas por edad (método directo) y comparaciones entre provincias B.1. Age-adjusted rates (direct method) and interprovincial comparisons El ajuste de tasas permite eliminar el componente de composición por grupos de edad de la población en la comparación de dos tasas. Para ello trata de responder a la pregunta: si las dos poblaciones tuviesen una composición etaria igual ¿cuál tendría una mortalidad mayor? El método consiste en aplicar las tasas específicas de mortalidad en la población estudiada a una población hipotética denominada población estándar. Siendo Nj las personas-año del denominador, Dj el número de defunciones, T j = Dj/Nj la tasa de mortalidad en cada grupo de edad j, y wj la proporción de individuos en el grupo de edad j (o «peso») en la población estándar. La tasa ajustada se define como la media ponderada de las tasas específicas por edad, es decir Rate adjustment makes it possible to eliminate the age-group component in the composition of two populations when comparing their respective rates. The question to be answered is: «If the two populations had identical age compositions, which would have the greater mortality?» The method consists in applying the age-specific mortality rates for the study population to a hypothetical population, denominated the standard population. Where Nj are the person-years of the denominator, Dj the number of deaths, Tj = Dj/Nj the mortality rate for each age group j, and wj the proportion of individuals in age group j (or «weight») in the standard population, the age-adjusted rate is defined as the weighted average of the age-specific rates, namely T = ∑ wjTj T = ∑ wjTj En la tabla B-1 se muestran las composiciones de las poblaciones estándar utilizadas. Cuando se trabaja con datos de mortalidad a nivel de todo el estado los problemas derivados de la estabilidad estadística de las tasas tienen poca importancia en general. Sin embargo, en los niveles provinciales y en enfermedades raras las tasas pueden estar basadas en pocos casos; por ello, el cálculo del error estándar de las tasas pueden ser de Table B-1 shows the compositions of the standard populations used. When working with mortality data at a national level, problems arising out of the statistical stability of the rates are of little importance in general. However at provincial levels and in rare diseases, rates may be based on relatively few cases; in such instances, calculation of the standard error of the rates may then be of interest. Where 323 Atlas de mortalidad por cáncer en España interés. Si las defunciones en el numerador de las tasas específicas siguen una distribución de Poisson, su varianza es Var(Dj) = NjTj, que puede ser estimada por Dj, pudiéndose considerar las personas-año como una constante. En ese caso, la varianza de una tasa específica Tj se estima como Dj/Nj2, el cuadrado de la constante «1/Nj» multiplicado por la varianza de la variable aleatoria «Dj» (11). deaths in the specific-rate numerator follow a Poisson distribution, variance is Var(Dj) = NjTj, which can be estimated by dj, with person-years being regarded as a constant. In this case, the variance of a specific rate Tj is estimated as Dj/Nj2, the square of the constant «1/Nj» multiplied by the variance of the random variable «Dj» (11). El error estándar de la tasa ajustada es: The standard error of the adjusted rate is: EE(T) = (∑ wj2 Dj/Nj2)1/2 EE(T) = (∑ wj2 Dj/Nj2)1/2 El error estándar de las tasas ajustadas puede ser utilizado para valorar la significación estadística de la diferencia entre tasas de dos provincias, mediante la aproximación de la distribución de Poisson a una normal. Por ejemplo, si la tasa de una provincia es T1 y de otra es T2 y sus errores estándar S1 y S2, podemos calcular χ = (T1 – T2)/√(S12+ S22) y si χ > 1,96 las diferencias son estadísticamente significativas (19). También puede calcularse fácilmente una aproximación al intervalo de confianza de la razón de tasas ajustadas utilizando la propuesta de Miettinen (T1/T2)1 ± Zα/2/χ siendo χ el calculado anteriormente y Ζα/2 = 1,96 para los límites de confianza al 95% (20). Hay que tener en cuenta que este tipo de comparaciones ignora la presencia de interacciones entre la provincia y la edad, es decir, asume que el riesgo es homogéneo por estratos de edad. The standard error of the adjusted rates may be used to assess the statistical significance of the difference in rates between two provinces, by means of approximation of the Poisson to a normal distribution. For example, if the rate for one of the provinces is T1 and that of the other T2, and their standard errors S1 and S2, one can calculate χ = (T1 – T2)/√(S21+ S22); and if χ > 1.96, then the differences are statistically significant (19). Similarly, an approximation to the confidence interval of the adjusted rate ratios may be easily computed by following the method proposed by Miettinen (T1/T2)1 ± Zα/2/χ, where the value of χ is as calculated above and Ζα/2 = 1.96 for 95% confidence limits (20). One has to bear in mind that these types of comparisons ignore the presence of interactions between province and age, that is to say, risk is assumed to be homogeneous across any given age stratum. B.2. Tasa acumulada y riesgo acumulado B.2. Cumulative rate and cumulative risk Se ha propuesto el cálculo de la tasa acumulada como medida de estandarización directa en el contexto de la epidemiología del cáncer (19). Esta medida presenta las ventajas de obviar la arbitrariedad en la selección The calculation of the cumulative rate has been suggested as a measure of direct standardization in the context of cancer epidemiology (19). This measure possesses the dual advantage of avoiding arbitrariness in 324 Anexo B de la población estándar y de que los cálculos son más simples. Sin embargo, su utilidad principal se deriva de ser una aproximación habitualmente muy buena al riesgo acumulado, que es el indicador presentado en las tablas (columna RACU). El riesgo acumulado es el riesgo de que un individuo desarrolle y muera de una enfermedad durante un período de tiempo si no existiesen otras causas de muerte. Normalmente como período de tiempo se considera la edad desde 0 a 74 años. Siendo I(t) la tasa de incidencia instantánea a una edad, el riesgo acumulado entre las edades t 1 y t 2 es ( ∫t 1 – exp – the selection of the standard population and requiring far simpler calculations. Nevertheless, its chief utility resides in its normally being an extremely good approximation to cumulative risk, the indicator presented in the tables (RACU column). Cumulative risk is the risk of an individual developing and dying of a disease during a period of time provided that no other causes of death exist. Normally, the period of time is taken as the age-span from 0 to 74 years. Where I(t) denotes the instantaneous incidence rate at any given age, the cumulative risk between ages t 1 and t2 is ( ∫t t2 I(t)dt ) 1 1 – exp – 15 In our case, this expression is calculated as follows ) ( 1 – exp – ∑ 5Tj j=1 ) 1 Esta expresión en nuestro caso se aproxima como ( t2 I(t)dt 15 ) 1 – exp – ∑ 5Tj j=1 por utilizar intervalos de edad de 5 años y ser el cálculo hasta los 74 años de edad, excluyendo el grupo de 75 y más. Hemos expresado el riesgo acumulado en forma de porcentaje, lo cual tiene la ventaja de tener una interpretación muy intuitiva y es comparable entre provincias por ser una medida estandarizada. This is due to 5-year age intervals being used and the calculation being taken up to the 74-year mark (excluding the 75-andover group). Cumulative risk has been expressed in the form of a percentage, which enjoys the advantage of being open to highly intuitive interpretation, as well as being a standardized yardstick allowing for interprovincial comparisons. B.3. Cálculo de tasas de mortalidad ajustadas por edad, errores estándar, tasa truncada ajustada y riesgo acumulado. Comparaciones entre provincias B.3. Calculation of age-adjusted mortality rates, standard errors, truncated adjusted rate and cumulative risk. Interprovincial comparisons. Describimos en detalle el cálculo de las tasas ajustadas, sus errores estándar, el riesgo acumulado y la comparación de tasas ajustadas entre provincias. Para ello utilizamos los datos del atlas referidos al cáncer de A detailed description now follows of the computation of adjusted rates, their standard errors, cumulative risk and interprovincial comparisons of adjusted rates. For this purpose, use had been made of atlas data on 325 Atlas de mortalidad por cáncer en España páncreas en las provincias de Las Palmas y Santa Cruz de Tenerife. Para los cálculos explicados a continuación las tasas específicas han de ser divididas por 100.000. cancer of the pancreas in Las Palmas and Santa Cruz de Tenerife provinces. For the calculations explained below, specific rates have to be divided by 100,000. En la tabla B-2 se muestran todos los pasos de los cálculos. En primer lugar se calculan las tasas específicas por edad que son multiplicadas por la población estándar. Con esto se obtienen los casos esperados en esta población estándar (si tuviese la misma mortalidad que la población estudiada) que sumamos al final de la columna. La población estándar suma 100.000 con lo que el indicador que obtenemos es la tasa ajustada por 100.000. Para el cálculo de las tasas específicas el denominador se construye multiplicando la población a mitad de período por el tiempo a riesgo (en nuestro estudio 15 años). Table B-2 sets out all the various steps of the calculations. In the first place, age-specific rates are reckoned and multiplied by the standard population. This gives the number of expected cases in the standard population (provided of course that this reports the same mortality as the study population), said cases being summed and shown at the bottom of the column. The standard population totals 100,000 so that the indicator obtained is the rate adjusted by 100,000. In order to calculate specific rates, the denominator is arrived at by multiplying the midpoint population by the time at risk (in our study, 15 years). El mismo procedimiento se sigue para la tasa truncada ajustada, que en este caso es entre 35 y 64 años de edad. Para ello se ponderan como 0 los grupos de edad no comprendidos entre 35 y 64. The same procedure is followed for the truncated adjusted rate, which in this case is between 35 and 64 years of age. Here a weighting of 0 is accorded to age groups not falling within the 35-64 range. Con este mismo procedimiento también calculamos la tasa acumulada, en la que los pesos corresponden a la longitud del intervalo de edad, es decir, 5 años. Para convertir la tasa acumulada en el riesgo acumulado (RACU) utilizamos la expresión «1 – exp(– tacu)». Para expresarlo en porcentaje lo multiplicamos por 100. This method is again used to obtain the cumulative rate (RACU), in which the weights correspond to the length of the age interval, viz., 5 years. To convert the cumulative rate into cumulative risk (CUR), recourse is had to the expression «1 – exp(– tacu)». This is then multiplied by 100 in order to express it as a percentage. La varianza de una tasa específica es D/N2. Para calcular el error estándar de la tasa ajustada multiplicamos la varianza de cada tasa específica por el cuadrado de la población estándar (wj). Sumamos el total de la columna y hacemos la raíz cuadrada. The variance of a specific rate is D/N2. To calculate the standard error of the adjusted rate, the variance of each specific rate is multiplied by the square of the standard population (w j). The column is summed and the square root of the total ascertained. Para la comparación de las tasas ajustadas For comparison of adjusted rates χ = (11,96-8,21)/(0,343+0,221)1/2 = 4,99 (P<0,01) χ = (11.96-8.21)/(0.343+0.221)1/2 = 4.99 (P<0.01) Para el cálculo de la razón de tasas y su intervalo de confianza To calculate the rate ratio and its confidence interval RR = T 1/T2= 11,96/8,21 = 1,46 RR = T 1/T2= 11.96/8.21 = 1.46 326 Anexo B 1,46(1 ± 1,96/4,99) límite inferior 1,26 1.46(1 ± 1.96/4.99) límite superior 1,69 Con estos resultados se puede afirmar que en el período de estudio Las Palmas ha tenido un 46% más de mortalidad por cáncer de páncreas en hombres, siendo la estimación de la razón de tasas 1,46 (intervalo de confianza al 95% 1,26-1,69). 1.46(1 ± 1.96/4.99) lower limit 1.26 1.46(1 ± 1.96/4.99) lower limit 1.69 On the basis of these results one can conclude that during the study period, there was a 46% greater mortality rate for cancer of the pancreas among men in Las Palmas, the rate ratio being estimated at 1.46 (95% CI 1.26-1.69). Tabla B-1. Composición de las poblaciones estándar o pesos utilizados. Table B-1. Composition of standard populations and weights used. Grupo edad Poblac. mundial Poblac. europea Truncada europea Tiempo APVP Age group World population Europ. population Europ. truncated Time PYLL 051015202530354045505560657075- 12000 1000 9000 9000 8000 8000 6000 6000 6000 6000 5000 4000 4000 3000 2000 2000 8000 7000 7000 7000 7000 7000 7000 7000 7000 7000 7000 6000 5000 4000 3000 4000 0 0 0 0 0 0 0 19350 19350 19350 16130 12910 12910 0 0 0 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 0 0 0 0 0 43,5 38,5 33,5 28,5 23,5 18,5 13,5 8,5 3,5 0 0 0 327 Atlas de mortalidad por cáncer en España Tabla B-2. Cálculo de tasas de mortalidad ajustadas por edad, errores estándar, tasa truncada ajustada y riesgo acumulado. Comparaciones entre provincias. Table B-2. Calculation of age-adjusted mortality rates, standard errors, truncated adjusted rate and cumulative risk. Interprovincial comparisons. Las Palmas de Gran Canaria Grupo edad j Defunciones Dj Población Nj Tasa específica Tj Poblac. estandar wj Casos esperados wjTj Var(Tj) x w2j Población e. trun vj Casos esperados vjTj Tiempo t Tj x t Age group j Deaths Dj Population Nj Age Spec. rate Tj Std. pop. wj Expected cases wjTj Var(Tj) x w2j Europ. trun. pop vjMj Expected cases vjTj Time t Tj x t 0051015202530354045505560657075- 0 0 0 0 0 1 0 1 4 8 17 31 53 52 79 66 109 8000 8000 7000 7000 7000 7000 7000 7000 7000 7000 7000 7000 6000 5000 4000 3000 4000 0,00000 0,00000 0,00000 0,00000 0,00000 0,01266 0,00000 0,01782 0,08177 0,17575 0,38586 0,78114 1,47151 1,59504 2,26280 1,71629 3,45620 0,00000 0,00000 0,00000 0,00000 0,00000 0,00016 0,00000 0,00032 0,00167 0,00386 0,00876 0,01968 0,04086 0,04893 0,06481 0,04463 0,10959 0,00000 0,00000 0,00000 0,00000 0,00000 0,00000 0,00000 0,00000 0,22605 0,48583 1,06663 1,79996 3,16619 4,11840 0,00000 0,00000 0,00000 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 0 0,0000000 0,0000000 0,0000000 0,0000000 0,0000000 0,0000090 0,0000000 0,0000127 0,0000584 0,0001255 0,0002756 0,0005580 0,0012263 0,0015950 0,0028285 0,0028605 0,0000000 Total 421 11,95680 0,34327 27231 30130 36783 41006 41062 36866 30959 26189 22827 21242 20560 18520 14407 10867 9310 7691 8410 0,0000 0,0000 0,0000 0,0000 0,0000 0,1808 0,0000 0,2546 1,1682 2,5107 5,5123 11,1591 24,5251 31,9009 56,5700 57,2097 86,4051 0 0 0 0 0 0 0 0 19350 19350 19350 16130 12910 12910 0 0 0 10,86310 0,0094591 Santa Cruz de Tenerife Grupo edad j Defunciones Dj Población Nj Tasa específica Tj Poblac. estandar wj Casos esperados wjTj Var(Tj) x w2j Población e. trun vj Casos esperados vjTj Tiempo t Tj x t Age group j Deaths Dj Population Nj Age Spec. rate Tj Std. pop. wj Expected cases wjTj Var(Tj) x w2j Europ. trun. pop vjMj Expected cases vjTj Time t Tj x t 8000 7000 7000 7000 7000 7000 7000 7000 7000 7000 7000 6000 5000 4000 3000 4000 0,00000 0,00000 0,00000 0,00000 0,00000 0,01767 0,00000 0,02206 0,14603 0,18905 0,59116 0,84258 1,30242 1,24961 1,46602 2,37993 8,20650 0,00000 0,00000 0,00000 0,00000 0,00000 0,00031 0,00000 0,00049 0,00355 0,00447 0,01588 0,02366 0,03688 0,03123 0,03643 0,06824 0,22115 051015202530354045505560657075Total 0 0 0 0 0 1 0 1 6 8 22 30 46 50 59 83 306 27231 33153 35381 35154 30335 26411 23119 21151 19174 19748 17367 14242 11773 10670 8049 9300 0,0000 0,0000 0,0000 0,0000 0,0000 0,2524 0,0000 0,3152 2,0862 2,7007 8,4451 14,0430 26,0483 31,2402 48,8674 59,4982 0 0 0 0 0 0 0 19350 19350 19350 16130 12910 12910 0 0 0 0,00000 0,00000 0,00000 0,00000 0,00000 0,00000 0,00000 0,06099 0,40367 0,52258 1,36220 1,81295 3,36284 0,00000 0,00000 0,00000 7,52520 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 0 0,0000000 0,0000000 0,0000000 0,0000000 0,0000000 0,0000126 0,0000000 0,0000158 0,0001043 0,0001350 0,0004223 0,0007021 0,0013024 0,0015620 0,0024434 0,0000000 0,0066550 Las tasas específicas «T j» están expresadas en casos por 100.000 personas-año. / Age-specific rates «T j» are expressed in cases por 100,000 person-year. 328