Jorge Fallas - Sistema de Información de Recursos Forestales

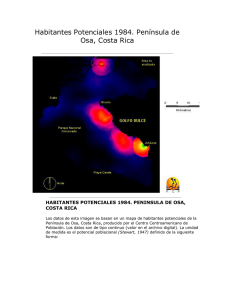
Evaluación del error esperado al configurar los receptores
Garmin para trabajar con las cuadrículas Lambert Norte y Sur
de Costa Rica
Jorge Fallas
Laboratorio de Teledetección y Sistemas de Información Geográfica
PRMVS-EDECA, UNIVERSIDAD NACIONAL
2003
Indice
Introducción ...................................................................................................................1
Metodología ...................................................................................................................1
Evaluación del error de cada una de las configuraciones .................................................2
Resultados y discusión....................................................................................................3
El Sistema CRTM (Costa Rica Transversal de Mercator)................................................7
Conclusiones ..................................................................................................................9
Referencias.....................................................................................................................9
1
Introducción
La mayoría de los receptores de bajo costo (US$100 a 300) del Sistema de Posicionamiento
Global (conocidos como GPS por sus siglas en Inglés) tienen un error de posicionamiento de
10 a 15 m. Los nuevos receptores con capacidad de recibir señales WAAS (Wide Area
Augmentation System) pueden reducir dicho error a 5m. Sin embargo, si el receptor no se
configura y utiliza correctamente la posición registrada por el usuario (a) en el sistema local
de referencia puede tener un error de varios cientos de metros. La mayor parte de los usuarios
desean utilizar el receptor en conjunto con la cartografía nacional; sin embargo estos
receptores no cuentan con una configuración compatible con la cuadrícula Lambert Norte y
Sur utilizada en Costa Rica. En un documento previo (Fallas, 2003) el autor trató el tema de la
conversión del datum WGS84 a Ocotepeque utilizando una extensión para ArcView 3.x. Esta
es una alternativa para aquellos usuarios(as) que poseen el programa y que además requieran
de una solución rigurosa; sin embargo no resuelve el problema de quienes desean leer
directamente del receptor valores compatibles con las cuadrículas Lambert de Costa Rica. Con
el fin de proponer una configuración compatible con las cuadrículas Lambert, en el presente
documento se evalúa el error esperado para la configuración de una cuadrícula UTM del
usuario sugerida inicialmente por Henry Chaves (hchaves@una.ac.cr ,TELESIG-UNA) y
Jorge Benavidez (jbenavidez@cruzroja.or.cr).
Metodología
El estudio se realizó utilizando 28 puntos de posición conocida en Lambert Norte, Sur y
CRTM (Dörries y Roldán, 1999); su distribución a nivel nacional es adecuada con la
excepción del flanco sureste de la Cordillera de Talamanca y una porción en la Zona Norte
(Figura 1).
Figura 1: Puntos de referencia utilizados en la evaluación del error radial esperado al utilizar
una cuadrícula UTM del usuario con las cuadrículas Lambert de Costa Rica.
2
Las cuadrículas UTM del usuario se configuraron de la siguiente manera:
Lambert Norte
Parámetro
HCHAVES*
JFALLAS**
Longitud de origen
84º 20.000'
84º 20.000'
Factor escala
0.99996
0.99996
Falso este
499800
499800
Falso norte
-885250
-885244
Datum
NAD 27 América Central
Lambert Sur
Parámetro
HCHAVES*
JFALLAS**
Longitud de origen
83º 40.000'
83º 40.000'
Factor escala
0.99996
0.99996
Falso este
499800
499800
Falso norte
-667115
-666875
Datum
NAD 27 América Central
* Configuración original sugerida por Henry Chaves y Jorge Benavides
** Configuración final sugerida por el autor
Evaluación del error de cada una de las configuraciones
1. A partir de los puntos de posición conocida en latitud-longitud y con datum WGS84
(Dörries y Roldán 1999) se creó un tema de puntos en ArcView (www.esri.com).
Luego, utilizando la extensión DNRGarmin (Pouliot y Loesch, 2003) dichos puntos
fueron trasladados a un receptor Garmin MAP76s (www.garmin.com).
2. Utilizando el menú del receptor se configuró en la sección de “Localización” una
parrilla o cuadrícula UTM del usuario con los siguientes parámetros:
Caso 1: Para operar con la cuadrícula Lambert Norte
Origen de longitud: 84º 20.000'
Escala: 0.99996
Falso Este: 499800
Falso Norte: -885244
Datos de mapa (datum): NAD27 Central
Caso 2: Para operar con la cuadrícula Lambert Sur
Origen de longitud: 84º 40.000'
Escala: 0.99996
Falso Este: 499800
Falso Norte: -666875
Datos de mapa (datum): NAD27 Central
3. El error planimétrico se calculó como el desplazamiento radial (Figura 2) entre la
posición de cada uno de los puntos en Lambert Norte ó Sur, Ocotepeque y la posición
leída desde el receptor de GPS utilizando la respectiva Parrilla UTM del usuario
(Acharya y Bell, 1992; Giovachino, 1992).
3
Figura 2 : Estimación del error radial. En este caso el error radial es igual a ((10)2 + (10)2)0.5,
lo que equivale a 14.1m
4. El error medio en posicionamiento (raíz del error medio cuadrático) para cada una de
las configuraciones se calculó como:
REMC= [ ? (Exy)2 / n ] 0.5; en donde: Exy es igual al error radial o total en posicionamiento
y “n” el número de puntos evaluados.
Resultados y discusión
La proyección conformal cónica de Lambert está basada en un cono secante que corta el
esferoide en dos paralelos estándares o normales. Dichos paralelos se escogen de tal forma
que dos terceras partes del ámbito norte-sur de la proyección se encuentran entre ellos, un
sexto se encuentre al norte del paralelo estándar superior y un sexto al sur del paralelo
estándar inferior. En esta proyección los meridianos (longitud) son líneas rectas y los
paralelos (latitud) son arcos concéntricos. La proyección puede extenderse en el sentido esteoeste pero no en la dirección norte-sur sin incurrir en fuertes errores. La distorsión en la escala
depende solo de la latitud y por tanto esta proyección es apropiada para áreas que se extienden
en dirección este-oeste. Las coordenadas X,Y son medidas en metros. El falso este y el falso
norte representan coordenadas X y Y respectivamente seleccionadas de tal forma que no
existan valores negativos en la cuadrícula. Para minimizar las distorsiones de la proyección,
las cuales aumentan conforme nos alejamos del paralelo estándar, el país fue dividido en dos
cuadrículas LAMBERT Norte y LAMBERT Sur. Los parámetros de la proyección
LAMBERT de Costa Rica son los siguientes (Inter-American Geodetic Survey, 1950):
CUADRÍCULA LAMBERT NORTE
Latitud del primer paralelo estándar (paralelo sur) : 9° 56' N (9.933334)
Latitud del segundo paralelo estándar (paralelo norte): 11° 00' N (11.00000)
Longitud del meridiano central o de origen (eje X): 84° 20 ' W (-84.333334)
Latitud de origen de la proyección (eje Y): 10° 28' N (10.466667)
Falso este (eje X): 500000 metros
Falso norte (eje Y): 271820.522 metros
Constante para la cuadrícula (R0 +FN): 34800000 metros
Factor de escala en el origen: 0.99995696
4
CUADRÍCULA LAMBERT SUR
Latitud del primer paralelo estándar (paralelo sur) : 8° 28' N (8.4666667)
Latitud del segundo paralelo estándar (paralelo norte): 9° 32' N (9.533334)
Longitud del meridiano central o de origen (eje X): 83° 40 ' W (-83.666667)
Latitud de origen de la proyección (eje Y): 9° 00 ' N (9.00000)
Falso este (eje X): 500000 metros
Falso norte (eje Y): 327987.436 metros
Constante para la cuadrícula (R0 +FN): 40600000 metros
Factor de escala en el origen: 0.99995696
Figura 3: Propiedades de las cuadrículas Lambert Norte y Sur.
Ambas cuadrículas utilizan el elipsoide de Clark 1866 cuyas parámetros son:
Semieje mayor (a): 6378206.4 m
Semieje menor(b): 6356583.8 m
Factor de achatamiento: Df: (a-b)/a = 0,00339000 y 1/f = 294,978698
Factor de excentricidad : e2 = (a2-b 2)/a2 = 0,006768657997291
Las propiedades de la proyección Lambert son (ESRI, 1994):
Forma: Es conformal y por lo tanto representa con exactitud áreas pequeñas.
Área: La distorsión es mínima cerca de los paralelos estándar. La escala se reduce
entre los paralelos estándares e incrementa al alejarnos de ellos.
Dirección: Ángulos locales verdaderos.
Distancia: La escala es verdadera a lo largo de los paralelos estándares. La escala se
reduce entre los paralelos e incrementa al alejarnos de ellos.
5
Las hojas topográficas escala 1:50.000 del Instituto Geográfico Nacional están impresas
utilizando las dos cuadriculas como puede observarse en la figura 4.
Figura 4: División de las hojas 1:50.000 del IGN-CR en Lambert Norte y Sur.
La figura 5 presenta los errores radiales estimados al restar la lectura obtenida con el
receptor GPSmap 76S de Garmin de la posición verdadera de cada uno de los puntos. Para los
28 puntos, la raíz del error medio cuadrático fue de 21.8 m, con un mínimo de 0 m y un
máximo de 72 m. Sin embargo al calcular el error medio solo para los puntos ubicados en la
zona correspondiente a la cuadrícula Lambert Norte el mismo se redujo a 7.7 m (rango de 2 a
17 m). La figura 6 presenta los resultados homólogos para la cuadrícula Lambert Sur. La raíz
del error medio cuadrático fue de 47.8 m para la totalidad de los puntos (error mínimo 1 m y
máximo 124 m). Sin embargo al calcular el error para los puntos correspondientes a la
cuadricula Lambert Sur el error se redujo a 4.5m (rango 1 y 8 m). A partir de estos resultados
el usuario(a) de las cuadrículas puede esperar que en promedio un 95% de las observaciones
tengan un error de 15.1m en Lambert Norte y 8.8m en Lambert Sur. Los errores indican que
las configuraciones utilizadas para las cuadrículas UTM aproximan muy bien los valores
esperados para las cuadrículas Lambert de Costa Rica. El error obtenido es apropiado para
trabajar con escalas de hasta 1:10000 (ver cuadro1). Para trabajos que requieran un menor
error se recomienda utilizar la extensión CR_proyección_datum.avx para realizar primero la
transformación de datum (WGS84 a Ocotepeque) y luego proyectar los valores de Lat-Long a
Lambert (Fallas,2003).
6
Figura 5: Error esperado para la parrilla UTM del usuario configurada para operar con la
cuadrícula Lambert Norte. Error medio cuadrático 7.7m.
Figura 6: Error esperado para la parrilla UTM del usuario configurada para operar con la
cuadrícula Lambert Sur. Error medio cuadrático 4.5m.
7
La exactitud y precisión de un mapa o producto cartográfico (digital o papel) depende de
la escala a la cual fue compilado. El estándar utilizado por el Servicio Geológico de los
Estados Unidos de América establece que “no mas del 10% de los puntos evaluados deben
tener un error horizontal superior a 0.846 mm para mapas a escala 1:20.000 o superiores y
0.508 mm para mapas con escalas inferiores a 1:20.000”. El cuadro 1 se confeccionó
utilizando dicho estándar y puede servirle al lector(ora) como una guía para evaluar el error
obtenido con las configuraciones de las cuadriculas UTM del usuario propuestas en el
presente trabajo.
Cuadro 1: Error máximo esperado para el 90% de los puntos muestreados. Estándar del
Servicio Geológico de los Estados Unidos de América.
Escala
Error (m)
1.0
1:1200
1:2400
2.0
1:4800
4.1
1:10000
8.5
1:20000
16.9
1:25000
12.7
1:40000
20.3
1:50000
25.4
1:63600
32.2
1:75000
38.1
1:100000
50.8
1:150000
76.2
1:200000
101.6
El Sistema CRTM (Costa Rica Transversal de Mercator)
La proyección Costa Rica Transversal de Mercator utiliza un cilindro para proyectar los
elementos de la superficie terrestre. El cilindro está orientado en sentido este-oeste y la
proyección representa sin distorsión la curvatura de la Tierra en sentido norte-sur pero no en
dirección este-oeste. Este proyección es apropiada para países cuyo eje mayor se extiende en
sentido Norte-Sur. Para Costa se ha propuesto utilizar dicha proyección con los siguientes
parámetros (Figura7):
Figura 7: La proyección Costa Rica Transveral de Mercator
8
Longitud del meridiano central o de origen (eje X): 84o 00' 00 '' W (84.0000)
Latitud de origen 00 o 00' 00 '' N (0.0000)
Falso este (eje X): 500000 metros
Falso norte (eje Y): 0 metros
Factor de escala en el meridiano central: 0.9996
Los valores seleccionados para el falso este (Eje X) y falso norte (Eje Y) generan valores
positivos para la cuadrícula en todo el país. Las propiedades de esta proyección son (ESRI,
1994):
Forma: Es conformal y por lo tanto representa con exactitud áreas pequeñas. La
distorsión de áreas grandes incrementa al alejarse del meridiano central.
Área: La distorsión incrementa al alejarse del meridiano central.
Dirección: Ángulos locales verdaderos.
Distancia: La escala es constante a lo largo del meridiano central cuando el factor de
escala es 1.0. Si el factor de escala es menor que 1 (como el propuesto para Costa
Rica) entonces existen dos rectas con escalas constantes a ambos lados del meridiano
central.
La proyección CRTM utiliza el datum WGS84 (Sistema Geodésico de referencia de
1984). Esta proyección es utilizada por el Catastro Nacional, la Municipalidad de San José y
en la cartografía escala 1:25.000 del proyecto TERRA. Los parámetros del elipsoide WGS84
son:
Semieje mayor: 6378137.00 m
Semieje menor: 6356752.31 m
Factor de achatamiento: f= 0.00335281 y 1/f= 298.2571
La figura 8 presenta los errores radiales estimados al restar la lectura obtenida con el
receptor GPSmap 76S de Garmin configurado como una cuadrícula UTM de usuario y la
posición verdadera de cada uno de los puntos. Para los 28 puntos, la raíz del error medio
cuadrático fue de 0.4m, con un mínimo de 0 m y un máximo de 1.2 m. El error obtenido es
muy pequeño y apropiado para trabajar con escalas de hasta 1:2500.
9
Figura 8: Error esperado para la parrilla UTM del usuario configurada para operar con la
cuadrícula CRTM.
Conclusiones
Las configuraciones de las cuadrículas UTM de usuario utilizadas en la presente
investigación indican que los errores medios esperados tanto para la cuadrícula Lambert Norte
(7.7m) como para Lambert Sur (4.5m) son apropiados para trabajar con la cartografía
1:10.000 del Instituto Geográfico Nacional de Costa Rica. Para la configuración de CRTM el
error medio (0.4m) permite realizar trabajos con una escala de hasta 1:2500.
Referencias
Acharya, B. y Bell, W. 1992. Universal accuracy standards for a GIS. In. ASPRS/ACSM/RT
92 Technical Papers. Vol 3. GIS and Cartography. pp. 368-379. American Society for
Photogrammetry and Remote Sensing and American Congress on Surveying and Mapping.
Bethesda, MD. USA.
American Society for Photogrammetry and Remote Sensing. 1989. Interim accuracy
standards for large scale line maps. Photogrammetric Eng. and Remote Sensing. 55:10381040.
American Society for Photogrammetry and Remote Sensing (ASPRS). Specifications and
Standards Committee. 1990. ASPRS Accuracy Standards for Large-Scale Maps:
Photogrammetric Engineering and Remote Sensing, v. 56, no. 7, p. 1068-1070.
10
ANSI-NCITS, 1998. American National Standards Institute, Information Technology –
Spatial Data Transfer Standard (SDTS) (ANSI-NCITS 320:1998): New York, New York.
Barrantes Ferreo, Mario. 1966. El mapa básico de Costa Rica. Ministerio de Transportes.
Instituto Geográfico de Costa Rica. 18p.
DCDSTF.1988. The proposed standard for digital cartographic data. The American
Cartographer 15:9-140.
Dörries, Esteban y Roldán, Julio. 1999. Estudio comparativo del datum geodésico de
Ocotepeque y el datum satelitario del sistema WGS84. Informe final del proyecto de
investigación. Escuela de Topografía, Catastro y Geodesia. Facultad de Ciencias Exactas y
Naturales. Universidad Nacional. Heredia, Costa Rica. 172p.
ESRI. 1994. Map Projections. Georeferencing spatial data. Redlands, CA. USA.
Fallas, Jorge. 2003. Extensión CR_proyeccion_datum.avx. Transformación de datum y
proyección de Costa Rica utilizando ArcView GIS. Laboratorio de Teledetección y Sistemas
de Información Geográfica. Programa Regional en Manejo de Vida Silvestre-Escuela de
Ciencias Ambientales. Universidad Nacional, Heredia, Costa Rica. 10p.
Federal Geographic Data Committee. 1998a. Part 1, Reporting Methodology,
GeospatialPositioning Accuracy Standards, FGDC-STD-0007.1-1998, Washington, D.C.
http://fgdc.er.usgs.gov/fgdc.html
Federal Geographic Data Committee, Part 1, Reporting Methodology, Geospatial Positioning
Accuracy Standards, FGDC-STD-0007.1-1998, Washington, D.C., 1998.
http://fgdc.er.usgs.gov/fgdc.html
Federal Geographic Data Committee1998b. Part 3., National Standard for Spatial Data
Accuracy, Geospatial Positioning Accuracy Standards, FGDC-STD-007.3-1998: Washington,
D.C., 1998. http://fgdc.er.usgs.gov/fgdc.html
Federal Geographic Data Committee, Part 1, Reporting Methodology, Geospatial Positioning
Accuracy Standards, FGDC-STD-0007.1-1998, Washington, D.C., 1998.
http://fgdc.er.usgs.gov/fgdc.html
Giovachino, D. 1992. Graphic digitizing accuracy. In. ASPRS/ACSM/RT 92 Technical
Papers. Vol 3. GIS and Cartography. pp. 380-389. American Society for Photogrammetry and
Remote Sensing and American Congress on Surveying and Mapping. Bethesda, MD. USA.
Inter-American Geodetic Survey. 1950. Proyección Lambert para Costa Rica. Army Map
Service, Washington, D.C. USA. 25p.
Pouliot, Christopher y Loesch, Timothy.2003. “DNR_Garmin” V4.0. Departamento de
Recursos Naturales del Estado de Minnesota, USA
(http://www.dnr.state.mn.us/mis/gis/tools/arcview/)
United States National Map Accuracy Standards. 1970. US Bureau of the Budget Release
1204, Appendix, Part 800, chapter1. Versión electrónica http://fgdc.er.usgs.gov/fgdc.html