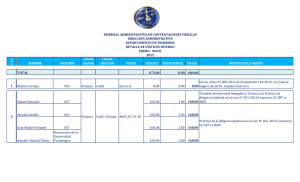
Estimación MOP y MTE mediante mínimos cuadrados

Estimación MOP y MTE mediante mínimos
cuadrados
Inmaculada Pérez Bernabé y Antonio Salmerón Cerdán (Director)
Departamento de Matemáticas
Universidad de Almería
Desarrollo del problema
Introducción
Estimación Paramétrica
Redes bayesianas
La estimación del funciones MOP y MTE por mínimos cuadrados
consiste en encontrar los valores de los parámetros ai que minimizan el error cuadrático. Se plantean dos enfoques para esta estimación paramétrica:
✔ A partir de la función de densidad f (x ).
✔ Las redes bayesianas son herramientas para la modelización de
problemas en los que intervienen un conjunto de variables y existe
incertidumbre acerca de las relaciones entre las mismas.
Cualitativa: estructura de la red.
Cuantitativa: distribuciones de probabilidad.
✔ Ventaja: es posible representar de forma eficiente una distribución
de probabilidad multivariante, en la que la propia estructura de la red
codifica las relaciones de independencia entre las variables.
P ( X1 , X2 , . . . , Xn ) =
n
Y
minimizar
k =1
sujeto a
P (Xi | pa(Xi )).
f ∗(xk ) > 0
f ∗(x )dx = #Aj (x1, . . . , xm ),
✔ A partir de la función de distribución F (X ).
m
X
1
(Gm (xk ) − F ∗(xk ))2
minimizar
m
X1
X3
sujeto a
X5
X4
Z X
n
Aj i =0
i =1
X2
m
X
1
(h (xk ) − f ∗(xk ))2
m
k =1
∗′
F (x ) > 0 ∀x ∈ Aj ,
j −1
X
#As (x1, . . . , xm )
F ∗(xmin ) =
✔ Las redes bayesianas híbridas modelan problemas en donde coF ∗(xmax ) =
existen simultáneamente variables de naturaleza discreta y continua.
s =1
j
X
#As (x1, . . . , xm ),
s =1
Objetivo general
BIC
Desarrollar esquemas de inferencia y aprendizaje en redes bayesianas híbridas basadas en modelos MTE (Moral et al., 2001) y
MOP (Shenoy y West, 2011).
Esta medida nos aporta información acerca de la bondad del modelo ajustado:
BIC (f ; bx ) =
Definiciones
m
X
k =1
✔ Nos ayuda a determinar el grado del polinomio y el número de
Función MOP unidimensional
f (x ) =
n
X
i
ai ,j x ,
N (f )
log f (xk ) −
log m
2
términos de la función exponencial que mejor se ajusta.
✔ Nos valemos del BIC para encontrar el punto de corte óptimo donde partir el dominio.
x ∈ Aj , j = 1, . . . , l ,
i =0
Función MTE unidimensional
f (x ) = a0,j +
n
X
x ∈ Aj , j = 1, . . . , l ,
ai ,j exp{bi ,j x },
Implementación
i =1
Los método desarrollados han sido realizados en R.
−1
0
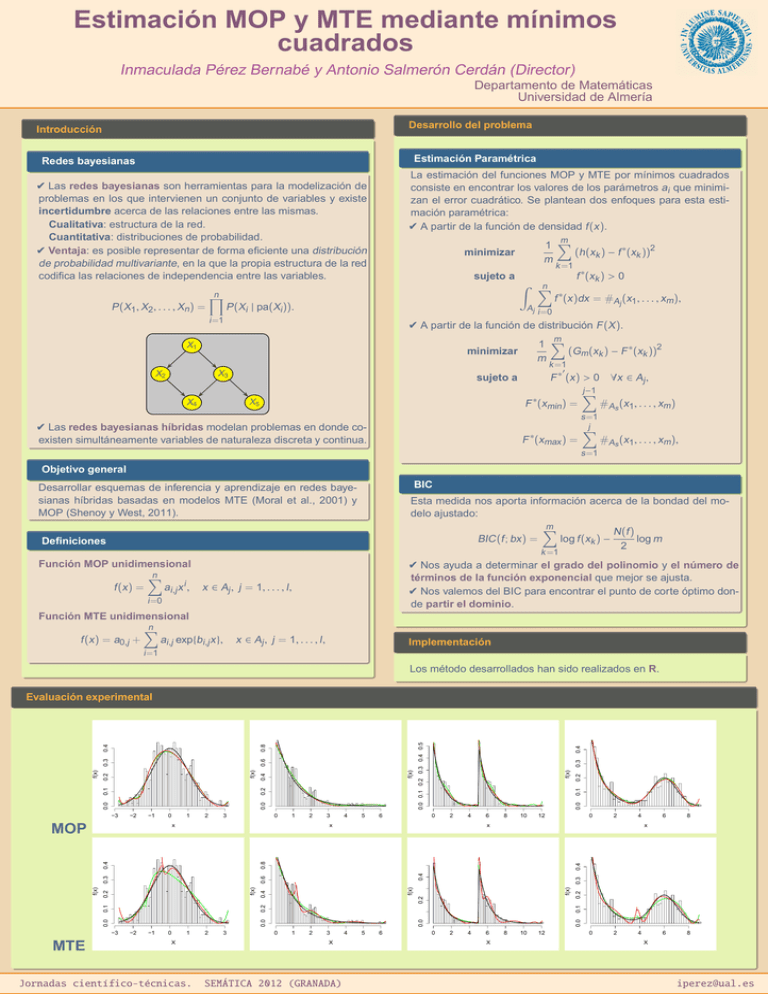
MOP
1
2
3
1
2
5
6
0.4
0.3
2
4
6
8
10
12
0
−1
0
1
X
Jornadas científico-técnicas.
2
3
4
6
8
6
8
0.2
f(x)
f(x)
0.3
0.4
0.4
0.8
0.6
−2
2
x
0
1
2
3
X
SEMÁTICA 2012 (GRANADA)
4
5
6
0.0
0.0
0.1
0.2
0.0
−3
0.2
0.1
0.0
0
x
0.4
f(x)
0.3
0.2
0.0
0.1
f(x)
4
x
0.4
x
3
f(x)
f(x)
0
0.2
−2
0.0 0.1 0.2 0.3 0.4 0.5
0.8
0.6
0.2
0.0
−3
MTE
0.4
f(x)
0.2
0.0
0.1
f(x)
0.3
0.4
Evaluación experimental
0
2
4
6
X
8
10
12
0
2
4
X
iperez@ual.es