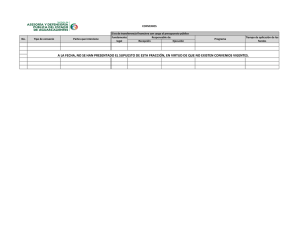
2 t·C AUC tt· 2 CC AUC

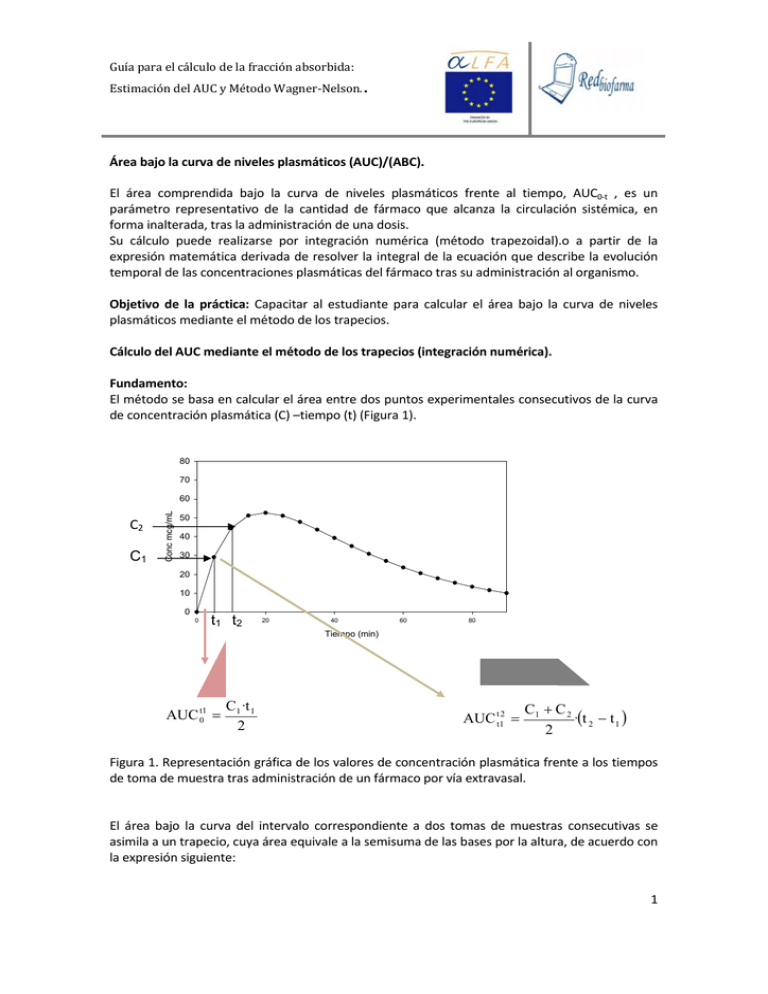
Guíaparaelcálculodelafracciónabsorbida:
EstimacióndelAUCyMétodoWagner‐Nelson..
Área bajo la curva de niveles plasmáticos (AUC)/(ABC). El área comprendida bajo la curva de niveles plasmáticos frente al tiempo, AUC0‐t , es un parámetro representativo de la cantidad de fármaco que alcanza la circulación sistémica, en forma inalterada, tras la administración de una dosis. Su cálculo puede realizarse por integración numérica (método trapezoidal).o a partir de la expresión matemática derivada de resolver la integral de la ecuación que describe la evolución temporal de las concentraciones plasmáticas del fármaco tras su administración al organismo. Objetivo de la práctica: Capacitar al estudiante para calcular el área bajo la curva de niveles plasmáticos mediante el método de los trapecios. Cálculo del AUC mediante el método de los trapecios (integración numérica). Fundamento: El método se basa en calcular el área entre dos puntos experimentales consecutivos de la curva de concentración plasmática (C) –tiempo (t) (Figura 1). 80
70
C2 C1
Conc mcg/mL
60
50
40
30
20
10
0
0
t1 t2
20
40
60
80
Tiempo (min)
AUC 0t1 
C1·t 1
2
AUC tt12 
C1  C 2
·t 2  t 1  2
Figura 1. Representación gráfica de los valores de concentración plasmática frente a los tiempos de toma de muestra tras administración de un fármaco por vía extravasal. El área bajo la curva del intervalo correspondiente a dos tomas de muestras consecutivas se asimila a un trapecio, cuya área equivale a la semisuma de las bases por la altura, de acuerdo con la expresión siguiente: 1 Guíaparaelcálculodelafracciónabsorbida:
EstimacióndelAUCyMétodoWagner‐Nelson..
C  C2
Area  t· 1
2
Siendo Δt=t2‐t1 Cuando el fármaco se administra por vía extravasal el primer trapecio es un triangulo y el área se calcula a partir de la ecuación siguiente: AUC 0t1 
C1·t1
2
Cuando el fármaco se administra por vía intravenosa el primer trapecio se calcula a partir de la siguiente expresión: AUC0t1 
C 0  C1
 t 1  0 
2
En la que C0 es la concentración plasmática para tiempo cero y se calcula mediante regresión lineal de los pares de valores experimentales (Cp, t) obtenidos para los dos primeros tiempos de toma de muestra. El área total bajo la curva desde tiempo cero hasta el último tiempo (t) en el que se dispone de valor experimental de concentración plasmática, AUC0‐t, equivale a la suma de las áreas de todos los trapecios considerados en este periodo de tiempo: C  C2
t
AUC 0t  0 t· 1
2
El valor de AUCt‐ se obtiene a partir de la siguiente expresión: AUCt 
Ct
k
En la que Ct representa el último valor experimental de concentración plasmática y k la pendiente de la recta de regresión de los pares de valores experimentales de los logaritmos neperianos de concentración plasmática y tiempo que definen una recta en escala semilogarítmica. El cálculo del área total bajo la curva, AUC0‐, se obtiene de acuerdo con la siguiente expresión. AUC 0  AUC 0t  AUC t 2 Guíaparaelcálculodelafracciónabsorbida:
EstimacióndelAUCyMétodoWagner‐Nelson..
En el programa Biofarmacia Moderna se describe el fundamento del método en el módulo de farmacocinética bajo el tópico Biodisponibilidad (cálculo) del que se ha extraído la figura siguiente. 3 Guíaparaelcálculodelafracciónabsorbida:
EstimacióndelAUCyMétodoWagner‐Nelson..
Cálculo de la fracción de dosis absorbida. Método de Wagner y Nelson Objetivos. 1. Capacitar al estudiante para estimar el porcentaje o fracción absorbida frente al tiempo a partir de los pares de valores experimentales de concentración plasmática‐tiempo utilizando el método de Wagner Nelson. 2. Capacitar al estudiante para describir los modelos de absorción sencillos relacionados con el modelo monocompartimental. Método de Wagner‐Nelson [ref: J.G. Wagner and E. Nelson. Percent absorbed time plots derived from blood level and/or urinary excretion data. J. Pharm. Sci. 52:610‐611 (1963)]: Para utilizar este método se dispone de los pares de valores experimentales de concentración plasmática del fármaco (Cp) obtenidos para cada tiempo de toma de muestra (t) tras la administración del fármaco por la vía y forma farmacéutica seleccionadas. Este método es válido para cualquier vía y forma de administración, independientemente del orden que siga el proceso de la absorción e independientemente de que ésta sea o no completa. Es un método cuantitativo. Fundamento: En cualquier instante, la cantidad de medicamento absorbido (Qa) es igual a la cantidad de medicamento existente en el organismo (Q) más la cantidad eliminada (Qe): Qa  Q  Qe En el modelo monocompartimental, la concentración plasmática es la misma que existe en el resto de compartimentos acuosos del organismo. Por consiguiente, las cantidades Qa, Q y Qe, se pueden expresar como concentraciones si se dividen por el volumen de distribución del fármaco (Vd). Así el balance anterior expresado en concentración adopta la siguiente expresión: At  C  E en la que At equivale a la concentración absorbida acumulada (es decir, la que habría en plasma si no existieran procesos de eliminación simultáneos). Este valor se calcula como suma de la concentración plasmática (C), y la concentración eliminada (E). La concentración plasmática es el dato experimental y la concentración eliminada se calcula a partir de la siguiente expresión: t
E  k el  C  dt 0
4 Guíaparaelcálculodelafracciónabsorbida:
EstimacióndelAUCyMétodoWagner‐Nelson..
A su vez deducida como se indica a continuación: ka
A
C
kel
E
dE
 k el  C dt
dE  k el  C  dt 
E
E0
t
dE  k el  C  dt 0
t
E  E 0  k el   C  dt  k el  AUC0t 0
En tiempo cero la concentración de fármaco eliminada es igual a cero (E0=0), por lo tanto: E  k el  AUC 0t kel se obtiene a partir de la fracción final exponencial de la curva de concentración plasmática tiempo y AUC 0‐t representa el área bajo la curva de concentración plasmática tiempo entre 0 y t (que se calcula utilizando el método de los trapecios). Así, los valores de las concentraciones absorbidas acumuladas (At) para cada tiempo se calculan de acuerdo con la expresión siguiente: t
At  C  k el   C  dt 0
Al representar gráficamente los valores de la concentración absorbida para cada tiempo de toma de muestra se obtiene una curva ascendente que se hace asintótica cuando cesa la absorción (Figura 2). 5 Guíaparaelcálculodelafracciónabsorbida:
EstimacióndelAUCyMétodoWagner‐Nelson..
Figura 2: Representación gráfica de las concentraciones absorbidas acumuladas (At) para cada tiempo de toma de muestra (t). Tras absorberse la cantidad de fármaco máxima susceptible de hacerlo los valores de At se mantienen constantes y equivale a A, que es la cantidad máxima de fármaco absorbida y equivalente matemáticamente a: 
A   k el   C  dt 0
Fracción de dosis absorbida. El cociente entre la concentración absorbida a un tiempo t y la concentración máxima absorbida (At/A) representa la fracción absorbida, de la cantidad total que se absorberá, que puede ser igual o inferior a la dosis administrada. En caso de que la absorción sea completa el valor de la concentración absorbida acumulada para tiempo infinito (A) multiplicado por el volumen de distribución del fármaco (Vd) equivale a la dosis administrada. Sin embargo, cuando la absorción no es completa este producto (A∙Vd) equivale una fracción de la dosis administrada (f ∙D), en la que f es la biodisponibilidad o fracción de la dosis administrada que llega de forma inalterada a la circulación sistémica. La fracción máxima absorbida será la unidad (o 100 cuando se expresa en forma de porcentaje). En la figura 3 se muestra la representación gráfica de la fracción absorbida en función del tiempo de toma de muestra. 6 Guíaparaelcálculodelafracciónabsorbida:
EstimacióndelAUCyMétodoWagner‐Nelson..
Figura 3: Representación gráfica de la fracción de dosis absorbida (At/A) para cada tiempo de toma de muestra (t). Cálculo de la constante de velocidad de absorción Por diferencia entre el valor A (cantidad máxima de fármaco absorbida) y los valores de At, se puede calcular la cantidad de fármaco remanente en el lugar de absorción expresada como concentración plasmática: 
t
A   At  k el   C  dt  C  k el   C  dt  

0
0
Cuando la cinética de absorción es de primer orden la constante de velocidad de absorción de primer orden, ka, se obtiene tras hacer la regresión lineal de los valores de los logaritmos neperianos de (A ‐ At) frente a los tiempos de toma de muestra de acuerdo con la siguiente ecuación general: ln  A  At   ln A  k a  t La constante de velocidad de absorción, ka, se expresa en unidades de tiempo recíproco. A partir de ella se puede calcular la semivida de absorción, t1/2a, que se expresa en unidades de tiempo. t1 
2
a
ln 2 0.693

ka
ka
7 Guíaparaelcálculodelafracciónabsorbida:
EstimacióndelAUCyMétodoWagner‐Nelson..
La constante de velocidad de absorción también se puede calcular a partir de los valores del índice de absorción (At/A) obtenido para cada tiempo de toma de muestra. Si se realiza la diferencia entre la fracción máxima absorbida (1) y la fracción absorbida a un determinado tiempo se obtiene la expresión: 1
At
A
 1  e  ka·t ; 100  t  100  e  ka·t A
A
Que en forma logarítmica se expresa de acuerdo con las ecuaciones: 
ln1 

At
A

  ln 1  k a  t 

A
ln100  t
A


  ln 100  k a  t 
El balance de Wagner Nelson no implica ningún supuesto respecto a la cinética de la absorción. Por consiguiente, de la misma forma se podría calcular la constante de velocidad de absorción de orden cero en caso de que la cinética del proceso de absorción se ajustara mejor a una cinética de orden cero. Ecuación de la curva acumulativa La ecuación de la curva acumulativa se deduce al despejar el valor de At en la ecuación la expresión matemática de la desaparición de fármaco en el lugar de absorción como se indica a continuación: ln A   At   ln A   k a  t A   At  A   e  k a t At  A   A   e  k a t o bien: At  A   1  e  k a t O en forma de fracción: 



At
 1  e  k a t A
8 Guíaparaelcálculodelafracciónabsorbida:
EstimacióndelAUCyMétodoWagner‐Nelson..
Cálculo del periodo de latencia Mediante el método de Wagner‐Nelson también se puede calcular el periodo de latencia previo a la absorción. Cuando existe periodo de latencia, se obtiene una curva acumulativa desplazada a la derecha en el eje de ordenadas (figura siguiente). En tiempo cero el valor de (A ‐ At) no coincide con el valor de A, sino que estos valores coinciden en un tiempo t0, esto es, el tiempo de latencia. t0 El tiempo equivalente al periodo de latencia se calcula a partir de la expresión matemática que se deduce a continuación. En tiempo t0 coinciden A y (A ‐ At). A   A t   A 0  e  kat 0 Por consiguiente, como en t= t0, A=(A ‐ At) A  A 0  e  kat0 y tomando logaritmos neperianos ln A  ln A 0  k a  t 0 que transponiendo y despejando se obtiene la expresión matemática siguiente que permite calcular el periodo de latencia: A

ln 0

A

t0  
ka
9 Guíaparaelcálculodelafracciónabsorbida:
EstimacióndelAUCyMétodoWagner‐Nelson..
Ventajas y limitaciones del método de Wagner‐Nelson 1. Permite calcular el tiempo que define el periodo de latencia. 2. La curva acumulativa siempre alcanza el 100% aunque la biodisponibilidad no sea completa. Esto le confiere un sentido cuantitativo al método. Así, cuando la absorciones completa, el valor de A debe ser igual al valor de C0 obtenido a la misma dosis por vía intravenosa: Si la absorción es completa A ∙Vd= D Si la absorción no es completa A ∙Vd=f ∙D 3. El balance de Wagner Nelson no implica ningún supuesto respecto a la cinética de la absorción. 4. La kel se obtiene de la fase terminal monoexponencial de la curva de concentración plasmática tiempo del fármaco administrado por vía extravasal. Sin embargo, en un modelo Flip‐Flop esta estimación no es correcta. 5. Únicamente si se tienen datos del fármaco administrado por vía intravenosa se puede tener seguridad en el valor de la constante de velocidad de eliminación, kel, que se maneja. 10 Guíaparaelcálculodelafracciónabsorbida:
EstimacióndelAUCyMétodoWagner‐Nelson..
Ejercicios 1. Tras administración por vía oral de una dosis de 400 m de carbamazepina a pacientes adultos se obtienen los siguientes calores de concentración plasmática y tiempo: tiempo Concentración horas mcg/mL 0 0 1 1.6 5 3.5 7 4.8 10 5.8 25 5.7 48 3.2 60 2.2 72 1.7 Calcule la fracción máxima absorbida utilizando el método de Wagner‐Nelson. 2. Respetando el periodo de lavado se administra a un paciente, una dosis de 250 mg de un antibiótico por vía intravenosa, una dosis de 500 mg en forma de suspensión por vía oral y una dosis de 500 mg en forma de cápsulas. Los valores de concentración plasmática‐
tiempo obtenidos se indican en el tabulado siguiente. Calcule en cada situación el AUC y la fracción de fármaco absorbida cuando el fármaco se administra por vía oral. Suspensión oral 500 Cápsulas orales 500 Tiempo IV 250 mg mg mg Concentración Concentración Concentración horas (mg/L) (mg/L) (mg/L) 1 6.3 5 3.1 2 5 7 4.7 3 4 7.4 5.2 4 3.2 7 5.3 6 2 5.4 4.5 8 1.3 3.7 3.4 12 0.5 1.6 1.7 11