Extensión de la Regla de Sarrus para calcular la

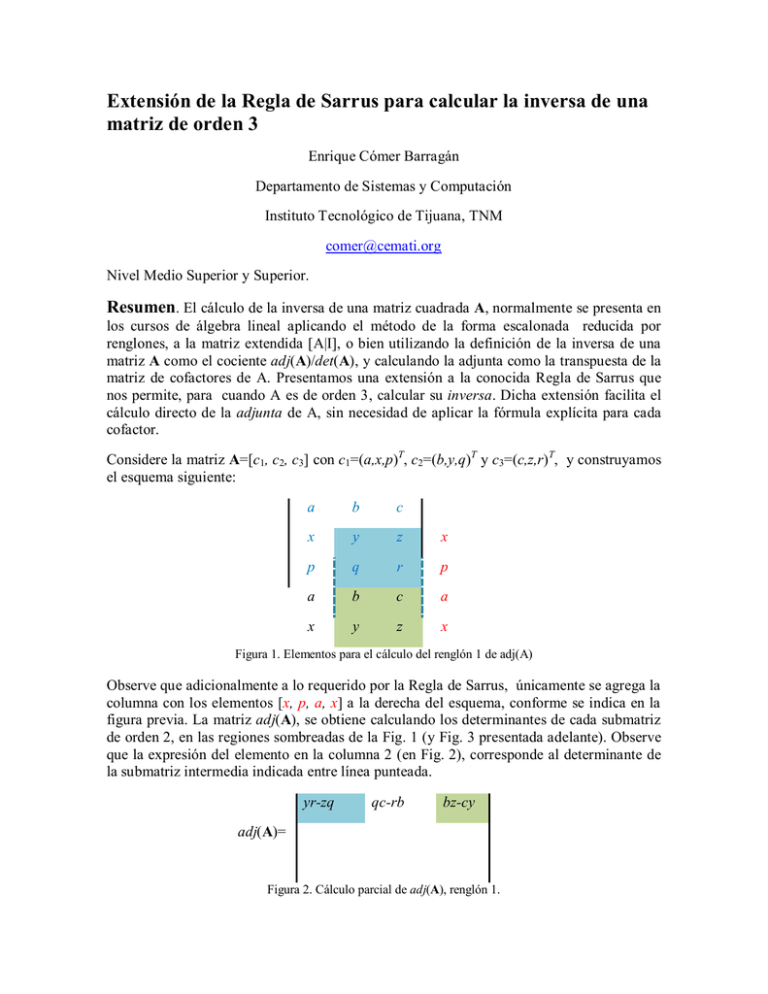
Extensión de la Regla de Sarrus para calcular la inversa de una
matriz de orden 3
Enrique Cómer Barragán
Departamento de Sistemas y Computación
Instituto Tecnológico de Tijuana, TNM
comer@cemati.org
Nivel Medio Superior y Superior.
Resumen. El cálculo de la inversa de una matriz cuadrada A, normalmente se presenta en
los cursos de álgebra lineal aplicando el método de la forma escalonada reducida por
renglones, a la matriz extendida [A|I], o bien utilizando la definición de la inversa de una
matriz A como el cociente adj(A)/det(A), y calculando la adjunta como la transpuesta de la
matriz de cofactores de A. Presentamos una extensión a la conocida Regla de Sarrus que
nos permite, para cuando A es de orden 3, calcular su inversa. Dicha extensión facilita el
cálculo directo de la adjunta de A, sin necesidad de aplicar la fórmula explícita para cada
cofactor.
Considere la matriz A=[c1, c2, c3] con c1=(a,x,p)T, c2=(b,y,q)T y c3=(c,z,r) T, y construyamos
el esquema siguiente:
a
b
c
x
y
z
x
p
q
r
p
a
b
c
a
x
y
z
x
Figura 1. Elementos para el cálculo del renglón 1 de adj(A)
Observe que adicionalmente a lo requerido por la Regla de Sarrus, únicamente se agrega la
columna con los elementos [x, p, a, x] a la derecha del esquema, conforme se indica en la
figura previa. La matriz adj(A), se obtiene calculando los determinantes de cada submatriz
de orden 2, en las regiones sombreadas de la Fig. 1 (y Fig. 3 presentada adelante). Observe
que la expresión del elemento en la columna 2 (en Fig. 2), corresponde al determinante de
la submatriz intermedia indicada entre línea punteada.
yr-zq
qc-rb
bz-cy
adj(A)=
Figura 2. Cálculo parcial de adj(A), renglón 1.
De forma similar, podemos obtener los otros dos renglones de la adj(A), en base al
siguiente esquema:
a
b
c
a
b
c
x
y
z
x
x
y
z
x
p
q
r
p
p
q
r
p
a
b
c
a
a
b
c
a
x
y
z
x
x
y
z
x
(a)
(b)
Figura 3. Cálculo de renglones 2 (b) y 3 (a) de adj(A)
El cálculo de adj(A) se completa conforme lo indicado en los incisos (a) y (b) de la Fig. 3.
adj(A)=
yr-zq
qc-rb
bz-cy
zp-xr
ra-pc
cx-az
xq-yp
pb-qa
ay-bx
(1)
Como puede verificarse fácilmente, las expresiones en cada uno de los elementos de adj(A)
en (1) corresponden exactamente a los elementos de la transpuesta de la matriz de
cofactores: Aij = (-1)i+j det(Mij), donde Mij es el menor asociado a la posición i,j de la
matriz A.
A partir de los resultados de la adj(A) y el cálculo de det(A) mediante la Regla de Sarrus,
podemos calcular directamente la matriz inversa de A.
Se presentarán ejemplos en un contexto educativo asociado a criptología básica (ver p. ej.
José de Jesús Angel Angel, 2011), y acertijos modelables como un sistema lineal de orden
3 parametrizado, donde el propósito es desarrollar la agilidad mental con números
racionales y expresiones simbólicas, asi como realizar cálculos exactos de manera eficiente
sin apoyo de calculadoras, como puede ser el caso en algunos concursos de matemáticas o
en exámenes donde se evalúen competencias matemáticas básicas.
Observación. Debido a la simplicidad del esquema indicado en (1), una de sus ventaja s es
la reducción del número potencial de errores, en comparación con los dos métodos
comentados al inicio del presente resumen. [Rev. 2015.01.09]
Referencias bibliográficas:
José de Jesús Angel Angel. (2011). Criptografía: ejercicios de cifrado usando matrices. 2015.01.09, de
MathCon: the mathematics firm Sitio web: http://www.math.com.mx/docs/cur/cur_1_002_Criptografia.pdf