20) Las puntuaciones obtenidas por 24 personas en dos test sobre
Anuncio
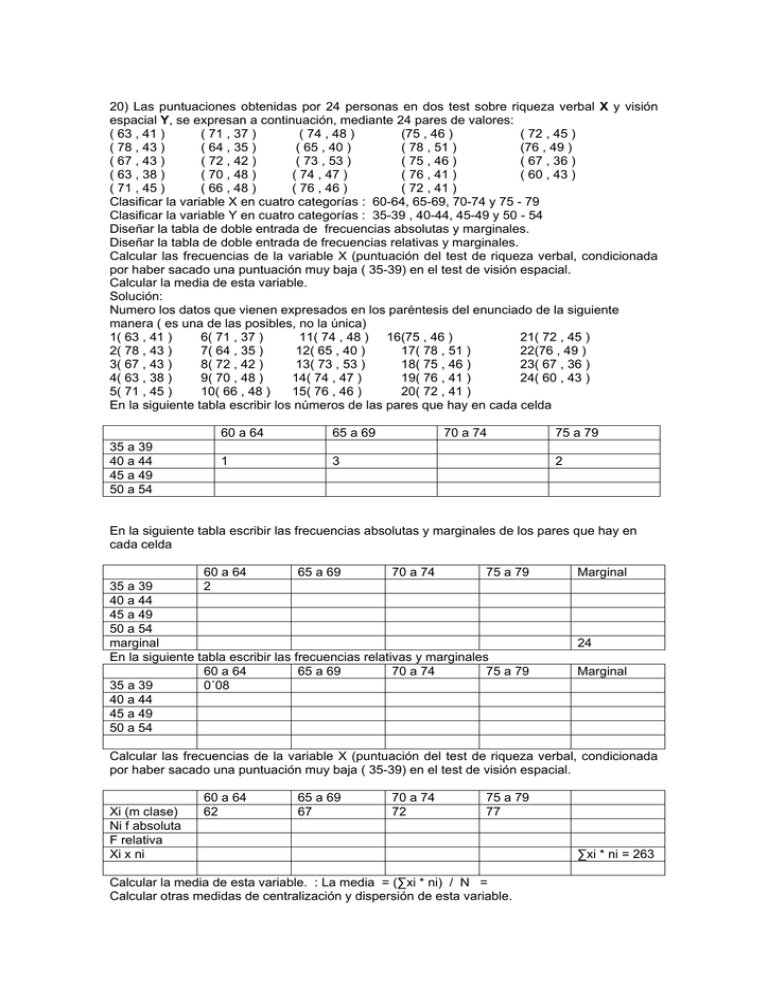
20) Las puntuaciones obtenidas por 24 personas en dos test sobre riqueza verbal X y visión espacial Y, se expresan a continuación, mediante 24 pares de valores: ( 63 , 41 ) ( 71 , 37 ) ( 74 , 48 ) (75 , 46 ) ( 72 , 45 ) ( 78 , 43 ) ( 64 , 35 ) ( 65 , 40 ) ( 78 , 51 ) (76 , 49 ) ( 67 , 43 ) ( 72 , 42 ) ( 73 , 53 ) ( 75 , 46 ) ( 67 , 36 ) ( 63 , 38 ) ( 70 , 48 ) ( 74 , 47 ) ( 76 , 41 ) ( 60 , 43 ) ( 71 , 45 ) ( 66 , 48 ) ( 76 , 46 ) ( 72 , 41 ) Clasificar la variable X en cuatro categorías : 60-64, 65-69, 70-74 y 75 - 79 Clasificar la variable Y en cuatro categorías : 35-39 , 40-44, 45-49 y 50 - 54 Diseñar la tabla de doble entrada de frecuencias absolutas y marginales. Diseñar la tabla de doble entrada de frecuencias relativas y marginales. Calcular las frecuencias de la variable X (puntuación del test de riqueza verbal, condicionada por haber sacado una puntuación muy baja ( 35-39) en el test de visión espacial. Calcular la media de esta variable. Solución: Numero los datos que vienen expresados en los paréntesis del enunciado de la siguiente manera ( es una de las posibles, no la única) 1( 63 , 41 ) 6( 71 , 37 ) 11( 74 , 48 ) 16(75 , 46 ) 21( 72 , 45 ) 2( 78 , 43 ) 7( 64 , 35 ) 12( 65 , 40 ) 17( 78 , 51 ) 22(76 , 49 ) 3( 67 , 43 ) 8( 72 , 42 ) 13( 73 , 53 ) 18( 75 , 46 ) 23( 67 , 36 ) 4( 63 , 38 ) 9( 70 , 48 ) 14( 74 , 47 ) 19( 76 , 41 ) 24( 60 , 43 ) 5( 71 , 45 ) 10( 66 , 48 ) 15( 76 , 46 ) 20( 72 , 41 ) En la siguiente tabla escribir los números de las pares que hay en cada celda 35 a 39 40 a 44 45 a 49 50 a 54 60 a 64 65 a 69 1 3 70 a 74 75 a 79 2 En la siguiente tabla escribir las frecuencias absolutas y marginales de los pares que hay en cada celda 60 a 64 65 a 69 70 a 74 75 a 79 35 a 39 2 40 a 44 45 a 49 50 a 54 marginal En la siguiente tabla escribir las frecuencias relativas y marginales 60 a 64 65 a 69 70 a 74 75 a 79 35 a 39 0´08 40 a 44 45 a 49 50 a 54 Marginal 24 Marginal Calcular las frecuencias de la variable X (puntuación del test de riqueza verbal, condicionada por haber sacado una puntuación muy baja ( 35-39) en el test de visión espacial. Xi (m clase) Ni f absoluta F relativa Xi x ni 60 a 64 62 65 a 69 67 70 a 74 72 75 a 79 77 Calcular la media de esta variable. : La media = (∑xi * ni) / N = Calcular otras medidas de centralización y dispersión de esta variable. ∑xi * ni = 263 21) La tabla siguiente da las frecuencias observadas de las variables CI (coeficiente de inteligencia) y RT (rendimiento en el trabajo), de 400 personas que realizaron un curso de formación. RT Mal CI Bajo Medio Alto Total 67 42 10 119 Regular 64 76 23 163 Bien Total 25 56 37 118 156 174 70 400 Suponiendo que se trata de variables que no están en absoluto relacionadas (independientes) calcular la tabla de frecuencias esperadas. Calcular la tabla de frecuencias relativas. Calcular la distribución de frecuencias del rendimiento en el trabajo, condicionadas por un coeficiente intelectual medio. Calcular la distribución de frecuencias del coeficiente intelectual, condicionado por un rendimiento en el trabajo alto. 22) Se están estudiando los pesos en Kgs. y las alturas en cms. de 70 personas. Los datos están recogidos en la siguiente tabla: Pesos/Talla [159,161) 47-49 3 50-52 2 53-55 1 56-58 0 59-61 0 [161,163) 2 3 3 0 0 [163,165) 2 4 6 1 0 [165,167) 1 2 8 2 2 [167,169) 0 2 5 8 4 [169,171) 0 1 1 3 4 a) Calcular el peso medio y la talla media. ¿Cuál de las dos medidas presenta mayor dispersión? b) Hallar la distribución de las tallas de los individuos condicionada porque pesen de 53 a 55 kilos. Hallar también la distribución de los pesos condicionada porque las alturas estén en el intervalo [161 , 167). Calcular la media y la varianza de las dos distribuciones condicionadas.