Document
Anuncio

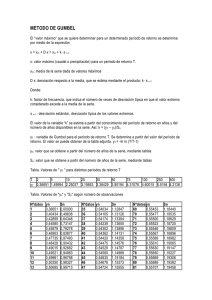
Luisa Fernanda Mosquera Deisy Jhoana Andrade Edinson Solarte Manuel A. Plaza 1. Algoritmo 0. Inicio 1. for (i=1; i<TAM; i++) 2. for j=0 ; j<TAM - 1; j++) 3. if (lista[j] > lista[j+1]) 4. temp = lista[j]; 5. lista[j] = lista[j+1]; 6. lista[j+1] = temp; 7. fin 0. Inicia el programa 1.Primer ciclo indica el numero de iteraciones que se van ha realizar para ordenar el arreglo. Este numero ya esta definido, por ello no deja de recorrer el arreglo si esta ordenado. 2. Segundo ciclo anidado que recorre el arreglo internamente , para iniciar el ordenamiento. 3. Compara las posiciones contiguas del arreglo , si esta condición se cumple se realiza el intercambio. 4. Asigna el valor de la posición j de arreglo a una temporal. 5. Asigna el valor de la siguiente a la posición J. 6. Asigna el valor de la temporal a J + 1. 7. Terminar. 2. Análisis del algoritmo 0. Inicio 1. for (i=1; i<TAM; i++) 2. for( j=1 ; j<TAM ; j++) 3. if (lista[j] > lista[j+1]) 4. temp=lista[j]; 5. lista[j]=lista[j+1]; 6. lista[j+1] = temp; 7. fin Costo Veces C1 n C2 C3 C4 C5 C6 (*)n(n-1) (n-1)(n-1) (n-1)(n-1) (n-1)(n-1) (n-1)(n-1) T (n) =C1(n)+C2(n-1)(n)+C3(n-1)(n-1)+C4(n-1)(n-1))+C5(n-1)(n-1)) +C6(n-1)(n-1) T (n) = (C2+C3+C4+C5+C6)n2 + (C1-C2-2C3-2C4-2C5-2C6)n + (C3+C4+C5+C6) T (n) = a.n2 +b.n+ c f(n) =an2+bn+c 3. Ejemplo de Ejecución 1. Ejemplo de ejecución en caso promedio Esta es nuestra lista: 4 - 3 - 5 - 2 - 1 Tenemos 5 elementos. Es decir, TAM toma el valor 5. Comenzamos comparando el primero con el segundo elemento. 4 es mayor que 3, así que intercambiamos. Ahora tenemos: 3-4-5-2-1 Ahora comparamos el segundo con el tercero: 4 es menor que 5, así que no hacemos nada. Continuamos con el tercero y el cuarto: 5 es mayor que 2. Intercambiamos y obtenemos: 3-4-2-5-1 Comparamos el cuarto y el quinto: 5 es mayor que 1. Intercambiamos nuevamente: 3-4-2-1-5 Repitiendo este proceso vamos obteniendo los siguientes resultados: 3-2-1-4-5 2-1-3-4-5 1-2-3-4-5 • Mejor Caso T(n)=C1.n+C2(n2- n)+0+0+0+0 T(n)=C1.n + C2n2- C2.n = (C2) n2 + (C1- C2) n F(n)= a.n2 + b.n 5. Cotas F(n)= Ω(n2) • Peor Caso T (n) = C1n2 + C2.n + C3 F (n) = an2 + b.n + c Lim = an2 + b.n + c = Lim an2 + b.n + c = Lim a + Lim b + Lim c n->α n2 n->α n2 n2 n2 n->α n->α n n->α n2 =a Por la regla del limite decimos que: F (n) = O(n2) y se cumple para F(n) = θ(n2) 6. Simulación del comportamiento Cotas 30,000 R2 = 1 Tiempo de ejecucion 25,000 20,000 15,000 Peor Caso Mejor caso 10,000 Caso Promedio Polinómica (Peor Caso) 5,000 0,000 5000 10000 15000 20000 25000 30000 N° Datos 35000 40000 45000 50000 7. Posibles Variaciones del Algoritmo ALGORITMO MEJORADO 1. Int sw; 2. for (i=1; i<TAM; i++) 3. Sw=0; 4. for j=1 ; j<TAM –i+1; j++) 5. if (lista[j] > lista[j+1]) 6. sw=1; 7. temp = lista[j]; 8. lista[j] = lista[j+1]; 9. lista[j+1] = temp; 10. if (sw==0) 11. i=TAM; 50 00 10 00 0 15 00 0 20 00 0 25 00 0 30 00 0 35 00 0 40 00 0 45 00 0 50 00 0 Tiempo de ejecución Comportamiento 20 18 16 14 12 serie 1 10 Serie2 8 Serie3 6 4 2 0 Nº Datos