Unidad 7

UNIDAD TEMÁTICA VII
INTEGRACIÓN ENERGÉTICA – SÍNTESIS DE REDES DE INTERCAMBIO
CALÓRICO
VIII.1 INTRODUCCIÓN
Una vez conocidas las temperaturas, caudales, composición, estado de agregación y
contenido calórico de todas las corrientes del proceso. Y por otro lado las demandas de
potencia para bombeo y compresión, es posible integrar toda la energía puesta en
juego en el proceso, de manera tal que el calor de las corrientes que necesitan ser
enfriadas ó condensadas nos permita calentar las corrientes frías que necesitan ser
calentadas ó vaporizadas, además de proveer potencia a los compresores desde las
turbinas y maquinas térmicas cuando ello es posible.
Si bien la integración energética final del proceso se lleva a cabo en la etapa de diseño
detallado del proceso, cuando se conocen los balances rigurosos de calor y materia, en
aquellos procesos que son energéticamente intensivos, la integración energética es
imprescindible en la etapa de síntesis preliminar del flow, porque muchas veces define
la diferencia entre dos alternativas posibles para un mismo proceso.
A fin de simplificar el análisis vamos a despreciar la posibilidad de utilizar las corrientes
de alto contenido energético para satisfacer demandas de potencia y nos concentramos
en la síntesis de una Red de Intercambio Calórico (RIC) lo mas eficiente posible. A tal
efecto suponemos que N1 corrientes calientes de proceso con temperatura de entrada
(fuente) y salida (objetivo) conocidas: Tshi y Tthi , i = 1,..., N1 son enfriadas por N2
corrientes frías de proceso con temperaturas de entrada y salida conocidas: Tscj y Ttcj , j
= 1,..., N2 como se muestra en figura 1.a.
Dado que por lo general el requerimiento de enfriamiento de las corrientes calientes no
es igual a la disponibilidad de las corrientes frías, que algunas temperaturas de entrada
no son lo suficientemente altas o bajas para lograr las temperaturas de salida
deseadas, y que existen otras restricciones de proceso, resulta siempre necesario
proveer uno o más intercambiadores de calor auxiliares para calentamiento o
enfriamiento, que utilizan servicios auxiliares de vapor (agua caliente) o agua de
enfriamiento.
1
Por lo general a la red de intercambio entre corrientes de proceso, se la conoce como
Red Interna o Interior, y a los intercambios entre corrientes de procesos y servicios
auxiliares como Red Auxiliar. En figura 1b, se muestran esquemáticamente ambas
redes.
Dado que el objetivo principal de la síntesis es obtener la RIC más eficiente y
económica posible, es necesario contar con una medida simple de perfomance o
bondad económica, que nos permita evaluar y comparar diversas alternativas posibles
de la RIC. Una medida muy simple y usada es el Costo Anualizado CA:
C A = r (C TCI ) + COS
(1)
Donde CTCI es la Inversión Total de Capital, COS es el Costo Total de Fabricación
incluidas las expensas por ventas (a veces se lo denomina Costo de Ventas), y r es el
Retorno Anual Sobre la Inversión (0.20 – 0.30). Dado que nuestro propósito es la
evaluación de alternativas por comparación relativa, es suficiente considerar CTCI como
la suma de los costos de compra (Costo Base) de cada uno de los intercambiadores de
la red, sin incluir costos de instalación y otros costos asociados. Dicho costo puede
estimarse a partir de una correlación exponencial basada en el área de transferencia de
calor, donde el área se calcula como:
A = Q (UFT ∆TLM )
(2)
Debe observarse que el concepto de Costo Anual Total, es básicamente el mismo que
el de Potencial Económico propuesto por Douglas en su método de Decisión
Jerárquica. El concepto de tasa de retorno, o Retorno Anual sobre la Inversión esel
mismo, y permite anualizar (poner sobre base de tiempo) la inversión de capital, a fin de
sumarla al costo de fabricación, o lo que es lo mismo, al costo de operación.
2
Figuras 1
Donde Q es el calor transferido, U es un coeficiente total de transferencia, FT es el
factor de corrección para intercambiadores de múltiples pasos, y ∆TLM es la diferencia
de temperatura logarítmica media. Para propósitos de evaluación de alternativas, se
utilizan valores promedios o genéricos para U y FT. Para el COS resulta apropiado
3
aproximarlo como el costo total anual de servicios de calentamiento y enfriamiento,
usando vapor y agua de enfriamiento. Con estas aproximaciones, podemos escribir el
Costo Anualizado CA como:

CA = r ∑CP,
 i
Ii
+ ∑CP,
j


A j  + s ⋅ Fs + (cw)Fcw

(3)
Donde CP,Ii y CP,Aj son los costos de compra o base de los intercambiadores de las
redes interna y auxiliar respectivamente, Fs es el caudal anual de vapor (kg/año), s es el
costo unitario del vapor ($/kg), Fcw el caudal anual de agua de enfriamiento (kg/año), y
cw el costo unitario de agua de enfriamiento ($/kg) Cuando se utilizan otros servicios
tales como refrigerante, aire, fuel, deben agregarse términos adicionales. El costo CP se
lo puede estimar en base a una correlación potencial del tipo:
C p = 450.A 0.7
(4)
Si bien existen diversas aproximaciones para optimizar la ecuación 3, la mas
ampliamente usada se desarrollo después de la crisis del petróleo (1973) que generó
una crisis mundial de energía. El procedimiento se basa en dos etapas:
1. Se diseña una RIC en base a un consumo mínimo de servicios de calentamiento y
enfriamiento, que normalmente requiere un gran numero de intercambiadores de calor.
Cuando el costo del combustible es muy alto, la solución encontrada es cercana a la
óptima.
2. El numero de intercambiadores de calor se reduce a un mínimo, a expensas de mayor
consumo de servicios
Obviamente en la medida que se implementa la etapa 2 y se disminuye la cantidad de
intercambiadores (disminuye la Inversión de Capital), aumenta el consumo de servicios
aumentando el costo de operación. Ello plantea un problema de optimización que
depende de varios factores, sin embargo cuando el costo de combustible es alto, el
costo anualizado obtenido usando un consumo mínimo de servicios es cercano al
óptimo.
VIII.2 REQUERIMIENTOS MINIMOS DE SERVICIOS
4
Existen fundamentalmente dos métodos para determinar los requerimientos mínimos
de calentamiento y enfriamiento de una red de intercambiadores de calor. En ambos
métodos se obtiene los mencionados requerimientos sin necesidad de diseñar la RIC.
Además los resultados obtenidos dependen de la elección que realiza el diseñador de
la aproximación mínima de temperatura ∆Tmin. Una vez determinados los
requerimientos mínimos, es posible sintetizar la red de intercambiadores a través de un
proceso de cruzamiento de corrientes que también se puede llevar a cabo por dos
métodos diferentes.
Los dos métodos principales para determinar los Requerimientos Mínimos de
Calentamiento y Enfriamiento son:
1.
Método de los Intervalos de Temperatura
2.
Método algorítmico o de Programación Lineal
Solo veremos el primero, ya que el segundo se ve en cursos de posgrado.
METODO DEL INTERVALO DE TEMPERATURA (método TI)
Fue desarrollado por Linnhoff y Flowers (1978 a, 1978 b) siguiendo los trabajos
pioneros de Hohmann (1971). A fin de desarrollar el método, utilizaremos el ejemplo
clásico de Linnhof y Turner (1981). El método nos permite estimar los mínimos
requerimientos de calentamiento y enfriamiento de todas las redes de intercambio
posible, conocidos los requerimientos de calentamiento y enfriamiento de las corrientes
de proceso y la mínima aproximación de temperatura ∆Tmin en los intercambiadores de
calor.
Ejemplo 1
Dadas dos corrientes frías que deben ser calentadas C1 y C2 y dos corrientes calientes
que deben ser enfriadas H1 y H2, sin cambio de fase. Las condiciones y propiedades
de las mismas son las siguientes:
5
Stream
Ts (ºF)
Tt (ºF)
mCp
Q (Btu/hr)
(Btu/hr·ºF)
C1
120
235
20000
2300000
C2
180
240
40000
2400000
H1
260
160
30000
3000000
H2
250
130
15000
1800000
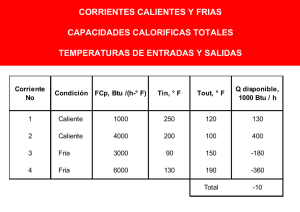
Se supone que el caudal de capacidad calorífica m.Cp = C no varía con la temperatura.
Cuando es necesario considerar dicha variación, se discretiza la corriente en varias
corrientes, donde cada uno de los segmentos involucrados corresponde a un
subintervalo de temperatura con un valor diferente de C. Observando la columna de la
derecha, se nota que las corrientes calientes deben entregar un total de 4800000 Btu/hr
y que las corrientes frías solo pueden consumir un total de 4700000 Btu/hr. Por lo tanto
de la aplicación de la 1º Ley de la termodinámica, nos queda un mínimo de 100000
Btu/hr que deben ser removidas del proceso mediante el uso de un servicio auxiliar tal
como agua de enfriamiento. Como veremos luego, dicho valor no representa el mínimo
requerimiento del servicio auxiliar, ya que de la aplicación de la 2º Ley de la
Termodinámica, dicho valor depende de ∆Tmin . A fin de ilustrar el método obtendremos
una solución para un ∆Tmin = 10ºF.
Solución: La primera etapa en la aplicación del método TI consiste en ajustar las
temperaturas de entrada y salida usando el ∆Tmin fijado previamente. Esto puede
realizarse en forma arbitraria reduciendo las temperaturas de las corrientes calientes en
un valor igual a ∆Tmin , y dejando los valores de las corrientes frías sin alterar. De esta
forma podemos definir un conjunto de intervalos de temperaturas entre cada uno de los
niveles de temperatura de las corrientes frías y calientes. Las corrientes desfasadas o
ajustadas se muestran en la siguiente tabla. En ella podemos observar los siguientes
valores o niveles de temperatura: 120, 150, 180, 235, 240, 250. Por otra parte quedan
definidos 5 intervalos de temperaturas: I1: (250 – 240); I2: (240 – 235); I3: (235 – 180); I4:
(180 – 150); I5: (150 – 120).
6
Si observamos detenidamente los rangos de temperaturas de las corrientes y los
intervalos definidos, vemos que en cada intervalo esta incluida una o más corrientes,
tanto frías como calientes. En función de ello y teniendo en cuenta que conocemos el
caudal de capacidad calorífica de cada una de las corrientes, podemos calcular el
contenido calórico de cada uno de los intervalos de acuerdo a:
∆Hi = { ∑i (m·Cp)H,i - ∑i (m·Cp)C,i } · ∆Ti
donde:
i = 1, …., Nintervalos
Nintervalos = Nº de Intervalos definidos;
Stream
Ts (ºF)
Tt (ºF)
C1
120
235
C2
180
240
H1
250
150
H2
240
120
Tabla: Temperaturas de Corrientes Calientes Ajustadas
Una forma sencilla de visualizar los intervalos de temperatura definidos y las corrientes
involucradas en cada intervalo se muestra en la figura 2
Figura 2: Intervalos de temperatura y corrientes involucradas
7
En esta figura se grafican los niveles de temperatura en forma decreciente mediante
líneas horizontales, y cada una de las corrientes mediante líneas verticales. A la
derecha se indican los 5 intervalos de temperatura definidos. Como se puede observar,
las corrientes incluidas en los distintos intervalos son las siguientes: I1:(H1); I2:(H1, H2,
C2); I3:( H1, H2, C1, C2); I4(H1, H2, C1); I5:( H2, C1).
Luego mediante la ecuación de ∆Hi podemos calcular los contenidos calóricos de todos
los intervalos. Nos queda por ejemplo:
∆H1 = 30000 (250 – 240) = 300000 Btu/hr
∆H2 = (30000 + 15000 – 40000)·(240 – 235) = 25000 Btu/hr
Una vez calculados todos los contenidos calóricos de los intervalos, se puede
representar el balance de energía de cada intervalo mediante un diagrama en cascada
como el de figura 3. En el se representa los intervalos de temperatura, el balance de
energía de cada intervalo, los flujos de calor entre intervalos, y los flujos de vapor y
agua de enfriamiento que satisfacen el balance de energía.
Figura 3
8
Así por ejemplo, el intervalo 1 posee una disponibilidad de calor de 30·104 Btu/hr y por
lo tanto no necesita del servicio auxiliar de vapor (Qsteam) = 0. Luego este valor residual
de 30·104 Btu/hr (R1 = 30) lo puede transferir al intervalo 2 que a su vez posee una
disponibilidad de 2.5·104 Btu/hr, queda por lo tanto un valor residual del intervalo 2 de
R2 = 32.5.
El intervalo 3 posee un defecto de energía de (- 82.5·104 Btu/hr) y dado que el valor
residual de segundo intervalo era de 32.5, es posible satisfacer parcialmente los – 82.5
y nos quedara un valor residual en defecto R3 = - 50·104 Btu/hr.
El intervalo 4 posee una disponibilidad de 75·104 Btu/hr, y por lo tanto podemos
satisfacer los – 50 de R3. Nos queda así un residuo de R4 = 25 que nos permite luego
satisfacer el defecto de energía del intervalo 5 (∆H5 = - 15·104 Btu/hr). Nos queda así un
residuo de energía de 10·104 Btu/hr que debería ser removido mediante agua de
enfriamiento (QCW = 10). Por lo tanto solo necesitaríamos utilizar el servicio auxiliar de
agua de enfriamiento para satisfacer el balance. Lamentablemente hemos cometido un
ERROR GRAVE, dado que el intervalo 4 esta a un nivel de temperatura inferior al 3, y
estaríamos violando el 2º Principio de la Termodinámica.
Por lo tanto el residuo R3 = - 50·104 Btu/hr debe satisfacerse mediante vapor del
servicio auxiliar. En la última columna de la figura 3 se muestra el balance final con un
ingreso de energía (por vapor) de 50·104 Btu/hr, y un egreso de energía de 60·104
Btu/hr mediante agua de enfriamiento. Dichos valores constituyen los mínimos
requerimientos de calentamiento y enfriamiento que satisfacen el 1º y 2º principio de la
Termodinámica. Nótese que la diferencia: Qsteam - QCW = 50 – 60 = - 10 resulta
consistente con el primer principio.
Como puede observarse para dichos requerimientos mínimos, no fluye energía entre
los intervalos 3 y 4. Nos queda así definido el denominado PUNTO PINCH a una
temperatura de 180º para las corrientes frías y 180º + ∆Tmin = 190º para las corrientes
calientes. Su principal característica es que:
Para mantener requerimientos mínimos de energía, no se debe transferir energía
a través del pinch.
En la Tabla 1 se dan los valores de contenidos calóricos de calentamiento y
enfriamiento para cada uno de los intervalos con sus temperaturas reales. También se
incluye las cargas acumuladas comenzando desde las temperaturas más bajas.
9
Tabla 1
En la figura 4 se muestra una representación de las corrientes calientes y frías con el
punto pinch que particiona el problema. De izquierda a derecha se representan las
corrientes calientes con sus valores reales de temperaturas, y de derecha a izquierda
las corrientes frías.
Figura 4
Dado que no es posible transferir energía a través del pinch, los intercambios de
energía deberían realizarse por arriba y por debajo del pinch. Por lo tanto, si queremos
mantener los requerimientos de servicios en su valor mínimo, debemos diseñar dos
RIC, una por arriba y una por debajo del pinch. En el caso que tuviéramos que transferir
una cierta cantidad de energía a través del pinch (intercambio entre una corriente
caliente por arriba y una fría por debajo del pinch), dicha energía no estaría disponible
para calentar las corrientes frías por arriba del pinch, y por lo tanto debería requerírsele
una energía adicional al servicio auxiliar de vapor (Servicio Caliente, SC). Lo mismo
ocurriría entre las corrientes frías y calientes por debajo del pinch, y una energía
10
adicional debería ser removida al servicio auxiliar de agua de enfriamiento (Servicio
Frío, SF).
En resumen cuando una cierta cantidad de energía fluye a través del pinch (RP > 0) la
energía requerida o transferida a los servicios se incrementará en la misma cantidad.
Aunque la metodología para diseñar la red la RIC (Cruzamiento de corrientes) la
veremos mas adelante, resulta ilustrativo en este momento proponer una RIC potencial
para el esquema de corrientes en estudio. De esta forma en figura 5 se muestra la red
propuesta, que consta de 7 intercambiadores, 4 por arriba del pinch y 3 por debajo.
Cada intercambiador se representa como una línea perpendicular que une las dos
corrientes que intercambian calor, con dos círculos igualmente numerados en los
extremos. Los intercambiadores entre corrientes de proceso y servicios se representan
mediante círculos sobre dichas corrientes con una H o una C según sea servicio
caliente o frío respectivamente.
Figura 5
Así puede observarse que la red interior esta constituida por 4 intercambiadores
(1,2,3,4), y la red auxiliar posee 3 intercambiadores, dos con el servicio caliente y uno
con el servicio frío. Las cargas calóricas transferidas en cada intercambiador se indican
con números de bajo de los círculos (Ej. intercambiador 1 transfiere una carga de 210).
Se muestran además las temperaturas de entrada y salida para cada intercambiador. A
11
partir de este diagrama se puede generar un esquema más explicito que nos muestra la
RIC en una forma mas aproximada a la que vemos en un flowsheet. Nos queda una
típica RIC integrada energéticamente como vemos en figura 6.
Figura 6
VIII.3 CRUZAMIENTO DE CORRIENTES CON SERVICIOS MÍNIMOS
Una vez calculados los requerimientos mínimos de servicios auxiliares, por lo general
se diseñan dos RIC, una por arriba y otra por debajo del pinch. Si bien existen varios
métodos para el diseño de las RIC, veremos a continuación solo uno de ellos. Veremos
el método propuesto por Linnhoff y Hindmarsh (1983), que pone énfasis en el
posicionamiento de los intercambiadores desde el pinch hacia afuera. Otro método es
del tipo algorítmico, y utiliza una técnica de Programación Mixta Entera Lineal. Fue
propuesto por Papoulias y Grossmann (1983-a) y su solución se encuentra a través de
GAMS. Este método se ve en cursos de posgrado.
Cruzamiento de Corrientes en el Pinch (Linnhoff y Hindmarsh):
En la aplicación de este método resulta de mucha ayuda el diagrama de la figura 4 en el
cual se muestran las corrientes de proceso (frías y calientes), separadas por el pinch,
que descompone el problema en dos. En el pinch las temperaturas de las corrientes
12
frías y calientes están separadas por el ∆Tmin que es la mínima aproximación de
temperaturas.
En figura 7 vemos esquemáticamente un intercambiador de calor en contracorriente
con las siguientes datos de corrientes:
Corriente
entra sale
m·Cp
Aproximación de T
Calor Transferido
Caliente
Thi
Tho
Ch
Extremo Caliente: ∆T2
Fría
Tci
Tco
Cc
Extremo Frío: ∆T1
Figura 7
Si realizamos un balance de energía para las dos corrientes, nos queda:
Q = C h Thi − Th0
(
)
o
Thi − Th0 =
Q
Ch
(6)
(
)
o
Tc0 − Tci =
Q
Cc
(7)
Q = C c Tc0 − Tci
restando ecuación 7 de 6, nos queda:
(T
hi
 1
1 

− Tc0 − Th0 − Tci = Q
−
 Ch C c 
) (
∆T2 − ∆T1 =
)
Q(C c − C h )
ChC c
(8)
(9)
13
Q
De acuerdo a la estrategia de Linnhoff, se considera luego la ubicación potencial de los
intercambiadores en el pinch que fija de manera arbitraria: Cuando un intercambiador
se posiciona en el lado caliente del pinch, ∆T1 = ∆Tmin y la ecuación 9 se transforma en:
∆T2 = ∆Tmin +
Q(C c − C h )
ChC c
(10)
Si analizamos la ecuación 10 veremos que para que ∆T2 ≥ ∆Tmin debe cumplirse que
Cc ≥ Ch , dado que Q > 0 y los valores de Cc y Ch son positivos. Por lo tanto para que un
cruzamiento de corrientes sea factible del lado caliente del pinch debe cumplirse como
condición que Cc ≥ Ch. En el caso contrario, el intercambiador no será factible debido a
que se verifica que: ∆T2 < ∆Tmin.
Para el lado frío del pinch el concepto es igual, tomándose ∆T2 = ∆Tmin y quedando la
ecuación 9 como:
∆T1 = ∆Tmin −
Q(C c − Ch )
ChC c
(11)
En este caso para asegurar que no exista violación en la aproximación de temperaturas
(∆T1 ≥ ∆Tmin) será necesario y suficiente que Ch ≥ Cc.. O sea la condición inversa que
para el lado caliente del pinch.
A modo de ejemplo vemos a continuación el cruzamiento de corrientes del lado caliente
del pinch, para un sistema de 4 corrientes, 2 calientes H1, H2 y dos frías C1, C2. Se
asume que la energía disponible es suficiente para los intercambios desde o hacia las
corrientes. Por ello en la figura 8(a) solo se muestran las corrientes y los valores de Ch
y Cc y no las temperaturas.
14
Figura 8
15
Dado que ∆Tp = ∆T1 = ∆Tmin , para asegurar que ∆T2 ≥ ∆Tmin será necesario que Cc ≥
Ch Por lo tanto los cruzamientos entre las corrientes H2 y C1 o C2 son factibles.
Además dado que CC2 – CH2 = 4 es mayor que CC1 – CH2 = 1, podríamos tentarnos y
establecer un cruzamiento entre H2 y C2 (figura 8(b). Sin embargo esto nos conduce a
un serio problema, ya que el cruce entre H1 y C1 es no-factible. Para salvar esta
situación es posible separar las corrientes H1 y C2 en dos corrientes paralelas como se
muestra en figura 8(c). La corriente H1 la separamos en dos corrientes paralelas
iguales (2 y 2) y C2 en una proporción 60% y 40%. Luego manteniendo el cruce H2 -C2
con el 60% de C2, generamos 2 nuevos cruces: 50% de H1 con C1 y 50 % de H1 con
40% de C2. El resultado es una red con tres intercambiadores en el pinch.
Resulta obvio que, si al comienzo hubiéramos establecido el cruce entre H2 y C1, el
cruce restante entre H1 y C2 era factible y por lo tanto tendríamos una red más simple
con solo dos intercambiadores como se ve en figura 8(d).
Para evitar la separación de corrientes y el uso adicional de intercambiadores, Linnhoff
y Hindmarsh proponen que los cruces del lado caliente del pinch solo sean
considerados cuando:
∆Cmatch < ∆Coverall
(12.a)
donde
∆Coverall = ∑ Cc i − ∑ Ch j
i
(12.b)
j
Debe notarse que el cruzamiento que intentamos en figura 8(b) viola la ecuación 12.a.
En cambio el cruce H2 – C1 de figura 8(c) satisface la mencionada ecuación. A tal fin
los autores proponen que el diseñador siga el algoritmo mostrado en figura 9 a fin de
posicionar los intercambiadores en el lado caliente del pinch.
16
Figura 9
La primera etapa del algoritmo es comprobar hasta que punto el numero de corrientes
calientes NH, es menor o igual al numero de corrientes frías NC. Si la respuesta es no,
separar una corriente fría y volver atrás. Esto se justifica debido a que si existen muy
pocas corrientes frías, luego de establecer NC cruzamientos nos quedan NH – NC
corrientes calientes sin utilizar en el pinch. Como no quedan corrientes frías disponibles
en el pinch, el remanente de corrientes calientes debe ser enfriadas mediante el servicio
frío. Luego, debido a que este servicio frío es usado para remover energía que no
puede ser removida por las corrientes frías, se requerirá una cantidad equivalente de
servicio caliente para calentar las corrientes frías. Esta se debe sumar a la cantidad
mínima de servicio caliente requerida en el lado caliente del pinch.
Cuando es necesario, las corrientes frías se separan hasta que NC = NH. Luego los
cruzamientos de corrientes se seleccionan de modo que: 1) Satisfagan los
requerimientos para cruzamientos en el pinch, o sea Cc ≥ Ch , y 2) satisfagan la
restricción 12. Cuando ello no es posible para todos los cruzamientos en el pinch, se
separa una nueva corriente fría y seleccionamos un nuevo conjunto de cruzamientos de
corrientes. Todo esto se aplica para los cruzamientos de corrientes en el lado caliente
del pinch.
17
Para los cruzamientos de corrientes en el lado frío del pinch, se aplica el algoritmo con
los siguientes cambios: en ecuación 12.b y en figura 9, Cc reemplaza a Ch (y viceversa),
NC reemplaza a NH (y viceversa), y las corrientes calientes son separadas cuando es
necesario.
Después de completar los cruzamientos sobre el lado frío o caliente del pinch, se
agregan intercambiadores adicionales sobre ambos lados para completar la red de
intercambiadores. Para esta última etapa, los autores no definen un procedimiento
sistemático como el anterior. Por ende, se debe tener mucho cuidado en esta etapa a
fin de evitar intercambiadores de calor no factibles debidos a violaciones en la
aproximación de temperaturas.
Ejemplo 2 (Linnhoff – Flowers, 1978.a,b)
Diseñar la RIC para las siguientes corrientes de proceso:
Corriente
Te (ºC)
Ts (ºC)
C (kW/ºC)
Q (kW)
C1
60
180
3
360
C2
30
130
2.6
260
H1
180
40
2
280
H2
150
40
4
440
Tome ∆Tmin = 10 ºC con las siguientes especificaciones:
Agua de enfriamiento (cw): Te = 30ºC, Ts ≤ 80ºC, costo de cw = 0.00015 $/kg
Vapor sat.(s): T = 258ºC, ∆Hv = 1676 kJ/kg, costo de s = 0.006 $/kg
Coeficientes globales de transferencia de calor:
Uheater = 1
kW / m2 .o C
Ucooler = Uexch = 0.75kW / m2 .o C
Costo de compra de los intercambiadores de calor:
18
Cp = 3000.A 0.5
($,m )
2
Operación de equipos = 8500 hr/año
Tasa de Retorno = r = 0.1
Solución:
Tomando un ∆Tmin = 10 ºC, se ajustan las temperaturas de las corrientes calientes, y se
calculan los requerimientos mínimos de servicios usando el método TI. Los valores
calculados se muestran en figura 10.
Corriente
Te (ºC)
Ts (ºC)
Te (ºC)
Ts (ºC)
Intervalo
C1
60
180
60
180
T4
T0
C2
30
130
30
130
T5
T3
H1
180
40
170
30
T1
T5
H2
150
40
140
30
T2
T5
Tabla de Temperaturas ajustadas
Luego de calculados los balances de energía para todos los intervalos vemos que Rp =
R2 = 0 y las temperaturas del pinch son 140º y 150º para las corrientes frías y calientes
respectivamente. Los requerimientos mínimos de calentamiento y enfriamiento son: 60
y 160 kW.
Examinamos ahora las corrientes por arriba y por debajo del pinch para determinar los
cruzamientos posibles (intercambiadores). Del lado caliente solo existe una posibilidad
de cruzar H1 y C1, ya que las otras corrientes no están presentes de ese lado (figura
11.a). Por debajo del pinch (lado frío) están presentes las cuatro corrientes, aunque
solamente H1, H2, y C1 están presentes en el pinch. C2 termina en 130º, o sea por
debajo de la temperatura del pinch (140º). Sin separación de corrientes, solo es factible
el cruzamiento de H2 – C1, debido a que CH2 > CC1, mientras que CH1 < CC1. Sin
embargo se debe tener cuidado de no transferir la totalidad de la energía requerida por
C1 (240 kW). Si se hace esto, el cruzamiento H1 – C2 es posible, aunque CH1 < CC2,
debido a que la corriente C2 no alcanza el pinch. Ya que para este intercambiador ∆T1
< ∆T2 y ∆T1 ≥ ∆Tmin = 10 ºC, solamente 86.58 kW pueden ser transferidos como se
19
muestra en figura 11.b. El remanente de la corriente C1 se calienta con vapor (173.42
kW), y dado que este calor no se toma de las corrientes calientes, la cantidad
equivalente de calor se debe remover de las corrientes calientes usando agua de
enfriamiento, que excede el requerimiento mínimo de servicio frío (160 kW).
Figura 10
Alternativamente, mucho menos calor se transfiere entre H2 y C1 (40 kW) y nos queda
sintetizada la red de la figura 11.c. Combinándola con la red por arriba del pinc, nos
queda una red con 6 intercambiadores interiores, un intercambiador para calentamiento
20
con vapor y uno para enfriamiento con agua (figura 11.d). Debe notarse que esta red
utiliza los requerimientos mínimos de servicios, pero incluye 8 intercambiadores, tres
por arriba del mínimo, según veremos mas adelante. La próxima etapa es considerar
las posibilidades de reducir los intercambiadores, mediante la remoción de los loops o
reciclos de calor.
Figura 11
21
VIII.4 MINIMO NUMERO DE INTERCAMBIADORES DE CALOR
Una vez diseñado una RIC que opera con los requerimientos mínimos de calentamiento
y enfriamiento, usando el método de Linnhoff y Hindmarsh (1983) ó el método
algorítmico de Papoulias y Grossmann (1983.a), es común reducir el numero de
intercambiadores de calor hacia un mínimo mientras se eleva el consumo de servicios,
particularmente cuando se pueden eliminar pequeños intercambiadores.
En esta forma se puede obtener un menor costo anualizado, especialmente cuando el
costo del combustible es bajo en relación al costo de compra de los intercambiadores.
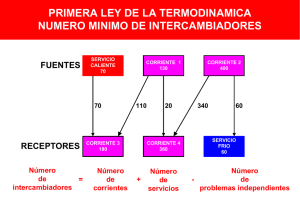
Antes de continuar es importante destacar que Hohmann (1971) descubrió que en
muchas circunstancias el Número Mínimo de Intercambiadores de Calor (NHX,min) en
una RIC es:
NHX,min = NS + NU − 1
(13)
donde NS es el número de corrientes y NU es el número total de servicios fríos y
calientes. Por lo tanto para los ejemplos anteriores con 4 corrientes, el NHX,min = 5.
En sus trabajos sobre integración calórica, Hohmann (1971) mostró que en una RIC
con NHX intercambiadores, existen NHX - NHX,min ciclos de calor. O sea que los ciclos
aparecen cuando él número de intercambiadores supera el valor mínimo. El ciclo de
calor más simple involucra el intercambio de calor entre dos corrientes en dos
intercambiadores separados. En forma más general, los ciclos de calor involucran el
intercambio de calor entre varias corrientes, digamos NS, usando el mismo número de
intercambiadores, NHX, tal que NHX = NS. Además, los ciclos de calor se abren
removiendo un intercambiador, y ajustando las cargas calóricas correspondientes,
hasta que NHX = NS – 1. Cuando esto se logra, es común que fluya calor a través del
pinch, y que los servicios se incrementen por arriba del mínimo, aunque esto no
siempre ocurre. Lo veremos a través de un ejemplo.
Ejemplo 3
Volviendo a la RIC de la figura 11.d que fue diseñado para minimizar los servicios fríos
y calientes, y que poseía 8 intercambiadores (tres mas que el valor mínimo para 4
corrientes, ecuación 13). Veamos como identificamos y removemos los ciclos de calor
uno por uno, analizando el impacto sobre el costo de capital, el costo de los servicios, y
el costo anualizado CA en ecuación 3.
22
Solución: A partir de la figura 11.d y usando las especificaciones del ejemplo 2, se
calcula el área de transferencia para cada intercambiador (Ecuación 2); se estima el
costo de compra usando CP = 3000 A0.5, dándonos un valor de 66900 $. El costo anual
de vapor y agua de enfriamiento es 10960 $/año . Luego combinado con el costo de
compra y multiplicado por la tasa de retorno, nos da CA = 17650 $/año.
Para eliminar el primer ciclo de calor entre las dos corrientes H1 y C1 (figura 12.a),
combinamos el intercambiador de 80 kW con el de 60 kW como se muestra en figura
12.b. Esta combinación causa una violación en la aproximación de temperaturas ya
que: (110ºC – 113.33ºC) = - 13.33ºC, que se debe eliminar transfiriendo menos calor (x)
en este intercambiador. Esta cantidad x se calcula de manera tal que ∆Tmin = 10ºC del
lado frío del intercambiador. O sea la temperatura de la corriente H1 se reduce a
123.33ºC. Luego por balance de calor:
140 − x = 2.(180 − 123.33)
Y la reducción en la carga calórica es x = 26.66 kW. Además para tener en cuenta esta
reducción, se debe incrementar el consumo de vapor en una cantidad x para calentar la
corriente C1 a 180ºC y las cargas de los otros 5 intercambiadores deben ser ajustadas
en la misma cantidad como se muestra en figura 12.c. Obviamente esto también incluye
el mismo incremento de agua de enfriamiento, debido a que x unidades de calor se
transfieren a través del pinch. Una vez ajustadas las cargas calóricas de los
intercambiadores, nos queda la red mostrada en figura 12.d. La Tabla 2 muestra que el
costo total de compra de los siete intercambiadores se reduce a 57470 $, pero el costo
de los servicios se incrementa a 13250 $/año, y luego CA se incrementa a 19000 $/año.
Para eliminar el segundo ciclo de calor en el cual se intercambia calor mediante dos
intercambiadores entre H2 y C1 (figura 12.d), se combina el intercambiador de 40 kW
con el de 120 kW (figura 12.e). Normalmente se mueve la carga más pequeña para
combinarla con la mas grande, a menos que ambas sean comparables como en el
primer ciclo. En este caso, dado que no existe violación de la aproximación de
temperaturas no es necesario ajustar las cargas de los intercambiadores. Luego en
tabla 2 el costo de los servicios no se modifica, y el costo total de compra se reduce a
54430 $, lo cual reduce el valor de CA a 18690 $/año.
23
El último ciclo de la red posee 4 intercambiadores que involucran a 4 corrientes (figura
12.e). Uno de ellos se puede eliminar desplazando la carga calórica del intercambiador
más chico alrededor del ciclo. Nos queda como consecuencia la red de figura 12.f,
aunque esta posee una violación en la aproximación de temperaturas (150 – 144.44) <
10ºC. Para eliminarla, se reduce la carga de 253.33 kW en una cantidad y de modo tal
que:
253.33 − y = 3.(140 − 60)
para permitir que la corriente C1 deje el intercambiador a 140ºC. Esta cantidad de calor
(y = 13.33 kw) debe ser suministrada y removida mediante una cantidad adicional de
vapor y de agua de enfriamiento respectivamente como se ve en figura 12.g, donde se
muestra la red de intercambiadores final, con solo cinco intercambiadores. Para esta
RIC en la Tabla 2, el costo total de compra se reduce a 45930 $, pero el costo de los
servicios se incrementa a 15340 $/año, resultando un mayor costo anualizado de CA =
19930 $/año.
Puede observarse que para este sistema, la RIC con 8 intercambiadores tiene un
menor CA cuando ∆Tmin = 10ºC. Por supuesto la relación de compromiso entre el costo
total de compra y el costo de los servicios cambia con la disminución del costo de los
combustibles y con el incremento del costo de capital o la tasa de retorno. Obviamente
para condiciones diferentes, el menor costo anualizado puede corresponder a otra
configuración.
24
Figura 12: Ruptura de ciclos de calor, a) 8 intercambiadores, primer ciclo; b) 7
intercambiadores, violación de ∆Tmin; c) 7 intercambiadores, desplazamiento de carga
calórica; d) 7 intercambiadores, segundo ciclo.
25
Figura 12:e) 6 intercambiadores, tercer ciclo; f) 5 intercambiadores, violación de ∆Tmin;
g) 5 intercambiadores.
Tabla 2: Comparación de costos
26
VIII.5 APROXIMACIÓN OPTIMA DE TEMPERATURA
Como ya hemos visto en items anteriores, la aproximación mínima de temperatura
∆Tmin posee fundamental importancia en el diseño de la RIC. Así hemos visto que en la
medida que ∆Tmin Æ 0 nos aproximamos al pinch verdadero con un área de
transferencia de calor que se aproxima a infinito, mientras que los requerimientos
mínimos de calentamiento y enfriamiento se aproximan al mínimo absoluto.
En el otro extremo cuando ∆TminÆ ∞ , el área de transferencia se aproxima a cero y los
requerimientos de servicios se incrementan hasta un máximo, que corresponde a un
intercambio de calor nulo entre corrientes de proceso. Este comportamiento de ∆Tmin,
área y requerimiento de servicios, se traduce en última instancia en variaciones en los
Costos de Operación y de Capital. En la figura 13 se grafica la variación de ambos
costos con ∆Tmin.
Figura 13
En ella observamos, que a medida que ∆Tmin se incrementa, el costo de capital se
reduce tendiendo a cero, paralelamente con la disminución del área de intercambio de
calor. En forma similar cuando disminuye el valor de ∆Tmin , el costo de servicios
(operación) disminuye linealmente hasta un valor umbral de diferencia de temperatura
27
∆Tthres, debajo del cual el costo de los servicios no se reduce. Además cuando ∆Tmin ≤
∆Tthres no existe punto pinch, y los compromisos entre costos de capital y servicios
cuando varia ∆Tmin no son aplicables. En resumen, cuando diseñamos una RIC, es
importante considerar el efecto de ∆Tmin.
VIII.6 BIBLIOGRAFÍA
Hohmann E. C., "Optimun Networks for Heat Exchnage", Ph. D. Thesis, Chemical
Engineering, University of Southhern California, Los Angeles, CA, 1971.
Linnhoff, B. "Use Pinch Analysis to Knock Down Capital Cost and Emissions", Chem.
Engn. Prog., Agosto (1994).
Linnhoff B. y J. R. Flower. "Synthesis of Heat Exchanger Networks". AIChE J , 24, 633
(1978).
Linnhoff B. y E. Hindsmarsh. "The Pinch Design Method for Heat Exchanger Networks",
Chem. Eng. Sci, 38, 5, 745-763 (1983).
Linnhoff B. y S. Paker. "Heat Exchanger Networks with Process Modifications", IchemE
IIth Annual Res Meeting, April, bath, U.K., 1984.
Linnhoff, B. y J.A. Turner. "Simple Concepts in Process Synthesis give Energy Savings
and Elegant Designs", the Chemical Engineer. pp 621-624, Octubre, 1980.
Linnhoff, B. y D.W. Townsend. "Designing Total Energy Systems", Chem. Engn. Prog.,
78, 7. 72-80 (1982).
Linnhoff, B., Townsend, D. W., Boland, D. Hewitt, G.F., Thomas, B.E.A., Guy, A.R.,
Marsland, R.H.; Flower, JR., Hill, J.C., Turner, J.A. y D. A. Reay. "User Guide on
Process Integration for the Efficient use of Energy", The Institute of Chemical Engineers,
London, 1982.
McCabe, W., and E. Thiele, “Graphical Design of Fractionating Towers”, Ind. Eng.
Chem., 17, 605 – 611 (1925)
Nishida, N., Y., A., Liu, and L. Lapidus, “ Studies in Chemical Process Design and
Synthesis: III. A Simple and Practical Approach to the Optimal Synthesis of Heat
Exchanger Networks”, AIChE J., 23, 77 – 93 (1977)
28
Nishida N., G. Stephanopoulos y A. W. Westerberg, "A Review of Process Synthesis",
AIChEJ, 27, 321 (1981).
Papoulias, S., an I.E. Grossmann, “A Structural Optimization Approach in Process
Synthesis – II: Heat Recovery Network”, Comp. Chem. Eng., 7, 707 (1983a).
Papoulias, S., and I.E. Grossmann, “A Structural Optimization Approach in Process
Synthesis – III: Total Processing Systems”, Comp. Chem. Eng., 7, 723 (1983b).
29