Navegación carta
Anuncio

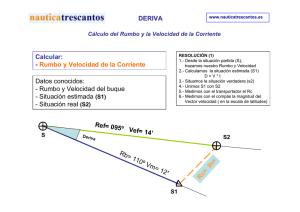
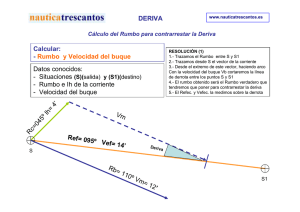
Navegación carta 4.1 CORRECCIÓN TOTAL. Cálculo de la Corrección Total a partir de la Declinación y el Desvío. Ya sabemos que el Norte puede ser: NORTE VERDADERO: Indicado por los meridianos geográficos o verdaderos. NORTE MAGNÉTICO: El marcado por una aguja náutica sin afectación de elementos magnéticos. NORTE DE AGUJA: El señalado por una aguja náutica afectada por elementos magnéticos. El ángulo que forman, en cada lugar y a cada rumbo del barco, el meridiano verdadero con el meridiano de aguja se denomina CORRECCIÓN TOTAL (Ct). Por tanto, la corrección total será la suma algebraica de la declinación magnética (dm) y el desvío () (suma teniendo en cuenta los signos de los sumandos). CORRECCIÓN TOTAL Para finalizar con lo relacionado con el magnetismo, no olvidemos que cualquier tipo de herramienta eléctrica, receptor de radio, micrófono, altavoz, equipos de navegación, circuitos eléctricos, móviles etc., alteran el campo magnético sobre la aguja compensada, si están próximos, apareciendo desvíos no compensados que falsearían la lectura. Cálculo de la Corrección Total a partir de la demora de aguja de una enfilación: Ya sabemos que una enfilación proporciona una demora verdadera. Por lo tanto, cuando la embarcación esté sobre la enfilación, si leemos el valor de ella y tomamos la demora de aguja de los objetos enfilados, la diferencia entre la demora observada y la proporcionada en la carta por la enfilación nos dará la corrección total. Recordemos que: Cálculo de la Corrección Total mediante el Azimut de aguja (Za) de la polar: Con este método podemos obtener una Corrección total bastante aproximada si nos acostumbramos a 1 calcular, a ojo, el azimut (Z) de la Polar; método del marino antiguo. Para ello observaremos la Polar y su 2 3 posición relativa con respecto a la línea que une las estrellas Alkaid y Cassiopea . Si esta línea es perpendicular al horizonte, la Polar estará por encima o por debajo del Polo Norte y su Zv = 0 = N. Si esta línea está horizontal y nuestra latitud es igual o menor de 50º el Zv = 1º E si Cassiopea está a la derecha de la Polar y Zv = 1º W si está a la izquierda. Si la latitud es mayor de 50º el valor del Zv = 2º. LINEA ALKAID-CASSIOPEA PARALELA AL HORIZONTE Menos aproximado sería decir siempre que el Zv(Polar) = 0º, aunque podría darse como bueno, pero sabiendo que cometemos un cierto error en el valor de la Corrección Total. Sólo como curiosidad, para obtenerla con exactitud deberíamos hallar el Zv(Polar) mediante el Almanaque Náutico entrando con el hl (horario del lugar de Aries) y la latitud, pero algunos de estos conceptos y, lógicamente, el procedimiento del cálculo, aún no se han visto ni entran en el programa de Patrón de Yate. 1 El Azimut es el arco de horizonte que va desde los puntos cardinales Norte o Sur hasta la vertical del astro. Hay varias clases de Azimut, según se cuente (Azimut Náutico, por cuadrantes y astronómico). 2 Es la última estrella de la cola de la constelación de la Osa Mayor. 3 La constelación de Cassiopea está formada por 5 estrellas que tienen forma de M (cuando está alta) o de W (cuando está baja). Sus estrellas no se observan casi nunca en la mar, residiendo su importancia en que la bisectriz de cualquiera de los dos ángulos que forma la constelación pasa aproximadamente por la Polar. 4.2 RUMBOS Y DISTANCIAS MEDIANTE RESOLUCIÓN GRÁFICA EN LA CARTA. Rumbo y distancia entre dos puntos, con y sin viento. Sin viento: Desde la situación del buque TRAZANDO EL RUMBO SIN VIENTO trazamos una línea hasta el punto de destino. Colocando el transportador como ya sabemos leeremos el rumbo que marca esta línea. Con viento: Podremos encontrarnos con que existe viento en la zona, entonces el rumbo leído sobre la carta será el rumbo de superficie (rumbo debido a la acción del viento) Rsf. En éste caso al Rsf. le aplicaremos el abatimiento, pero con signo contrario, y obtendremos el Rv. A partir de ese Rv, y conociendo la Ct, aplicaremos la fórmula ya estudiada para calcular el Ra, si fuera preciso. Recordemos que Abatimiento (Aº): Es el ángulo que forma la estela, es decir la derrota seguida por el barco, con la línea de crujía de éste. Al rumbo real que sigue el barco se le llama rumbo de superficie. A efecto de cálculos numéricos, cuando el abatimiento, es decir la acción del viento, haga que el barco abata a babor se considera negativo y cuando abata a estribor se considera positivo. Por tanto: RESOLUCIÓN ANALÍTICA Y GRÁFICA DEL CÁLCULO DEL Rsf Rumbo para pasar a una distancia de un punto de la costa, con y sin viento. Sin viento: Tendremos que hallar el rumbo verdadero que, desde la situación de salida, nos haga pasar a la distancia pedida de la costa. Para ello, marcaremos un arco de circunferencia de radio la distancia mínima y con centro en el punto de la costa en cuestión. Desde la situación de salida trazaremos una tangente a ese arco de circunferencia. Leemos con el transportador el rumbo obtenido que será el Rv. A partir de él se calculará el Ra como ya se sabe, si fuera necesario. Con viento: Si existe viento la línea tangente así trazada representará el Rsf que deberá seguir la embarcación para pasar a la distancia requerida. En éste caso al Rsf. le aplicaremos el abatimiento, pero con signo contrario, y obtendremos el Rv. A partir de ese Rv, y conociendo la Ct, aplicaremos la fórmula ya estudiada para calcular el Ra, si fuera preciso. Al igual que en el caso anterior, para resolver gráficamente éste cálculo, debemos tener en cuenta que el rumbo obtenido en la carta será el Rsf. Trazaremos el ángulo Aº en sentido contrario a su signo y, el rumbo así obtenido será el Rv. 4.3 LÍNEAS DE POSICIÓN: DISTANCIA RADAR A COSTA, ENFILACIÓN, OPOSICIÓN Y DEMORA. Situación mediante dos de las líneas de posición referidas, tomadas de manera simultánea: Tomaremos el valor de cada una de las líneas de posición, uno tras otro, y los trazaremos en la carta. El punto de corte de ambas será la situación del buque. 4.4 LÍNEAS DE POSICIÓN: DISTANCIA RADAR A COSTA, ENFILACIÓN, OPOSICIÓN Y DEMORA. Situación mediante dos de las líneas de posición referidas, tomadas de manera no simultanea: En éste caso trazaremos la primera línea de posición elegida. A continuación la trasladaremos por rumbo y velocidad y buscaremos cortarla con la segunda línea de posición tomada. A continuación se muestra el trazado gráfico en el caso haber tomado como líneas de posición una enfilación y una distancia radar. 4.5 CORRIENTE CONOCIDA (MEDIANTE RESOLUCIÓN GRÁFICA EN LA CARTA). Introducción: Al igual que el viento se define por su dirección y fuerza (que produce sobre el barco un abatimiento), las corrientes se definen por su rumbo e intensidad horaria, que origina en el barco una deriva. A la velocidad de la corriente se le denomina intensidad horaria y se expresa en millas por hora (nudos), de ahí lo de horaria, por lo que si la corriente actúa por dos horas su efecto sobre la velocidad del barco será el doble de 4 la intensidad horaria, si actúa por tres horas lo hace el triple y así sucesivamente . Al rumbo que realmente ha seguido el barco consecuencia de la acción de la corriente denomina rumbo efectivo (Ref) y a la velocidad la que se ha navegado, debido a la acción corriente, se le llama velocidad efectiva (Vef). como se le real a de la RUMBO Y VELOCIDAD EFECTIVOS Obviamente, la velocidad efectiva será mayor o menor que la velocidad debida a la máquina propulsora según que la corriente sea a favor o en contra del rumbo que hagamos. En el gráfico de al lado se representa esquemáticamente los conceptos anteriormente definidos. Conocido el rumbo y la intensidad horaria de la corriente, Hrb y situación de salida (o datos para obtenerla según el apartado 4.3 y 4.4), calcular gráficamente: 1. Ref y Vef, teniendo además como datos el Ra, Ct (o datos para calcularla) y la Vb. Para realizar el cálculo del Ref y la Vef, de manera gráfica, lo primero que debemos hacer es asegurarnos de que rumbo con el que vamos a trabajar es el Rv, es decir, si nos dan Ra lo convertiremos en Rv mediante el uso de la Ct pues ya sabemos que todo lo que se traza o se lee en la carta tiene que ser verdadero, no valen valores de rumbo o demoras de aguja. A continuación, y basándonos en el gráfico anexo, veamos la resolución del cálculo. 4 Tener en cuenta que la dirección del viento se define como el punto del horizonte de donde viene; en cambio la dirección de la corriente se define como el punto del horizonte hacia el que va, es decir por su rumbo. Realizaremos los cálculos necesarios para determinar la situación de salida, que en el gráfico hemos designado como punto 1, y una vez obtenido éste partimos de él con rumbo verdadero Rv y velocidad verdadera Vv, supuestos ambos constantes, y al cabo de 4 horas hemos estimado que nos encontramos en la situación 2 pero, al situarnos mediante cualquiera de los métodos conocidos, se obtiene como situación final verdadera la situación F. Esto se debe a la existencia de una corriente cuyo rumbo obtendremos uniendo los puntos correspondientes a la situación 2 y a la situación final (F) y su valor lo obtendremos leyéndolo con el transportador en la forma usual, y cuya intensidad horaria será la distancia entre estas dos situaciones Ic, que tomaremos con el compás y mediremos en la escala de latitudes, a la altura aproximada del lugar en que se realiza el cálculo como siempre, dividida por el número de horas 5 (H) que hemos navegado . EFECTO DE LA CORRIENTE SOBRE EL RUMBO Y VELOCIDAD DEL BUQUE Ic Ih = H Si ahora unimos el punto de salida 1 con el de llegada F obtendremos el Ref, rumbo que en realidad ha seguido el barco como consecuencia de la corriente, y la Vef cuyo valor está dado en función del número de horas navegadas H, por ello no debemos olvidar dividir el valor obtenido por H, al igual que se hizo con la Ic, para expresarla en Vef en una hora. 2. Ra y Vef, teniendo además como datos la situación de llegada (o datos para calcularla), Ct (o datos para calcularla) y la Vb. En esta resolución nos basaremos también en el gráfico anterior pero suponiendo que el tiempo navegado es de 1 hora y no de 4 como antes, aunque es conveniente que el alumno vaya trazando su propio gráfico, paso a paso, según sigue la explicación de la resolución gráfica que vamos a ver. Realizaremos los cálculos necesarios para determinar la situación de salida, que en el gráfico hemos designado como punto 1. Igualmente, realizaremos los cálculos necesarios para determinar la situación de llegada, que en el gráfico hemos designado como punto F. Uniendo ambos puntos obtenemos el Ref. Desde F trazamos el rumbo opuesto al rumbo de corriente (Rc) dado y sobre él marcamos la intensidad de la corriente dada, que si no nos dicen lo contrario, la tomaremos como Ih. Esto genera un punto, en el gráfico designado por 2. Por último, uniendo el 1 con el 2 obtendremos el Rv. Ahora sólo quedar hacer las operaciones y tomas de medidas necesarias para contestar a las preguntas pedidas (pasar el Rv a Ra, calcular el Ref, la Vef, hora de la llegada). Si la intensidad de la corriente dada no fuera la Ih, pues nos hubieran dado datos para saber el tiempo navegado, todas las velocidades que nos pidan calcular debemos dividirlas por ese tiempo navegado a fin de expresarlas en nudos (distancia navegada en una hora). 3. Ra y Vb, teniendo además como datos la situación y hora de la llegada. Como en el caso anterior, en esta resolución nos basaremos también en el mismo gráfico pero en éste caso el tiempo navegado nos lo dan como intervalo desde la hora de salida y la de llegada aunque es conveniente que el alumno vaya trazando su propio gráfico, paso a paso, según sigue la explicación de la resolución gráfica que vamos a ver. Comenzaremos realizando los cálculos necesarios para determinar las situaciones de salida y de llegada, que en el gráfico hemos designado como puntos 1 y F. Uniendo ambos puntos obtenemos el Ref. Desde F trazamos el rumbo opuesto al rumbo de corriente (Rc) dado y sobre él marcamos la intensidad de la corriente dada, que será Ih, multiplicada por el intervalo de tiempo transcurrido entre la hora de salida y la de llegada, que es el tiempo navegado. De esta forma generaremos el punto 2. Uniendo 1 y 2 obtendremos el Rv y la 5 Se recomienda repasar los conceptos y problemas realizados en el Curso de patrón de Embarcaciones de Recreo. distancia navegada en el intervalo de tiempo dado. Ahora sólo quedar hacer las operaciones y tomas de medidas necesarias para contestar a las preguntas pedidas (pasar el Rv a Ra, calcular el Ref, la Vef, Vb). 4.6 CORRIENTE DESCONOCIDA (MEDIANTE RESOLUCIÓN GRÁFICA EN LA CARTA). Calcular la corriente desconocida, su rumbo y la intensidad horaria, mediante una situación de salida obtenida según el apartado 4.3 y la situación estimada a la misma hora que la verdadera. En esta resolución no realizamos gráfico alguno sino que, por su simpleza, dejamos que el alumno vaya trazando su propio gráfico, paso a paso, según sigue la explicación de la resolución gráfica que vamos a ver. En primer lugar, realizaremos los cálculos necesarios para determinar la situación de salida, que en el gráfico hemos designado como punto 1. A continuación, marcaremos en la carta la situación estimada. Uniendo ambas posiciones obtendremos el Ref, que mediremos siempre desde la situación estimada a la verdadera, y la Vef, que será la distancia entre ambos puntos pero expresada en nudos. 4.7 SITUACIÓN DE ESTIMA (MEDIANTE RESOLUCIÓN GRÁFICA EN LA CARTA). Conocida la situación de salida y el rumbo de aguja. Estima gráfica, incluidos el viento y la corriente. En éste caso conoceremos la situación de salida (o datos para obtenerla), Ra, Ct (o datos para calcularla), la Vb, la dirección desde la que sopla el viento, el abatimiento que éste produce, la dirección hacia la que fluye la corriente (Rc) y la intensidad horaria de ella (Ih), y se nos pide realizar un cálculo estimado de la posición del barco, en un momento determinado, teniendo en cuenta la acción del viento y la de la corriente existentes. Vamos a ir resolviendo la cuestión paso por paso, anexando gráficos consecutivos de que cada uno de los trazos realizados. 1. Realizaremos los cálculos necesarios para determinar la situación de salida y la marcaremos en la carta. En el gráfico se le designa por A. 2. Realizaremos los cálculos necesarios para determinar el Rv al que se navega, la trazaremos en la carta a partir de A y sobre él marcaremos, con el compás, el valor de la Vb, lo que genera el punto B. 3. Desde B trazaremos el Rc y, sobre él con el compás, marcaremos el valor de la Ih. 4. Uniremos A y C obteniendo así el Ref y la Vef. 5. Por último, desde A o desde C, como en nuestro gráfico, aplicaremos al Ref el valor del abatimiento obteniendo así un Ref nuevo, al que hemos designado con Refn. Éste Refn es el rumbo que realmente hará el barco sometido a las acciones del viento y de la corriente. Hemos supuesto que el viento es del norte y produce un abatimiento de 15º. Es importante recordar que cuando se da la dirección del viento estamos diciendo “desde dónde viene el viento” (decir que hay viento norte indica que el viento viene del norte, o sea, los objetos abaten hacia el sur) mientras que al citar la corriente estamos diciendo “hacia dónde va la corriente” (decir que la corriente es sur indica que va hacia el sur, o sea, los objetos derivan hacia el sur). Es evidente que mediante esta resolución gráfica llegaríamos a obtener el Ref debido a viento y corriente, al que hemos llamado Refn, pero no podríamos saber la Vefn hasta que no hiciéramos una composición vectorial con los vectores Ref con su Vef y Vto con su velocidad del viento. 4.8 DERROTA LOXODROMICA: RESOLUCIÓN ANALÍTICA. Introducción Sabemos que se llama DERROTA al camino recorrido DERROTA LOXODROMICA. por el barco, sobre la superficie marítima del Globo, para trasladarse desde un punto a otro. La derrota puede ser LOXODRÓMICA y ORTODRÓMICA. A los efectos de este curso, estudiaremos algunos aspectos de la derrota LOXODRÓMICA. La derrota loxodrómica es la determinada por la curva que trazada en la esfera terrestre corta a todos los meridianos bajo el mismo ángulo, o sea que es de rumbo constante. En la carta mercatoriana queda representada por una línea recta. Por tanto, la DERROTA LOXODRÓMICA es aquella que hace el barco sin cambiar de rumbo, por lo que si la representamos sobre la esfera terrestre veremos que, esta derrota forma ángulos iguales con cada uno de los meridianos que atraviesa. También concluiremos, al representar la derrota loxodrómica sobre la superficie terrestre, que es una espiral que termina en los Polos (siempre que no se navegue con rumbo verdadero norte, sur, este u oeste), como vemos en la figura. A continuación vamos a calcular la fórmula que corresponde a esta curva. Para ello fijémonos en la figura siguiente en donde: ABC representa la curva loxodrómica, REPRESENTACION, EN CARTA MECATORIANA, DE LA que al ser trazada sobre carta DERROTA LOXODROMICA mercatoriana, aparece como una recta que forma ángulos iguales con los meridianos. R es el rumbo. Lo es la longitud en el punto que, la loxodrómica, corta al Ecuador. L es la longitud en el punto A. L1 es la longitud en el punto B, y 6 la y l’a son latitudes aumentadas de los puntos B y C. En la figura tenemos que: (1) L Lo XB En el triángulo BXA se cumple que: tgR XB XB la tgR la De donde sustituyendo en (1) el valor de XB, tendremos: L Lo la tgR Para obtener el rumbo exacto que debemos hacer para ir desde B a C, iríamos al triángulo CYB en donde se cumple que: (2) tgR YC L1 L L YB l´a la la La fórmula anterior nos permite calcular el rumbo loxodrómico entre dos puntos de coordenadas conocidas. La navegación de estima es el sistema de navegación basado en la apreciación de la situación del buque, calculada a partir de las coordenadas geográficas del punto de partida y de las distancias y rumbos verdaderos a que se ha navegado. Estos últimos datos se obtienen de corredera y aguja respectivamente. Cada parte de la estima en que se navega a rumbo fijo es un trozo de loxodrómica, por lo que la carta 6 Se llama latitud aumentada al valor analítico que toma la latitud en la proyección mercatoriana y que sirve para determinar la separación entre los paralelos. La tabla XLI de las Tablas Náuticas nos da su valor. mercatoriana es la más adecuada para resolver y representar los problemas que se planteen. En los casos en que se requiera una gran exactitud, o en los que no se disponga de carta, la navegación de estima se efectúa por procedimientos analíticos. La situación estimada es la que se obtiene al navegar por estima y representa el centro de un círculo probable cuyo radio depende de los errores cometidos en la navegación y de las causas externas que la hayan afectado. Definamos ahora tres conceptos en los que nos basaremos para realizar el cálculo de la estima, y que son: Diferencia en latitud. Diferencia en longitud. Apartamiento. DIFERENCIA EN LATITUD, APARTAMIENTO Y DIFERENCIA EN LONGITUD En la figura consideraremos que E es el punto de salida, H es el punto de llegada, D es la distancia que media entre ambos, R es el rumbo, EH es la loxodrómica que los une, EP es la diferencia en latitud que los separa y ∆L es la diferencia en longitud entre ellos. Si consideramos que el segmento de loxodrómica EH está dividido en un infinito número de partes, separadas, entonces, por una distancia infinitesimal dD y por cada una de esas partes trazamos el paralelo y meridiano correspondiente, se nos forman infinitos triángulos elementales, cuyos lados serán la distancia infinitesimal antes mencionada (dD), la diferencia en latitud, también infinitesimal (dl) y un arco infinitesimal de paralelo que denominamos (da). Estos triángulos se podrán considerar planos (gráfico siguiente) y en ellos se podrá establecer que: TRIANGULO ELEMENTAL DE ESTIMA da dD senR da dl tgR dl dD cos R Fórmulas que integradas dan: l D cos R A D senR A l tgR Conviniendo en llamar APARTAMIENTO (A) a la suma de todos los catetos elementales situados sobre todos los infinitos paralelos trazados. Para obtener el valor del incremento en longitud, ΔL, ERROR ASUMIBLE AL SUPONER EL APARTAMIENTO vamos a suponer que el valor obtenido para A, IGUAL AL ARCO DE PARALELO DE LATITUD MEDIA apartamiento, es igual al tamaño del arco de paralelo de latitud media entre E y H. Esta suposición es bastante exacta pues la primera mitad del arco, EM, es menor que la suma de los apartamientos diferenciales a que sustituye, mientras que la segunda mitad, MH, es mayor, compensándose así las diferencias. Establecido lo anterior se puede decir que un arco de ecuador es igual al correspondiente de paralelo multiplicado por la secante de la latitud: L A sec lm En caso de que éste valor se quiera calcular con total exactitud debemos utilizar la fórmula derivada de la ecuación (2): L la tgR Para los signos de l, Δl, L, ΔL y A se tendrá en cuenta que los nombres y sentidos hacia el Norte y Oeste se consideran positivos y los Sur y Este negativos. RUMBO DIRECTO Y DISTANCIA DIRECTA Problema directo. Su propio nombre nos da una idea de su significado. Basta unir, en la carta mercatoriana, mediante una línea, las situaciones inicial y final y, a continuación, leer con el transportador el rumbo que marca dicha línea. Ése será el rumbo directo para ir de un punto al otro. Posteriormente, con el compás, tomamos la longitud del segmento entre la situación inicial y la final y, leyéndola sobre la escala de latitudes, obtendremos la distancia directa. Dicho de otro modo, si unimos ambas situaciones con una línea, el ángulo que forma esta con los meridianos será el RUMBO DIRECTO y la DISTANCIA DIRECTA será la separación existentes entre ambas situaciones, sobre esa línea. La realización de la estima de forma analítica consiste en obtener las coordenas de la situación de llegada mediante la adición, a las coordenadas de la situación de salida, de los incrementos, o decrementos, de longitud y latitud experimentados en la navegación. Éste cálculo se puede realizar mediante las Tablas Náuticas (método marino por excelencia) o mediante calculadora (método más cómodo pero sin ningún sabor marinero). Vamos a estudiar el MÉTODO MEDIANTE CALCULADORA (aplicando las fórmulas obtenidas en epígrafes anteriores) y teniendo en cuenta que según el modelo de calculadora que se use este proceso puede variar: Introducimos el rumbo y pulsaremos “cos”, a continuación, x (multiplicar) e introducimos la distancia navegada. El resultado así obtenido será la diferencia en latitud. Introducimos, de nuevo, el rumbo y pulsamos “sen” luego x (multiplicar) y despues introducimos la distancia navegada. Ahora hemos obtenido el apartamiento. Aplicamos la diferencia de latitud a la latitud de salida, teniendo en cuenta que si son de igual signo, o sea hacia el mismo hemisferio, las sumaremos, y en caso contrario las restaremos, y obtendremos la latitud de llegada. Sumamos latitud de salida y de llegada y dividimos por 2 obteniendo la latitud media. 7 Introducimos la latitud media y pulsamos “cos” y, a continuacion, pulsamos la tecla marcada “1/x” . De esta forma obtenemos la secante de la latitud media que pasamos a multiplicar por el apartamiento, antes obtenido, y así tendremos la diferencia en longitud. La diferencia en longitud tiene siempre el mismo signo que el apartamiento. Aplicamos la diferencia en longitud a la longitud de la situacion inicial, teniendo en cuenta que si son del mismo nombre se suman y si sn de distinto nombre se restan, y obtenemos la longitud de 8 llegada . En caso de que la estima la realicemos en función de varios rumbos y distancias debemos hallar los APARTAMIENTOS y DIFERENCIAS EN LATITUD de cada uno de ellos. Una vez obtenidos todos los sumaríamos, teniendo presente la regla de los signos antes citada, calculando así un apartamiento total y una diferencia en latitud total, que serán los que empleemos para obtener la latitud y longitud de llegada, siguiendo el mismo proceso que antes desarrollamos. A este tipo de estima se le llama PROBLEMA DIRECTO. Así explicado puede parecer algo engorroso, pero vamos a verlo con un caso práctico cuya comprensión va a resultar más fácil. Partiendo de l = 35º 23’ N y L = 005º 25’ W navegamos al 255º/v durante 45 minutos, en ese momento cambiamos al 260º/v y continuamos así durante 75 minutos, instante en el que cambiamos el rumbo, de nuevo, al 275º/v. Calcular la situación estimada una hora después del último cambio de rumbo, suponiendo que hemos mantenido una velocidad constante de 8 nudos. Sabemos que l D cos R y que A D senR Con estas fórmulas vamos a calcular los diferentes valores de Δl y A para cada uno de los rumbos. Para ello podemos confeccionar una tabla similar a la siguiente: 7 La secante (sec) es la inversa del coseno (cos) Las latitudes Norte son positivas, las latitudes Sur son negativas. La latitud de llegada será la latitud de salida más el incremento o menos el decremento en latitud que se produzca en función del rumbo al que navegamos. Las longitudes Oeste son positivas, las longitudes Este son negativas. La longitud de llegada será igual a la longitud de salida más el incremento o menos el decremento en longitud que se produzca en función del rumbo al que navegamos. 8 DIFERENCIA EN LATITUD - Δl N S RUMBO RUMBO CUADRANTAL DISTANCIA APARTAMIENTO - A E W 255 S75W 6 1,55 5,8 260 S80W 10 1,73 9,84 275 N85W 8 0,69 7 Δl = 1,55 + 1,73 - 0,69 = 2,59 S A continuación calculamos el apartamiento y el valor de la latitud media para obtener el ΔL. A = 5,8 + 9,84 + 7,97 = 23,61 W Con ellos hallaremos el lmedia L A sec lm y : linicial lfinal 35º 21,7´N 2 L A sec lm 28,9´W Una vez obtenidos Δl y ΔL los aplicamos a la latitud y longitud iniciales y obtendremos los finales linicial 35º 23,00´N l lfinal 35º 20,41´N 2,59´S Linicial 005º 25,00´W L 28,90´W Lfinal 005º53,90´W lfinal 35º 20,41´N Lfinal 005º53,9´W Problema inverso: El PROBLEMA INVERSO consiste en obtener, a partir de las situaciones de salida y llegada, el rumbo y la distancia navegada,es decir el RUMBO DIRECTO y la DISTANCIA DIRECTA. Para la resolución de este problema vamos, también, a contemplar el método con calculadora, teniendo en cuenta que según el modelo de calculadora que se use este proceso puede variar Hallamos el Δl e ΔL, restando algebráicamente las latitudes y longitudes finales e iniciales, así como la latitud media (como media aritmética de las latitudes inicial y final). Los siguientes pasos serán la aplicación de las fórmulas aprendidas en epígrafes anteriores: Hallaremos el apartamiento multiplicando el ΔL por el cos de la latitud media, como se desprende de las fórmulas siguiente: L A sec lm A L cos lm Con el apartamiento y el incremento en latitud obtenemos la tangente del rumbo, cuya función inversa (arctg) nos proporciona el rumbo. A l tgR tgR A l Obtenido el rumbo, podemos calcular la distancia por alguna de las dos siguientes fórmulas: l D cos R D l l sec R cos R A D senR D A A cos cR senR Veamos un cálculo númerico que nos ayudará a comprender mejor el procedimiento a seguir. Calcular Rumbo Directo y Distancia Directa para ir desde una situación de l = 36º 23,5’ N y L= 005º 27,0’ W a otra de coordenadas l = 35º 55´N y L = 005º 23,6’ W. En primer lugar hallaremos los incrementos de l y L (que convertiremos siempre en minutos de grado): lfinal 36º55,0´N linicial 36º 23,5´N Lfinal 005º 23,6´W Linicial 005º 27,0´W l L 31,5´N 3,4´E A continuación hallamos la latitud media: lm linicial lfinal 36º39,25´N 2 Sabemos que: L A sec lm A L cos lm A 3,4 cos(36º39,25´) 2,73´E Por otro lado, de la fórmula: A l tgR tgR A l obtenemos : tgR A 2,73 0,0866666 l 31,5 luego: R arctg (0.086666) tg 1 (0.086666) 4,95º Rumbo que obtenemos en cuadrantales y que tendrá los mismos nombres que Δl y A. Como el incremento en latitud era hacia el Norte y el Apartamiento hacia el Este, el rumbo será N 5 E = 005º. Una vez hallado el rumbo, la distancia la podemos obtener de cualquiera de las fórmulas de incremento en latitud o de apartamiento: l D cos R D l En nuestro caso: cos R l sec R D 31,5 sec 5º 31,6 millas Por tanto: Rdirecto N5º E Ddirecta 31.6 millas 4.8 MAREAS. Cálculo de la sonda en un momento cualquiera, momento directo e inverso (se preguntará como cuestión independiente de los ejercicios de navegación) Problema directo. Consiste en calcular la sonda en un lugar y momento determinados. La mejor manera de verlo es mediante un ejemplo numérico. Hallar la sonda a las 1200 horas locales en un lugar donde la carta marca 3 metros en el puerto de Cádiz, el 15 de Marzo de 2001. En principio, no olvidemos nunca que las horas del Anuario de Mareas son horas UTC, por lo que a las horas locales habrá que aplicarle el adelanto, o atraso vigente, para pasarlas a UTC. 1200 – 0100 = 1100 UTC A continuación entramos con la hora UTC en el Anuario, en el puerto citado, en la página correspondiente al mes del que se trata. Dentro de ese mes iremos a la fecha del HcGplea 0617 Alt 3,05 mts cálculo y buscaremos las horas de bajamar y la pleamar entre las que se encuentre la hora del enunciado (una HcGbaja 1208 Alt 1,20 mts vez pasada a UTC) y la altura de la marea a esas horas. En nuestro caso: Duración 0551 Apl 1,85 mts Siendo HcGplea la hora UTC de la pleamar, HcGbaja la hora UTC de la bajamar, Duración la duración de la creciente o la vaciante, Alt la altura de la pleamar y la bajamar y Apl la amplitud de la marea, diferencia entre las alturas de la pleamar y la bajamar. Hallaremos, a continuación, el intervalo entre la hora para la cual queremos hallar la sonda y la hora de la bajamar más próxima. HcGbaja 1208 HcGdada 1100 Intervalo 0108 Con estos resultados entramos, de nuevo, en el Anuario de Mareas en la Tabla denominada “Tabla para calcular la altura de marea en un instante cualquiera”. En ella, y en la parte correspondiente a “Duración de la creciente o vaciante” buscamos el valor más próximo al obtenido (0551), en este caso el valor más próximo en el Anuario es 0545; bajamos por esa columna hasta encontrar, en el apartado “Intervalo desde/hasta la bajamar más próxima”, el valor más próximo al del intervalo calculado (0108), en este caso el valor más próximo en el Anuario es 0109. Ahora nos desplazamos hacia la derecha en esa fila hasta llegar a la columna donde se encuentre la amplitud de marea más próxima a la hallada (1,85 mts), en este caso 0200. Bajamos por esta columna hasta coincidir con la fila por la que antes nos desplazamos y obtendremos así un valor de “Corrección aditiva a la altura de la bajamar más próxima” que en nuestro caso es 0,19. Veamos, mediante un gráfico, el camino a seguir dentro de esta tabla. MODO DE DESPLAZARSE, A TRAVÉS DE LA TABLA PARA CALCULAR LA ALTURA DE MAREA EN UN INSTANTE CUALQUIERA, PARA HALLAR EL VALOR DE LA CORRECCION ADITIVA A LA ALTURA DE LA BAJAMAR MÁS PROXIMA Una vez hallado el valor de la corrección, tendremos: Sm Sc Altbaja Con En nuestro caso será: En donde: Sm = sonda medida a la hora objeto del cálculo Sc = sonda carta Altbaja = altura de la bajamar más próxima Con = corrección Sm 3 1,20 0,19 4,39 mts Problema inverso. Consiste en calcular las horas en las mareas entrante y vaciante entre las cuales tendremos una sonda igual o mayor que la deseada. Igualmente, recurrimos al cálculo numérico para su mejor comprensión. El día 15 de Marzo de 2001 una embarcación, que tiene de calado medio 1,35 mts., quiere entrar en Puerto América (Cádiz), con 3 mts. de agua bajo la quilla, por un lugar de sonda 2 mts. ¿Con qué período de tiempo contará para hacerlo? Para la resolución de este caso tomaremos hora y altura de pleamares y bajamares y las amplitudes de ellas. HcG1ª plea 0617 HcG1ª baja 1208 Alt 3,05 mts Alt 1,20 mts Duración 0551 Apl 1,85 mts Ahora calculamos la sonda que necesitamos tener en el momento de recalar en puerto, según el enunciado. Calado 1,35 mts Agua bajo la quilla 3,00 mts Sonda necesaria 4,45 mts Sabemos que: Luego: Sbajamar Sc Altbaja Sc 2,00 mts Altbaja 1,20 mts Sbajamar 3,20 mts Sabiendo la Sbajamar y la Sonda necesaria (Sm) tendremos la Corrección aditiva a la altura de la bajamar más próxima: Sm Sbajamar Con Sm 4,45 mts Sbajamar 3,20 mts Con 1,25 mts Entramos en las tablas denominadas “Tabla para calcular la altura de la marea en un instante cualquiera” en la columna correspondiente a “Amplitud de la marea”, y buscamos el valor más próximo al que tenemos (1,85 mts.), en este caso 2,00 mts. En esta columna buscamos el valor más aproximado de la “Corrección aditiva” obtenida (1,25), que en este caso es 1,21 mts. Por esa fila nos desplazamos hacia la izquierda hasta que coincidamos con la columna de “Duración de la creciente o vaciante” más próxima a la que nos ocupa (0551) que es 0545, y en la intersección de esta columna con aquella fila leemos el valor del “Intervalo desde/hasta la bajamar más próxima” que será 0315. MODO DE DESPLAZARSE A TRAVES DE LA TABLA PARA CALCULAR LA ALTURA DE MAREA EN UN INSTANTE CUALQUIERA, PARA OBTENER EL VALOR DEL INTERVALO DESDE/HASTA LA BAJAMAR MÁS PROXIMA En el gráfico vemos el desplazamiento realizado a través de la citada tabla. Este será el intervalo que hay que sumarle a la hora de la bajamar más próxima para obtener la hora en que se medirá la sonda requerida. HcGbaja Intervalo 1208 0315 HcGpedida 1546 Aplicamos adelanto/atraso vigente y obtenemos la hora del lugar: HcG Ho O Ho HcG O 1546 0100 1646 Esta será la hora del comienzo del período durante el cual la sonda del lugar será la requerida. Para calcular la hora del final de dicho período tendremos que trabajar con la siguiente bajamar del día o, en caso de que en la fecha del cálculo sólo coincidiera una bajamar, con la primera bajamar del día siguiente, como es el caso que nos ocupa. HcG 2ª plea 1838 Alt 2,91 mts (16 / 03 / 01) HcG1ª baja 0033 Alt 1,26 mts Duración 0555 Apl 1,65 mts La Sonda necesaria = 4,45 mts. Al igual que antes calculamos la Sonda de la Bajamar y la Corrección aditiva. Sc 2,00 mts Sm 4,46 mts Altbaja 1,26 mts Sbajamar 3,26 mts Sbajamar 3,26 mts Con 1,20 mts A continuación calculamos el Intervalo de igual modo que antes. En la “Tabla para calcular la altura de marea para un instante cualquiera” entramos en la columna de la “Amplitud de marea” con el valor más próximo al obtenido (1,65) que es 1,50 mts., y buscamos, en ella, el valor más aproximado a la “Corrección aditiva” que tenemos (1,2 mts.) la cual es 1,19 mts. Nos desplazamos en esta fila hacia la izquierda hasta coincidir con la columna del valor obtenido para la “Duración de la creciente o vaciante” (0555), que será 0545 y, en la intersección de esta columna con aquella fila de la Corrección aditiva, leemos el valor del Intervalo que será, en este caso, 0400. Este valor habrá que restarlo a la hora de la bajamar utilizada, ya que la marea es vaciante, por lo que la sonda irá disminuyendo y, por tanto, a menor hora mayor sonda. HcGbaja Intervalo 0033(16 / 03 / 01) 0400 HcGpedida 2033(15 / 03 / 01) Aplicamos adelanto/atraso vigente y obtendremos hora del lugar: HcG Ho O Ho HcG O 2033 0100 2133 Luego el período de tiempo durante el cual la embarcación podrá recalar en Puerto América, bajo las condiciones requeridas será: Desde las 16 46 hasta las 21 33 del día 15 de Marzo de 2001