Prof.: Guillermo Corbacho C.

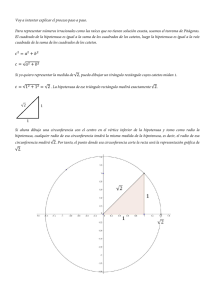
Prof.: Guillermo Corbacho C.
gcorbach@uc.cl
INTRODUCCIÓN
El presente trabajo es una recopilación en su muy amplia mayoría, de ejercicios PSU
propuestos –de los cuáles muchas veces el alumno se desazona por el hecho de no saber
resolverlos. Es por ello que nace la idea de comentar por escrito el desarrollo y solución de
los ejercicios. De este modo se pretende ayudar a internalizar los contenidos que van
participando en cada solución.
Este trabajo está ideado también para ser consultado por profesores, dado que, según mi
experiencia, la preparación universitaria ha sido más orientada a las matemáticas superiores
en lugar de las necesidades prácticas de la educación básica y media. Como serían estas el
de trabajar directamente en sus contenidos, elaborando guías e instrumentos de evaluación,
ya desde los primeros semestres de la carrera, de manera conjunta y graduada con los
estudios superiores.
Para su presentación, he subdividido los ejercicios según su enunciado en los siguientes
ítems:
I. Relaciones de Semejanzas
II. Teoremas de Euclides
ii. 1. Referido a la altura.
ii. 2. Referido a los catetos.
ii. 3. Ejercicios combinados referidos a la altura como a los catetos.
III. Teorema Particular de Pitágoras
iii. 1. Tríos Pitagóricos.
iii. 2. Teorema Particular de Pitágoras.
IV. Ejercicios combinados de Euclides con Pitágoras.
Parinacota, Quilicura.2009
1
Prof.: Guillermo Corbacho C.
I. Relaciones de semejanzas
1. Si en un ∆ABC rectángulo en C, se traza la altura hC . Podemos afirmar que siempre se
forman:
A) 3 ∆s semejantes.
B) 2 ∆s congruentes.
C) 2 ∆s semejantes.
D) 3 ∆s equivalentes.
E) 2 ∆s equivalentes.
Solución:
Sea ∆ABC rectángulo en C, tal como se muestra en la figura.
Siempre definirá tres Δs semejantes entre sí:
∆ABC ∼ ∆ADC ∼ ΔDBC
Alternativa A).
2. En la siguiente fig. el triángulo ABC es escaleno –con sus tres ángulos interiores de
distinta medida - y rectángulo en C, ¿Cuál(es) de las siguientes proposición(es) es (son)
verdadera(s)?
I. ACD = ABC
II. ∆ BCD ∼ ∆ ABC
III. ∆ ADC ∼ ∆ ABC
A) Solo I
B) I y II
C) I y III
D) I, II y III
E) Ninguna de las anteriores.
Solución:
ƒ Al bajar la altura desde el ángulo recto hasta la hipotenusa, siempre se definen dos Δs
más pequeños que son semejantes cada uno, con el original y entre sí. Por lo que, II. y
III. son verdaderas.
ƒ Además, siempre se forman las relaciones entre
ángulos que se muestran en la figura de la derecha.
Por lo tanto, I es también cierta.
Alternativa D).
3. En el ΔABC, rectángulo en C, se afirma que:
BC AB
I. ΔACD∼ ΔABC
II.
=
BD BC
De estas afirmaciones es (son) verdadera(s):
A) Solo I
B) Solo II
C) Solo III
D) I y II
E) Todas.
III.
AD CD
=
CD AB
Solución:
Analicemos I, II y III.
I. La altura bajada desde el ángulo rectángulo define solo Δs semejantes.
Por lo tanto, I es verdadera.
II. Ambas razones comparan en los triángulos ΔBCD y ΔABC a su respectiva
hipotenusa con el menor de sus catetos. Por lo tanto, II es una proporción
verdadera.
III. La razón de la izquierda compara al mayor de los catetos, con el menor en el ΔACD,
mientras que la razón de la derecha compara en el ΔABC a su altura con la
hipotenusa. No hay una correspondencia de lados homólogos. Por lo tanto, III es
falsa.
Así, solo son verdaderas I y II.
Alternativa D).
Parinacota, Quilicura.2009
2
Prof.: Guillermo Corbacho C.
4. De acuerdo con la figura se afirma que:
I. b:c = h:a
II. a:b = h:q
De estas afirmaciones es (son) verdadera(s):
A) Solo I
B) Solo II
C) Solo III
D) I y II
E) Todas.
III. b:h = h:q
Solución:
Analicemos I, II y III.
I. b:c = h:a
En los Δs rectángulos ABC y DBC se comparan respectivamente al
menor de su catetos con sus respectivas hipotenusas. Hay una comparación de lados
homólogos, de lados similares. Por lo tanto, I es una afirmación verdadera.
II. a:b = h:q En el ΔABC se compara al mayor de los catetos con el menor, mientras
que en el ΔDBC, rectángulo en D, se hace una comparación al revés, esto es, el
menor de los catetos respecto al mayor. Por lo tanto, la igualdad no es una
comparación de lados homólogos, no es verdadera. II. ES FALSA.
III. b:h = h:q El lado izquierdo de la igualdad, es una comparación en el ΔACD, entre
su hipotenusa con el mayor de sus catetos. Mientras que la igualdad del lado
derecho es una comparación en el ΔBCD, entre dos catetos, el menor respecto al
mayor. Así que no es una comparación de lados homólogos o similares. Por lo tanto,
la igualdad no es una afirmación verdadera. III. ES FALSA.
Luego, solo I es verdadera.
Alternativa A).
5. En el ΔABC, rectángulo en C, CD = hC ; CM = tC ; entonces β mide:
A) 20º
B) 110º
C) 55º
D) 70º
E) 32,5º
Solución:
Podemos completar la figura si tenemos presente que la suma de los
todo Δ es igual a 180º
CM = tC transversal de gravedad, se tiene entonces que M es
punto medio no sólo de la hipotenusa, sino también de la
circunferencia al cual el triángulo está inscrito. Ello se debe a que
toda hipotenusa logra coincidir con el diámetro de una
circunferencia, teniendo a su punto medio como centro de tal ⊗.
Por lo tanto, CM = tC = R, donde R es radio de la ⊗ . MB
también es radio de de la ⊗ y los radios definen dos lados
iguales sobre el ΔMBC, siendo este isósceles.
⇒ MCB = β por ser basal.
Por otra parte, la altura bajada desde el vértice C define triángulos.
Donde:
ACD = ABC = β
y del ángulo recto del vértice C, tenemos:
β + 25º +β = 90º
2 β + 25º = 90º
2 β = 90º −25º
2β = 65º
β = 32, 5º
Alternativa E)
Parinacota, Quilicura.2009
s interiores de
3
Prof.: Guillermo Corbacho C.
6. En la figura se tiene AB = 25, BC = AC = 15. Entonces hc = ?
A) 15
15
B)
2
15
C)
25
D) 9
E) 12
Solución
Usando
ab
c
Se tiene, al reemplazar valores :
hc =
=
15•15 3• 5 •3• 5
=
=9
25
5•5
Alternativa D)
7. En el triángulo ABC, rectángulo en C, CD es altura; β = 40º y AE bisectriz del
CAB. ¿Cuál es la medida del CFA?
A) 155º
B) 140º
C) 130º
D) 120º
E) 115º
Solución:
Como los ángulos agudos en un Δ rectángulo son siempre complementarios, se tiene, en
el ΔABC, rectángulo en C, que:
α = CAB = 50º.
Como AE es bisectriz del CAB = 50º ⇒ EAD = 25º
En el ΔADF, rectángulo en D y con los ángulos agudos complementarios, tenemos que,
el ángulo AFD = 65º
Y por último, ángulos adyacentes son suplementarios ⇒ AFD + CFA = 180º
65º + CFA = 180º
⇒
CFA = 180º −65º= 115º
Alternativa E).
Parinacota, Quilicura.2009
4
Prof.: Guillermo Corbacho C.
II. Teoremas de Euclides
II.1. Teorema de Euclides referido a la altura
8. En el triángulo rectángulo en C, siempre se cumple que:
A) hc = BD
B) hc = AD + BD
C) hc = AD • BD
D) hc 2 = AC 2 + BC 2
E) hc2 = AD • DB
Solución:
hc2 = AD • DB
Es conocido como el teorema de Euclides referido a la altura, para todo triángulo
rectángulo.
Alternativa E).
9. El triángulo ABC es rectángulo en C, entonces, siempre se cumple que p • q =
A) AC + BC
B) AC • BC
C) CD
2
D) CD
E) 2CD
Solución:
Se trata del teorema de Euclides relativo a la altura p • q = hc
Alternativa D)
10. Con los datos que aparecen en el triángulo. ¿Cuál es la medida de hc?
A) 36 [cm]
B) 9 [cm]
C) 6 [cm]
D) 3 [cm]
E) 2 [cm]
Solución:
Por Euclides relativo a la altura:
hc2 = pq = 9 • 4 = 36 ⇒ hc = 6 [cm]
Alternativa C).
11. Determina cuál(es) de los triángulos de la figura es(son) rectángulos:
A) Solo I.
B) I y II.
C) II y III
D) I y III
E) Todas.
Solución:
En cada uno de los triángulos I, II y III nos dan la altura hc y las proyecciones p y q de los
catetos sobre la hipotenusa. Ellos son elementos para aplicar el teo. de Euclides relativo a
la altura: hc2 = pq
Si los Δs fuesen rectángulos, deben verificar dicho teorema. Haciendo el cálculo mental,
notamos que solo II y III lo satisfacen.
Alternativa C).
Parinacota, Quilicura.2009
5
Prof.: Guillermo Corbacho C.
12. AB es diámetro de la semicircunferencia ACB. La medida de MC , sabiendo que
AM = 2 [cm] , MB = 3 [cm] y MC ⊥ AB , es:
A)
2 [cm]
B)
3 [cm]
C) 6 [cm]
D)
6 [cm]
E) No se puede determinar.
Solución:
Hay que recordar que todo ángulo inscrito que subtiende el
diámetro de una circunferencia es recto. Como se muestra en la
figura de la derecha.
Se define así un triángulo rectángulo del cuál CM es su altura. Como tenemos las
medidas de las proyecciones que ella define sobre la hipotenusa, aplicamos el teorema de
Euclides relativo a la altura:
MC2 = AM•MB
h 2 = 2•3⎫⎪
⎬ ⇒ hc = MC = 6 [cm]
= 6 ⎭⎪
Alternativa D).
13. En el ∆ABC rectángulo en A, de la figura adjunta; CD ⊥ AD. Entonces, CD mide:
A) 25
B) 144
65
C)
12
25
D)
12
E) 60
Solución:
En el triángulo rectángulo ABD, los números 12 y 13 forman parte de un trío
fundamental Pitagórico junto al 5. Así, AD = 5 .
Siendo además AD altura del triángulo ABC y CD es proyección del lado b sobre la
hipotenusa.
Por lo tanto, por teorema de Euclides relativo a la altura –que implica a las proyecciones
que delimita sobre la hipotenusa, se tiene:
h a2 = CD•DB
Alternativa D).
Parinacota, Quilicura.2009
52 = CD•12
25
= CD
12
6
Prof.: Guillermo Corbacho C.
14. En el triángulo MPQ se tiene que PS = MS = SQ. Además
entonces la medida del PSM es :
A) 100°
B) 90°
C) 80°
D) 70°
E) 60°
Solución:
PMQ + PQM = 90° ⇒
de los int. igual a 180º)
PMQ +
PQM = 90°,
MPQ = 90º (suma
Luego, el triángulo MQP es rectángulo en P, con
MQ hipotenusa. Los datos quedan representados
mejor por la figura de la derecha.
Como PS = MS = SQ ⇒ MS = SQ = c/2 ∧ p = q
Como PS = MS = SQ ⇒ PS = c/2
Y notando que satisfacen el teorema de Euclides:
h 2 = pq
2
c c
⎛c⎞
⎜ ⎟ = •
⎝2⎠ 2 2
⇒ PS es también altura.
⇒ PSM = 90º. Alternativa B).
15. En el triángulo ABC, rectángulo en C, CD = 8 [cm] y AB = 20 [cm]. Si AD < BD ,
entonces AD =
A) 4[cm]
B) 6 [cm]
C) 8 [cm]
D) 9 [cm]
E) 16 [cm]
Solución:
Sea AD = x. Si AB = 20 [cm], entonces
AD + DB = 20
x + DB = 20
DB = 20 – x
Y del enunciado: hc = 8 [cm];
Reemplazando las dos expresiones anteriores en el teo. de Euclides referido a la altura:
h c = pq
82 = (20 − x ) x
64 = 20 x − x2
x2 − 20 x + 64 = 0
( x − 16)( x − 4) = 0 ⇒ x − 16 = 0 ∨ x − 4 = 0
⇒ x = 16 ∨ x = 4
⇒ ( AD = 16 ∧ DB = 4 ) ∨ ( AD = 4 ∧ DB = 16 )
(Teniendo presente que hemos llamado AD = x y que AD + DB = 20)
Como AD < BD ⇒ AD = 4 [cm] .
Alternativa A)
Parinacota, Quilicura.2009
7
Prof.: Guillermo Corbacho C.
16. En el triángulo ABC, rectángulo en A, AD = 6[cm] y DC = 4 [cm]. ¿Cuál es el área
del triángulo ABD?
A) 12 [cm 2 ]
B) 24 [cm 2 ]
C) 27 [cm 2 ]
D) 39 [cm 2 ]
E) 54 [cm 2 ]
Solución:
h•base
.
2
Ya tenemos el valor de la altura, que es el segmento perpendicular a la
ha = AD = 6 [cm].
base BC , trazada desde el vértice A.
Nos falta el valor de la base, que es la hipotenusa.
Sin embargo, ella se obtiene de la suma de las proyecciones BD y
DC , esta última vide 4 [cm].
Aplicando Teorema de Euclides, que relaciona a la altura con las
proyecciones, obtenemos:
El área general de todo triángulo viene dado por A =
h2 = BD•DC
36
=9
4
Conocidas las proyecciones, conoceremos la medida de la base BC , igual a:
BD + DC = 9 + 4 = 13
Luego, reemplazando este valor en la fórmula del área, esta nos queda:
6•13
A=
= 39 ⎡⎣ cm 2 ⎤⎦
2
Alternativa D)
36 = BD•4 ⇒ DB =
17. Si el triángulo ABC es rectángulo en C e isósceles, con AD = 4 [cm]. Entonces, su área
es igual a:
2
A) 8 [cm ]
2
B) 16 [cm ]
2
C) 32 [cm ]
2
D) 48 [cm ]
2
E) 64 [cm ]
Solución:
En todo triángulo isósceles, la altura bajada desde el ángulo del vértice coincide no solo
con su bisectriz, sino además, con el punto medio del lado opuesto –esto es, es también
transversal de gravedad del triángulo.
Esto implica que AD = DB = 4 [cm] y AB = 8 [cm].
h • base h • AB h • 8
(*)
El área del triángulo viene dado por A =
=
=
= 4h [cm2]
2
2
2
Para conocer la altura, usamos el valor de las proyecciones que esta determina, con el teo.
de Euclides relativo a la altura:
h 2 = AD • DB
= 4•4
= 16
⇒h=4
Finalmente, la expresión del área (*) nos queda:
4 • 4 = 16 [cm2]
Alternativa B).
Parinacota, Quilicura.2009
8
Prof.: Guillermo Corbacho C.
18. En la figura, BC = 10 y CD = 6, entonces AD mide:
A) 4
B) 4,5
C) 5
D) 6
E) 8
Solución:
Para el triángulo BCD, rectángulo en D, notamos que dos de los lados resultan de
amplificar por 2 el trío Pitagórico fundamental 3, 4, 5. El valor faltante es BD = 8.
Para hallar el valor de la proyección AD , notamos que tenemos el valor de la altura y el
de la otra proyección. Eso basta:
hc2 = AD•DB
62 = AD•8
36 = 8AD ⇒ AD =
36 9
= = 4,5
8 2
Alternativa B)
19. Se afirma que cada uno de los siguientes triángulos ABC son rectángulos.
De las afirmaciones, es (son) verdadera(s):
A) Solo I
B) I y II.
C) II y III
D) I y III
E) Todas
Solución:
Notamos que calculando mentalmente hc2 = pq en todos los triángulos. Estos satisfacen
el teorema de Euclides relativo a la altura, válida sólo en triángulos rectángulos. Por lo
tanto:
Alternativa E).
Parinacota, Quilicura.2009
9
Prof.: Guillermo Corbacho C.
c
20. En el ΔABC, rectángulo en C, hc = . En relación a esto se afirma que:
2
2
III. p = q
p
I. ( p + q ) = 4 pq
II. q =
2
De estas afirmaciones es(son) verdadera(s):
A) Solo I
A) Solo II
B) Solo III
C) I y II
D) I y III
Solución:
Analicemos I, II y III.
2
⎛
⎞
I. ⎜ p + q ⎟ = 4 pq
⎜
⎟
⎝ c ⎠
h 2
II. q =
III. Reemplazando p = q en
p
⇒ p = 2q
2
2
⎛
⎞
Reemplazando en ⎜ p + q ⎟ = 4 p q
c
⎟
I,
que
es ⎜⎝ q
q
⎠
c 2 = 4hc2 / extrayendo ra verdadero.
2
( 2q ) = 4q 2
2
2
= 2hc
c
⎛
⎞
Lo cuál es una aplicación de
⎜
p + q⎟ = 4 p q
c
propiedad de potencias.
⎜
⎟
= hc
2
q
2
q
⎝
⎠
2
III. Es verdadera.
2
2
( 3q ) = 8q
Lo cuál es verdadero, pues se
/:q 2
9 q 2 = 8q 2
indica en el enunciado.
9=8
Lo cuál es falso.
I y III son verdaderas.
Alternativa E)
21. De acuerdo a los datos de la figura, ¿cuál de las siguientes afirmaciones es verdadera?
A) h 2 = 2 p + 2q
B) h 2 = pq
C) h 2 = 4 pq
D) h 2 = 4 pq 2
E) h 2 = 4 p 2 q
Solución:
Todas las alternativas, así como las proyecciones sobre la hipotenusa proporcionadas en
la figura, sugieren la revisión del teorema de Euclides relativo a la altura.
Esta establece
h 2 = pq
Con p y q proyecciones sobre la hipotenusa.
Sin embargo, ella expresa la siguiente idea:
“El cuadrado de la altura bajada desde el ángulo recto es igual al producto de las
proyecciones de los catetos sobre la hipotenusa”.
La alternativa b) expresa algebraica y usualmente tal idea. Pero en este caso las medidas de
las proyecciones sobre la hipotenusa son 2q y 2p. Por lo que el teorema de Euclides
h 2 = 2q • 2 p = 4 pq
queda:
Alternativa B).
Parinacota, Quilicura.2009
10
Prof.: Guillermo Corbacho C.
22. El ΔABC está inscrito en la ⊗ de centro en O y radio R, tal que CD ⊥ AB y suponga
R
que CD = , entonces la medida de OD es:
2
R
A)
2
B) R 3
C) R 5
R
D)
3
2
2R
E)
3
Solución:
Hay que tener presente que el ΔABC es rectángulo en el vértice C, dado que su
hipotenusa coincide con el diámetro de la ⊗. Por lo tanto se cumplen los teoremas
pertinentes a relaciones métricas en un Δ rectángulo.
Aquí la altura está en función del radio. Y la hipotenusa AB = 2R. Sea x = AD.
Por Euclides referido a la altura, tenemos:
CD 2 = AD • DB
2
⎛R⎞
⎜ ⎟ = ( 2R − x ) x
⎝2⎠
R2
= 2 Rx − x 2
4
x 2 − 2 Rx +
R2
=0
4
/•4
4x 2 − 8Rx + R 2 = 0
Lo que nos conduce a una ecuación cuadrática para x con a = 4; b = −8R y c = R2.
−b ± b 2 − 4ac 8 R ±
x=
=
2a
( −8 R )
2
8
− 4 ( 4) ( R2 )
=
8r ± 64r 2 − 16r 2 8R ± 48 R 2
=
8
8
=
8 R ± R 16 • 3
8
8R ± 4 R 3
8
R 3
= R±
2
=
Ahora bien, de la figura se desprende que:
OD + x = R
⇒
OD = R − x
⎛
R 3⎞
R 3
= R − ⎜⎜ R ±
⎟⎟ = ∓
2 ⎠
2
⎝
Como no hay medidas negativas en la geometría euclidiana, se toma la solución positiva.
Alternativa D).
Parinacota, Quilicura.2009
11
Prof.: Guillermo Corbacho C.
II.2. Teorema de Euclides referido a los catetos
23. De acuerdo con los datos indicados en la figura, el área sombreada es:
A) pq
B) bc
C) a 2
D) b 2
E) hc2
Solución:
El área del rectángulo se obtiene con el producto de las medidas de dos lados contiguos.
En este caso,
A = cq
Pero, cq = b 2 (por teorema de Euclides referido al cateto b)
Alternativa D).
24. En el triángulo ABC rectángulo en C, BD = 15 [cm] y AB = 20 [cm]. Entonces, la
medida de BC es:
A) 10 3 [cm]
B) 10 [cm]
C) 35 [cm]
D) 400 [cm]
E) Ninguna de las anteriores.
Solución:
Por Euclides:
a 2 = cp
= 20•15
= 300
⇒ a = 300 = 100•3 = 10 3
Alternativa A).
25. En el triángulo, rectángulo en C, que se presenta
q = 12 [cm] y p = 4 [cm]. Mientras, la medida del lado a es:
A)
B)
C)
D)
E)
en
este
ejercicio,
8 3 [cm]
6 [cm]
8 [cm]
4 [cm]
Ninguna de las anteriores.
Solución:
Por teorema de Euclides relativos a los catetos:
a 2 = cp
= (q + p)p
= 16•4
= 64
⇒ a = 8 [cm]
Alternativa C).
Parinacota, Quilicura.2009
12
Prof.: Guillermo Corbacho C.
26. En un triángulo rectángulo, un cateto mide 8 [cm] y la proyección del otro cateto sobre
la hipotenusa mide 12 [cm], entonces, la medida de la proyección del primer cateto es:
A) 6 [cm]
B) 20 [cm]
C) 4 [cm]
D) 18 [cm]
E) 7,5 [cm]
Solución:
Es mejor ilustrar gráficamente la información, tal como muestra la figura de la derecha.
b 2 = cq
64 = ( q +12 ) q
64 = q 2 +12q
0 = q 2 +12q − 64
0 = (q +16)(q − 4) ⇒ q +16 = 0 ∨ q − 4 = 0
⇒ q = −16 ∨ q = 4
Como solo hay medidas geométricas positivas, q = 4 .
Alternativa C).
27. Si AB = 9 [cm] y con la información entregada en el triángulo rectángulo ABC,
¿Cuánto mide x?
A) 3
B) 4
C) 5
D) 6
E) 7
Solución:
Reemplazando los datos del enunciado y por teorema de Euclides relativo al cateto a, se
tiene:
a 2 = cp
Alternativa B)
62 = 9 x
36 = 9 x
⇒4=x
28. En el ΔABC, rectángulo en C, AD = 15 [cm] y AB = 20 [cm]. Entonces la medida de
AC es:
A) 10 3 [cm]
B) 10 [cm]
C) 35 [cm]
D) 400 [cm]
E) Ninguna de las anteriores.
Solución:
AB = 20 [cm] es la hipotenusa c, AC es el cateto b y AD es su
proyección q, donde por teorema de Euclides referido a los
catetos:
b 2 = cq
= 20•15
= 300
⇒ b = 300 [cm] = 100•3 [cm] = 10 3 [cm]
Parinacota, Quilicura.2009
Alternativa A)
13
Prof.: Guillermo Corbacho C.
29. En el ΔABC rectángulo en C, q = 4 [cm] y p = 12 [cm]. Entonces la medida del lado a
es:
A) 8 3 [cm]
B) 8 [cm]
C) 6 [cm]
D) 4 [cm]
E) Ninguna de las anteriores.
Solución:
Con los datos del enunciado se tiene c = 16 [cm].
Y el valor del cateto a lo hallamos gracias al teorema de Euclides relativo a los catetos:
a 2 = cp
= 16•12
⇒ a = 16•12
42
4•3
= 4 4 •3
22
= 4•2 3
= 8 3
Alternativa A).
30. En el Δ rectángulo de la figura, BC = 5 [cm] y DB = 4 [cm]. Entonces, AD = ?
25
A)
[cm]
4
5
B) [cm]
2
25
[cm]
C)
2
9
D) [cm]
4
E) No se puede determinar.
Solución:
Se tiene la medida del cateto a y de su proyección sobre
la hipotenusa. Así que usaremos Euclides -relativo a los
catetos-, para hallar c y la diferencia con DB = 4 nos
dará la medida AD.
a2 = c • p
52 = c • 4
25
= c
4
25
= ( AD + 4 )
4
25
− 4 = AD
4
25 − 4•4
= AD
4
9
[cm] = AD
4
Alternativa D)
Parinacota, Quilicura.2009
14
Prof.: Guillermo Corbacho C.
31. Respecto del ΔABC, rectángulo en C, se afirma que se cumple:
a2 p
a b
I. 2 =
II. a • b = c • hc
III. =
b
q
p q
A) Solo I
B) Solo II
C) Solo III
D) I y II
E) Todas
Solución:
Analicemos cada una de las alternativas:
I. El hecho de que aparezcan a 2 y b 2 con p y q sugiere ver el teorema de Euclides
relativo a los catetos.
a2 = c • p
(1)
2
b = c•q
(2)
Dividiendo lado a lado la expresión (1) por (2) obtenemos:
a2 c • p
=
•
b2 c • q
a2 p
⇒ 2 =
-conocido como el teorema de la razón de los cuadrados de los catetos.
b
q
Por lo tanto, I se cumple.
II. a • b = c • hc
Es difícil ver alguna relación que se cumpla. Esto se mantendrá así hasta no formar
alguna igualdad de razones o alguna proporción que podamos verificar geométricamente.
Por esto vamos a “traspasar” de cada lado de la supuesta igualdad, a un factor del
producto como divisor del otro lado de la igualdad. Obtenemos así:
a c
a hc
y
=
=
hc b
c b
La primera igualdad señala que en el ΔABC, el mayor de los catetos es a la hipotenusa
como en el ΔADC la misma relación: el mayor de los catetos es a su hipotenusa.
Lo cuál es verdadero, pues hay una comparación de lados homólogos. Por lo tanto, nos
basta para indicar que II es verdadera.
En todo caso, también nos basta lo que hubiese resultado de la segunda igualdad. Ella
señala que: en el ΔDBC, la hipotenusa es al menor de los catetos, como en el ΔABC la
misma relación: la hipotenusa es al menor de los catetos. Otra comparación de lados
homólogos, por lo que también habríamos podido concluir que II es verdadera.
a b
=
p q
Esta supuesta igualdad nos indica que: en el ΔDBC, la hipotenusa es al mayor de los
catetos como en en el ΔACD la hipotenusa es al menor de los catetos. Lo cual no es una
comparación de lados homólogos o similares. III es falsa.
Solo I y II son verdaderas.
Alternativa D).
III.
Parinacota, Quilicura.2009
15
Prof.: Guillermo Corbacho C.
II.3. Ejercicios combinados referidos a la altura como a los catetos
32. En el triángulo ABC, rectángulo en C, ¿Cuál de las siguientes aseveraciones es (son)
SIEMPRE verdadera(s)?
I. CD • AB = AC • BC
II. AC = AD • AB
AD • BD
III. CD =
CD
A) Solo I
D) I y III
B) Solo II
E) I, II y III
C) I y II
Solución:
Analicemos I, II y III.
a •b
c
CB • AC
Es decir : CD =
AB
⇒ CD • AB = AC • CB
I. Se sabe que : hc =
/ • AB
Recordemos para el lado derecho, que el oden de los factores no
altera el producto.
Por lo tanto, I) es verdadera.
b2 = q • c
II. Por teo. de los catetos, para el lado AC = b , tenemos:
Mientras que la igualdad dada AC = AD•AB nos dice solo que: b = q • c
Lo cual es falso, al no estar b elevado al cuadrado.
2
III. El teo. de la altura nos indica que : hc 2 = p • q ⇒ ( CD ) = DB • AD
⇒ CD =
AD • DB
CD
Por lo tanto, III. se cumple.
Solo I y III son aseveraciones verdaderas.
Alternativa D).
Parinacota, Quilicura.2009
16
Prof.: Guillermo Corbacho C.
33. ¿En cuál (es) de las siguientes figuras se cumple que c 2 = ab ?
I.
II
A)
B)
C)
D)
E)
Solo I
Solo II
Solo III
I y II
Todas.
III
DE // AB
Solución:
Hay que analizar cada figura:
Hay que notar que el la denominación de los lados y segmentos, no son las usuales en los
triángulos rectángulos. Pero las denominaciones de los lados y segmentos es lo de menos,
lo que importa es si se cumple que c 2 = ab los teoremas geométricos en I, II y III.
I.
En el teo. de Euclides relativo a la altura. El cuadrado de ella es igual al producto
de las proyecciones de los catetos.
Si c es la altura; a y b las proyecciones de los catetos, entonces debe cumplirse en la
fig. que:
II.
I es verdadera.
c 2 = ab
En la fig. c es cateto, a es hipotenusa y b proyección del cateto a.
Por el teo. de los catetos: el cuadrado de cada uno de ellos por separado es igual, al
producto de la hipotenusa por su respectiva proyección. En la fig. de II, es:
c 2 = ab
III.
II es verdadera.
c b y haciendo producto cruzado
Por Thales: = ⎯⎯
⎯⎯⎯⎯⎯⎯⎯⎯⎯→ c 2 = ab
a c
Luego, en I, II y III se cumple que: c 2 = ab
Alternativa E)
Parinacota, Quilicura.2009
17
Prof.: Guillermo Corbacho C.
III. Teorema Particular de Pitágoras
III.1. Tríos Pitagóricos
34. Un grupo de amigos debe cruzar un río. Para hacerlo, ubican el bote justo frente al lugar
donde desean llegar, pero la corriente los lleva río abajo, a 120 [cm] del lugar deseado.
Si el ancho del río es de 90 [m]. ¿Cuánto recorrió el bote?
A) 135 [m]
B) 125 [m]
C) 150 [m]
D) 210 [m]
E) Ninguna de las anteriores.
Solución:
Si ilustramos la situación y pensamos en el trío
pitagórico fundamental 3, 4 y 5. Notamos que al
amplificar a este por el número natural 30, obtenemos
el trío Pitagórico: 90, 120 y 150.
Al comparar tales valores con los datos ilustrados en la
figura, notamos que el valor faltante es 150 [m], que
viene a ser la medida del recorrido buscado.
Alternativa C).
35. ¿Cuánto mide CD en el triángulo ABC si AC = 30 [mm] y BC = 40 [mm]?
A) 50 [mm]
B) 40 [mm]
C) 30 [mm]
D) 25 [mm]
E) 24 [mm]
Solución:
Como CD es altura trazada desde un ángulo de 90º, su medida viene dada por:
producto de los catetos ab 30 • 40
hc =
=
=
c
c
hipotenusa
Todo se reduce a conocer el valor de la hipotenusa c = AB. Pero ello es fácil conociendo
el valor de los dos catetos. Pues resultaría de la aplicación del teo. Particular de Pitágoras.
Pero es aún más fácil, solo basta notar que los catetos resultan de amplificar por 10 los
valores 3 y 4 del trío fundamental 3, 4 y 5. Por lo que la hipotenusa ha de obtenerse de
amplificar por 10 al valor del otro trío fundamental, es decir, de 5.
c = 5 • 10 = 50 [mm]
Así,
30•40 30•40 120
hc =
=
=
= 24 [mm] Alternativa E)
50
50
5
36. El radio de la circunferencia de centro O mide 4 [cm] y AC mide 10 [cm]. ¿Cuánto
mide la cuerda BC tangente a la circunferencia?
A) 2,4
B) 3,6
C) 4,8
D) 5,0
E) 6,0
Solución:
En el triángulo ABC rectángulo en B, tenemos la medida de dos de sus tres lados:
AC = 10 [cm] y AB = 8 [cm]
Y podemos notar que estos resultan de amplificar por dos a los números 4 y 5 del trío
Pitagórico fundamental: 3, 4 y 5.
Por lo tanto, nos falta amplificar por dos al número 3 de tal trío para hallar BC.
BC = 2 • 3 = 6 [cm].
Alternativa E)
Parinacota, Quilicura.2009
18
Prof.: Guillermo Corbacho C.
37. Una escalera de bomberos de 13 [m] de longitud está apoyada contra
una pared. Si el pie de la escalera dista 5 [m] de la base de la pared.
¿Qué altura alcanza en ella?
A) 13 [m]
B) 12 [m]
C) 18 [m]
D) 15 [m]
E) 10 [m]
Solución:
5, 12 y 13 son un trío pitagórico fundamental.
En la fig. el número faltante del trío es 12.
Por lo tanto, la altura alcanzada en la escalera es de 12 [m].
Alternativa B).
Método alternativo:
Si resultase difícil memorizar este trío pitagórico fundamental, siempre la solución se
puede obtener el teo. particular de Pitágoras, cuya colección de ejercicios se presenta a
continuación:
h2 + 52 = 132
h2 + 25 = 169
h2 = 169 − 25
= 144
h = 12 [m]
Alternativa B).
38. Si los catetos de un triángulo rectángulo miden 5 [cm] y 12 [cm] respectivamente,
entonces, la altura trazada hacia la base, siendo esta la hipotenusa, mide:
17
A)
[cm]
13
7
B) [cm]
5
60
[cm]
C)
13
D) 30 [cm]
E) Ninguna de las anteriores.
Solución:
ab
, válida sólo para triángulos rectángulos.
c
Con a y b catetos; c hipotenusa, tenemos: c = 13, pues 5, 12 y 13 forman un trío
pitagórico. Reemplazando estos valores en la expresión para la altura.
5•12 60
=
hc =
13
13
Alternativa C).
Usando hc =
Parinacota, Quilicura.2009
19
Prof.: Guillermo Corbacho C.
III.2. Teorema Particular de Pitágoras
39. Basándose en los datos de la figura, la altura CD mide:
A) 6 3 [ m]
B)
C)
D)
E)
4 3 [m]
24 [m]
12 [m]
Ninguna de las anteriores.
Solución:
CD es la altura bajada desde el ángulo de 90º. Por lo que podemos hallarla con:
ab
Donde a = 8 [m] y b son los catetos, así como c = 16[ m] la hipotenusa.
h=
c
Para hallar la medida del cateto b, aplicamos Pitágoras:
a 2 + b 2 = c 2 ⇒ 82 + b 2 = 16 2
64 + b 2 = 256
⇒ b 2 = 256 − 64 = 192
Así, CD = h =
⎯⎯⎯
→ b = 192 = 64•3 = 8 3
ab 8•8 3
=
=4 3
16
c
Alternativa B)
40. En el ΔABC, p 2 + q 2 + 2 pq =
A) 196
B) 100
C) 196 + 2pq
D) 100+ 2pq
E) Ninguna de las anteriores.
Solución:
Recordemos que:
p 2 + q 2 + 2 pq = ( p + q )
2
Expresamos el trinomio perfecto en su binomio al cuadrado.
= c2
De la figura, la suma de p y q es la hipotenusa.
= 62 + 82
Por Pitágoras.
= 102
O también, igual a 36 + 64
= 100
6, 8 y 10 son un trío Pitagórico.
Alternativa B)
41. En el triángulo de la figura, a 2 + b 2 + 2ab =
A) 169
B) 196
C) 169 + 2ab
D) 196 + 2ab
E) 287
2
Solución: Recordemos que a 2 + b2 + 2ab = ( a + b )
Y de la figura, a + b = c
= c2
= 52 +122
Por Pitágoras.
= 132
(5, 12 y 13 son un trío Pitagórico)
O también, 52 +122 = 25 +144
= 169
Parinacota, Quilicura.2009
Alternativa A)
20
Prof.: Guillermo Corbacho C.
42. En una circunferencia se trazan dos cuerdas, AC = 5 [cm] y BC = 12 [cm], de modo
que AB es diámetro. La longitud del BCA es:
A) No se puede determinar.
B) 40 cm.
C) 13 π cm.
D) 6,5 π cm.
E) Ninguna de las anteriores.
Solución:
Recordemos que todo ángulo inscrito que subtiende el diámetro de
una circunferencia es recto. Por lo tanto, el triángulo ABC es
rectángulo en C.
Además, la medida de BCA es igual al semiperímetro de la
circunferencia. Y conocemos expresiones para el calcularlo.
Perímetro = 2π R = π D , donde D es el diámetro AB o hipotenusa
del triángulo rectángulo en C. Para hallarlo podemos aplicar
Pitágoras. Aunque es mejor, recordar el trío Pitagórico fundamental
5, 12, 13. Y en la figura, 13 es el valor faltante, por lo que AB = D = 13 π . Así,
Perímetro = 2π R = π D = 13 π ⇒ BCA = semi perímetro es (13π)/2 = 6,5π.
Alternativa D).
43. Un rectángulo de 12 [cm] de ancho y con un perímetro de 68 [cm] tiene una diagonal
de:
A) 157 [cm]
68
[cm]
B)
12
C) 628 [cm]
D) 314 [cm]
E) 2 157 [cm]
,Solución:
Es siempre conveniente dibujar la figura que se describe
con los datos que de ella tenemos. Ella puede verse a
continuación:
La representación nos ilustra la distribución de 24 [cm].
Los cm que faltan para completar los 68 [cm] de perímetro
son: 68 – 24 = 44 [cm], los cuáles se distribuyen en partes
iguales en los dos lados paralelos restantes, AB y DC .
44
Obteniéndose así:
[cm] = 22 [cm] de medida en tales
2
lados. Tal como se ilustra en la segunda figura de la derecha.
Ahora es fácil de observar que la diagonal es la hipotenusa de dos triángulos rectángulos,
que como son congruentes, basta con trabajar en uno de ellos.
Así, sobre el ∆ABC rectángulo en B, aplicamos Pitágoras:
d 2 = 222 + 122 = 484 + 144 = 628
d = 628 = 4 • 157 = 2 157
Alternativa E)
Parinacota, Quilicura.2009
21
Prof.: Guillermo Corbacho C.
44. Si en un ∆ rectángulo la hipotenusa mide x 2 + y 2 , mientras que uno de sus catetos mide
2 xy . ¿Cuál es la medida del otro cateto?
A) x + y
B) x 2 − y 2
C)
( x + y)
2
D) x − y
E) 4 x 2 y 2
Solución:
Por Pitágoras:
c2 = a 2 + b2
Y reemplazando los datos del enunciado en la igualdad anterior:
(
x2 + y 2
)
2
2
= ( 2xy ) + b 2
x4 + 2 x2 y 2 + y 4 = 4 x2 y 2 + b2
x4 − 2 x2 y 2 + y 4 = b2
( x2 − y 2 )
2
= b2
x2 − y 2 = b
La alternativa correcta es B).
45. Si el área de un triángulo equilátero es 25 3 [m 2 ] , entonces el lado mide:
A)
B)
C)
D)
5 3 [m]
10 [m]
100 [m]
20 3 [m]
E) 50 3 [m]
Solución:
El área de todo triángulo viene dado por:
a
ah
base • altura 2
= •h =
(*)
A=
2
2
4
Sea el triángulo ABC equilátero de lado a.
a 3
.
La altura viene dada por
2
Y puede obtenerse usando Pitágoras sobre cualquiera de los triángulos que tienen por
uno de sus lados a la altura h.
El área del triángulo, tras reemplazar el valor de la altura en (*), nos queda:
a 3
a•
2
2 =a 3
A=
2
4
Al igualar tal valor del área con 25 3 [m 2 ] , obtenemos:
a2 3
⇒ 100[m 2 ] = a 2
4
⇒ 10 [m] = a
Alternativa B).
25 3 [m 2 ] =
Parinacota, Quilicura.2009
22
Prof.: Guillermo Corbacho C.
46. Si uno de los catetos de un triángulo rectángulo mide el doble del otro. ¿Cuánto mide el
menor de ellos si la hipotenusa mide 5 2 [cm] ?
A) 10 [cm]
B) 5 2 [cm]
C) 2 5 [cm]
D) 10 [cm]
E) Ninguna de las anteriores.
Solución:
Sean a, b los catetos con a = 2b y c la hipotenusa.
Por Pitágoras:
a 2 + b2 = c 2
Reemplazando los datos :
(2b) 2 + b 2 = (5 2 )2
5b 2 = 25•2
Simplificando por 5
→ b = 10
b 2 = 5•2 = 10 ⎯⎯⎯
Alternativa D).
47. Si uno de los catetos de un triángulo rectángulo mide el doble del otro. ¿Cuánto mide su
área si la hipotenusa mide 10 [m] ?
2
A) 20 [m ]
B) 10 3 [m 2 ]
C) 4 5 [m 2 ]
2
D) 5 5 [m ]
2
E) 5 3 [m ]
Solución:
En un triángulo rectángulo, el área puede obtenerse con A =
Y con a = 2b y c la hipotenusa.
Por Pitágoras:
a 2 + b2 = c 2
Reemplazando los datos :
ab
, con a, b los catetos.
2
(2b)2 + b 2 = (10) 2
5b 2 = 100
Simplificando por 5
b 2 = 20 ⎯⎯⎯
→ b = 20 = 4•5 = 2 5
⇒a=4 5
(por ser a = 2b)
Con los valores de a y b conocidos, reemplazamos en la fórmula del área
ab 4 5•2 5
A=
=
= 4•5 = 20 [m2]
2
2
Alternativa A).
Parinacota, Quilicura.2009
23
Prof.: Guillermo Corbacho C.
48. Si las medidas de los catetos de un triángulo rectángulo están en la razón 1 : 2 y su
2
área es de 25 [cm ]. Entonces, la hipotenusa mide:
A) 5 3 [cm]
B) 5 5 [cm]
C) 10 [cm]
D) 10 3 [cm]
E) 10 5 [cm]
Solución:
Sean a y b los catetos. Como estos están en la razón de 1:2
a 1 Producto cruzado
(*).
⇒
= ⎯⎯ ⎯⎯⎯⎯⎯⎯→ 2a = b
b 2
ab
Y del área de un triángulo rectángulo:
25 [cm 2 ] =
2
El área se puede obtener en función del semiproducto de los catetos.
a • 2a
⎯⎯⎯
→ 5 [cm] = a
25 [cm] =
= a2
2
(*)
⎯⎯⎯
→ b = 2a = 10 [cm]
Con los catetos
a
y
b
conocidos, se puede obtener la hipotenusa por
Pitágoras : c 2 = a 2 + b 2
c 2 = 25 +100
= 125 [cm2 ] ⇒ c = 125 [cm] = 25•5 [cm] = 5 5 [cm]
Alternativa B).
49. La cuerda que une el extremo superior de un velero con su proa es 8,5 [m]. Si el mástil
tiene una altura de 6 [m], ¿Qué distancia aproximada hay del mástil a la proa?
A) 6,02 [m]
B) 10,4 [m]
C) 14,5 [m]
D) 7 [m]
E) Ninguna de las anteriores.
Solución:
Si se ilustra la información, podemos visualizar
fácilmente la formación de un triángulo rectángulo y
su posterior aplicación del teorema de Pitágoras.
(8,5)
2
= 62 + x 2
72, 25 = 36 + x 2
36, 25 = x 2 ⇒ x ≈ 6 ∨ x ≈ 6, 02
Alternativa A)
Parinacota, Quilicura.2009
24
Prof.: Guillermo Corbacho C.
50. Si uno de los catetos tiene 5 unidades menos que la hipotenusa y el otro cateto mide
5 3 [cm] . ¿Cuánto mide el perímetro del triángulo?
A) 20 3 [cm]
B) 5 [cm]
C) (10 + 10 3) [cm]
D) (15 + 5 3) [cm]
E) Ninguna de las anteriores.
Solución:
Sean a, b los catetos y c la hipotenusa respectivamente.
Como datos: a = (c − 5) [cm], b = 5 3 [cm] .
(*)
Si sólo tuviésemos el valor de c, también obtendríamos el del cateto a y ahí podríamos
sumar los lados para obtener el Perímetro.
Una cosa que sabemos es que los lados a, b y c satisfacen el teorema de Pitágoras, esto es:
a 2 + b2 = c2
(c − 5) 2 + (5 3) 2 = c 2
al reemplazar los datos de (*)
Ahora tenemos solo una incógnita y una ecuación. Podemos resolver para c.
c 2 −10c + 25 + 25•3 = c 2
100 = 10c
10 [cm] = c
Reemplazando este valor de c en (*) , obtenemos a = 5 [cm].
Finalmente, conocemos la medida de todos los lados del Δ. Su perímetro es:
a + b + c = 5 + 5 3 + 10
= 15 + 5 3
Alternativa D).
51. Se tiene un triángulo rectángulo isósceles de hipotenusa 2ab 2 . Si se construye un
cuadrado sobre uno de sus catetos, el perímetro de este cuadrado es:
A) ab 2
B)
C)
D)
E)
4ab2 2
2 a 2b 2
2ab 2
4ab
Solución:
La situación puede ilustrarse como a continuación:
Por Pitágoras, podemos obtener el valor de un lado:
c 2 = a 2 + b2 ⎫
⎪⎪
= x 2 + x 2 ⎬ ⎯⎯→ c = x 2
⎪
= 2 x2
⎪⎭
2ab 2 = x 2
2ab 2
=x
2
2ab 2 = x
El perímetro del cuadrado es cuatro veces el valor de x.
P = 4 2 ab 2
= 4ab 2 2
Alternativa B)
Parinacota, Quilicura.2009
25
Prof.: Guillermo Corbacho C.
52. Si las medidas de los catetos de un triángulo rectángulo están en la razón 1 : 2 y su área
2
es 25 cm , entonces la hipotenusa mide:
A) 5 3 [cm]
B) 5 5 [cm]
C) 10 [cm]
D) 10 3 [cm]
E) 10 5 [cm]
Solución:
El área de un triángulo rectángulo puede obtenerse como el semiproducto de los catetos.
Esto es,
ab
A=
2
Que los catetos estén en la razón 1 : 2 significa que un cateto está formado por cierta
parte p y el otro por 2p. Tienen medida p y 2p. Todo se reduce a hallar el valor de p.
Así, la expresión anterior nos queda:
p•2p
A=
2
2
25 = p
/
5= p
⇒ Los catetos miden p = 5 y 2p = 2 • 5 = 10.
Los cuáles no forman parte de un trío pitagórico. Por lo tanto, para hallar la hipotenusa,
aplicamos solo el teo. particular de Pitágoras:
c2 = a 2 + b2
= 52 + 102
= 125
⇒ c = 125 = 25 • 5 = 5 5 [cm]
Alternativa B)
53. Para un hexaedro regular de la figura de lado 5, ¿cuánto mide el área achurada ABCD?
A) 25
B) 25 2
C) 50
D) 50 2
E) 5 2
Solución:
El hexaedro regular es un cubo.
El área del rectángulo ABCD viene dado por el producto de dos lados consecutivos,
Área = AD • AB
donde el lado AD = 5.
(*)
= 5 AB
Para hallar el valor del lado AB, usamos Pitágoras en el ∆ superior.
2
2
2
(AB) = 5 + 5
2
(AB) = 50 ⇒ AB =
50
Reemplazando el valor del lado AB en la expresión (*), pendiente del área
Área = 5 AB
No está tal expresión, pero se puede trabajar.
=
5 50
= 5 • 25 • 2 = 5 •5
Alternativa B)
Parinacota, Quilicura.2009
2 = 25 2
26
Prof.: Guillermo Corbacho C.
54. En la figura, MQ mide:
A) 5 [cm]
B) 5 [ cm ]
C) 3 3 [ cm]
D) 5 5 [ cm ]
E) 5 3 [ cm]
Solución:
Los números 10 y 15 no forman parte de un trío pitagórico fundamental. No son
múltiplos de 3, 4, 5 o de 5, 12 y 13 o de 8, 15 y 17. Por citar los más conocidos, por lo
tanto, aplicamos teo. particular de Pitágoras sobre el ΔPQM, rectángulo en Q, con 15
[cm] de hipotenusa:
(15)2 = (10 )2 + ( MQ )
( )
225 = 100 + MQ
(
⇒ MQ
MQ
)
2
2
2
Ahora despejaremosMQ
= 125
Extraeremos raíz cuadrada
= 125
Y disminuiremos la cantidad subradical
= 25•5 = 5 5
Alternativa D)
55. Si en un triangulo rectángulo, la suma de la medidas de los catetos a y b es 17 cm. y su
perímetro es 30 cm. ¿Cuál es la medida de la altura hc?
60
1
D)
A)
13
6
12
2
B)
E)
15
25
12
C)
13
Solución:
Señalamos la expresión para hallar la altura en función de los catetos:
ab
Necesitamos hallar los valores a, b y c
(i)
hc =
c
Los datos que nos dan son:
a + b = 17
(ii)
y a + b + c = 30 ⇒ c = 30 – 17 = 13
Ahora nos quedan dos incógnitas, los catetos a y b. Y para hallarlos, aún nos queda como
recurso aplicar el teo. de Pitágoras y la igualdad a + b = 17 que los relaciona:
a 2 + b 2 = 132
reemplazando en el binomio al cuadrado
( a + b )2 = 172 ⇒ a 2 + b2 + 2ab = 289
169
60
⇒ 2ab = 289 − 169 = 120 ⇒ ab = 60 ⎯⎯⎯⎯⎯⎯⎯⎯⎯→ hc =
Reemplazando en (i)
13
Alternativa A)
Parinacota, Quilicura.2009
27
Profesor: Guillermo Corbacho C.
56. En un triángulo ABC, rectángulo en A, el cateto AC = 2 y las transversales de
gravedad BM y AE son ortogonales. Calcular el valor de BC .
A) 1
B) 3/2
C) 2
D) 3
E) 3 2
Solución:
El dato que tenemos es que K es baricentro –intersección de las trasversales de gravedad,
esto implica que:
MK 1
AC
2
=
y
(*)
AM = MC =
=
KB 2
2
2
Tenemos expresiones de las medidas de los lados del ΔABM, por lo que aplicaremos los
teo. de relaciones métricas en el Δ solo a el. Conocemos la medida de uno de sus catetos
y nos piden la medida del otro. Además, tenemos la razón de sus respectivas proyecciones
sobre la hipotenusa BM .
Por el teo. de la razón de los catetos:
a2
p
=
2
q
b
Pero sobre el ΔAMB, rectángulo en A, esto es, con a =AM=
p MK 1
2
=
= :
; b=BC y
q KB 2
2
2
⎛ 2⎞
⎜
⎟
⎝ 2 ⎠ =1
( AB )2 2
2
⎛ 2⎞
2 1
Es importante notar que ⎜⎜
⎟⎟ = =
4 2
⎝ 2 ⎠
y
usar (*)
1
1
⇒ 2 =
2 2
( AB )
Haciendo producto cruzado:
2
2
= ( AB )
2
2
1 = ( AB ) ⇒ AB = 1
Ahora tenemos la medida de dos lados del ∆ABC, rectángulo en C. Podemos usar
nuevamente Pitágoras, para hallar la medida pedida:
2
2
⇒ (BC) = (AC) + (AB)
2
= ( 2)2 + (AB)
= 2 + 1
= 3
⇒ BC = 3
La respuesta es D).
Parinacota, Quilicura.2009
2
28
Profesor: Guillermo Corbacho C.
IV. Ejercicios combinados de Euclides con Pitágoras
57. El radio de la figura mide:
16
A)
3
34
B)
3
C) 19
25
D)
3
E) No se puede determinar.
Solución:
Hay que tener presente que todo triángulo inscrito, que subtiende
media circunferencia es recto. Así, el ∆ABC es rectángulo en C.
Además, el ∆DBC es rectángulo en D. En el se tienen los valores
8 y 10, que forman con 6 un trío Pitagórico resultante de
amplificar por dos el trío pitagórico fundamental 3, 4, 5:
3
6
4
8
5
10
/• 2
Por lo tanto, DB = 6.
Ahora hallaremos la medida del diámetro de la ⊗ para luego dividir tal valor por dos,
hallando así, el radio pedido.
Aplicando teo. de Euclides relativo a los catetos para el ∆ABC.
cp = a 2
c6 = 100
100 50
=
⇒ Radio = mitad del diámetro
6
3
25
=
3
Alternativa D).
⇒c=
También sirve para calcular la medida de la hipotenusa: hallar primero AD, sumarlo con
DB=6 y dividir tal suma por dos, para hallar el valor del radio.
Así, aplicando Euclides referido a la altura:
CD2 = AD•DB
64 = AD•6 ⇒ AD =
64 32
=
6
3
32
32 + 6•3 50
+6 =
=
3
3
3
25
=
Radio = mitad del diámetro
3
El diámetro de la ⊗ = AD + DB =
⇒
Como ya sabemos, alternativa D).
Parinacota, Quilicura.2009
29
Profesor: Guillermo Corbacho C.
58. El triángulo ABC es isósceles y rectángulo en C. Si BC = 2 2 , entonces AD + DC =
A) 4
B) 2 2
C) 4 2
D) 8
E) Ninguna de las anteriores.
Solución:
En todo triángulo isósceles, la altura bajada desde el ángulo del vértice coincide no solo
con su bisectriz, sino también, con el punto medio del lado opuesto. Esto implica que
AB
AD = AC =
, es decir, son la mitad de la hipotenusa.
2
Además, los lados opuestos a los ángulos basales tienen igual medida, por lo tanto,
AC = CB = 2 2.
Conocidos los dos catetos, podemos hallar el valor de la hipotenusa AB y luego, la
medida de sus mitades, mitades AD y AC en función de ella. Estas dos últimas medidas
nos determinarán DC por el teo. de Euclides.
Por Pitágoras:
AB 2 = AC 2 + BC 2
= (2 2) 2 + (2 2 ) 2
= 22 • 2 + 22 • 2
= 8+8
= 16
⇒ AB = 4 ⇒ AD = DB = 2
Para hallar el valor del trazo CD = hc , aplicamos ahora teorema de Euclides relativo a los
catetos:
hc2 = AD•DC = 4 ⇒ h = 2 = AD
Finalmente, AD + DC = 2 + 2 = 4
Alternativa A)
59. ¿Cuánto mide AD en el siguiente triángulo?
A) 16
B) 12
C) 10
D) 8
E) 6
Solución:
AD es proyección. Por lo tanto, para hallar su valor, conocida la otra proyección, basta
conocer la altura y aplicar el teorema de Euclides relativo a la altura. Ahora bien, para
hallar la altura, debemos aplicar el teorema de Pitágoras primero, en el triángulo ADC
rectángulo en D.
( AC ) 2 = (CD) 2 + ( DB ) 2 ⇒ 42 = (CD) 2 + 22
16 = (CD)2 + 4
12 = (CD) 2 ⇒ CD = 12
Y aplicando Euclides relativo a la altura:
( CD )
2
= AD • DB
⇒ 12 = AD • 2 ⇒ AD =
Alternativa E)
Parinacota, Quilicura.2009
12
=6
2
30
Profesor: Guillermo Corbacho C.
60. En el triángulo ABC, rectángulo en C, x mide:
A) 8
B) 12
C) 16
D) 32
E) 64
Solución:
x es la hipotenusa del triángulo ADC, rectángulo en D. Por lo tanto, nos bastaría conocer
el valor de los dos catetos de dicho triángulo y aplicar Pitágoras. Pero, solo conocemos la
medida de uno de los catetos.
Para obtener la medida de CD , reconocemos que dicho segmento es a su vez, altura del
ΔABC rectángulo en C. Y podemos aplicar en el, el teorema de Euclides relativo a la
altura, dado que conocemos las proyecciones que esta altura determina sobre la
hipotenusa AB.
Así,
CD2 = 4•12 ⎞
⎟ ⇒ CD = 48
= 48 ⎟⎠
Ahora, en el triángulo ADC, rectángulo en D, aplicamos Pitágoras para obtener el valor
de su hipotenusa x.
x 2 = CD2 + 42 ⎞
⎟
= 48 +16 ⎟ ⇒ x = 64 = 8
⎟⎟
= 64
⎠
Alternativa A).
61. ¿Cuál(es) de la(s) siguiente(s) relación(es) es(son) verdadera(s) con respecto al
triángulo ABC rectángulo en C?
I. CD 2 = 23, 04
II. BD = 2 AD
III. AB 2 = 100
A)
B)
C)
D)
E)
Solo I
Solo II
Solo III
I y III
II y III
Solución:
Lo primero es notar que los catetos 6 y 8 resultan de amplificar por 2 los valores del trío
Pitagórico fundamental 3, 4 y 5.
Por lo que la hipotenusa se obtendrá de amplificar también el otro valor del trío, esto es,
de 5 resultando ser igual a 10.
Como consecuencia de ello, BD = 10 – 3,6 = 6,4.
I. Ahora podemos confirmar o refutar la aseveración I.
Por Euclides:
2
CD = AD • BD
= 3,6 • 6,4
= 23,04
Así, I es verdadera.
II. Además, BD = 6,4 ≠ 2AD = 2 • 3,6 = 7,2
Por lo tanto, II es falsa.
III. Como la hipotenusa AB = 10 ⇒ AB 2 = 100 . Por lo tanto, III) es Verdadero.
Así, I y III son verdaderas. Alternativa D).
Parinacota, Quilicura.2009
31
Profesor: Guillermo Corbacho C.
62. El ΔABC es rectángulo en C. Entonces la medida de x es:
3
A)
2
B) 1
C) 5
D) 6,4
E) Ninguna de las anteriores.
Solución:
Lo primero es notar que los catetos 6 y 8 resultan de amplificar por 2 los valores 3 y 4 del
trío Pitagórico fundamental 3, 4 y 5. Por lo que, la hipotenusa se obtendrá de amplificar
el otro valor del trío, esto a 5 y por 2, lo que resulta ser igual a 10.
Por Euclides:
b2 = c• x
64 = 10 x
/
1
10
64
=x
10
6, 4 = x
Alternativa D)
63. En el ΔABC, rectángulo en C, se tiene DE // BC. ¿Cuál o cuáles de las siguientes
afirmaciones son verdaderas?
II. t • s = x 2
III. a 2 + p 2 = h 2
I. x • a = h 2
A) Solo I
B) Solo II
C) Solo III
D) I y II
E) Todas.
Solución:
Analicemos cada alternativa:
El hecho de que DE // BC nos hace ver que estamos frente a triángulos semejantes entre
sí.
I.
x • a = h2 ⇒ x • a = h • h
“Pasando alguno de los factores de cada producto, como divisor al otro lado de la
x h
igualdad, se puede reescribir como: =
h a
Lo que es una comparación de lados homólogos en los Δs EDC y DBC, entre las razones:
Dicha comparación es entre el menor de los catetos respecto a la hipotenusa, en cada Δ
señalado. Por lo tanto, I). Es una relación verdadera.
II. t • s = x 2 Es la expresión del teorema de Euclides relativo a la altura, en este caso,
sobre la hipotenusa del triángulo ADC rectángulo en D. II) es verdadera.
III. a 2 + p 2 = h 2
Sobre el ΔDBC, rectángulo en D, a es la hipotenusa. Su cuadrado no debe estar
acompañado de ningún sumando en la formulación del teo. de Pitágoras. La expresión
indica que la hipotenusa es h. Por lo tanto, III) es falsa.
Así, sólo I y II son ciertas.
Alternativa D).
Parinacota, Quilicura.2009
32
Profesor: Guillermo Corbacho C.
64. Según los datos de la figura, se puede afirmar que:
I. q = 1,8 [cm]
II. p = 3,2 [cm]
III. h = 5,76 [cm]
a) I y II
b) I y III
c) II y III
d) I, II y III
e) Ninguna de las anteriores.
Solución:
Claramente q + p = 5. Pues 3, 4 y 5 es un trío fundamental pitagórico.
Ahora bien, aplicando teorema de Euclides relativos a los catetos:
II. a 2 = cp
I. b 2 = cq
9 = 5p ⇒ p = 1,8
I) es correcta.
16 = 5 p ⇒ p = 3,2
II) es verdadera.
III. Aunque para hallar la altura h podemos emplear el teorema de Euclides relativo a la
altura, como hay decimales en el producto de p y q, es preferible usar
ab 3•4 12
=
= = 2, 4
h=
5
5
c
Luego, III) es falsa.
Luego, la alternativa correcta es A).
65. El ΔABC es rectángulo en C y AB = 2CD, se puede afirmar entonces que:
1
A) AD = DB
2
B) BC = 2AC
C) AB = 2AC
D) AD = DB
E) Ninguna de las anteriores.
Solución:
Aplicando Euclides referido a los catetos:
a 2 = cp
b 2 = cq
Al reemplazar el dato del enunciado: c = 2h nos queda:
a 2 = 2hp
(I)
b 2 = 2hq
(II)
Por Pitágoras, en Δs DBC y ADC respectivamente:
a 2 = p 2 + h2
(III)
b2 = q 2 + h2
(IV)
Al reemplazar (III) en (I) y (IV) en (II), obtenemos:
p 2 + h 2 = 2hp
q 2 + h 2 = 2hq
p 2 − 2hp + h 2 = 0
q 2 − 2hq + h 2 = 0
( p − h) 2 = 0
( q − h) 2 = 0
p=h
q=h
si p y q resultan iguales a una misma cantidad, entonces
ambos, p y q, son iguales entre sí (propiedad transitiva).
p=q
AD = DB
O bien,
Alternativa D)
Parinacota, Quilicura.2009
33