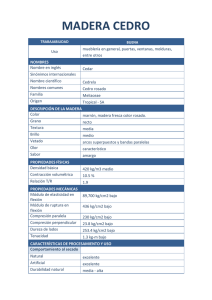
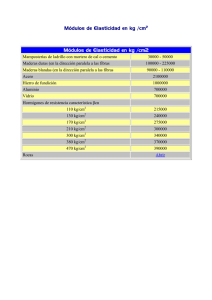
∑ = 0 ∑ = 0
Anuncio
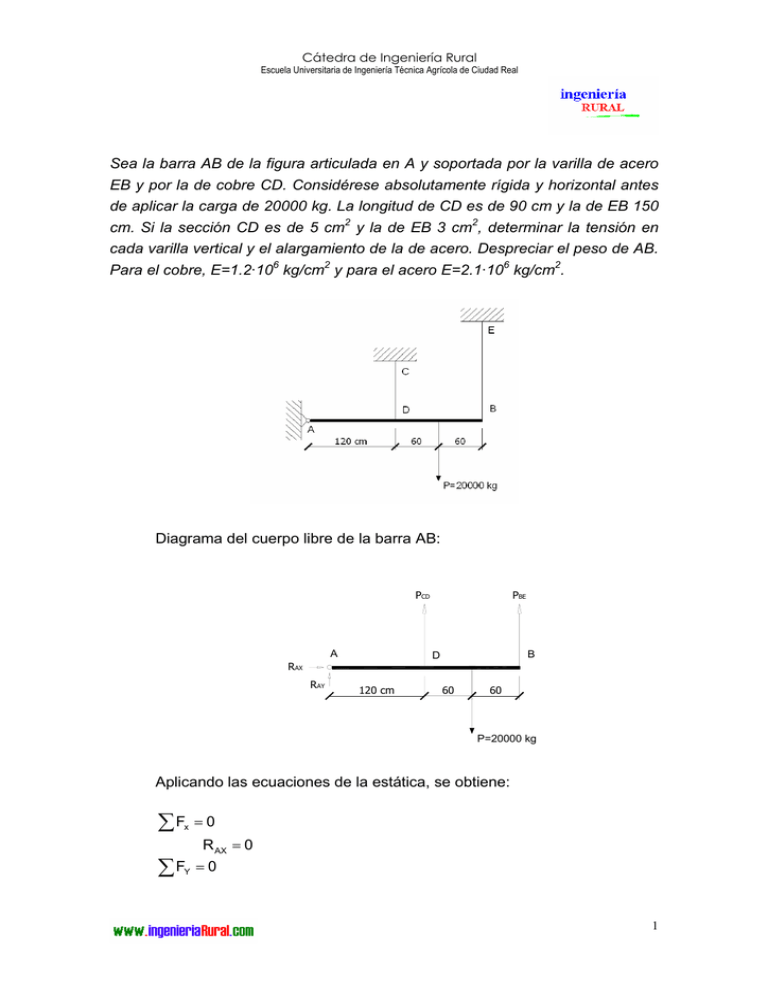
Cátedra de Ingeniería Rural Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real Sea la barra AB de la figura articulada en A y soportada por la varilla de acero EB y por la de cobre CD. Considérese absolutamente rígida y horizontal antes de aplicar la carga de 20000 kg. La longitud de CD es de 90 cm y la de EB 150 cm. Si la sección CD es de 5 cm2 y la de EB 3 cm2, determinar la tensión en cada varilla vertical y el alargamiento de la de acero. Despreciar el peso de AB. Para el cobre, E=1.2·106 kg/cm2 y para el acero E=2.1·106 kg/cm2. Diagrama del cuerpo libre de la barra AB: PCD A B D RAX RAY PBE 120 cm 60 60 P=20000 kg Aplicando las ecuaciones de la estática, se obtiene: ∑F x =0 R AX = 0 ∑ FY = 0 1 Cátedra de Ingeniería Rural Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real ∑M R AY + PCD + PEB = P A =0 120 ⋅ PCD + 240 ⋅ PEB − 20000 ⋅ 180 = 0 E C A B D CD EB 120 cm 120 cm Estudiando las deformaciones, se tiene δCD δ = EB → δEB = 2 ⋅ δCD 120 240 y aplicando la ley de Hooke: PEB ⋅ LEB P ⋅L = 2 ⋅ CD CD EEB ⋅ A EB ECD ⋅ A CD Teniendo en cuenta que LEB=150 cm, LCD=90 cm, EEB=2.1⋅106 kg/cm2, ECD=1.2⋅106 kg/cm2, AEB=3 cm2, ACD=5 cm2, se obtiene que: PEB = 1.26 ⋅ PCD lo que permite despejar las cargas que soportan cada varilla. 120 ⋅ PCD + 240 ⋅ 1.26 ⋅ PCD − 20000 ⋅ 180 = 0 2 Cátedra de Ingeniería Rural Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real PCD = 8522.7 kg PEB = 10738 .6 kg Por último, las tensiones de cada varilla son: σCD = PCD 8522.7 = = 1704.5 kg / cm2 A CD 5 σEB = PEB 10738.6 = = 3579.5 kg / cm2 A EB 3 3