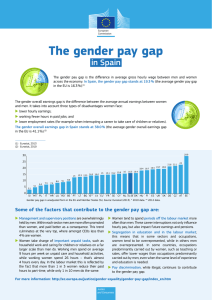
archivos de economía - DNP Departamento Nacional de Planeación
Anuncio

República de Colombia Departamento Nacional de Planeación Dirección de Estudios Económicos ARCHIVOS DE ECONOMÍA External Trade, Skill, Technology and the recent Increase of Income Inequality in Colombia Mauricio SANTA MARIA SALAMANCA Documento 171 10 de Diciembre de 2001 La serie ARCHIVOS DE ECONOMIA es un medio de la Dirección de Estudios Económicos, no es un órgano oficial del Departamento Nacional de Planeación. Sus documentos son de carácter provisional, de responsabilidad exclusiva de sus autores y sus contenidos no comprometen a la institución. EXTERNAL TRADE, SKILL, TECHNOLOGY AND THE RECENT INCREASE OF INCOME INEQUALITY IN COLOMBIA1 Mauricio SANTA MARÍA SALAMANCA. INTRODUCTION During the last decade there has been an increase in income inequality in Colombia, which has been particularly notable in urban areas. This development marked a departure from the trend observed from the beginning of the 60’s up to 1988, which showed consistent reductions in inequality (inequality increased in rural areas in the 80s). Since the growth of inequality coincided with an ambitious reform process, many analysts have concluded that the reforms are to blame for this unfortunate development (see Santamaría, 1997, 1999 for detailed descriptions of the reforms and the inequality developments). Despite the timing of these events, we will see two important things in this paper. First, the increase in inequality has been a very complicated process that has manifested itself very differently in the various parts of the income distribution, a fact that has been obscured by the tradition of summarizing inequality with a single number. For example, the left section of the distribution of earnings has not, in general, been negatively affected, but rather the most significant developments have occurred at its middle. Second, I will show that the connection between the increases in inequality and poverty and the trade reforms is at best weak2. This is reinforced by the fact that the timing of the two phenomena is not so coincident as it might seem at first. Instead, I will show that many of the most important changes in relative earnings can be explained solely by the interaction of supply and demand for different skill levels. The common view in Colombia that the rise in inequality is due mainly to the reform needs to be revised. This paper’s main objectives are thus to investigate the evolution of the distribution of labor income in Colombia during the previous 20 years and to identify the factors that lie behind this evolution. We attack the problem from two perspectives. First, we use a partial equilibrium model of the labor market to study developments related to the distribution of labor earnings of a homogeneous sample of individuals (homogeneous in terms of labor market attachement and geographical location), using skills as our primary tool of analysis. That is, a simple supplydemand framework for different dimensions and levels of skill is utilized to evaluate the role these variables played, and how they affected the distribution of labor earnings at different points 1 Very special thanks go to James W. Albrecht, Susan Vroman and Alejandro Mateus for their help, comments and expert guidance. I also want to thank Carlos Eduardo Vélez and Ana María Ibáñez for clever comments and other assistance. Finally, many thanks to the Banco de la República and the DNP for data and financial assistance. 2 A complete review of the literature pertaining to income distribution, structural reform and their relationship (not only for the Colombian case), can be found in Santamaría, 1999, and Cline, 1997. 1 in time. Second, we relate income to several demographical, skill and labor market factors, to isolate the effect these have had on the evolution of that distribution along the entire income range, and on other measures of overall dispersion and on skill differentials. We assess the merit of different explanations and quantify the contribution of each factor to the total observed changes. This second approach uses semi-parametric techniques that allow an analysis of the entire distribution, without assuming a specific parametric form. The difficulty of measuring the effects of trade on income distribution has been long recognized. It has created much debate (see the various articles in Collins, 1998, Cline, 1997 and Kosters, 1991). For this reason we avoid making causal arguments and restrict ourselves to measuring the degree of association between variables. This provides valuable information on the way that foreign trade interacts with earnings and skills. The paper is organized as follows. In the next section we study the changes in the distribution of labor earnings using a skill demand-supply framework, with skill defined by education, experience and gender. We begin by describing the data set and variables, and by discussing adjustments made to the data. The formal aspects of the model are also explained. The third section uses semi-parametric techniques to isolate the effects that several covariates had on the changes of the distribution of labor income. Robustness checks are presented when necessary. The fourth section concludes. SUPPLY AND DEMAND FOR DIFFERENT SKILL LEVELS3 Data The data used come from the ENH. Mostly, we worked with the national surveys of June 1978, September 1988, December 1991, September 1994, 1996 and 1998 (the qualification “mostly” refers to the fact that we carried out an exercise using additional surveys). My two main goals were (i) to construct a stable sample over time in terms of labor market attachment, and (ii) to extract information from the data that allows an investigation of the distribution of labor earnings from a perspective emphasizing supply and demand for different levels and dimensions of skill. Accordingly, we made several adjustments to the data and created new variables. To guarantee full comparability over time we restricted the urban sample to the seven cities that were present in all surveys. They accounted for 50% of the urban population in 1998 and are very heterogeneous in terms of location and socio-economic characteristics (they are Barranquilla, Bucaramanga, Bogotá, Manizales, Medellín, Cali and Pasto)4. In rural areas all four regions defined in the survey were used. Additionally, I deleted observations according to the following criteria. First, I deleted the inactive and unemployed. Second, those who stated that they were employed but reported earnings of zero or did not report earnings were discarded. Third, we deleted all observations for which the variables education, age, gender, sector of economic activity and occupation were reported missing or outside the coding provided by DANE. Finally, 3 This section draws from Katz and Murphy (1992, KM hereafter), Bound and Johnson (92), and Murphy, Riddell and Romer (1998). 4 In the 1978 survey the coding of the metropolitan areas changed and thus we resorted to other methods to identify the seven cities. Although I am confident of the outcome of this exercise, some “leakage” may have occurred and some observations from other cities may have been included or vice versa. 2 I discarded all workers that reported working less than 20 hours a week. After these adjustments, the size of the weighted samples ranged from 3.400.000 workers in 1978 to 5.400.000 in 1998 (weighted means adding the sampling weights included in the ENHs). These final samples include the self-employed. Although the purpose of exercises like this one is to measure the price that the labor market assigns to different skills and that these prices are better captured by wages than self-employment income, the latter depends on the skill of the recipient and including these earners is especially important when trying to investigate the effects of international trade. Several studies (e.g. Vélez, Bouillon and Kugler, 1999) have demonstrated that while selfemployment earnings display higher inequality than labor income, their dynamic behavior and variation by skill level are very similar. The measure of earnings used is the monthly sum of labor and self-employment incomes. Finally, the trade, GDP and price data come from the annual statistical bulletin published by DANE, while the exchange rate information was taken from the monthly magazine made available by the Banco de la República (Central Bank). Exchange rate information is needed to convert trade and GDP information to a common currency. Methodology Skill is proxied by education, potential experience and gender. Education was taken directly from the ENHs and is measured in years. Experience was constructed as exp=min[(age-education-7), (age-12)], where age is as of the time of the survey. I divided the population into 48 cells in the urban case (2 genders times 6 education groups times 4 experience groups), and 24 cells for rural areas (2 genders times 4 education groups times 3 experience groups). The urban educational categories are uneducated, primary (1-5 years), high school dropouts (6-10), high school (11), some college (12-15) and college or more (16 or more years), while the experience groups are 0-5 years, 6-10, 11-24 and 25 or more years of potential experience. For rural areas the corresponding groups are no education, primary (same definition), high school (6-11 years) and college (12 or more years) for education, and 0-10 years, 11-24 and 25 years or more for experience. Then, we computed the relative labor supply provided by each cell (si) as the ratio of the number of workers in the cell to the total number of observations for each year (weighted by the sampling weights). Finally, the average supply for the 1978-98 period was computed for each cell. This quantity is the fixed weight that we use throughout this section to compute earnings for more aggregated groups, such as educational or gender groups. That is, earnings for those groups are calculated using a fixed weight aggregation procedure, according to the following equations. The fixed weight fi for cell i, i=1,…,n, n=48 or 24 is defined as fi = ∑s t T it t = 1978, 79,..... with ∑ i fi = 1 where T is the total number of years in the sample. Earnings (w) for the more aggregated group j in year t in turn are given by 3 w jt = ∑ ∑ i∈ j f i wit i∈ j fi Thus, in effect we are comparing earnings for a fixed skill composition of the population. In this way we avoid confounding pure earnings movements with changes in the composition of the labor force that may influence earnings behavior5. Finally, a word related to trade, GDP and price deflation. The trade variable was created as the ratio of net imports to GDP for the 23 two-digit sectors included in the ENHs. Then, each observation was assigned an import coefficient based on its sector of employment. The trade and GDP data were converted to a common currency using the average nominal exchange rate (pesos/US$) for the year in question. Income was deflated to pesos of 1978 using the CPI for each of the seven cities to cope with differential price movements across regions. Evidence We begin with the evolution of the distribution of labor earnings across (between) skill categories. Table 4.1 and figures 4.1 and 4.1a summarize data on changes in urban earnings for different skill groups of the population, distinguishing absolute (percentage change of mean income of each group) and fixed weight changes6. The differences between these two measures show what part of the changes was caused by shifts of the skill composition of the labor force. Thus, the fixed weight measure is more accurate in reflecting pure earnings changes. For ease of presentation, we further aggregated the educational groups into low education (uneducated plus primary), medium (high school dropouts, high school and college dropouts) and high education (college or more). The criterion used to choose these coarser aggregates was the observation of how close the earnings of the finer groups moved through time. In the graphs every group’s earnings are normalized to one in 19787. The tables and figures referenced above show that all education groups improved their situation along the entire period. The gains for the low and medium educated came mainly before the 1990s, while the highly educated lost over that period but gained in the final decade. During the 1990s all educational categories enjoyed rises in absolute earnings, the most for the highly educated group (38.7%), and the least for the low 5 We also computed average earnings for each cell and a relative earnings index for it based on the ratio of its average earnings to the overall mean earnings. Then, we multiplied the average supply of each cell by this index, obtaining what KM call supply in efficiency units, which amounts to a fixed weight aggregating scheme increasing the weight of the richer cells. Results for both procedures will be shown when we feel that it is worthwhile. For the most part, however, they will be reported for the first methodology 6 It is important to clarify that the graphs in this section were computed obviously using the 6 years of the data (1978-88-91-94-96-98), but they were drawn for the entire period 1978-98 for presentation purposes. 7 We computed also a predicted change from a regression of the log of earnings on several covariates (47 dummies for the skill cells, education and experience within them, experience squared, sectoral affiliation, occupation, 6 dummies for the cities, and profession). These predicted changes are quite close to the actual ones for the 1978-88 and 88-91 periods, but then during the 1990s the regression lost power (the predictions differ by a larger amount from the actual changes, and in many instances even the signs differ). That is, starting in 1991 unobservables began to play an important role in earnings formation. Moreover, the discrepancies are consistently larger for higher levels of skill, indicating that this phenomenon is affecting the high skilled disproportionately. 4 education group (8.3%). However, this change in the 1990s occurred completely from 1991 to 94 for the two lower groups. Fixed weight changes were especially large among the low and high education groups for the entire period (17.5 and 14.4%), and negative for the intermediate category (-3.9%), while in the 1990s college individuals’ fixed weight earnings increased by 37.6%, and the low and intermediate groups individuals’ by 8.5%. Hence, we conclude that earnings for the intermediate education group have eroded significantly, while the two remaining categories have experienced growing earnings, but over different periods. One important point is that the absolute and fixed weight changes are almost identical for the low education group, and very different for the other two categories. In the case of the intermediate one, the fixed weight measure is significantly lower than the absolute one, while the opposite is true for the highly educated. This is the first indication of a point that will be central throughout the paper: supply of intermediate education has been growing “too fast”, while that of high education is not augmenting fast enough. Table 4.1 reveals that the gains for the highly educated in the 1990s were larger among women. While college educated women experienced fixed weight earnings growth of 55.7%, among men this figure reached only 30.8%. In fact, for the whole period (1978-98), highly educated women enjoyed the largest positive change in absolute earnings (38.5%). For the two remaining categories the growth in fixed weight earnings was also larger among women. Absolute changes for women between 1991 and 98 ranged from 19.5% (intermediate) to 59% (college). The female group that benefited the least during the 1990s was the intermediate one. Among men the three categories displayed almost identical absolute earnings changes for the entire period, while the fixed weight measure shows the intermediate category as the clear loser, with a decrease of 5.7%. Replicating the pattern observed in the full sample, highly educated women experienced all their gains in the 1990s. Highly educated males began to experience larger earnings growth than the rest of the population since 1988, but females’ increases during the 1990s were more than enough to outpace them. Finally, the intermediate category among men and women endured falling fixed weight and absolute earnings in most of the sub-periods. Thus, educational earnings differentials followed similar qualitative patterns, but the magnitude of the changes was different for the various categories. Figure 4.1b depicts the evolution of the fixed weight log differentials of each category against college graduates for the period 1978-98, normalizing them to one in 1978. The differentials were reduced between 1978-88, and then a monotonic increase started in the latter year and was maintained until the end of the data, especially for the college-intermediate differential. This graph reinforces the message expressed in the previous paragraphs: high-school dropouts and completers were the groups that lost the most, while low educated individuals actually gained on college ones (the differential in 1998 was slightly less than in 1978). Women’s earnings grew more than men’s during the 20 years. Indeed, while men earned on average 63.3% more in 1998 than they did in 1978, this figure was 85% for women. These quantities translate into fixed weight changes of 1.6% for men and 15% for women. This also applies for every subperiod but 1988-91. Gender differentials by education level are depicted in Figure 4.1c. In the educational category in which the gender differential fell the least was the intermediate one, which had the lowest differential in the initial year. In the last year of the data, the gender differential was practically indistinguishable between low and intermediate educated individuals, and it had decayed by more than 0.2 log points among highly educated ones. This fall, however, occurred almost completely during the period 1994-98. Looking at the changes by experience groups, one notices that this variable did not play a 5 significant role in the evolution of labor income inequality. That is, changes in earnings for the three groups presented in Table 4.1 do not show a detectable pattern, especially during the 1990s. The only salient feature is a trend towards a deterioration of the relative position of the older cohorts. Younger cohorts of women with a high school degree or less benefited the most during the 90s. At higher levels of education the situation is the opposite: older cohorts enjoyed the highest earnings increases in the 1990s. Among men the pattern was similar but the differences between experience groups are not so easily inferred. Notwithstanding this, a generalized earnings increase for younger males can be detected for the two lower educational groups, while older workers tend to do better in the more educated categories. The changes in absolute mean income for the entire sample were 71.7% along 1978-98 and 35.5% for 1991-98. This 71.7% breaks down to 31.9% in 1978-88, -4% for 1988-91, 31.2% during 1991-94, -8% for 1994-96 and 12.2% for 1996-98. Looking at fixed weight changes and thus removing the effect of shifts of the skill distribution, we find that it reached 5.7% for the whole period, which occurred entirely during 1991-94. Indeed, from 1978 to 1988 fixed weight earnings fell by 0.8% and a further decrease was observed in 1988-91 (-8.7%). During 1991-94, the change reached 28.6% to fall by 9.2% in 1994-96 and by 0.2% in the final period8. We summarize the evolution of labor income inequality in Figure 4.2, which shows the log differentials between the 90th-10th, 75th-25th, 90th-50th and 50th-10th percentiles of its distribution for the six years analyzed (normalized to one in 1978). Several important facts can be extracted from this graph. First, inequality began to rise somewhere between 1988 and 1991. Moreover, this pattern became steeper and affected the entire distribution between 1996 and 1998. Second, the increase in inequality has been driven by a rising dispersion above the median and not by relative income decreases in the left tail of the distribution (the first decile). Finally, reflecting the fact that the high-school categories experienced large earnings reductions, the most substantial increase in inequality occurred between the 25th and 75th percentiles. Table 4.2 displays information about average earnings by decile, reinforcing the message that the highest and lowest deciles have been the most favored (deciles 8, 9,10 and 1). To end the discussion of the urban data, we proceed to study the evolution of within group earnings dispersion. Up to this point we have been concerned with inequality between groups. To study this component we ran a regression in each year of the log of earnings on 47 dummies corresponding to the skill cells (47=48-1 reference cell), experience squared, its interaction with gender and linear terms for years of education and experience within each cell. The residuals from this regression capture inequality within each group, i.e. they capture the effect on labor income of variables unrelated to the three skill dimensions used. Results are shown in Figure 4.2a, where the same log percentile differentials of the predicted earnings are depicted. Residual inequality began to increase between 1988 and 1991 everywhere in the distribution, and this rise continued until 1998. Furthermore, starting in 1996 the growth in residual inequality increased. This indicates that not only has the relative situation of high school individuals worsened, but also within this group differences have been growing, even more than the ones observed between groups (measured by the evolution of mean earnings of each skill cell). To put these changes in perspective, the rise of residual inequality has been larger than the changes that can be explained by gender, education and experience combined. 8 The changes reported are very similar to the ones computed using efficiency-units weighting. 6 To conclude, we observe a mixture of equalizing and unequalizing developments in urban areas, and two sub-periods that are clearly differentiated. We found a reduction in the differential between the least educated and the college educated workers, an improvement of the relative position of younger entrants to the market, and earnings gains for women. On the other hand, we found a worsening of the relative position of intermediately educated individuals with respect to the rest of the population (especially to college workers), and relative income gains for the more experienced workers during the 1990s. Over time, 1978-88 was a period of reduced inequality between groups, while after 1988 the opposite happened due to the rise in earnings of the highly educated. Also, during the latter period experience differentials grew among the highly educated, meaning that the unequalizing effect of this group was reinforced by this experience effect. Now we turn our attention to rural areas, which we divided into 24 cells as explained above. In contrast to urban areas, the predictive power of the regression used is poor (see footnote 6). This indicates that the rural labor market is not as strongly governed by observable skill measures as the urban one is. It seems that the price of labor in this market responds to other variables, such as the conditions of the product markets, which are not captured by traditional skill analysis. Table 4.3 shows the between component of earnings changes. The group with the lowest education (0 years) fared better than the rest of the population, both for the entire period and during the 1990s. The fixed weight change in earnings for this group reached 33% for the full period and 4.5% for the last decade, in which they were the only ones who enjoyed positive earnings changes. For the high school dropouts and graduates the reductions were close to 8 and 46%, and the highly educated (more than high school) experienced an increase in the whole period of 33%, but a sharp reduction over the 1990s of 22%. Looking more closely, we find that the uneducated individuals only suffered losses between 1988 and 91, while the highly educated ones reduced their earnings in the period 1991-96. These fixed weight shifts translated into absolute earnings gains over the entire period for the uneducated (36%), primary (8.5%) and highly educated (6%), while the high school group ended up earning 4.2% less in 1998 than they did in 1978. Within the uneducated group, the younger cohorts’ (0-25 years of experience) enjoyed fixed weight earnings changes greater than those observed among older workers (23 vs. 15.5%). This constitutes a generalized pattern across educational groups of both sexes. Thus, the older high school workers endured the greatest losses in earnings (almost 65%). It is not difficult to infer that women did better than men all along the 20 years. Women experienced fixed weight earnings changes of 37% for the entire period and of –5.1% during the 90s, while these figures were 4.5 and –34% for men. In absolute terms men were earning 20% more in 1998 than in 1978, and 36% less than in 1991. Women’s earnings were 50% higher in 1998 than in 1978 and 4% smaller than in 1991. The developments related to education and experience are homogeneous across genders. As a consequence, the groups who benefited the most during the 90s were young women of any educational category (especially uneducated), older women with college education, and young uneducated men. The left-behind groups were all the older men but the uneducated, and within these, the high school ones endured absolute losses of more than 42%. The absolute changes in mean income for the entire sample were 22% for the whole period and 31% for 1991-98. This 22% breaks down to 57% in 1978-88, 12% for 1988-91, -14% for 199194, -30% for 1994-96 and 14.3% for 1996-98. Fixed weight changes were of 9% for the entire period and close to –30% in the last decade. Periods of positive growth were 1978-88 (43%), 7 1988-91 (10%) and 1996-98 (15%). From 1991 to 1996, the negative change reached 39%. We summarize the changes of rural labor earnings with the evolution of the same percentile differentials used in the urban case, presented in Figure 4.3. The period 1988-94 was one of negligible changes in inequality as described in Santamaría (1999). Also, from 1978 to 1988 we observe a deterioration of rural earnings, especially for the poorest segments of the population. There was remarkable stability in the distribution of earnings above the median and below the top 10%, for the 90th-50th differential displayed virtually no change. Finally, starting in 1994 inequality increased significantly. It is evident that the lowest 10% of the distribution suffered huge losses between 1994 and 96 (evidenced by the jumps of the 90th-10th and 50th-10th differentials), and then they somewhat improved their situation during 1996-98. The 75th-25th differential displays continued growth since 1994, reflecting the losses endured by the high school educated individuals. We wrap up this section with a brief comment related to the within component of inequality presented in Figure 4.3a. It is evident that residual inequality followed the same pattern as the observed one, i.e. the least lucky within the lowest deciles of the overall distribution (who are among the older cohorts of high-school individuals), endured great losses during the period 199496, while the luckiest individuals in low deciles were able to at least maintain their situation. Finally, what is clear from the discussion above is that the increase in inequality in rural areas is not linked to rising prices of higher skill levels, as defined by education, experience and gender. Possible Explanations In this section we try to explain the changes in the distribution of labor income described above using a simple model that highlights the interaction of supply and demand for different levels of skill. The model I develop is in the spirit of the one proposed by KM. It assumes a concave aggregate production function for each of J sectors that comprise the economy. The inputs are the different skill types of labor, indexed by i (i=1,…, I). The production function is assumed to be CES. Thus, Yj = (∑ a N ) i 1 γ γ ij ij (1) Where Yj is output in sector j, Nij is the number of individuals of skill category i employed in sector j, aij is an unobservable technological parameter for skill group i in sector j, and γ is the elasticity of substitution among skill groups. The marginal conditions for each sector are p (∑ a N ) j i ij γ ij 1−γ γ aij N ijγ −1 − wi = 0 where pj and wi stand for the price of sector j output and the competitive wage for skill i, respectively. The demand for skill group i in sector j is thus given by 8 aij p j N ij = wi 1 1−γ Y j (2) Differencing and assuming that real wages are fixed we get aij p j dN ij = wi 1 N 1−γ dY j = ij dY j Yj (3) Summing over j on both sides of (3) we obtain ∆Di = ∑ j N ij dY j (4) Yj The quantity ∆Di gives the weighted sum over sectors of changes in employments for skill i with weights given by percentage changes in sectoral output. Thus, it measures the change in demand for skill group i that would take place at fixed factor and output prices as a result of shifts in the industrial composition of the economy, caused, for example, by technical change. We follow the tradition in the literature (see for example Freeman, 1975, 1980; KM and Juhn, Murphy and Pierce, 1992) and implement this index proxying the sectoral change in output by the change in total factor inputs. The reason for doing this is twofold: first, I want to avoid complications related to the correct value added measurement of sectoral outputs, and second it is not possible to get information on sectoral outputs that matches the support of the index j (see the paragraph after the next). Thus, the demand shift index is computed as ∆Di = Ni ∑ j µ ij ∆N j Ni , µ ij = N ij Nj (5) We measure µ ij as the average share of workers of skill group i in sector j over the entire period. Additionally, we divide by Ni to express the change in demand relative to the fixed weight employment share of skill group i in the base period (Ni is the average share of skill i in total employment). Note that all quantities involved in (5) are equilibrium quantities and directly measurable from the data at hand. Initially j indexes 165 industry-occupation “sectors”, made up of 33 industrial divisions times 5 occupations (blue and white collar, domestic employee, self-employed and employer)9. The 9 The 33 sectors are: agriculture and hunting; lumber extraction; fishing; coal extraction; oil and natural gas extraction; metallic minerals extraction; other minerals; manufactured food products, beverages and tobacco; textile and leather industry; lumber industry; paper products and publishing; chemical products; production of non-metallic goods; basic metallic products; other metallic products; other manufactures; 9 quantity in (5) corresponds to the fixed weight manpower requirements index proposed and further developed by Freeman (1975, 1980). Intuitively, this index tells us that inputs employed mostly in expanding sectors will experience increased demand, while the demand for factors used in contracting sectors will fall. As can be seen in equation (3), when ∆Di N i is not computed using fixed input prices, it gives a biased measure of true demand shifts. This is because under the fixed input prices assumption skill groups that experienced real wage increases would show higher growth in their relative demand than the one given by applying (5) directly. That is, changes in wages affect the distribution of sectoral outputs. Since we work with changes in sectoral output (or its proxy) that already occurred in the presence of non-fixed wages, ∆Di N i is biased. True demand shifts are generally higher for skill groups with increasing wages, and lower for those that endured wage losses (for an alternative derivation of the index measured in efficiency units see KM). Within the confines of our model we try to construct a more exact measure of the true demand shifts by noting that with constant input prices (5) is the correct measure, but since we are not controlling for changes in wages when we apply it, we are really computing the following quantity (still assuming fixed output prices), ∆Di* = ∆Di − 1 1−γ dwi wi N i (5a) This comes from differencing (2) letting w vary, making some substitutions, and summing over j on the final expression. Thus, for elasticities smaller than one, we underestimate the true demand shifts for skill groups with rising wages. We implement this corrected measure when necessary, making it clear in the text, using an estimated value for the elasticity of substitution that comes from a regression specified below. If we want the true shift, for example, for a skill category whose wages grew, we should add to (5) the second term in the r.h.s. of (5a). Total demand for labor in skill category i is obtained by summing over j in both sides of equation (2) Di = ∑ j ∂Di = ∂wi aij p j wi 1 2 −γ 1−γ i (γ − 1) w 1 1−γ Yj ∑ (a j (6) p j )1−γ Y j 1 ij (7) Equation (7) tells us how the demand for a skill type varies with its own wage. We assume that the supply of workers of each skill is predetermined at each point in time by past schooling, etc, so the demand schedule becomes a wage determination equation, and shifts of the supply curve move wages accordingly. For this system to be stable we require the quantity given by (7) to be negative, which amounts to the requirement that the elasticity of substitution be less than one. electricity and gas; water; construction; retail commerce; wholesale commerce; restaurants and hotels; transportation and storage; communications; banking; insurance; real estate; public administration and defense; health services; other social services; enjoyment services; domestic services, and international organizations. 10 Finally, we assume full employment for each skill group N i = Di , so ∆D dN dwi = (1 − γ ) i − i wi Ni Ni (9) According to (9) percentage changes in own wages should be negatively related to percentage changes in net supply. Thus, to test the hypothesis of whether the observed changes in earnings are fully explained by skill supply and demand interaction I estimate equation (9) and consider that the changes are explained by the model if the elasticity of substitution is less than one (i.e. if the regression coefficient is statistically greater than zero)10. If that is not the case, we conclude that the data are not consistent with such a model and some other factors (technical change, for example) are playing a major role in the determination of earnings. We estimate (9) for each period using three different demand shifts indices. First, the one given by (5) (the biased one), and then we use equation (5a) with two possible values for γ chosen in an iterative manner. First we recover the estimate of the elasticity from the previous estimation and re-estimate (9) using the corrected demand measure computed with this recovered value. Then we repeat this exercise once more utilizing the second estimation value of γ . Since testing the hypothesis of the regression coefficient being greater than zero is not possible in practice (because the t statistic really informs us as to whether the coefficient is statistically different from zero), the main statistic we use is the 95% confidence interval for the estimated coefficient, which allows us to infer with 95% of probability whether the elasticity of substitution is less than one or not. Table 4.4 presents the results of estimating (9) for the three proposed scenarios. Equation (9) is estimated using weights equal to the average share of each skill group over the 20-year period The Table tells us that supply and demand shifts are able to explain the changes in wages for the periods 1978-88 and 88-91, while they fall short during 1990s, especially 1996-98. During the first 6 years of the decade the results are ambiguous. Additionally, the periods for which the differences among estimation results using the alternative demand indices is greatest are 1978-88 and 1994-96, which correspond to periods in which the economy was subject to important exogenous shocks, as explained below. We complement Table 4.4 with Figure 4.4, which we borrow from KM with some modifications. Each panel in this figure plots the percentage changes in earnings versus net demands for our 48 skill cells and for each sub period, and additionally we fit the regression line coming from estimating (9) using the biased demand measure. Figure 4.4 confirms the results provided by Table 4.4, but offers some additional information. First, in the period 1978-88 the supply-demand framework does not explain the observed changes in earnings well. During that period very large changes in the skill composition of the Colombian population took place, especially in educational attainment and female participation rates. In addition, the economy went through a 10 More specifically, this test will indicate whether the observed changes in earnings are consistent with a model of earnings determination in which demand is negatively sloped (gamma<1) and constitutes a wage determination schedule, and supply is a vertical line predetermined by exogenous factors. 11 recession from 1981 to 84, followed by a severe adjustment program and an important recovery during the period 1986-88, helped by the coffee boom that started in 1986. The second comment related to Figure 4.4 refers to the 1991-94 period. The poor fit of the regression seems to be driven by outliers, calling for a more detailed look. We finish with an additional exercise. The estimations may be contaminated by spurious components coming for example from technological progress or changes in the size of the economy (which most likely create linear trends within cells). To cope with this problem, we re-estimate (9) in second differences. The results are presented in Table 4.4a. Note the switch in the sign of the regression coefficients for the periods 1991-94 and 94-96. Once the cell-specific trend is removed from the regression, changes in net demand for the various skill levels are able to explain shifts in earnings for the interval 1978-94. For the second part of the 1990s they are not able to do this. In summary, changes in supply and demand for different skill levels are enough to explain shifts in earnings of finely defined skill groups all along 1978-91, they do so in a weaker manner during 1991-94, and they fail to explain earnings changes in the second half of the 1990s. Earnings changes in this period are more likely explained by macroeconomic shocks and technical change. The latter is consistent with the difference in the estimation results between the raw and detrended series. Several robustness checks were carried out for this exercise. First, we estimated equation (3) of the KM paper, which shows that changes in wages and net supply must negatively covary. We estimated this equation using both efficiency units weighting (as KM do in their paper) and fixed weights. The results confirm that earnings changes are explained by shifts in net demand over the period 1978-91, while for the latest period of our data (1996-98), exogenous factors altered the interaction among prices and quantities in the skill market significantly. Additionally, for the two intermediate intervals, 91-94 and 94-96, the results weakly accord with the coefficients from the first regression above. This observation, combined with the fact that for these two periods we obtained different signs depending on the specification used in the previous estimation, lead me to conclude that changes in skill composition and demand are not enough to explain earnings changes in this period. Second, I carried the same three estimations for samples including only people that worked more than 30, 40 and 48 hours a week obtaining exactly the same results (48 hours a week is the legal definition of full time in Colombia). Finally, I repeated the exercises for hourly wages, exercise that marginally reinforced the results11. We next look in more detail at the changes in earnings, supply and demand for the finer skill groups. In Table 4.5 the first column shows the change in supply ( ∆S ), the second the demand shift (5), the third the change in net supply ( ∆NS ), and the final column shows the change in the log of fixed weight earnings. The variables are computed as 11 The reason why I do not use hourly wages as my variable of analysis is simply that there are too many observations for which this variable is missing in the ENHs. Additionally and in contrast to the US, in Colombia wages are set monthly and not hourly. I believe that monthly earnings are a better measure than hourly wages of the price of labor in Colombia. Notwithstanding this, I repeated the majority of exercises presented in the paper for hourly wages and the results are almost identical. I notice that they are somewhat reinforced, especially the one related to the increases of wages of highly educated individuals in the 1990s. 12 N ∆S i = Ln i ,t Nt N − Ln i ,t −1 , N t −1 ∆NS i = ∆S i − Ln(1 + ∆Di ) Table 4.5 shows that the supply of college-educated workers grew over the whole period, especially among women, while that of uneducated and primary individuals shrank. One point that will be crucial later is that the bulk of these shifts occurred between 1978 and 88. Looking at the relationship between changes in earnings and in net supply for educational groups, we find that they agree with the model discussed above, except for college and high school dropouts (weakly for the latter). Demand for uneducated individuals fell over the entire period, but the reduction in supply was so sharp that their net supply was reduced by 1.34 log points, allowing their earnings to go up almost 30%. A similar pattern can be observed for primary educated individuals. These developments were essentially the same for all sub periods. Demand growth for high school workers can be characterized by sluggish (at best) all along 1978-98. At the same time we observe a huge increase in their supply. Thus, the fall in high school graduates’ earnings can be completely explained by the increase in their net supply. High school dropouts, on the other hand, displayed a fixed weight earnings reduction of 5% in the presence of no change in net supply. Finally, college individuals enjoyed growing demand in every period that accumulated to more than 31% from 1978 to 1998. However, this was not enough to offset the rise in supply commented above. Their earnings increased by 0.13 log points despite growth in net supply of more than 130%. For the 1990s we can reproduce exactly the same comments, except for the fact that net supply of high school dropouts fell abruptly. The negative association between net supply and earnings for educational-gender groups for the entire period is exact for men (except college), while among women it does not hold for high school, college dropouts, and college. Earnings of female workers increased all along the 20 years, despite growth in their net supply. Hence, we have two unexplained phenomena: the growth in earnings of college educated individuals and women, which took place even when net supply was growing fast. Next, we look at the changes in earnings and quantities for each sub period. For the period 197888, the negative correlation between changes in earnings and in net supplies is almost exact, even for college graduates. The exceptions are men and women in the aggregate. For these groups, however, relative changes in earnings (relative to the fixed weight mean) are in accordance with the movements in quantities. The period 1988-91, as we saw, was one in which the tests carried out above showed that the movements in earnings could be explained by changes in net supply. The information contained in Table 4.5 displays a generalized fall in earnings for every group. Notwithstanding this, relative earnings changes are in the right direction. Similar patterns can be detected for the next two periods, 1991-94 and 94-96. In the first, the changes in earnings were positive for all splits, but the relative changes show a general negative correlation with shifts in supplies. The caveat is that the growth in net supplies for the highly educated were large, and their positive changes in earnings were even larger, especially for women. This is the reason why we found that net supply movements were not able to explain earnings changes in this period. In the latest years all the groups show the changes in fixed weight and relative earnings going in the same direction as changes in net supply. Up to now the demand index (5) has been computed with j indexing 165 industry-occupation cells. Thus, it reflects the shift in demand for different levels of skill that occurs between those partitions due to changes in the cell composition of the economy. If we instead let j index only 13 the 33 industrial sectors and calculate (5) again, we will obtain the shift in demand that takes place between them. The difference between these two measures gives us an estimate of the demand shift that occurs within industrial sectors and between occupations, the “within” demand shift index. These computations are presented in Table 4.6. The total measure shows that the rate of growth of demand for the more educated workers decreased from 1988 to 1994 and accelerated again during the second half of the 1990s. However, this increase in demand can be best characterized as growing at a quasi-constant yearly rate. The yearly average of demand growth for this type of individuals was close to 1.6% between 1978-88, and then decreased to 0.9% during the next six years. Starting in 1994 it went back to levels close to those observed in the initial period. Thus, demand for college educated workers increased by 30% during the entire period, and 12.5% during the 1990s. This increase in demand came mainly from the within component, especially during the periods 1978-88, 91-94 and 96-98. This element accounted for 18 of the 31 points of the overall increase in demand for the entire period, and for 4 points out of the 12 during the 1990s, due its negative growth of 1994-96. Thus, for the this three periods demand for highly educated individuals came from within the sectors in which they were already employed, shifting them between occupations, fact that constitutes evidence supporting the presence of factor biased technological change favoring high levels of education. High school individuals endured sluggish growth in demand from both the between and within components, reinforcing the statement made before that it seems that their poor earnings performance is explained completely by the behavior of net supply. Even demand for uneducated individuals grew more during the 90s than the one for high school workers. Primary educated workers experienced reduced demand mainly from the between component. Uneducated individuals endured large reductions in demand for their services during the earlier period, with the bulk of the change arising from the within component. This comes entirely from female workers, reflecting the decrease of the relative importance of the domestic service occupation. In effect, 18% of women were employed in this occupation in 1978 (31% of the uneducated), while this figure was 9% in 1998, (23% of the uneducated). The same comments can be extended to the primary educated women. Finally, demand favored women over men by 5 percentage points approximately over the entire period, but the shift in this variable was larger for men during the 90s (0.1 vs. –0.6%). This last development took place entirely between 1991 and 1994, when demand grew 4% more for male than for female workers. The between component was invariably negative for men all along the 20 years (except during 1991-94), but it was compensated by positive within shifts in some periods, due to the movements observed among highly educated men. For women, the situation was the opposite: positive between changes to some extent offset by negative within shifts. Thus, demand for female workers increased because expanding sectors used women more heavily than shrinking ones, but declining female intensive occupations like domestic service partially offset this increase. The expanding sectors were banking, insurance and commerce. The average share of female labor in the first two was 55%, while in the latter it was 51%. The abnormal behavior of the period 1991-94 is explained by the high growth of the male intensive construction sector. Changes in Relative Demand Arising from International Trade Flows: In the last section we learned that the growth in earnings of college educated individuals and women cannot be explained by changes in relative supplies combined with shifts in demand arising from changes in the industrial structure of the economy. Thus, in this part we examine whether flows of external trade of goods and services can help us explain those developments. For this purpose we rely on 14 the factor content (FC) approach to the subject which, simply put, tells us that imports bring into the recipient country the workers used to produce the goods, effectively adding them to the native supply. Exports, of course, are thought to do the opposite (for detailed treatments of this statement see for example Murphy and Welch, 1991; Cline, 97; Freeman, 98; Santamaría, 99; Deardorff and Staiger, 88 and Krugman, 95). In this sense, this model constitutes a natural extension of the one used above. Given the postulates of the FC model, the change in endowments for different levels of skill arising from trade, can be computed using the same logic used to calculate changes in relative demand due to shifts in industrial composition. Hence, we need to multiply skill coefficients for each sector by net imports in that sector to obtain the change in labor demand for the particular level of skill that occurs due to actual trade flows (note that this is done at fixed wages and thus we need not to worry about changes in earnings affecting demand). Keeping the notation used above, we measure the net supply of workers of skill level i embodied in trade in any period by the following quantity (relative to the entire labor force with the latter normalized in each year to sum to one). NM stands for net imports measured in dollars NM j STi = ∑ j µ ij N j Y j (11) The results of applying (11) are shown in Table 4.7. The implicit supply of workers of all types has always been positive, i.e. Colombia has been a net importer of workers in the last 20 years. As expected, implicit supply increased for every skill group between 1991 and 94, with the aggregate increment larger than 200%. We also compute relative demand shifts due to international trade. The measure used was proposed by Murphy and Welch (1991) and developed by KM. ∆DTi = − 1 Ni ∑ NM j µ N ij j j Y j NM j +∑ Nj j Y j (12) There are three differences between (11) and (12). First, the supply measure is divided by the average share of skill level i over the entire period to make the index reflect the change in demand relative to the fixed weight distribution of employment. Second, (11) is multiplied by minus one to turn it into a demand measure. Finally we add the second term, which corresponds to the weighted overall trade deficit (the weights being sectoral employment distributions), turning the index into a relative one (i.e. it subtracts from the change in demand for each group the overall change in demand arising from the trade deficit). The calculations for equation (12) are presented in Table 4.7a. That Table shows that the demand shifts are in the right direction to explain earnings changes, but these shifts are too small to counteract the changes in supplies, even in 1994, when the demand shift measure increased substantially for all groups12. We 12 Since trade flows in services suffer from measurement error, we computed the demand index restricting the sample to the agricultural and manufacturing sectors to see if the measures computed on the entire sample were biased downwards. These calculations show that indeed the demand indices increased for all skill categories, but they still were very small and the order of magnitude of the numbers was not greatly altered 15 conclude that demand shifts induced by external trade flows have not exerted an important effect on earnings for the different levels of skill, although they have contributed to a small extent to the widening of the educational wage differentials between highly and intermediately educated workers. However, the additions to the native supply made by the implicit number of workers embodied in such flows seem to be more important quantitatively and also display a qualitative pattern compatible with the observed earnings changes. Hence, our next exercise will explore this issue more deeply. - Trade, Technology and Education: Here we explore the relationship between education, technology and relative earnings on one hand, and trade, education and relative earnings on the other. Thus, we need a simple method to test the presence of factor biased technical change, meaning a flexible model that permits different factors to be affected in diverse ways by technical change. For the second part, the model should incorporate the interaction between relative supplies and earnings. I use the model proposed by Murphy, Riddell and Romer (1998, MRR hereafter). Production is assumed to be Cobb-Douglas with two inputs, capital (K) and labor (B). The latter is partitioned into skilled (H) and unskilled (L) with a CES aggregator. Thus, [ ] 1 γ γ B = λ ( A(t ) H ) + (1 − λ )(B(t )L ) γ [ (13) Y = K α B (1−α ) ⇒ Y = K α λ ( A(t ) H ) + (1 − λ )(B(t )L ) γ γ (1−α ) ] γ (14) Through the functions A(.) and B(.) the productivity of both types of labor is affected differently by technological progress. Using the first order conditions for profit maximization and letting gi(t)=ln[A(t)] for i=A,B we get W H ln H (t ) = a + γ [g A (t ) − g B (t )] − (γ − 1) ln L WL (15) Following MRR, we impose the restriction on (15) that the growth of the difference in productivity changes for both inputs is linear. Thus, W H ln H (t ) = a + γgt − (γ − 1) ln L WL (16) for some constant g. If the second term on the r.h.s is not zero, then technical change affects each labor type differently, i.e. their technological efficiencies grow at different rates over time. That is, relative marginal productivities change over time, causing variations in relative returns. Second, when the restriction implied by (16) is imposed we are testing the hypothesis that the rate of growth of g(.) is linear, i.e. that this progress increases the productivity of one type of labor more than the other’s in a constant fashion overtime, which is fully compatible with the evidence found when analyzing demand shifts. For our technological inquiry, we follow MRR’s procedure almost exactly, while for the trade part of the analysis we devise new ways to estimate (16). For now, we turn our attention to the technology aspect. 16 To estimate (16) the fixed weight log earnings differential between highly and low educated workers is used as the dependent variable. We define the highly educated workers as those individuals who have a college degree or more. Unskilled workers are those having between 6 and 11 completed years13. We chose these groups for two reasons. First, we saw above that the growth in earnings of highly educated individuals cannot be explained by shifts in net supply alone, so our objective is to examine in more detail their earnings. Second, this framework is especially useful for examining relative earnings, and high school workers are a good comparison group due to its relative size and earnings beahvior. The data come from of a series of urban ENHs covering 22 years between 1977 and 1998 mainly for the month of September. We use the same criteria above to drop observations, divide the sample into skill groups, and to compute fixed weight earnings for aggregated groups. The results from estimating (16) are (small numbers below the coefficients are standard errors) W H ln H (t ) = 0.01 + 0.029 t − 0.476 ln 0.007 0.201 L WL (16a) Predicted and actual values are plotted in Figure 4.5. By inspecting Figure 4.5 we can see that equation (16) does a good job of explaining the variation of the earnings differential between college and high school workers, except for the periods 1979-82, 88-90 and the very last year (1997-98). We have found important evidence telling us that changes in relative supplies combined to constant growth in productivity differentials between these two groups are able to explain the rise in relative earnings for most of the period under study. Figure 4.5a shows the trend of the relative earnings series against the observed differentials. Two things are apparent. First, the periods that require more attention are 1979-82 and 1991-93, when the actual differential deviated from the trend downwards and upwards, respectively. Second, from 1983 to 1990 the slopes of these curves are very close. Even for the years 1993-98 if we plot a 3-year moving average of the differential against the trend, the slopes are surprisingly similar. These facts call for a closer examination of the time path of g(t). Note that (15) implies that g(t)= gA(t)- gB(t) is equal to g (t ) = 1 WH Ln γ WL H + (γ − 1) Ln − a L (17) The results given in expression (16a) imply a value for the elasticity of substitution between college and high school workers of 1.476, which we use to compute the implied time path of g(t) according to equation (17), along with hypothetical values for that elasticity of 1.3, 1.65 and 3. In Figure 4.5b we plot these paths accompanied by trend lines coming from regressions of each g(t) on time. For all values of the elasticity the slopes of the actual g(.) and the trend are very close. 13 We do not follow the aggregation scheme used by MRR to differentiate H and L. See their paper. 17 Also, the implied paths of g(t) fit a straight line almost perfectly, which constitutes one of the main results extracted from this exercise, because it provides evidence pointing to the existence of a technological process that is augmenting the productivity of college labor more rapidly than that of high school individuals, and that this increase in the differential is well captured by a linear growth over the last 22 years, with small deviation from the trend from time to time. The computed trends imply a yearly simple average growth of g(t) of about 2%. The second piece of evidence that we extract from the figure is that there seems to be a period of decrease in the rate of growth of g(t) from about 1984 to 1987/88, followed by catching up to trend level and then a new short period of slowdown between 1989-91. The intervals in which g(t) grows faster than the trend are 1978-80, 1992-94 and the last two years14. Note the similarity of these results and those of MRR for the US over the years 1960-1995. They found an elasticity of 1.42. Taking into account that the vast majority of Colombia’s external trade takes place with the US, that foreign investment comes mainly from the US, and that the dollar is the dominant currency for foreign exchange policy, this may tell us that both countries have been subject to similar technical change and trade shocks. We finish the technology part of the analysis by inspecting Figure 4.5c, in which we depict actual and detrended changes in relative supplies of college versus high school workers. This variable has grown at an average rate of about 3.8% per year over the entire period. The relative supply of college individuals grew faster than average only during the periods 1978-79 and 1996-98. For the years 1989-95 the rise in this aggregate was substantially below average, while the interval 1980-88 was characterized by a small downward deviation form the average pattern. These facts, combined with the evidence found before regarding the behavior over time of the function g(t) provide a compact explanation of the behavior of the college-high school earnings differential. That is, if we turn back our attention to Figure 4.5, we notice that by estimating equation (16) we are under-predicting the growth of the differential during 1979-80 and 1991-1993, which are precisely the periods for which we observe the function g(t) growing faster, combined with the relative supplies growing slower than average. The period 1982-1988, when the changes in the differential are perfectly predicted, corresponds to an interval of close-to-average movements in both g(t) and relative supply. Therefore, we can conclude that changes in relative supplies combined with an almost constant rate of increase in the skill bias of technology towards highly educated workers fit data well, and this allows us to explain the rise in relative earnings of that group of workers. As MRR and KM note for the US, this can be also interpreted as technological change increasing demand disproportionately for more educated workers in a constant fashion over time. The results found here are fully compatible with the ones of the previous section regarding relative shifts in demand (especially the “within” component) and the inability of a simple supply-demand framework to explain the increase in college workers’ earnings. 14 We carried out a statistical test for changes in the growth rate of g (see MRR’s paper, pp 30-31 for the exact specification of the test) It yielded significant changes for the growth rate in the years 1981, 92, 94 and 98. For 1981 and 94 the sign indicates downward deviations from the trend, while the opposite is true for the other two periods. Thus, we conclude that the rate of growth of g(t) slowed down during the 80s, accelerated between 1992-94 and then decayed in the latter part of the 90s until 1998, when it sped up. 18 Labor demand shifts induced by external trade flows also contributed, but to a lesser extent. The trade part of the exercise is very simple. It consists of computing the supplies of college and high school workers implicit in trade flows according to equation (11), and then adding these implicit supplies to the actual supply series. We then calculate new relative quantity series and re-estimate equation (16) to assess the effect of trade flows on changes in relative earnings from the perspective of factor content theory. We start by analyzing Table 4.8 where we summarize the changes in total and relative supplies induced by trade flows. In the first column we find the adjusted total supply of workers with the domestic labor force normalized to one. Two comments are in order. First, the effects of the opening of the economy can be detected only starting in 1993 when the adjusted supply went from 1.086 in 1992 to 1.132, and reached a maximum value of 1.167 in 1995. In the last part of the decade it stabilized around 1.13. Second, from the point of view of labor quantities this liberalizing event has not been as important as believed. In fact, the opening that occurred at the beginning of the 80s (1980-84), which is regarded in Colombia as a very modest liberalization of import restrictions, appears to be more important quantitatively because during those years the measure of total labor supply was consistently around 1.15. The second and third columns of the Table show that the effect of trade flows on the relative supply of college vs. high school workers has been very modest, although there is a change in the pattern starting in 1992. The changes seem too small to explain any significant part of the changes in relative earnings. The results of estimating equation (16) with the adjusted supply series are the following W H ln H (t ) = −0.072 + 0.028 t − 0.527 ln 0.007 0.217 L WL (16b) Instead of analyzing the effect of trade by means of a graph comparing the time path of the two series of predicted values, we present them in Table 4.9 along with the percentage changes in the college-high school earnings differential. There we can see how the adjusted supply series moves the predicted values closer to the actual earnings differentials, especially for the period 19911993. The accumulated growth in the actual differential during this two-year period was 24.9%, while equation (16) estimated with the unadjusted supply series predicted an increase of 7.6%. If we instead estimate (16) with the adjusted series the predicted rise of the differential is of 9%, which leads us to conclude that the growth of net imports is responsible for approximately 5.6% of the increase in the college-high school differential (5.6=(9-7.6)/24.9), figure which is in line with the conservative estimates made for the US (see for example Borjas, Freeman and Katz, 1992 and 1998). In conclusion, in this section we used a simple framework to account for the growth of relative earnings of the college educated, based on factor biased technological change, relative supply measures and external trade. The contribution of this last factor was very modest. Our last task is to provide at least a partial explanation of the rise in female earnings. Gender: I argue that the bulk of the gains experienced by women are due to a reduction in pure labor market discrimination. We found above that relative demand shifts coming both from changes in the industrial composition of the economy, and from external trade flows display the right signs, but once female supply is taken into account these are not enough to explain the observed changes in the male-female earnings differential. Technical change cannot be considered as a main factor to explain such changes due to the evidence offered by the within component of demand shifts examined above. Thus, I estimate a simple reduced form equation to 19 test the hypothesis of reduction in discrimination as follows: y i = β i xi + ε i for i = male(m), female( f ) (19) where y is the log earnings, x is a matrix of personal characteristics including education, experience, hours worked, sectoral affiliation, dummies for age groups and city of residence and profession (the “endowments”), and β is a vector of parameters that measures the “prices” paid for those endowments to men and women. After estimating (19) for both genders separately, I proceed to predict two wages for women according to the following equations yˆ f = βˆ f x f , yˆ m f = βˆ m x f (19a, 19b) The first of these quantities (yf) simply measures the earnings for women as if the variables included in x were able to account for the entire variation of female earnings, while the second (ymf) constitutes a counterfactual wage measure for women, displaying how much they would earn if they were paid at men’s prices. The difference between these two quantities can be interpreted as discrimination in the sense that for the same observables we detect different prices that depend solely on the sex of the worker. However, a word of caution is in order. Since the measure of experience used here is potential and not actual, and taking into account that actual experience is lower among women than men, the difference between these two measures may be picking some of this effect as well. There may also be unobservable differences between male and female labor that play a role in the disparity. Figure 5.6 depicts the difference between these two predicted earnings values along the female’s earnings support, partitioned into 5% percentiles for ease of presentation for three years of the data (1978, 91 and 1998). We can see that the discrimination component, as defined here, decayed all along the earnings range, but the fall was especially sharp within the first 50%. The “discrimination profile” went from having a steep negative slope along the initial 50%, to a practically flat line around 0.25 log points. This exercise concludes the urban part of the analysis. Now we switch our attention to the rural sector, which will be analyzed in a briefer manner than the urban for a number of reasons, such as the lack of information to carry out many of the exercises, but more importantly because the already mentioned fact that the relationship among skill and earnings is not as strong in rural areas. Also, as we saw in the descriptive section the changes in the distribution that occurred in the period 1988-98 were not of great magnitude and did not show identifiable patterns. We start by estimating equation (9) for the 24 skill groups defined for the rural sample only for the first two demand shift indices as explained in the urban section. The results are presented in Table 4.10. As expected, the Table shows that supply and demand for the various levels of skill do not by themselves account for earnings changes. Surprisingly, however, the only periods in which the model displays at least moderate explaining power are 1991-94 and 94-96, which cover the opening up of the economy, and this result is particularly strong for the first interval. As we can see in the Table, the values obtained for the elasticity of substitution fall within the correct 20 range, and are significant. Now we implement equation (3) of KM’s paper, which will help us in cleaning the data from cell specific trends related to technical progress, which may have played a very important role, especially during the 80s. This exercise simply consists of computing the inner product of the vector of earning changes times the vector of net supplies changes, measured in efficiency units (see also footnote 9 in their paper for a detailed and formal explanation of the procedure). We can see the figures obtained from this exercise in Table 4.10a. They show that once cell specific trends are partially removed, the periods for which changes in wages may be adequately explained by supply and demand interaction are 1978-88 and 1991-94. This finding is important for two reasons. First, the 1980s were a period of rapid modernization for the Colombian agricultural sector (see for example Bejarano, 1992), and in 1986 a medium sized coffee boom occurred. Thus, once we remove these effects from the price-quantity measures we see that that earnings moved according to shifts in net demand for the various levels of skill. Second, the fact that movements in relative earnings can be explained by such shifts during the first half of the 90s, is evidence against the popular view that the deterioration of labor earnings in rural areas was due to the increase in net trade flows. Finally, the results obtained for the second half of the 1990s are consistent with the increase in violence coming from various sources, falling international prices for exports and the recession. Table 4.11 replicates Table 4.5 for the rural case. We compute the demand shift index with j indexing only the 33 industrial sectors, because the occupational distribution has remained practically unchanged, with almost 80% of the sample being either a family worker or selfemployed. The negative correlation between net supply and wage changes is almost non-existent except for the period 1991-94 and, surprisingly, for the entire period. Over this period the supply of men decreased by 5%, while women’s increased by almost 25%, but this rise occurred entirely between 1978-91. Indeed, in the 90s female labor supply fell by 15 percentage points. Demand for female labor displayed the same qualitative behavior but showed smaller changes, while demand for male labor did not change neither during the entire period nor within individual intervals. As a result, supply of female labor increased by 14%, and male’s fell by 6%. Women’s fixed weight earnings rose despite the increase in net supply (by about 25%). There has been a move toward a more educated rural labor force. Uneducated workers reduced their share by more than 35%, while the highly educated increased theirs by 185%. High school individuals’ supply grew by more than 80% and primary ones kept their share constant. The majority of these changes occurred in the initial period and between 1994 and 1996 the shifts go in the opposite direction from the pattern observed in other periods. Demand growth was close to zero in the aggregate. The college group experienced a rise in demand for its services of about 70%, but during the 90s demand for college-educated workers fell more than 90%. The two lower categories experienced stable demand within every sub-period, while the high school workers experienced demand shifts that were qualitatively similar to those for college workers. The supplies of the two higher groups increased dramatically (75 and 135%), while earnings decreased for the high school group and increased for college educated workers. Earnings for uneducated and high school workers thus seem to be adequately explained by supply and demand movements over the entire period. The supply of educated women grows more than men’s, the reduction of the share of uneducated female labor is also greater, and changes in wages are larger as well. Hence, we have again two unexplained wage changes: college individuals, whose earnings move almost randomly, and women. We looked for evidence of shifts in participation 21 rates, occupation and sector, among other things, seeking some explanation. Instead, what I found was that in 1991 there were a few educated earners who made unusually high amounts of money. Demand Shifts Coming from International Trade Flows: Table 4.12 presents the aggregated supply of workers of different skill levels implicit in trade flows, as measured by equation (11). In contrast to the urban sector, the rural one has been a net exporter of workers of every skill category, except college educated men, which in principle constitutes an additional fact that goes in the opposite direction of what we expected given the rise of these workers’ earnings. The qualification “in principle” means that the relative demand shifts that will be presented shortly constitute more reliable measures than this raw supply index. In the aggregate and for every subgroup, the implicit supply of workers increased over time (i.e. it became less negative), except for the latest period analyzed when it went down. Demand shift indices for the more aggregated groups are presented in Table 4.12a. Two facts are immediately apparent. First, external trade has had a negligible positive impact on demand for male workers, while its effect on female’s has been negative and quantitatively more important than the one observed for men. Second, across educational categories trade has reduced demand for college educated individuals and increased that for uneducated workers. Demand for high school individuals has also been reduced and primary’s has not been affected importantly. Therefore, (i) import competing sectors in rural areas are low skill when compared to export ones (the opposite situation to the one detected in urban areas), and (ii) movements in labor quantities arising from trade flows were not consistent with wage changes for college workers (except between 1991-94), while the opposite is true for uneducated and high school workers. Thus, we conclude from a pure demand-supply perspective that if trade had any effect on labor earnings of this group, it was to partially counteract the increasing pattern caused by other factors15. DECOMPOSITION OF CHANGES IN THE DISTRIBUTION OF INCOME In the previous section we related the changes in the distribution of labor income in Colombia during the last 20 years to the skill composition of the labor force. In doing this, we sought to explain changes in the rewards to different skills in a supply-demand framework. In this section we carry out a complementary exercise in which we isolate and quantify the contribution of single factors to changes in the distribution of labor income over time, holding other variables constant. That is, we construct counterfactual distributions to answer questions such as “how would the distribution of income have looked at time t had some factor x remained at its t-1 level, and workers had been paid according to the time t earnings schedule?”. This exercise uses the methodology proposed by DiNardo, Fortin and Lemieux (1996, DFL hereafter), which is in the spirit of more traditional methods that decompose changes in the moments of random variables. Examples of such procedures include the Oaxaca methodology that quantifies the contributions 15 Since the growth of women’s labor earnings remains unaccounted for, we carried the same exercise undertaken for the urban sector. The results show that there has not been a reduction in the discrimination component of the rural earnings schedule. In fact, women belonging to the initial 50% of the income range were subject to more discrimination in 1998 than in 1978, while those along the 50th and 70th percentiles were about in the same situation. Thus, we close the rural section noting that the earnings gains experienced by women in rural areas are not accounted for in this analysis. 22 of individual variables to differences in means (Oaxaca, 1973), and variance decompositions. The DFL procedure generalizes these methodologies by decomposing changes in the entire distribution. This is done by nonparametrically estimating the density function, and then reweighting it to produce a counterfactual density. This reweighting adjusts the time t density for the change in probabilities between the two dates of observing one particular characteristic for each observation in the sample. We start with the weighted kernel estimate of the density function of income Y: 1 n Y − y fˆ ( y ) = wi K i ∑ nh i =1 h (20) The variables h and n are the bandwidth and the number of observations, and wi is the (re)weighting function, which is the product of two elements ui and Ri. The first of these is just the sampling weight, but the second is the key to the procedure. Suppose income and personal characteristics (including education, gender, experience, marital status, city of residence, profession and trade) have a joint probability distribution at some point in time. Each individual can be regarded as a vector x=(y, z) consisting of income and another vector z of personal characteristics, indexed by time. Partition z into two components, r and v, where r is any individual element of z that is of special interest, and v is the rest of the elements of z. We want to decompose the change in f(.) between two dates t=1 and t=2, in which the actual densities are given by (20) with Ri=1 for all i. Since f ( y, x) = f ( y | x) f ( x ) , we can express the actual density at time 2 as: f ( y | t y = 2, t r|v = 2, t v = 2) = ∫∫ f ( y | r , v, t y = 2) f (r | v, t r |v = 2) f (v | t v = 2)drdv (21)16 The l.h.s summarizes DFL’s notation that for the most part will be used here as well. It tells us that the observed density in time 2 depends on the income schedule at that time (ty), the distribution of the attribute r given the particular realizations of the other attributes contained in z (tr|v), and finally on the distribution of the latter (tv). We seek the distribution that would have been observed at time 2 if the distribution of r given v had remained as it was in t=1 and people were paid as they were in t=2. Hence, we are looking for f ( y | t y = 2, t r|v = 1, t v = 2) . From (21) we have f ( y | t y = 2, t r |v = 1, t v = 2) = ∫ ∫ f ( y | r , v, t y = 2) f (r | v, t v = 1) f (v | t v = 2)drdv = = ∫ ∫ f ( y | r , v, t y = 2) Rr|v (r , v) f (r | v, t r |v = 2) f (v | t v = 2)drdv (21a) for Rr|v (r , v ) = f (r | v, t r|v = 1) f (r | v, t r|v = 2) 16 (22) Note that this notation implicitly assumes continuous random variables. 23 The lower part of the r.h.s of equation (21a) is identical to the r.h.s of (21), except for the R(.) function. If we can estimate (22), then we can compute the counterfactual density for characteristic r. The function defined in (22) measures the ratio of the probabilities of observing r, given the realizations of v at dates t=1 and t=2. Therefore, if r is a dichotomous variable R r |v ( r , v ) = r Pr(r = 1 | v, t r|v = 1) Pr(r = 1 | v, t r|v = 2) + (1 − r ) Pr(r = 0 | v, t r|v = 1) (22a) Pr(r = 0 | v, t r |v = 2) Equation (22a) is the relationship that we use to measure the contribution of attribute r to the observed change in the densities. Once the first counterfactual density is constructed, we can pick other elements of v and carry out sequential decompositions. Once this sequential exercise is over, we want to measure the effect of the remaining elements of v as whole. That is, we seek the density f ( y | t y = 2, t r|v = 1, t v = 1) . Applying the same logic, f ( y | t y = 2, t r |v = 1, t v = 1) = ∫ ∫ f ( y | r , v, t y = 2) f (r | v, t v = 1) f (v | t v = 1)drdv = = ∫ ∫ f ( y | r , v, t y = 2) Rr|v f (r | v, t r|v = 2) Rv f (v | t v = 2)drdv for Rv (v) = f (v | t v = 1) f (v | t v = 2) (23) Applying Bayes’ rule to (23) we get Rv (v ) = f (t v = 1 | v) Pr(t v = 2) , f (t v = 2 | v ) Pr(t v = 1) (23a) which simply measures the weighted probability of an observation falling in year 1 or in year 2 given the characteristics of the workers. The weight is the ratio of unconditional probabilities of an observation belonging to either date. The final step of the decomposition exercise accounts for the effect that supply and demand factors had in the evolution of labor income inequality. Following DFL, the procedure used to compute the supply-demand counterfactual density is to estimate the earnings shift for each skill group according to equation (9), subtract this quantity from the actual earnings in time 2, and then estimate the density of these hypothetical earnings. We estimate (9) in second differences to eliminate cell-specific effects. Also, two modifications are introduced to (9): first, we allow for a constant term and second, we do not restrict the changes in supply and demand to have equal coefficient in absolute value. Thus, the supplydemand counterfactual once we have controlled for individual attributes is given by f ( y | t y = 2, t r |v = 1, t v = 1, s = 1, d = 1) = f ( y − ∆y | t y = 2, t r|v = 1, t v = 1) (24) where ∆y stands for the estimated shift in earnings for each cell (dropping the subscript to save on notation). We finish this methodological section by listing the elements of z and by briefly explaining the estimation procedure of (23a). The vector z consists of years of education, experience, gender, occupation, city of residence, number of years there, marital status, profession, hours worked, trade, and type of job (temporary/permanent). Expression (23a) measures the probability of being in the sample in years 1 or 2, given the distribution of personal 24 characteristics. To estimate Rv(r,v) we fit a logit model with the date as the dependent variable and a vector with the elements of v as the independent variable, and then compute the appropriate fraction. The ratio of unconditional probabilities is calculated by dividing the number of observations in period 2 by that of period 1 (adjusted by the sampling weights). Finally, the data set used for the labor earnings decompositions is equal to the one used in the previous section17. Results: The objective of the first decomposition is to isolate the contribution of trade flows to the changes in the distribution of earnings. We assume that the distribution of workers across the various net import penetration levels, as defined in the methodological section, is a random variable that covaries with labor income. We are not implying any causality between these variables, the only implication of the exercise is the assumption stated above. The import coefficient was turned into a dichotomous variable taking on the values 1 if the individual worked in a sector in which the net import coefficient was greater or equal than 0.1 and 0 otherwise. Then we fitted a logit equation of this variable on dummies for the 48 skill groups, years of education and experience within these groups, a quartic in experience, occupation, type of job, city and years of residence, hours worked and profession. This estimation gives us the probability for each observation of belonging to a high importing sector in date 1, given its individual characteristics. With these probabilities we constructed the reweighting function Rr|v (r , v) to estimate the trade counterfactual density for date 2. With the same covariates we estimated the probability of being in either date 1 or 2 and computed the function Rv (.) as explained above, and the reweighting function R(.) = Rr|v Rv was computed. Finally, the supply and demand counterfactual was computed according to the procedure explained before. We undertook decompositions for the 15 possible combinations of the 6 years of the data, but report results only for 1988-94, 94-96 and 96-98.The first of these intervals spans the trade reform. Figures 4.7 through 4.7b show the results of the exercise for these periods. Graphs are read as follows: in the first panel we plot the two actual densities for dates 1 and 2. The second shows the actual density for date 2 and the trade counterfactual, while the third displays the trade counterfactual density and the personal attributes one. The fourth panel shows the personal attributes counterfactual and the supply-demand hypothetical density, and the last panel depicts this last density and the actual one for date 1, i.e. the residual or unexplained change. Thus, if the elements of z=(r,v) were able to account for the entire change, this last panel would show two identical functions. Finally, vertical lines are drawn at the 5th, 25th, 50th, 75th and 95th percentiles of the actual distribution for date 1 to better interpret the changes. Figure 4.7 plots the decomposition of the change in the density of labor income from 1988 to 1994. The figure shows that the changes induced by the increased level of net imports were concentrated in the left and right tails of the density, and along 50-90th percentiles of the original distribution. The increase in net imports reduced the probability mass at the very left of the support and increased it at the opposite end. Additionally, the mass located above the median and below the 75th percentile grew, while that along 75-95% of the earnings range was reduced. This suggests that higher levels of net imports made the distribution more equal, not less so as it is 17 The labor earnings DFL decomposition is carried out only for urban areas. 25 widely believed. These changes are consistent with the demand shifts induced by trade studied in the previous section. In particular, demand for less skilled workers grew relative to that for more skilled individuals as imports increased, while the demand shifts induced by this variable were unfavorable to workers with intermediate levels of ability. Regarding the remaining attributes of the workers, the graph shows that the contributions made by these during this period were negligible. Supply and demand interaction, on the other hand, reduced the probability mass in the very left, and also in the middle-high sections of the distribution, while increasing it substantially between the 5th and 25th percentiles of the 1988 distribution, and also along 75th-95th percentiles. Hence, supply and demand factors probably worsened the overall distribution in this period. The period 1994-96 is shown in Figure 4.7a. Trade had similar effects to those observed over 1988-94. The contribution of supply and demand factors was practically zero over this period. The only noticeable effect of these factors was a minimal increase in the mass located at the very left of the income range, accompanied by an equally small reduction at the opposite side. This confirms the results found in the previous section that pointed to the neutrality of supply and demand for skill in the wage formation process during this period. The final two-year interval is shown in Figure 4.7b. During these years (1996-98) the contributions made by trade and personal characteristics were very small. The next to last panel of the Figure plots the supply and demand counterfactual, in which we notice that these factors had unequalizing effects. More particularly, they increased the mass along the 25-75th percentiles, and at the top 5% of the income range. The decomposition exercise carried out for the period 1978-88 is not shown. However, over this period changes in personal attributes account for most of the change in the densities, due to the fact that changes in their distribution were very large. After 1988, changes in the distribution of personal characteristics have less influence, although their shifts were still important, especially for the occupation variable. Developments of the main covariates are presented in Table 4.13. In summary, for the first period analyzed the covariates account for most of the observed change, while the opposite is true for the latter two intervals. The increased level of net imports of the 1990s reduced inequality, because it favored the poorest segments of the distribution, whereas supply and demand factors generally increased inequality. These findings (and the evolution of occupation in the earlier periods) prompted us to carry out more detailed decompositions that would be able to account for a larger share of the changes. We performed several robustness for the exercise just discussed. The first consisted of inverting the order of the decomposition. That is, we started with supply and demand, continued with personal attributes excluding trade, and finished with the latter. Since the personal attributes counterfactual density is now constructed before having controlled for trade, while the trade counterfactual is estimated unconditionally, we need to compute two new reweighting functions, Rv|r and Rr. This computations are straightforward by noticing that f(X|Y)f(Y)=f(Y|X)f(X) and thus R v| r ( r , v ) = Rr |v (r , v) Rv (v ) Rr ( r ) , Rr ( r ) = Pr(t r = 1 | r ) Pr(t r = 2) Pr(t r = 2 | r ) Pr(t r = 1) Since the trade variable was turned into a dichotomous one, the function Rr, is a simple ratio of individuals employed in high importing sectors, to those working in low importing ones. The results were robust to the order of the decomposition, noting that the contributions made by 26 supply-demand and trade were slightly lower in every period (especially 1988-94) when the reverse order was applied. This shows that when we remove changes attributable to personal characteristics and trade, the effects of supply and demand are magnified because we allow the counterfactual to pick up just the effects of those variables. That is, when supply and demand are analyzed first, their action may be confounded with that of other attributes, especially education, gender and experience. The slight reduction of the contribution of trade shows one point that has been mentioned already, which is that it is very likely that trade and supply and demand for skill interact in some way, especially in 1988-94. The second set of checks is related to the variables included in v, which were changed and combined in several different ways. Next, we tried various alternative estimation methodologies for the reweighting functions. For example, we estimated the probability of an observation falling in a high importing sector by fitting a logit equation, a probit one and nonparametrically. The latter means that I divided the sample in very fine cells according the elements of v, and computed the proportion of high importing observations in each cell at time 1, and then used this proportion to compute Rr|v. All the decompositions were quite robust to the choice of covariates or the estimation methodology, excepting most of the exercises involving the year 1978. Additionally, the exercises for this year produced very jagged densities, and for these two reasons they are not shown. Finally, I carried out the main exercise for hourly wages, obtaining exactly the same results. The results discussed above suggest a role for the recession that started in 1996, because the decomposition showed that personal attributes and supply-demand for different skill levels were not able to account for most of the changes in the distribution of earnings. That is, the increase in inequality may be partially explained by factors that lie outside the labor market. The presence of factor biased technical change favoring the more skilled was shown in the previous section to be the main factor lying behind their relative earnings performance, which combined to macroeconomic shocks that affect the earnings and employment of the poorer groups may be responsible for the increase in inequality. We sought for a decomposition exercise that would be able to partially capture these effects. Also, we wanted to extract more r variables from v to check if the lack of explanatory power of personal attributes is the result of aggregating the effect of several characteristics into one overall function. Maybe some of the elements of v taken individually interact with the outside shocks in different ways and explain a larger share of the change in inequality (for example, education may play an important role due to its power to isolate the highly educated from the effects of macroeconomic shocks). Therefore, our next exercise consists of a more detailed sequential decomposition with employment as the first step, proxying the macroeconomic shocks. We do this by incorporating in the sample all active workers to compute the probability of being employed at date 1, given the other personal attributes for each observation. This quantity is then used to calculate the function Rr|v according to equation (22a). Next, we sequentially extract elements from v and compute reweighting functions based on the probabilities of these variables taking on one particular value at date 1. The r variables chosen are, after employment, trade (same definition as before), education (11 or more years=1), occupation (self-employed=1) and gender. Then, with the remaining elements of v we calculate the personal attributes counterfactual in the same way as above. Finally, the supply and demand counterfactual is computed. In this exercise we are assuming that wages and employment have a joint probability distribution. Under this assumption we view unemployment as excess supply of workers that tends to drive earnings down. The procedure is related to the Heckman two stage method (Heckman, 1976, 79). 27 The results from this exercise are presented quantitatively rather than graphically. From the various estimated densities we computed the Gini coefficient (g) and several log percentile differentials. In this way we quantify the contribution of each factor in isolation, and we keep the nonparametric nature of the procedure The computation of various differentials allows us to study the effects of each variable on different segments of the distribution. The differentials used are the 90th-10th and 75th-25th. Since once we carry the decomposition we have the density values for each point on the earnings support, it is straightforward to compute those quantities as ∞ g = 1 − 2 ∫ F1 ( y ) f ( y )dy where F1 ( x) = 0 x 1 yf ( y )dy and µ is the mean wage. µ ∫0 The qth percentile of the distribution is given by the value of w for which the following is true w q = ∫ f ( y )dy 0 The results of this exercise are presented in Table 4.14 for the same three periods analyzed before, and using the same format used when we presented the results graphically. Each cell contains the change in the relevant measure of inequality between the two densities involved. Below this number the percentage contribution of the factor to the overall change can be found. The last column adds up the individual contributions. Inequality rose along every segment of the distribution over 1988-94, especially for the 75th-25th differential. The decomposition exercise explains 89, 128 and 71% of the change in the Gini, and the 90th-10th and 75th-25th differentials, respectively. The factors that made positive contributions to the increase in inequality were education, occupation and supply and demand. Employment and trade worked to reduce earnings dispersion. The equalizing effect of employment was especially large for the tails of the distribution, resulting from the fact that during this period the uneducated were the only ones who endured growing unemployment. Trade flows had a strong equalizing effect involving also the top and bottom 10% of the distribution, while they slightly increased inequality between the lowest and highest quartiles. As a result, their contribution to the change of the Gini coefficient was equalizing but small (this index is more sensible to changes in the center of the distribution). Education was the strongest unequalizing factor everywhere in the distribution, finding that accords with the results of Vélez, Bouillon and Kugler (1999) and Sánchez and Núñez (1998, 1998a). As strange as it may seem, this result arises because the educational earnings differential grew in favor of college individuals, at the same time that the supply of high school educated workers kept growing. This behavior could be summarized as the country having too many high school educated individuals. Occupation during this period was associated to a rise in inequality concentrated in the tails, pointing again to a shift of the highly educated and female labor towards highly paid occupations, such as white collar, and away from low paid ones such as domestic service. However, occupation reduced the 25th-75th differential, which is again related to the shifts observed in the female occupational distribution shown in Table 4.13 and analyzed before. Regarding the gender variable, the shift to a larger share of female labor contributed to reduce inequality. The remaining personal attributes (city and years of residence, sector of employment, experience, type of work and profession) significantly reduced 28 the 90-10th differential. We ran regressions of the log of income on these variables and human capital ones for both years and interpreted the parameters of the sectoral and city dummies as the respective premia paid by each sector and city. The regional variable did not play an important role. Changes in sectoral premia are shown in Table 4.13 compared to retail commerce, which is the most numerous sector. We see that all premia but three were reduced during this period. Additionally, note that the sectors that display the highest premia happen to be either the most protected or non-tradable, and all of them reduced this premia after the opening of the economy. This is an additional channel through which trade contributed to reduce earnings inequality. Finally, the interaction of supply and demand for skills had unequalizing effects on earnings, which were magnified for the measures that included the highest ability. In the next period (1994-96), Table 4.14 shows that the decomposition exercise predicts increases in inequality, irrespective of the measure used. However, the data displays the Gini coefficient and 75th-25th differential decaying and the 90th-10th growing significantly. Occupation and supplydemand did not play any role in this period, while employment, trade and gender contributed to inequality reduction. Education and personal attributes contributed to increase inequality. The effect of personal characteristics was particularly strong in the tails, while that of education was concentrated in the 75th-25th differential, but the equalizing effect of employment and gender was large for this differential as well, offsetting the education effect. The fact that personal characteristics acted in the direction of increasing inequality is an indirect reflection of the downturn of the economic cycle, because the evolution of the different covariates presented in Table 4.13 shows very modest developments and in the direction of reducing dispersion. The final period (1996-98) is one of increasing inequality for all measures. The decomposition picks up this pattern correctly, and over explains the increase of the Gini and of the 75th-25th differential, while it accounts for more than 81% of the rise of the 90th-10th differential. The equalizing effect of employment and trade is weaker, which results from unemployment increasing more in this period for the highly educated segment than over any other interval. Also, employment for the least educated increased. Regarding trade, net imports went down between these two years. The unequalizing effect of education was weaker as well, reflecting the increase in the growth rate of the supply of college individuals. Occupation again displayed unequalizing effects, except for the 75th-25th differential, probably reflecting the increased share of selfemployment. Personal attributes and supply-demand had negligible effects. In summary, the effect of the employment on inequality was always equalizing. Although this may seem at first a trivial result, it goes to the bottom of the problem: demand for labor in urban Colombia is becoming everyday more skill oriented, even during 1988-94 when the overall unemployment rate fell from 9.8 to 7.4%. Although the supply of highly educated workers is growing, except in the period 1996-98, it is doing so at a very slow rate. At the same time, the supply of intermediate education keeps growing at a very fast pace. Second, it is clear that trade did not have the adverse effects on the distribution of labor income that it is associated with. This finding is consistent with the way imports increase demand for uneducated workers, while reducing it for high school workers. This equalizing effect also is related to the fact that they favor female labor demand. The methodology used in this section is different from the one used in the previous section, and they yielded identical results pointing to trade lowering inequality. However, trade may have other effects ignored here, among which we mention input-output effects and an interaction with technical change (although this is partially captured by the 29 decomposition). We saw that the latter seemed to have sped up around the same time in which the reform took place (1992/93), indicating a possible relationship between the two. Finally, the evidence regarding occupation gives additional support to the technical progress hypothesis18. We finish with an additional exercise intended mainly for testing the presence of factor biased technical change. We run weighted regressions of the log of income on human capital variables plus city of residence and hours worked for each of the four years used (1988, 94, 96 and 98). The weights are given by the different R(.) functions times the sampling weights. Then we predict earnings and residuals for each year. Thus, this exercise permits us to study the effect of each covariate on the evolution of observed inequality (measured by the standard deviation of predicted log wages), and unobserved dispersion (standard deviation of log residuals), which may be thought of as measuring the “between” and “within” components of inequality. Additionally, the second component is a good indicator of the presence of unobservable forces that affect earnings, such as technical change. These quantities are presented in Table 4.15 in the same format of Table 4.14. The first important point is that over the earliest and latest time intervals both observable and residual inequality increased, while during 1994-96 the rise only occurred in observable inequality. In the section in which we analyzed technical change in detail we found that this process slowed down around 1994/95, after having sped up two years before. The fact that residual inequality decreased between 1994 and 96 is completely consistent with this finding. More importantly, the Table shows that the decomposition exercise lacks any explaining power for the residual component of inequality, except in the period 1994-96. Thus, only during this period the variables used in the decomposition, which comprise practically all measurable factors, are able to account for the changes in this component. In the remaining periods some other factor is driving it. The second point is related to employment. The Table shows that the equalizing effect of this variable during the period 1988-96 was restricted to the residual component, meaning that observed inequality increased as a result of shifts in employment. Therefore, in the latest period the way in which this variable influenced the distribution of earnings changed as a result of the huge rise in the unemployment rate, especially among high school and primary workers. Additionally, in the earlier periods (1988-96) employment contributed to increase educational differentials. The next point has to do with trade and its relation with educational differentials. As we discovered in the technology/education exercise, trade contributed to the increase of the college-high school differential. In this decomposition exercise we find additional proof of that fact. We see that trade accounts for 44 and 59% of the increase of the college/rest differential. This figure is higher than the one found above, which leads me to conclude that trade may be responsible for 30-40% of the increase in educational premia during the first half of the 1990s. If we analyze the education variable we see that, as a rule, the shifts of this variable increased measured inequality and reduced unexplained dispersion. This point is another way to see that the increases in the relative supply of college educated individuals is less than the one needed. Finally, supply and demand factors are an important explaining factor for the observable 18 Again, we carried out several robustness checks. They were to change the order of the decomposition between the r variables and to use alternative estimation methodologies for the different probabilities. The results were robust, excepting again the decompositions involving 1978, and in some instances the results regarding occupation in the period 1994-96 were not very robust. Also, we repeated the 1998-94 period using hourly wages with no change in the conclusions. 30 component of inequality (especially in 1988-94), which is consistent with the results found all along the paper. CONCLUSION This paper starts by investigating the evolution of the distribution of labor earnings from a skill perspective. We confront the problem from two perspectives. First, using a simple supplydemand framework for different skills to evaluate the role these played, and how they affected the distribution of labor earnings at different points in time. Skill is proxied by education, experience and gender. Second, we relate income to several demographical, skill and labor market factors, to quantify their effect on the evolution of that distribution along the entire income range, and on other measures of dispersion and on skill differentials. This approach is a semi-parametric technique to decompose changes in density functions over time. In urban areas, we found a reduction in the differential between the least educated and the college educated workers, an improvement of the relative position of younger entrants to the market, and earnings gains for women. On the other hand, we found a worsening of the position of intermediately educated individuals, and relative income gains for the more experienced workers during the 1990s. Over time, 1978-88 was a period of reduced inequality between groups, while after 1988 the opposite happened due to the rise in earnings of the highly educated, and of the more experienced workers among the highly educated. In rural areas, the main conclusion was that the increase in inequality was not linked to rising prices of higher skill levels. The microeconomic model used provided a compact explanation for most of the changes in urban areas, excepting the rise in earnings of female workers. More particularly, it was shown that the interaction of supply and demand for skill fully explained the behavior of earnings for all educational groups, but the college one. The secular worsening of the relative position of the intermediate group (high school) was explained completely by poor demand performance combined to increases in relative supply. To account for the increase in earnings of highly educated workers we introduced in the model factor biased technical change, which was suggested by the behavior of this group’s demand. We extended the model to permit different factors to be affected in diverse ways by technical change and use the college-high school earnings differential as the quantity whose evolution is to be explained. This exercise led us to conclude that changes in relative supplies combined with an almost constant rate of increase in the skill bias of technology towards highly educated workers explain the rise in relative earnings of that group of workers. This can be also interpreted as technological change increasing demand disproportionately for more educated workers in a constant fashion over time. International trade was shown to exert an equalizing effect on the overall distribution of labor earnings, because the demand shifts induced by trade were such that demand for less skilled workers grew relative to that for more skilled individuals as imports increased. This equalizing effect also is related to the fact that they favor female labor demand. However, trade contributed to increase the college-high school earnings differential. Finally, I argued that the bulk of the gains experienced by women were due to a reduction in labor market discrimination, and estimated reduced form earnings equations for men and women, showing that indeed discrimination is able to explain at least 70% of the gains made by women. 31 The semiparametric decomposition exercises carried out lend support to the above conclusions, but also provided two important additional pieces of evidence. First, the unprecedented increase in unemployment that started in 1996 has contributed to reduce inequality because it has eliminated low paid individuals from the distribution. This conclusion goes to the bottom of the problem: demand for labor in urban Colombia is becoming everyday more skill oriented, and additionally unemployment affects in a stronger fashion high school workers. The second point is related to education and its distribution across workers. As a rule the shifts of this variable increased measured inequality and reduced unexplained dispersion. This point is another way to see that the increases in the relative supply of college educated individuals is less than the one needed. 32 APPENDIX TABLE 4.1: CHANGE IN AVERAGE INCOME FOR AGGREGATTE GROUPS - URBAN 78-88 88-91 91-94 94-96 96-98 91-98 78-98 Groups Abs. Fw Total 31.9% -0.8% Men 25.7% -2.9% Women 36.2% 4.2% Low 13.8% 16.9% 7.5% -0.7% Medium Abs. Fw Abs. Fw -4.0% -8.7% 31.2% 28.6% -2.0% -6.7% 28.5% 27.2% -6.3% -12.8% 37.5% -6.3% -7.4% 16.9% Abs. Fw Abs. Fw Abs. Fw Abs. Fw -7.9% -9.2% 12.2% -0.2% 35.5% 16.6% 71.6% 5.7% -8.4% -9.6% 12.5% -2.4% 32.6% 12.2% 63.3% 1.6% 31.9% -6.5% -8.2% 12.8% 4.6% 44.9% 26.6% 84.9% 15.0% 17.4% -4.8% -6.1% -2.7% -1.5% 8.3% 8.5% 17.7% 17.5% -8.9% -10.7% 29.5% 27.6% -12.8% -13.7% 2.4% -1.5% 15.6% 8.5% 13.9% -3.8% High -22.9% -11.7% -5.1% -5.8% 36.7% 39.5% -2.3% -3.8% 3.8% 2.5% 38.7% 37.6% 7.0% 14.4% 0-10 exp 25.5% -3.9% 0.5% -5.7% 24.5% 24.6% -3.1% -3.2% 10.9% 0.6% 33.8% 21.3% 68.9% 10.1% 10-25 34.9% -1.3% -4.2% -8.7% 33.6% 30.8% -12.8% -17.1% 17.0% 3.7% 36.4% 15.8% 76.2% 4.4% 25 + 26.6% 3.2% -6.3% -11.4% 32.8% 29.3% -5.2% -6.8% 4.3% -6.7% 31.2% 13.0% 55.7% 3.2% 16.1% 12.3% -4.4% -5.7% 14.0% 15.2% -4.6% -6.5% -5.4% -5.1% 3.0% 2.3% 14.2% 8.3% 8.6% -1.1% -7.5% -9.8% 26.7% 24.6% -10.9% -11.7% 1.6% -3.9% 14.6% 5.7% 15.0% -5.7% -13.6% -15.3% -1.3% -1.9% 42.1% 41.1% -8.2% -8.6% 2.9% 1.4% 34.2% 30.8% 14.4% 8.7% 43.0% Men Low Medium High Women Low Medium High 22.7% 29.6% -10.3% -11.3% 22.3% 22.9% -3.7% -5.3% 4.9% 7.0% 23.5% 24.5% 35.8% 9.6% -0.1% -9.6% -12.4% 34.9% 33.8% -16.1% -17.6% 5.6% 3.5% 19.5% 14.1% 18.5% -0.2% -2.1% -10.7% -14.9% 36.0% 35.3% 9.8% 4.6% 4.8% 59.0% 55.7% 38.5% 29.7% -2.4% 11.7% 33 TABLE 4.2: AVERAGE INCOME BY DECIL - URBAN Decil 78 88 91 94 96 98 1 2 3 4 5 6 7 8 9 10 1,018.8 1,894.6 2,379.8 2,717.8 3,005.5 3,480.6 4,127.7 5,345.0 7,494.1 18,603.3 1,398.6 2,648.9 3,116.7 3,436.2 3,793.0 4,467.3 5,221.6 6,594.9 9,171.9 22,221.1 1,248.5 2,400.5 2,821.6 3,114.0 3,557.2 4,194.5 5,023.2 6,266.3 8,900.6 22,063.8 1,553.3 2,782.2 2,961.5 3,400.1 4,103.0 4,906.5 5,877.2 7,797.2 10,827.9 33,948.9 1,487.7 2,700.9 2,980.2 3,455.7 3,976.9 4,756.6 5,786.8 7,338.7 10,785.8 28,368.7 1,452.7 2,643.2 3,002.7 3,377.8 3,984.6 4,774.6 6,101.9 8,177.5 12,554.9 34,409.5 Total 4,666.7 6,155.7 5,911.8 7,757.8 7,141.1 8,010.3 TABLE 4.2A: CHANGES IN AVERAGE E ARNINGS DECIL - URBAN Decil 78-88 88-91 91-94 94-96 96-98 91-98 94-98 78-98 1 2 3 4 5 6 7 8 9 10 37.3% 39.8% 31.0% 26.4% 26.2% 28.3% 26.5% 23.4% 22.4% 19.4% -10.7% -9.4% -9.5% -9.4% -6.2% -6.1% -3.8% -5.0% -3.0% -0.7% 24.4% 15.9% 5.0% 9.2% 15.3% 17.0% 17.0% 24.4% 21.7% 53.9% -4.2% -2.9% 0.6% 1.6% -3.1% -3.1% -1.5% -5.9% -0.4% -16.4% -2.3% -2.1% 0.8% -2.3% 0.2% 0.4% 5.4% 11.4% 16.4% 21.3% 16.4% 10.1% 6.4% 8.5% 12.0% 13.8% 21.5% 30.5% 41.1% 56.0% -6.5% -5.0% 1.4% -0.7% -2.9% -2.7% 3.8% 4.9% 15.9% 1.4% 42.6% 39.5% 26.2% 24.3% 32.6% 37.2% 47.8% 53.0% 67.5% 85.0% Total 31.9% -4.0% 31.2% -7.9% 12.2% 35.5% 3.3% 71.6% 34 TABLE 4.3: FIXED WEIGHT RELATIVE CHANGE IN AVERAGE INCOME FOR AGGREGATTE GROUPS - RURAL Groups 78-88 88-91 91-94 94-96 96-98 91-98 78-98 Actual Predict Actual Predict Actual Predict Actual Predict Actual Predict Actual Predict Actual Predict Total 0.0% 0.0% 0.0% 0.0% 0.0% 0.0% 0.0% 0.0% 0.0% 0.0% 0.0% 0.0% 0.0% 0.0% Men 6.8% 1.7% 0.6% 1.0% -6.9% -2.0% 0.4% -1.5% -1.6% 1.0% -5.6% -2.9% -2.0% 0.0% -25.6% -6.3% -2.4% -3.9% 26.1% 7.4% -1.6% 5.7% 6.0% -4.0% 21.3% 10.9% 7.7% 0.0% -3.2% 8.9% 2.5% 6.0% 1.6% 14.3% 10.9% 29.2% 15.8% 21.4% 16.6% 1.8% -7.1% -1.7% -0.2% -1.0% -4.0% 14.7% 3.8% -7.1% 0.5% Women Uneducated 50.8% 3.9% -37.5% Primary -11.5% 3.5% Hs -16.2% -15.1% 20.5% 6.4% College -41.2% -28.8% 26.9% 12.0% 0-10 exp -15.3% 6.1% -15.7% 10-25 -13.3% 0.7% 14.7% 1.9% -3.9% -2.0% 1.9% 25+ 18.3% -2.9% -0.5% -7.4% -3.4% -8.0% -11.8% -9.8% -8.0% -15.9% -26.2% -2.6% 2.0% 9.5% -2.9% 2.7% 10.2% 8.6% 0.2% 10.5% 8.6% -14.7% -23.6% -5.9% 24.5% 3.1% 6.9% 9.3% -3.6% -6.5% 21.1% 7.7% -8.8% 0.6% 2.7% 2.4% 7.8% 5.6% -7.4% -2.2% -5.9% -6.9% -3.7% -0.4% -13.0% -11.0% -15.3% -14.1% 1.6% 8.4% 7.6% 9.1% 14.4% 13.4% Men Uneducated 66.8% 3.9% -40.7% 0.5% 7.8% 0.1% 4.1% 3.3% 20.7% 4.5% 18.1% 10.1% Primary -6.8% 6.2% 1.1% -9.7% -3.5% -0.2% -1.9% -5.4% 1.7% -11.3% -4.0% 0.5% -18.8% 2.0% -0.8% -4.2% -2.5% -4.3% -18.0% -7.2% -13.7% -24.2% 4.6% Hs -18.8% -20.0% 43.2% College -34.5% -25.4% 24.5% 12.8% 21.7% 1.5% 11.2% -5.5% 2.7% -3.6% -15.0% -5.4% -14.4% -12.3% -22.1% -21.4% -36.4% -39.3% Women Uneducated -21.3% 3.9% -22.9% -19.6% 14.2% 13.4% 14.1% 2.0% 28.2% 44.7% 67.2% 66.4% 36.3% 45.7% Primary -32.1% -8.8% 14.0% 3.0% Hs -10.6% -4.3% -29.0% -13.9% 88.0% College -49.8% -33.2% 30.0% 11.0% 4.7% 4.7% -6.3% 6.0% -0.1% 8.0% -10.6% 9.9% -0.9% 10.6% 7.6% -20.9% 10.7% -19.8% -28.2% 8.0% -9.6% -20.7% -30.5% -2.1% 25.6% 30.4% 38.3% 16.4% 53.0% 47.6% 13.6% -1.2% -3.3% 35 TABLE 4.4: ESTIMATION RESULTS EQUATION (9) - URBAN 78-88 Biased coeff elasticity significance R2 c.i coeff c.i elas el=1-Beta1 coeff elasticity significance R2 c.i coeff c.i elas el=1-Beta2 coeff elasticity significance R2 c.i coeff c.i elas 0.0013 0.9987 9.5% 10.0% 88-91 0.1686 0.8314 88.8% 15.8% 91-94 -0.1818 1.1818 73.4% 11.4% 94-96 96-98 0.0693 0.9307 26.4% 10.2% -0.1533 1.1533 94.6% 15.5% [-0.02,0.023] [0.041,0.379] [-0.507,0.143] [-0.388,0.526] [-0.366,-0.003] [0.978,1.019] [0.627,0.996] [0.865,1.5] [0.485,1.377] [1,1.361] 0.0217 0.9783 100.0% 55.6% 0.2312 0.7688 98.3% 21.5% -0.4303 1.4303 96.0% 18.7% 0.5584 0.4416 100.0% 21.8% -0.2035 1.2035 98.1% 21.1% [0.013,0.03] [0.049,0.414] [-0.772,-0.089] [0.202,0.914] [-0.391,-0.016] [0.967,0.987] [0.591,0.947] [1.098,1.763] [0.095,0.789] [1.02,1.386] 0.0132 0.9868 63.9% 11.8% 0.2157 0.7843 97.2% 19.8% -0.2953 1.2953 82.5% 13.9% 0.1554 0.8446 55.2% 11.2% -0.1932 1.1932 97.0% 16.4% [-0.017,0.043] [0.025,0.406] [-0.618,0.027] [-0.306,0.617] [-0.387,-0.012] [0.956,1.016] [0.599,0.97] [0.991,1.61] [0.395,1.294] [1.003,1.383] TABLE 4.4A: ESTIMATION RESULTS - URBAN (SECOND DIFFERENCES) 78-88 Biased coeff elasticity significance R2 c.i coeff c.i elas el=1-Beta1 coeff elasticity significance R2 c.i coeff c.i elas el=1-Beta2 coeff elasticity significance R2 c.i coeff c.i elas 0.0051 0.9949 21.0% 10.1% 88-91 0.0298 0.9702 97.8% 14.0% 91-94 0.1155 0.8845 35.1% 10.5% 94-96 -0.1083 1.1083 39.7% 10.4% 96-98 -0.0471 1.0471 31.4% 20.2% [-0.033,0.044] [0.005,0.055] [-0.392,0.623] [-0.536,0.32] [-0.412,0.318] [0.957,1.032] [0.946,0.995] [0.39,1.379] [0.691,1.625] [.691,1.403] 0.0628 0.9372 99.2% 31.5% 0.0469 0.9531 98.9% 20.5% 0.5056 0.4944 92.6% 22.7% -0.6043 1.6043 99.5% 25.7% -0.3648 1.3648 99.9% 39.4% [0.017,0.109] [0.011,0.083] [0.051,1.062] [-1.016,-0.192] [-0.578,-0.151] [0.892,0.982] [0.918,0.988] [-0.048,0.974] [1.203,2.006] [1.157,1.573] 0.0137 0.9863 57.3% 10.6% 0.0412 0.9588 99.1% 17.8% 0.2265 0.7735 59.7% 12.1% -0.2235 1.2235 71.6% 11.7% -0.1131 1.1131 57.6% 21.3% [-0.021,0.048] [0.011,0.072] [-0.314,0.767] [-0.639,0.192] [-0.476,0.25] [0.953,1.02] [0.929,0.988] [0.247,1.3] [0.819,1.628] [.76,1.466] 36 TABLE 4.5: CHANGES IN NET SUPPLIES AND E ARNINGS FOR AGGREGATED LEVELS OF SKILL - URBAN 78-88 Groups Men Women CS CD -0.07 -0.03 0.12 0.04 CNS 88-91 CW CS CD -0.04 -0.03 -0.03 0.00 0.09 0.04 0.05 0.00 CNS 91-94 CD CNS 94-96 CW CS CW CS CD CNS CW -0.03 -0.07 0.00 0.02 -0.02 0.24 -0.01 0.00 -0.01 -0.10 0.05 -0.14 0.00 -0.03 0.03 0.28 0.01 0.00 0.02 -0.09 Un -1.34 -0.22 -1.09 0.20 -0.14 -0.04 -0.10 -0.10 0.02 -0.01 0.03 0.25 -0.30 -0.02 -0.28 -0.15 Prim -0.41 -0.05 -0.36 0.15 -0.12 -0.03 -0.10 -0.08 -0.05 0.00 -0.05 0.15 -0.04 -0.01 -0.04 -0.06 Hsd 0.13 -0.03 0.17 0.03 -0.02 0.00 -0.03 -0.10 -0.04 0.00 -0.03 0.17 -0.01 -0.01 0.00 -0.11 Hs 0.75 0.02 0.73 -0.06 0.10 0.02 0.08 -0.10 0.10 0.00 0.10 0.28 0.06 0.00 0.06 -0.19 Cd 0.73 0.09 0.65 0.05 0.15 0.02 0.12 -0.16 -0.09 0.00 -0.08 0.32 0.07 0.01 0.06 -0.14 C+ 1.06 0.16 0.91 -0.12 0.14 0.02 0.12 -0.06 0.06 0.02 0.04 0.33 -0.01 0.03 -0.04 -0.04 0-5 -0.05 0.01 -0.06 0.00 -0.07 -0.02 -0.06 -0.04 -0.03 0.01 -0.04 0.20 -0.03 -0.03 0.01 0.00 5-10 0.14 0.00 0.14 -0.07 -0.05 0.00 -0.05 -0.07 -0.05 0.01 -0.06 0.24 -0.04 -0.02 -0.02 -0.05 10-25 25+ 0.14 0.00 0.14 -0.01 0.06 0.00 0.06 -0.09 0.03 0.00 0.03 0.27 -0.01 0.01 -0.02 -0.16 -0.22 -0.01 -0.21 0.03 -0.01 0.01 -0.02 -0.12 0.01 -0.01 0.02 0.26 0.06 0.02 0.03 -0.07 -1.47 -0.16 -1.30 0.11 -0.12 0.00 -0.11 0.01 0.12 0.00 0.12 0.18 -0.36 -0.01 -0.34 -0.20 -0.50 -0.09 -0.41 0.12 -0.13 0.00 -0.12 -0.06 -0.03 0.02 -0.05 0.14 -0.06 0.00 -0.06 -0.06 0.13 -0.06 0.19 0.02 -0.07 0.00 -0.07 -0.09 -0.02 0.01 -0.04 0.18 -0.02 -0.01 -0.01 -0.12 0.74 0.00 0.74 -0.07 0.10 0.01 0.09 -0.08 0.08 0.01 0.07 0.28 0.07 0.00 0.07 -0.18 0.69 0.07 0.62 0.07 0.04 0.01 0.03 -0.17 -0.02 0.01 -0.03 0.18 0.05 0.01 0.04 0.01 0.82 0.18 0.66 -0.17 0.10 0.00 0.10 -0.02 -0.02 0.04 -0.06 0.34 -0.01 0.03 -0.04 -0.09 Men Un Prim Hsd Hs Cd C+ Women Un Prim Hsd Hs Cd C+ -1.19 -0.31 -0.82 0.34 -0.16 -0.08 -0.07 -0.28 -0.12 -0.03 -0.08 0.38 -0.22 -0.03 -0.19 -0.09 -0.25 0.02 -0.26 0.25 -0.12 -0.07 -0.05 -0.11 -0.07 -0.04 -0.03 0.19 -0.01 -0.02 0.01 -0.05 0.15 0.02 0.13 0.06 0.06 0.01 0.05 -0.13 -0.06 -0.03 -0.02 0.14 0.00 -0.01 0.01 -0.07 0.77 0.05 0.72 -0.05 0.11 0.04 0.07 -0.13 0.13 -0.02 0.15 0.28 0.05 0.00 0.05 -0.20 0.78 0.11 0.68 0.00 0.27 0.04 0.23 -0.15 -0.15 -0.02 -0.14 0.53 0.10 0.01 0.09 -0.35 1.68 0.14 1.54 -0.02 0.21 0.04 0.17 -0.16 0.17 -0.01 0.18 0.30 -0.02 0.04 -0.05 0.09 37 TABLE 4.5: CONTINUATION Groups Men 96-98 CS CD CNS 91-98 CW CS CD CNS 78-98 CW CS CD CNS CW -0.03 -0.02 -0.01 -0.02 -0.04 0.00 -0.04 0.12 -0.14 -0.02 -0.11 0.02 Women 0.04 0.02 0.02 0.05 0.06 -0.01 0.06 0.24 0.22 0.03 0.20 0.14 Un 0.05 0.01 0.04 0.07 -0.23 -0.02 -0.21 0.16 -1.71 -0.28 -1.38 0.26 Prim -0.11 -0.02 -0.09 -0.02 -0.20 -0.02 -0.18 0.08 -0.74 -0.10 -0.63 0.15 Hsd -0.15 -0.04 -0.12 -0.04 -0.19 -0.04 -0.15 0.02 -0.08 -0.07 -0.01 -0.05 Hs 0.05 0.00 0.04 0.02 0.21 0.00 0.21 0.10 1.06 0.05 1.02 -0.06 Cd 0.06 0.05 0.01 -0.03 0.05 0.06 -0.01 0.16 0.93 0.18 0.76 0.04 C+ 0.32 0.07 0.25 0.02 0.37 0.12 0.25 0.32 1.57 0.31 1.30 0.13 0-5 0.00 0.00 0.00 -0.01 -0.05 -0.02 -0.03 0.18 -0.18 -0.03 -0.15 0.14 5-10 -0.11 -0.01 -0.10 0.02 -0.21 -0.02 -0.19 0.20 -0.12 -0.02 -0.10 0.06 10-25 0.04 0.00 0.04 0.04 0.06 0.00 0.06 0.15 0.26 0.00 0.26 0.04 25+ 0.00 0.00 0.00 -0.07 0.07 0.02 0.05 0.12 -0.16 0.02 -0.18 0.03 Men Un Prim Hsd Hs Cd C+ 0.05 0.01 0.04 0.12 -0.18 0.00 -0.18 0.10 -1.77 -0.16 -1.59 0.22 -0.15 -0.03 -0.12 -0.06 -0.25 -0.01 -0.23 0.02 -0.88 -0.11 -0.76 0.07 -0.19 -0.05 -0.14 -0.08 -0.23 -0.04 -0.19 -0.02 -0.17 -0.10 -0.07 -0.10 0.03 -0.01 0.04 0.02 0.17 -0.01 0.18 0.12 1.02 0.01 1.01 -0.04 0.07 0.03 0.04 -0.10 0.09 0.05 0.04 0.09 0.82 0.13 0.70 -0.01 0.34 0.06 0.28 0.01 0.31 0.13 0.19 0.27 1.23 0.31 0.96 0.08 Women Un Prim Hsd Hs Cd C+ 0.05 0.02 0.04 -0.01 -0.28 -0.04 -0.24 0.28 -1.63 -0.44 -1.06 0.35 -0.05 0.02 -0.06 0.07 -0.12 -0.04 -0.09 0.21 -0.49 -0.08 -0.40 0.36 -0.09 -0.01 -0.07 0.04 -0.14 -0.05 -0.09 0.11 0.07 -0.03 0.09 0.05 0.07 0.02 0.05 0.00 0.25 0.00 0.25 0.08 1.12 0.09 1.04 -0.10 0.06 0.08 -0.02 0.09 0.00 0.06 -0.05 0.26 1.06 0.23 0.86 0.11 0.31 0.09 0.22 0.05 0.46 0.12 0.35 0.44 2.34 0.29 2.08 0.26 38 TABLE 4.6: RELATIVE DEMAND SHIFTS FOR AGGREGATED GROUPS - URBAN Groups 78-88 88-91 91-94 94-96 96-98 Bet Within Tot Bet Within Tot Bet Within Tot Bet Within Tot Bet Within Tot Men -2.4% -0.3% -2.7% -0.4% 0.6% 0.2% 2.0% -0.3% 1.7% -0.9% 1.1% 0.2% -1.0% -0.8% -1.7% Women 3.7% -0.1% 3.6% 0.7% -1.0% -0.3% -3.1% 0.4% -2.7% 1.4% -1.6% -0.2% 1.6% Un -9.4% -12.9% -22.3% -3.1% -0.6% -3.8% -1.0% -0.5% -1.5% -1.7% -0.2% -1.9% 1.5% -0.1% 1.4% Prim -2.7% -2.5% -5.2% -2.2% -0.5% -2.7% 0.6% -0.7% -0.1% -1.1% 0.6% -0.5% -1.3% -0.3% -1.6% Hsd 1.1% -4.3% -3.2% -0.1% 0.6% 0.5% 0.0% -0.3% -0.3% -0.8% 0.3% -0.5% -1.9% -1.6% -3.5% Hs 2.4% 0.0% 2.4% 1.7% 0.7% 2.4% -0.8% 0.5% -0.4% 0.2% -0.4% -0.3% 1.0% -0.6% 0.4% Cd 2.4% 6.6% 8.9% 2.5% -0.2% 2.3% -0.7% 0.5% -0.2% 2.0% -0.9% 1.2% 3.7% 1.5% 5.3% C+ 1.9% 14.5% 16.4% 2.9% -1.2% 1.7% 0.5% 1.3% 1.8% 4.1% -0.8% 3.3% 3.5% 3.9% 7.3% 0-5 2.5% -1.5% 1.0% -0.4% -1.4% -1.8% -0.3% 1.0% 0.7% -0.2% -3.1% -3.2% 1.5% -1.2% 0.3% 5-10 1.5% -1.5% 0.0% 0.3% -0.5% -0.2% 0.1% 0.4% 0.6% -0.2% -1.6% -1.8% 0.3% -1.0% -0.7% 0.8% 2.4% 10-25 0.3% -0.6% -0.3% 0.3% 0.1% 0.4% 0.0% -0.2% -0.1% 0.3% 0.3% 0.6% -0.2% 0.0% -0.3% 25+ -3.0% 1.9% -1.0% -0.2% 0.9% 0.7% 0.0% -0.7% -0.7% -0.1% 2.5% 2.4% -0.7% 1.0% 0.3% Men Un Prim Hsd Hs Cd C+ -20.7% 5.0% -15.7% -1.4% 0.9% -0.5% 1.9% -1.9% 0.0% -3.2% 1.9% -1.3% -0.2% 1.5% 1.2% -6.5% -2.8% -9.2% -1.6% 1.3% -0.4% 3.2% -1.3% 1.9% -2.2% 2.3% 0.1% -2.2% -1.3% -3.5% -0.4% -5.5% -5.9% -0.8% 0.9% 0.1% 1.9% -0.5% 1.4% -1.5% 1.0% -0.5% -2.2% -2.5% -4.7% 0.8% -0.6% 0.2% 0.7% 0.5% 1.2% 0.4% 0.3% 0.7% -0.7% 0.4% -0.3% 0.1% -1.1% -1.0% 2.0% 5.2% 7.2% 1.1% -0.5% 0.6% 0.7% 0.6% 1.3% 1.5% -0.6% 0.9% 2.3% 0.8% 3.2% 2.2% 15.8% 17.9% 1.9% -1.4% 0.5% 2.0% 1.9% 3.9% 4.0% -0.9% 3.1% 1.6% 4.4% 6.0% Women Un Prim Hsd Hs Cd C+ 5.4% -36.4% -31.0% -5.4% -2.7% -8.1% -4.7% 1.4% -3.3% 0.2% -2.8% -2.6% 3.8% -2.3% 1.6% 3.9% -2.0% 1.8% -3.1% -3.5% -6.7% -4.0% 0.4% -3.6% 0.8% -2.5% -1.6% 0.3% 1.3% 1.7% 3.8% -2.2% 1.6% 1.1% 0.1% 1.2% -3.3% 0.0% -3.4% 0.5% -1.1% -0.6% -1.3% -0.1% -1.5% 4.5% 0.7% 5.1% 3.1% 0.9% 4.0% -2.4% 0.7% -1.7% 1.3% -1.6% -0.3% 2.2% 0.1% 2.2% 2.8% 8.1% 10.9% 4.1% 0.2% 4.3% -2.2% 0.4% -1.8% 2.7% -1.2% 1.5% 5.3% 2.3% 7.6% 1.6% 12.6% 14.2% 4.5% -0.9% 3.6% -1.7% 0.5% -1.2% 4.3% -0.6% 3.7% 6.2% 3.0% 9.2% 39 TABLE 4.6: CONTINUATION 91-98 Groups Bet Within 78-98 Tot Bet 0.3% Tot 0.1% 0.0% 0.1% Women -0.1% -0.5% -0.6% 4.3% -1.5% 2.8% Un -1.2% -0.8% -2.0% -13.8% -14.3% -28.1% Prim -1.8% -0.4% -2.2% -6.7% -3.4% -10.1% Hsd -2.7% -1.7% -4.4% -1.8% -5.3% -7.1% Hs 0.3% -0.6% -0.2% 4.5% 0.1% 4.6% Cd 5.1% 0.5% 5.7% 10.0% 7.6% 17.6% Men -2.7% Within -2.4% C+ 8.1% 4.4% 12.5% 12.9% 17.7% 30.6% 0-5 1.0% -3.2% -2.2% 3.1% -6.3% -3.1% 5-10 0.2% -2.3% -2.0% 2.0% -4.1% -2.2% 10-25 0.1% 0.0% 0.1% 0.7% -0.4% 0.2% -0.8% 2.7% 1.9% -4.0% 5.6% 1.6% -1.6% 1.5% -0.1% -23.7% 7.4% -16.3% -1.2% -0.2% -1.4% -9.3% -1.7% -11.0% 25+ Men Un Prim Hsd Hs Cd C+ -1.9% -1.9% -3.8% -3.1% -6.5% -9.6% -0.2% -0.4% -0.6% 1.3% -0.4% 0.8% 4.5% 0.9% 5.3% 7.6% 5.6% 13.2% 7.6% 5.4% 13.0% 11.7% 19.7% 31.4% -0.7% -3.7% -4.4% -0.8% -42.8% -43.6% -2.8% -0.8% -3.6% -2.1% -6.4% -8.5% -4.2% -1.2% -5.4% 0.7% -3.3% -2.7% 1.1% -0.8% 0.2% 8.6% 0.7% 9.3% Women Un Prim Hsd Hs Cd C+ 5.8% 0.2% 6.0% 12.8% 9.8% 22.6% 8.7% 2.9% 11.7% 14.8% 14.7% 29.5% 40 TABLE 4.7: IMPLICIT SUPPLY IN INTERNATIONAL TRADE FLOWS - URBAN Groups 1978 1988 1991 1994 1996 1998 All 7.56% 9.14% 4.30% 15.01% 11.73% 13.64% Men 6.74% 0.82% 8.20% 0.94% 6.18% -1.89% 13.26% 1.75% 10.34% 1.39% 11.19% 2.46% -0.15% 1.31% 2.79% 2.24% 0.58% 0.78% 0.01% 1.97% 2.90% 2.44% 0.73% 1.08% -0.04% 0.35% 1.20% 1.43% 0.51% 0.84% 0.08% 3.59% 4.86% 3.84% 1.07% 1.57% 0.07% 2.84% 3.77% 2.98% 0.84% 1.23% 0.09% 3.43% 4.46% 3.40% 0.92% 1.34% -0.12% 1.40% 2.60% 1.83% 0.43% 0.61% 0.03% 2.05% 2.76% 2.00% 0.54% 0.83% 0.00% 1.38% 2.11% 1.60% 0.43% 0.67% 0.09% 3.54% 4.53% 3.13% 0.79% 1.19% 0.07% 2.80% 3.50% 2.42% 0.62% 0.93% 0.09% 3.03% 3.80% 2.61% 0.66% 1.00% -0.02% -0.09% 0.19% 0.41% 0.15% 0.18% -0.01% -0.07% 0.14% 0.44% 0.19% 0.26% -0.05% -1.03% -0.90% -0.16% 0.08% 0.17% -0.01% 0.05% 0.33% 0.71% 0.28% 0.38% -0.01% 0.05% 0.27% 0.56% 0.23% 0.29% 0.01% 0.40% 0.66% 0.79% 0.27% 0.34% Women Uneducated Primary Hs dropouts Hs Some college College + Men Uneducated Primary Hs dropouts Hs Some college College + Women Uneducated Primary Hs dropouts Hs Some college College + 41 TABLE 4.7A: INTERNATIONAL TRADE DEMAND SHIFTS - URBAN Groups 1978 1988 1991 1994 1996 1998 Total 0.00 0.00 0.00 0.00 0.00 0.00 Men -0.15 -0.18 -0.23 -0.28 -0.22 -0.23 Women 0.23 0.27 0.36 0.43 0.34 0.35 Uneducated 0.38 0.35 0.22 0.50 0.40 0.51 Primary 0.12 0.12 0.13 0.16 0.12 0.14 Hs dropouts -0.11 -0.09 -0.02 -0.17 -0.13 -0.19 Hs -0.10 -0.10 -0.10 -0.13 -0.10 -0.12 Some college -0.02 -0.05 -0.12 -0.01 -0.01 0.03 0.01 -0.03 -0.13 0.03 0.02 0.07 0-5 exp -0.05 -0.05 -0.09 -0.06 -0.05 -0.04 5-10 -0.08 -0.08 -0.07 -0.10 -0.08 -0.10 10-25 -0.03 -0.03 -0.01 -0.04 -0.03 -0.04 25 + 0.12 0.12 0.11 0.16 0.12 0.15 College + Men Uneducated 0.38 0.30 0.15 0.41 0.31 0.42 Primary -0.01 -0.03 -0.10 -0.09 -0.08 -0.05 Hs dropouts -0.31 -0.32 -0.34 -0.53 -0.41 -0.47 Hs -0.29 -0.31 -0.36 -0.46 -0.36 -0.40 Some college -0.15 -0.20 -0.28 -0.24 -0.19 -0.18 College + -0.08 -0.14 -0.24 -0.13 -0.10 -0.08 Uneducated 0.38 0.41 0.31 0.63 0.50 0.63 Primary 0.33 0.39 0.52 0.59 0.47 0.49 0.31 Women Hs dropouts 0.23 0.30 0.55 0.46 0.36 Hs 0.14 0.18 0.24 0.29 0.23 0.24 Some college 0.14 0.13 0.07 0.26 0.20 0.27 College + 0.15 0.14 0.01 0.26 0.21 0.29 42 TABLE 4.8: CHANGES IN RELATIVE SUPPLIES DUE TO TRADE FLOWS Year Trade adj. supply-all True coll/High S Trade adj coll/High S 77 1.096 0.145 0.151 78 1.076 0.118 0.123 79 1.105 0.147 0.152 80 1.142 0.168 0.170 81 1.149 0.176 0.177 82 1.147 0.189 0.188 83 1.154 0.184 0.181 84 1.121 0.195 0.191 85 1.084 0.202 0.200 86 1.074 0.204 0.201 87 1.073 0.204 0.202 88 1.096 0.213 0.211 89 1.075 0.249 0.245 90 1.095 0.234 0.230 91 1.065 0.237 0.236 92 1.086 0.243 0.238 93 1.132 0.235 0.228 94 1.151 0.245 0.235 95 1.167 0.223 0.216 96 1.118 0.236 0.229 97 98 1.139 1.137 0.294 0.342 0.277 0.318 43 TABLE 4.9: TRADE, RELATIVE SUPPLIES AND RELATIVE EARNINGS, COLLEGE VS HIGH SCHOOL P r e d v a lu e s P r e d v a lu e s % change % change a d ju s t e d s u p u n a d ju s t e d s u p a d ju s t e d u n a d ju s t e d Year 77 0.9533 0.9575 na na 78 1.0894 1.0854 14.3% 13.4% 79 1.0040 1.0089 -7.8% -7.0% 80 0.9747 0.9757 -2.9% -3.3% 81 0.9828 0.9810 0.8% 0.5% 82 0.9796 0.9752 -0.3% -0.6% 83 1.0261 1.0177 4.7% 4.4% 84 1.0275 1.0195 0.1% 0.2% 85 1.0307 1.0307 0.3% 1.1% 86 1.0556 1.0545 2.4% 2.3% 87 1.0814 1.0826 2.4% 2.7% 88 1.0883 1.0923 0.6% 0.9% 89 1.0386 1.0452 -4.6% -4.3% 90 1.1003 1.1049 5.9% 5.7% 91 1.1151 1.1272 1.3% 2.0% 92 1.1377 1.1435 2.0% 1.4% 93 1.2388 1.2312 8.9% 7.7% 94 1.2017 1.1973 -3.0% -2.8% 95 1.2747 1.2698 6.1% 6.1% 96 1.2713 1.2722 -0.3% 0.2% 97 1.1998 1.1555 1.1954 1.1522 -5.6% -3.7% -6.0% -3.6% 98 TABLE 4.10: ESTIMATION RESULTS - RURAL 7 8 -8 8 8 8 -9 1 9 1 -9 4 9 4 -9 6 9 6 -9 8 B ia s e d c o e ff -0 .0 6 6 1 -1 .3 8 2 5 0 .0 8 3 0 0 .4 9 0 6 -0 .2 1 0 5 1 .0 6 6 1 2 .3 8 2 5 0 .9 1 7 0 0 .5 0 9 4 1 .2 1 0 5 s ig n ific a n c e 6 6 .3 % 9 6 .0 % 2 3 .2 % 9 3 .1 % 6 6 .0 % R 2 1 1 .1 % 2 3 .5 % 1 0 .1 % 1 6 .8 % 1 2 .6 % e la s tic ity e l= 1 -B e ta 1 c o e ff -0 .3 0 1 0 -1 .5 4 3 0 0 .4 6 9 2 0 .8 8 3 3 -0 .4 4 1 2 1 .3 0 1 0 2 .5 4 3 0 0 .5 3 0 8 0 .1 1 6 7 1 .4 4 1 2 s ig n ific a n c e 9 9 .5 % 9 8 .7 % 9 9 .9 % 9 9 .4 % 9 9 .0 % R 2 5 8 .0 % 3 1 .9 % 3 2 .4 % 3 5 .1 % 1 3 .4 % e la s tic ity TABLE 4.10A: INNER PRODUCTS DW*DNS 78-88 Biased -0.025927 88-91 91-94 0.074176 -0.018937 94-96 96-98 0.042164 0.006232 44 TABLE 4.11: CHANGES IN NET SUPPLIES AND E ARNINGS FOR AGGREGATED LEVELS OF SKILL - RURAL 78-88 Groups Men Women Un Prim 88-91 CS CD -0.07 0.01 -0.08 0.36 -0.03 0.21 0.25 0.30 -0.62 0.03 CNS CW 0.11 CS 0.11 CD CNS 91-94 CS CD 0.00 -0.03 0.08 0.00 0.01 -0.01 -0.24 0.02 0.03 0.00 0.04 -0.04 0.09 CNS 0.01 -0.63 0.71 -0.14 0.00 -0.14 -0.48 -0.10 -0.01 -0.09 0.01 0.31 0.00 0.02 0.00 94-96 CW 0.00 0.13 -0.03 CW CS CD CNS 0.05 -0.01 0.15 -0.17 -0.13 -0.03 -0.36 0.01 0.23 0.01 0.22 -0.20 0.00 -0.03 -0.18 0.08 0.00 0.08 -0.28 Hs 1.13 0.12 1.02 0.19 0.11 0.02 0.09 0.32 0.11 0.03 Coll 1.72 1.50 0.80 0.03 0.30 0.14 0.17 0.32 0.30 0.55 -0.14 -0.14 -0.51 -1.13 0-10 0.04 0.07 -0.02 0.23 0.00 0.01 -0.01 -0.09 -0.04 0.02 -0.06 0.32 0.01 0.01 10-25 25+ 0.06 -0.07 0.06 0.00 0.04 -0.11 0.41 -0.01 CW 0.06 -0.28 0.08 -0.28 -0.38 -0.09 -0.29 -0.39 0.63 -0.33 0.18 -0.10 -0.04 -0.06 -0.26 0.00 0.23 0.00 0.02 -0.02 -0.25 0.02 -0.04 0.06 -0.24 0.00 -0.01 0.03 0.03 0.01 0.04 -0.03 0.07 -0.35 0.02 -0.27 Men Un -0.65 -0.04 -0.61 0.76 -0.19 0.00 -0.19 -0.50 -0.04 -0.01 -0.03 0.01 0.27 0.03 0.24 -0.21 Prim -0.04 -0.01 -0.03 0.33 -0.02 0.00 -0.02 0.12 -0.02 0.00 -0.02 -0.20 0.10 0.01 0.09 -0.28 Hs 1.17 0.05 1.12 0.16 0.08 0.01 0.07 0.46 0.07 0.02 0.05 -0.54 -0.32 -0.05 -0.27 -0.28 Coll 1.42 1.26 0.60 -0.21 0.23 0.12 0.12 0.30 0.29 0.50 -0.11 -0.05 -0.68 -1.04 0.36 -0.54 Women Un 0.22 -0.69 0.21 0.03 0.01 0.02 -0.16 -0.30 -0.01 -0.30 Prim -0.49 0.39 0.08 0.31 0.12 0.08 0.01 0.08 Hs 1.05 0.28 0.80 0.29 0.17 0.04 0.13 -0.24 0.18 0.06 Coll 2.52 1.81 1.49 0.79 0.39 0.16 0.24 0.32 0.62 -0.17 -0.33 -0.32 -1.25 0.20 -0.05 0.37 0.04 -0.08 0.12 -0.10 0.01 -0.06 -0.02 -0.02 -0.04 0.02 -0.28 0.12 0.05 0.55 -0.51 -0.19 -0.30 -0.62 0.93 0.03 TABLE 4.11: CONTINUATION 96-98 Groups Men Women Un Prim Hs Coll 0-10 10-25 25+ 91-98 CD 78-98 CS CD CNS CW CS CNS CW CS CD CNS -0.001 0.00 -0.001 -0.04 0.000 0.04 0.127 0.19 0.046 -0.16 -0.006 -0.13 0.052 -0.03 -0.390 -0.02 -0.055 0.25 0.006 0.11 -0.061 0.054 0.15 0.26 CW 0.25 -0.06 -0.12 0.12 0.01 0.00 -0.02 -0.36 0.24 -0.06 -0.09 0.56 0.25 0.11 0.08 0.21 0.38 -0.01 -0.39 -0.09 0.01 -0.01 -0.09 -0.94 0.37 0.00 -0.30 2.72 0.07 -0.35 -0.59 -0.27 -0.38 0.02 0.85 1.93 0.02 0.00 0.06 0.70 -0.41 0.02 0.79 1.40 0.30 0.08 -0.08 0.09 -0.10 -0.01 0.06 -0.01 -0.01 -0.01 -0.09 0.00 0.07 0.11 0.19 0.11 -0.24 0.01 0.12 -0.03 -0.03 -0.03 -0.21 0.04 0.15 0.03 -0.30 -0.52 -0.20 0.08 0.05 0.05 0.03 0.01 -0.24 0.05 0.03 0.17 0.25 -0.09 0.25 -0.07 -0.11 0.30 0.00 0.00 0.00 -0.18 0.25 -0.07 -0.11 0.50 0.24 0.10 0.12 0.01 0.47 0.01 -0.36 -0.08 0.02 0.01 -0.03 -0.73 0.45 0.01 -0.33 1.21 0.03 -0.39 -0.70 -0.58 -0.37 -0.05 0.88 1.57 -0.02 0.00 0.03 0.66 -0.35 -0.04 0.86 1.06 0.29 0.06 -0.09 -0.49 0.28 -0.02 -0.12 -0.09 0.06 -0.02 -0.07 -0.58 0.22 0.00 -0.05 0.79 0.38 0.21 -0.04 0.42 0.02 -0.10 -0.46 -0.09 -0.02 -0.05 -0.20 -1.22 0.04 -0.04 -0.23 1.13 0.33 -0.09 -0.12 0.12 -0.45 0.37 0.77 2.81 0.21 0.03 0.12 0.75 -0.64 0.35 0.65 2.25 0.38 0.23 -0.07 1.29 Men Un Prim Hs Coll Women Un Prim Hs Coll 45 TABLE 4.12: IMPLICIT SUPPLY IN INTERNATIONAL TRADE FLOWS - RURAL Groups All Men Women Uneducated Primary Hs College Men Uneducated Primary Hs College Women Uneducated Primary Hs College 1978 1988 1991 1994 -31.02% -27.94% -3.09% -7.67% -20.99% -2.36% -0.01% -19.52% -16.76% -2.76% -4.87% -13.07% -1.56% -0.01% -19.22% -15.76% -3.46% -4.60% -12.83% -1.78% -0.01% -13.94% -11.84% -2.10% -3.83% -9.94% -0.29% 0.12% 1996 -7.82% -6.45% -1.37% -2.09% -5.40% -0.38% 0.04% 1998 -10.49% -9.16% -1.33% -2.72% -7.14% -0.65% 0.02% -6.89% -18.97% -2.08% 0.00% -4.03% -11.39% -1.34% 0.00% -3.77% -10.68% -1.31% 0.01% -3.22% -8.60% -0.15% 0.13% -1.65% -4.58% -0.27% 0.05% -2.28% -6.35% -0.56% 0.03% -0.78% -2.02% -0.28% -0.01% -0.84% -1.69% -0.22% -0.01% -0.84% -2.14% -0.46% -0.02% -0.61% -1.34% -0.14% -0.01% -0.44% -0.81% -0.11% -0.01% -0.44% -0.80% -0.09% -0.01% TABLE 4.12A: REALTIVE DEMAND SHIFTS DUE TO INTERNATIONA TRADE FLOWS - RURAL Groups Total 1978 0.00% 1988 0.00% 1991 0.00% 1994 0.00% 1996 0.00% 1998 0.00% Men Women 0.04% -0.16% 0.02% -0.06% 0.01% -0.03% 0.01% -0.04% 0.00% -0.01% 0.01% -0.04% Uneducated Primary Hs College 0.06% 0.03% -0.16% -0.30% 0.04% 0.02% -0.10% -0.19% 0.03% 0.02% -0.08% -0.19% 0.05% 0.02% -0.12% -0.21% 0.02% 0.01% -0.05% -0.10% 0.03% 0.01% -0.06% -0.12% 0-10 exp 10-25 25+ -0.06% -0.05% 0.00% -0.04% -0.03% 0.00% -0.03% -0.02% 0.01% -0.03% -0.03% 0.01% -0.02% -0.01% 0.00% -0.02% -0.02% 0.00% 0.10% 0.07% -0.12% -0.31% 0.04% 0.03% -0.07% -0.19% 0.03% 0.02% -0.07% -0.20% 0.05% 0.03% -0.13% -0.27% 0.02% 0.01% -0.05% -0.13% 0.03% 0.02% -0.05% -0.13% -0.10% -0.13% -0.25% -0.29% 0.03% -0.05% -0.15% -0.18% 0.03% 0.00% -0.10% -0.17% 0.02% -0.02% -0.11% -0.13% 0.04% -0.01% -0.06% -0.07% 0.01% -0.03% -0.09% -0.10% Men Uneducated Primary Hs College Women Uneducated Primary Hs College 46 TABLE 4.13: EVOLUTION OF MAIN COVARIATES 1978 1988 1991 1994 1996 1998 Occupation White Blue Domestic Self-emp Employer Men White Blue Domestic Self-emp Employer Women White Blue Domestic Self-emp Employer Avg. years of education Avg. years of experience % women 6.2 8.2 8.7 8.9 9.0 9.6 18.2 17.8 17.8 18.1 18.5 18.7 34.3% 38.4% 40.2% 40.3% 40.9% 42.7% 1978 1988 33.1% 35.5% 6.1% 22.3% 3.0% 25.3% 39.6% 6.5% 23.5% 5.2% 1991 24.7% 40.9% 4.8% 25.4% 4.2% 1994 1996 1998 25.1% 41.3% 4.8% 24.0% 4.9% 23.6% 40.6% 4.1% 27.1% 4.6% 19.8% 42.3% 4.4% 29.4% 4.1% 33.48 33.84 0.34 25.56 6.79 33.64 33.60 0.18 26.37 6.21 12.07 48.73 16.47 20.21 2.51 12.37 52.78 11.57 20.43 2.85 Erarnings Premium by Sector Compared to Retail Commerce Sector Agriculture coal Oil, gas Mining Food, bev, to Chemical Metallic pr Utilities Water Wholesale Communic Banking Insurance Real state Governm Services Social serv Entertainm Multilateral 88 0.293 0.404 0.541 0.333 0.136 0.169 0.167 0.280 0.317 0.313 0.206 0.248 0.280 0.177 0.225 0.138 0.168 0.243 0.912 94 0.220 0.656 0.261 0.534 0.099 0.118 0.000 0.128 0.244 0.265 0.144 0.219 0.318 0.161 0.190 0.111 0.065 0.192 0.834 96 0.228 0.418 0.470 0.094 0.071 0.061 0.000 0.284 0.303 0.215 0.324 0.257 0.335 0.181 0.188 -0.036 0.162 0.205 0.318 47 TABLE 4.14: DECOMPOSITION OF CHANGES IN EARNINGS DISTRIBUTION 1988-94 Statistic Gini Actual Emp Trade Educ Occup Gender p.a. s/d Total 0.074 -0.036 -0.009 0.054 0.021 -0.011 0.008 0.038 0.066 %cont 100.0% -47.9% -11.5% 72.2% 28.4% -15.0% 10.7% 51.8% 88.5% 90-10 0.076 -0.186 -0.426 0.469 0.196 -0.044 -0.065 0.153 0.098 %cont 100.0% -242.9% -557.1% 614.3% 257.1% -57.1% -85.7% 200.0% 128.6% 75-25 0.186 -0.218 0.011 0.251 -0.076 0.011 -0.011 0.164 0.131 %cont 100.0% -117.6% 5.9% 135.3% -41.2% 5.9% -5.9% 88.2% 70.6% Statistic Actual Emp 1994-96 Gini -0.033 %cont 90-10 %cont Trade Educ Occup Gender p.a. s/d Total -0.019 -0.027 0.112 -0.012 -0.012 0.021 0.004 0.067 100.0% 58.6% 82.4% -345.2% 37.4% 36.8% -64.1% -12.8% -206.8% 0.099 -0.154 -0.242 0.474 0.022 -0.066 0.154 -0.011 0.176 100.0% -155.6% -244.4% 477.8% 22.2% -66.7% 155.6% -11.1% 177.8% 0.044 75-25 -0.033 -0.264 0.397 0.000 -0.033 0.044 0.000 0.187 %cont 100.0% 800.0% -133.3% -1200.0% 0.0% 100.0% -133.3% 0.0% -566.7% Statistic Actual Emp Trade Gender p.a. 1996-98 Gini %cont Educ Occup s/d Total 0.041 -0.011 -0.031 0.103 0.012 -0.007 0.009 0.000 0.076 100.0% -26.1% -76.2% 251.2% 30.4% -17.1% 22.7% -0.7% 184.3% 90-10 0.215 -0.108 -0.343 0.421 0.186 0.029 0.000 -0.010 0.176 %cont 100.0% -50.0% -159.1% 195.5% 86.4% 13.6% 0.0% -4.5% 81.8% 75-25 0.078 -0.245 -0.020 0.440 -0.039 0.010 0.000 0.010 0.157 %cont 100.0% -312.5% -25.0% 562.5% -50.0% 12.5% 0.0% 12.5% 200.0% p.a.: Personal Attributes 48 TABLE 4.15: DECOMPOSITION OF CHANGE IN E ARNINGS DISTRIBUTION Statistic Sd wages %cont sd resid %cont coll/rest %cont Actual 0.011 100.0% Emp 0.005 Trade -0.026 46.2% -233.7% 1988-94 Educ Occup 0.072 -0.034 Gender p.a. s/d Total -0.018 0.023 0.058 0.080 640.9% -301.1% -162.9% 207.0% 516.5% 713.0% 0.004 -0.011 -0.001 -0.048 0.065 -0.001 -0.018 -0.008 -0.013 100.0% -0.8% -27.9% -12.1% -20.7% 5.9% -17.0% -0.8% -73.3% 0.024 0.021 -0.018 0.174 -0.043 -0.062 0.090 0.184 0.346 100.0% 88.1% -74.3% 719.5% -177.9% -257.7% 370.5% Actual Emp Trade Educ 758.4% 1426.8% 1994-96 Statistic Sd wages %cont sd resid %cont coll/rest %cont Statistic Sd wages %cont sd resid %cont coll/rest %cont Occup Gender p.a. s/d Total 0.127 0.001 -0.083 -0.021 -0.066 0.022 -0.049 -0.003 -0.197 100.0% 1.1% -65.8% -16.2% -51.8% 17.4% -38.4% -2.2% -155.8% 0.068 -0.002 -0.034 -0.007 -0.024 0.001 -0.009 -0.001 -0.075 100.0% -3.1% -49.5% -9.6% -35.0% 1.8% -13.1% -2.1% -110.7% -0.003 0.055 -0.008 0.019 -0.034 0.098 54.2% -129.0% 229.5% -660.6% 0.056 0.012 100.0% -0.015 20.5% -370.8% -381.0% -84.0% Actual Emp Trade 1996-98 Educ Occup Gender p.a. s/d Total 0.089 0.021 -0.023 0.197 -0.056 -0.076 0.101 0.183 0.345 100.0% 23.1% -25.7% 220.7% -63.4% -85.9% 113.8% 205.2% 387.9% 0.011 0.018 -0.074 0.245 -0.022 -0.072 0.124 0.269 0.488 100.0% 162.7% -678.6% 2232.1% -197.7% -652.6% 1133.0% 2457.8% 4456.7% 0.028 0.009 -0.014 0.173 100.0% 31.0% -50.6% 622.9% -0.009 -0.068 0.104 -32.5% -242.4% 373.2% 0.228 0.424 819.8% 1521.4% 49 FIGURE 4.1: CHANGES IN URBAN EARNINGS FOR AGGREGATE EDUCATION GROUPS-ABSOLUTE 1.3 Earnings 1.1 0.9 0.7 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 Year Low Medium High FIGURE 4.1A: CHANGE IN URBAN EARNINGS FOR AGGREGATE EDUCATION GROUPS – FIXED WEIGHT Fixed Weight Earnings 1.3 1.2 1.1 1 0.9 0.8 0.7 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 Year Low Med High 50 FIGURE 4.1B: URBAN EDUCATION DIFFERENTIALS-FIXED WEIGHT 1.2 Differential 1.1 1 0.9 0.8 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 Year Coll-low Coll-int FIGURE 4.1C: GENDER DIFFERENTIAL BY EDUCATION LEVEL-FIXED WEIGHT 0.7 Differential 0.6 0.5 0.4 0.3 0.2 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 Year Low Med High 51 FIGURE 4.2: OBSERVABLE INEQUALITY-URBAN 1.4 1.3 Differential 1.2 1.1 1 0.9 0.8 0.7 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 Year 90-10 90-50 50-10 75-25 FIGURE 4.2A: RESIDUAL INEQUALITY-URBAN 1.3 Differential 1.2 1.1 1 0.9 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 Year 90-10 90-50 50-10 75-25 52 FIGURE 4.3: OBSERVABLE INEQUALITY-RURAL 1.7 Differential 1.5 1.3 1.1 0.9 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 Year 90-10 90-50 50-10 75-25 FIGURE 4.3A: RESIDUAL INEQUALITY-RURAL 1.9 Differential 1.7 1.5 1.3 1.1 0.9 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 Year 90-10 90-50 50-10 75-25 53 FIGURE 4.4: PERCENTAGE CHANGES IN EARNINGS AND NET DEMAND BY SKILL GROUP. 1978-88 1.6 Earnings 1.2 0.8 0.4 0 -0.4 -10.5 -8.5 -6.5 -4.5 -2.5 -0.5 Net Demand 1988-91 Earnings 0.4 0.2 0 -0.2 -0.4 -0.6 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 Net Demand 1991-94 Earnings 1.4 1 0.6 0.2 -0.2 -3.8 -3.3 -2.8 -2.3 -1.8 -1.3 -0.8 -0.3 0.2 Net Demand 54 FIGURE 4.4: CONTINUATION 1994-96 Earnings 0.8 0.4 0 -0.4 -0.8 -0.5 -0.3 -0.1 0.1 0.3 0.5 0.7 Net Demand 1996-98 0.4 Earnings 0.3 0.2 0.1 0 -0.1 -0.2 -0.3 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 Net Demand 55 FIGURE 4.5: ACTUAL VS PREDICTED COLLEGE-HIGH SCHOOL EARNINGS DIFFERENTIALS-FIXED WEIGHT 1.4 Differential 1.3 1.2 1.1 1 0.9 0.8 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 95 96 97 98 Time Actual Predicted FIGURE 4.5A: COLLEGE-HS DIFFERENTIAL VS TREND 1.4 Log diff 1.2 1 0.8 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 Time Diff Trend 56 FIGURE 4.5B: TIME PATH OF G(T) AND TRENDS 0.8 0.4 g(t) 0 -0.4 -0.8 -1.2 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 Time el=1.476 el=1.65 Trend Trend el=1.3 el=3 Trend Trend FIGURE 4.5C: RELATIVE SUPPLY OF COLLEGE VS HIGH SCHOOL Log relative suppply 1.1 0.9 0.7 0.5 0.3 0.1 -0.1 -0.3 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 Time Det supply Supply 57 FIGURE 4.6: MEASURED DISCRIMINATION (MALE VS FEMALE) 1.9 1.8 Male/female 1.7 1.6 1.5 1.4 1.3 1.2 1.1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Female's Earnings Support-5% percentiles 1978 1991 1998 58 FIGURE 4.7: DECOMPOSITION OF CHANGES IN DENSITY FUNCTIONS, 1988-94 Actual Densities 1.6 1988 1994 1.2 f(.) 5th 0.8 25th 75th 0.4 95th 0 2.5 5 7.5 10 12.5 Log of Earnings Trade Counterfactual 1.6 1994 trade f(.) 1.2 5th 0.8 25th 75th 0.4 95th 0 2.5 5 7.5 10 12.5 Log of Earnings Personal Attributes Counterfactual 1.6 trade f(.) 1.2 p.a. 5th 0.8 25th 75th 0.4 95th 0 2.5 5 7.5 10 12.5 Log of Earnings 59 FIGURE 4.7: COTINUATION. Counterfactual Supply & Demand 1.6 f(.) 1.2 p.a. s&d 0.8 5th 25th 0.4 75th 95th 0 2.5 5 7.5 10 12.5 Log of earnings Residual 1.6 s&d 1.2 f(.) 1988 5th 0.8 25th 75th 0.4 95th 0 2.5 5 7.5 10 Log of earnings 12.5 60 FIGURE 4.7A: DECOMPOSITION OF CHANGES IN DENSITY FUNCTIONS, 1994-96 Actual Densities 1.2 1994 1996 0.8 f(.) 5th 25th 0.4 75th 95th 0 2.5 5 7.5 10 12.5 Log of Earnings Trade Counterfactual 1.2 0.8 f(.) 1996 trade 5th 0.4 25th 75th 0 95th 2.5 5 7.5 10 12.5 Log of Earnings Personal Attributes Counterfactual 1.2 trade p.a. 0.8 f(.) 5th 25th 75th 0.4 95th 0 2.5 5 7.5 10 12.5 Log of Earnings 61 FIGURE 4.7A: COTINUATION. Counterfactual Supply & Demand 1.2 p.a. 0.8 s&d f(.) 5th 25th 0.4 75th 95th 0 2.5 5 7.5 10 Log of earnings 12.5 Residual 1.2 s&d 0.8 1994 f(.) 5th 25th 0.4 75th 95th 0 2.5 5 7.5 10 12.5 Log of earnings 62 FIGURE 4.7B: DECOMPOSITION OF CHANGES IN DENSITY FUNCTIONS, 1996-98 Actual Densities 1.2 f(.) 0.8 1996 1998 0.4 0 2.5 5 7.5 Log of Earnings 10 12.5 Trade Counterfactual 1.2 f(.) 0.8 1998 trade 0.4 0 2.5 5 7.5 10 12.5 Log of Earnings Personal Attributes Counterfactual 1.2 f(.) 0.8 trade p.a. 0.4 0 2.5 5 7.5 10 12.5 Log of Earnings 63 FIGURE 4.7B: COTINUATION. Counterfactual Supply & Demand 1.2 f(.) 0.8 p.a. s&d 0.4 0 2.5 5 7.5 Log of earnings 10 12.5 Residual 1.2 f(.) 0.8 s&d 1996 0.4 0 2.5 5 7.5 10 Log of earnings 12.5 64 REFERENCES Amemiya, T. (1985). Advanced Econometrics. Harvard University Press. Cambridge, MA. Bhagwati, J. and V. Dehejia (1994). Freer Trade and Wages of the Unskilled, Is Marx Striking Again?. In J. Bhagwati and M. Kosters (eds.). Trade and Wages: Leveling Wages Down?. American Enterprise Institute. Washington, DC. Bejarano, J. (1992). Productividad y Empleo en el Campo Colombiano. Tercer Mundo Editores. Santafé de Bogotá, DC. Colombia. Bound, J. and G. Johnson (1992). Changes in the structure of Wages in the 1980s: An Evaluation of Alternative Explanations. American Economic Review. 82: 371-92. Borjas, G., Freeman, R. and L. Katz (1992) (eds.). Immigration and the Work Force: Economic Consequences for the United States and the Source Areas. University of Chicago Press. Chicago, Il. Borjas, G., Freeman, R. and L. Katz (1996). Searching for the Effect of Immigration in the Labor Market. American Economic Review. 84(may): 10-16. Borjas, G., Freeman, R. and L. Katz (1998). How Much do Immigration and Trade Affect Labor Market Outcomes?. Brookings Papers on Economic Activity. 1, 1-67. Caligiuri, P. and C.R. Rao (1993). Analysis of Ordered Data through Appropriate Scaling. In C.R. Rao (ed.) Handbook of Statistics 9. North-Holland, Amsterdam, Netherlands. Collins, S. (ed.), (1998). Imports, Exports and the American Worker. The Brookings Institution. Washington, D.C. Cline, W. (1997). Trade and Income Distribution. Institute for International Economics. Washington, D.C. Deardorff, A. and R. Staiger (1988). An Interpretation of the Factor Content of Trade. Journal of International Economics. 24: 93-107. DiNardo, J., Fortin, N. and T. Lemieux (1996). Labor Market Institutions and the Distribution of Wages, 1973-1992: A Semiparametric Approach. Econometrica. 64(5): 1001-1044. Oxford, UK. DNP (1995). Guía del Usuario del Banco de Fuentes Primarias, BFP. DNP. Santafé de Bogotá DC, Colombia. DNP (1991-99). Indicadores de Coyuntura Económica. Various numbers. Santafé de Bogotá, DC. 65 Freeman, R. (1975). Overinvestment in College Training?. Journal of Human Resources. X, 287311. Freeman, R. (1980). An Empirical Analysis of the Fixed Coefficient Manpower Requirements Model, 1960-1970. Journal of Human Resources. XV, 176-99. Freeman, R. (1998). Will Globalization Dominate Labor Market Outcomes?. In S. Collins (ed.). Imports, Exports and the American Worker. Brookings Institution. Washington, DC. Greene, W.H. (1997). Econometric Analysis. Prentice Hall. London, U.K. Heckman, J. (1976). The Common Structure of Statistical Models of Truncation, Sample Selection, and Limited Dependent Variables and a Simple Estimators for Such Models. Annals of Economic and Social Measurement. 5: 475-492. Heckman, J. (1979). Sample Selection Bias as a Specification Error. Econometrica.47: 153-161. Hogg, R.V. and A.T. Craig (1978). Introduction to Mathematical Statistics, Fourth Edition. Macmillan Publishing Co., Inc. and Collier Macmillan Publishers. Juhn, C., Murphy, K. and B. Pierce (1993). Wage Inequality and the Rise in Returns to Skill. Journal of Political Economy. 101(3), 410-42. Katz, L. and K. Murphy (1992). Changes in Relative Wages 1963-87: Supply and Demand Factors. Quarterly Journal of Economics. 107: 35-78. Kosters, M. (ed.), (1991). Workers and Their Wages: Changes Patterns in the United States.. The AEI Press. Washington, D.C. Krugman, P. (1995). Technology, Trade and Factor Prices. NBER Working Paper No 5355. Cambridge, MA. Murphy, K., Riddell, C. and P. Romer. (1998). Wages, Skill and Technology in the United States and Canada. NBER Working Paper 6638. National Bureau of Economic Research. Cambridge, MA. Murphy, K. and F. Welch (1991). The Role of International Trade in Wage Differentials. In M. Kosters (ed.) Workers and Their Wages: Changing Patterns in the United States. The AEI Press, Washington, DC. Oaxaca, R. (1973). Male-Female Wage Differentials in Urban Labor Markets. International Economic Review. 14: 673-709. Sánchez, F. and J. Núñez (1998). Educación y Salarios Relativos en Colombia 1976-1995. Determinantes, Evolución e Implicaciones para la Distribución del Ingreso. Archivos de Macroeconomía. Documento 74. DNP. Santafé de Bogotá, DC. Colombia. Sánchez, F. and J. Núñez (1998a). Descomposición de la desigualdad del Ingreso Laboral Urbano 66 en Colombia: 1976-1997. Archivos de Macroeconomía. Documento 86. DNP. Santafé de Bogotá, DC. Colombia. Santamaría, M. (1997). Describing the Evolution of Income Inequality: Colombia 1978-95. First Dissertation Paper. Mimeo. Washington, D.C. Santamaría, M. (1999). Nonparametric Density Estimation and Regression: an Application to the Study of Income Inequality and Poverty, Colombia (1978-1996). Second Dissertation Paper. Mimeo. Washington, D.C. Stata Corp (1999). Reference Manual, Release 6.0. Stata Press. College Station, TX. Stata Corp (1999). User’s Guide, Release 6.0. Stata Press. College Station, TX. Vélez, C.E., Bouillon, C. and A. Kugler (1999). The Reversal of Inequality Gains in Urban Colombia, 1978-1995: A Combination of Persistent and Fluctuating Forces. Mimeo. Interamerican Development Bank. Washington, D.C. 67 ARCHIVOS DE ECONOMIA No Título Autores Fecha 1 La coyuntura económica en Colombia y Venezuela Andrés Langebaek Patricia Delgado Fernando Mesa Parra Octubre 1992 2 La tasa de cambio y el comercio colombo-venezolano Fernando Mesa Parra Andrés Langebaek Noviembre 1992 3 ¿Las mayores exportaciones colombianas de café redujeron el precio externo? Carlos Esteban Posada Andrés Langebaek Noviembre 1992 4 El déficit público: una perspectiva macroeconómica Jorge Enrique Restrepo Juan Pablo Zárate Carlos Esteban Posada Noviembre 1992 5 El costo de uso del capital en Colombia Mauricio Olivera Diciembre 1992 6 Colombia y los flujos de capital privado a América Latina Andrés Langebaek Febrero 1993 7 Infraestructura física. “Clubs de convergencia” y crecimiento económico José Dario Uribe Febrero 1993 8 El costo de uso del capital: una nueva estimación (Revisión) Mauricio Olivera Marzo 1993 9 Dos modelos de transporte de carga por carretera Carlos Esteban Posada Edgar Trujillo Ciro Alvaro Concha Juan Carlos Elorza Marzo 1993 10 La determinación del precio interno del café en un modelo de optimización intertemporal Carlos Felipe Jaramillo Carlos Esteban Posada Edgar Trujillo Abril 1993 11 El encaje óptimo Edgar Trujillo Ciro Carlos Esteban Posada Mayo 1993 12 Crecimiento económico, “Capital humano” y educación: la teoría y el caso colombiano posterior a 1945 Carlos Esteban Posada Junio 1993 13 Estimación del PIB trimestral según los componentes del gasto Rafael Cubillos Junio 1993 Fanny Mercedes Valderrama 14 Diferencial de tasas de interés y flujos de capital en Colombia (1980-1993) Andrés Langebaek 15 Empleo y capital en Colombia: nuevas estimaciones (1950-1992) Adriana Barrios Septiembre 1993 Marta Luz Henao Carlos Esteban Posada Fanny Mercedes Valderrama Diego Mauricio Vásquez Agosto 1993 ARCHIVOS DE ECONOMIA No Título Autores Fecha 16 Productividad, crecimiento y ciclos en la economía colombiana (1967-1992) Carlos Esteban Posada Septiembre 1993 17 Crecimiento económico y apertura en Chile y México y perspectivas para Colombia Fernando Mesa Parra Septiembre 1993 18 El papel del capital público en la producción, inversión y el crecimiento económico en Colombia Fabio Sánchez Torres Octubre 1993 19 Tasa de cambio real y tasa de cambio de equilibrio Andrés Langebaek Octubre 1993 20 La evolución económica reciente: dos interpretaciones alternativas Carlos Esteban Posada Noviembre 1993 21 El papel de gasto público y su financiación en la coyuntura actual: algunas implicaciones complementarias Alvaro Zarta Avila Diciembre 1993 22 Inversión extranjera y crecimiento económico Alejandro Gaviria Javier Alberto Gutiérrez Diciembre 1993 23 Inflación y crecimiento en Colombia Alejandro Gaviria Carlos Esteban Posada Febrero 1994 24 Exportaciones y crecimiento en Colombia Fernando Mesa Parra Febrero 1994 25 Experimento con la vieja y la nueva teoría del crecimiento económico (¿porqué crece tan rápido China?) Carlos Esteban Posada Febrero 1994 26 Modelos económicos de criminalidad y la posibilidad de una dinámica prolongada Carlos Esteban Posada Abril 1994 27 Regímenes cambiarios, política macroeconómica y flujos de capital en Colombia Carlos Esteban Posada Abril 1994 28 Comercio intraindustrial: el caso colombiano Carlos Pombo Abril 1994 29 Efectos de una bonanza petrolera a la luz de un modelo de optimización intertemporal Hernando Zuleta Juan Pablo Arango Mayo 1994 30 . Crecimiento económico y productividad en Colombia: una perspectiva de largo plazo (1957-1994) Sergio Clavijo Junio 1994 31 Inflación o desempleo: ¿Acaso hay escogencia en Colombia? Sergio Clavijo Agosto 1994 ARCHIVOS DE ECONOMIA No Título Autores Fecha 32 La distribución del ingreso y el sistema financiero Edgar Trujillo Ciro Agosto 1994 33 La trinidad económica imposible en Colombia: estabilidad cambiaria, independencia monetaria y flujos de capital libres Sergio Clavijo Agosto 1994 34 ¿’Déjà vu?: tasa de cambio, deuda externa y esfuerza exportador en Colombia. Sergio Clavijo Mayo 1995 35 La crítica de Lucas y la inversión en Colombia: nueva evidencia Mauricio Cárdenas Mauricio Olivera Septiembre 1995 36 Tasa de Cambio y ajuste del sector externo en Colombia Fernando Mesa Parra Dairo Estrada Septiembre 1995 37 Análisis de la evolución y composición del Sector Público Mauricio Olivera G. Septiembre 1995 Manuel Fernando Castro Q. Fabio Sánchez T. 38 Incidencia distributiva del IVA en un modelo del ciclo de vida Juan Carlos Parra Osorio Fabio José Sánchez T. Octubre 1995 39 Por qué los niños pobres no van a la escuela? (Determinantes de la asistencia escolar en Colombia) Fabio Sánchez Torres Jairo Augusto Núñez M. Noviembre 1995 40 Matriz de Contabilidad Social 1992 Fanny M. Valderrama Javier Alberto Gutiérrez Diciembre 1995 41 Multiplicadores de Contabilidad Derivados de la Matriz de Contabilidad Social Javier Alberto Gutiérrez Fanny M. Valderrama G. Enero 1996 42 El ciclo de referencia de la economía colombiana Martin Maurer María Camila Uribe S. Febrero 1996 43 Impacto de las transferencias intergubernamentales en la distribución interpersonal del ingreso en Colombia Juan Carlos Parra Osorio Marzo 1996 44 Auge y colapso del ahorro empresarial en Colombia 1983-1994 Fabio Sánchez Torres Abril 1996 Guillermo Murcia Guzmán Carlos Oliva Neira 45 Evolución y comportamiento del gasto público en Colombia 1950-1994 Cielo María Numpaque Ligia Rodríguez Cuestas Mayo 1996 46 Los efectos no considerados de la apertura económica en el mercado laboral industrial Fernando Mesa Parra Javier Alberto Gutiérrez Mayo 1996 47 Un modelo de Financiamiento óptimo de un aumento permanente en el gasto público: Una ilustración con el caso colombiano. Alvaro Zarta Avila Junio 1996 ARCHIVOS DE ECONOMIA No Título Autores Fecha 48 Estadísticas descriptivas del mercado laboral masculino y femenino en Colombia: 1976 -1995 Rocío Ribero M. Carmen Juliana García B. Agosto 1996 49 Un sistema de indicadores líderes para Colombia Martín Maurer María Camila Uribe Javier Birchenall Agosto 1996 50 Evolución y determinantes de la productividad en Colombia: Un análisis global y sectorial Fabio Sánchez Torres Jorge Iván Rodríguez Jairo Núñez Méndez Agosto 1996 51 Gobernabilidad y Finanzas Públicas en Colombia César A. Caballero R Noviembre 1996 52 Tasas Marginales Efectivas de Tributación en Colombia Mauricio Olivera G. Noviembre 1996 53 Un modelo keynesiano para la economía colombiana Fabio José Sánchez T. Clara Elena Parra Febrero 1997 54 Trimestralización del Producto Interno Bruto por el lado de la oferta. Fanny M. Valderrama Febrero 1997 55 Poder de mercado, economías de escala, complementariedades intersectoriales y crecimiento de la productividad en la industria colombiana. Juán Mauricio Ramírez Marzo 1997 56 Estimación y calibración de sistemas flexibles de gasto. Orlando Gracia Gustavo Hernández Abril 1997 57 Mecanismos de ahorro e Inversión en las Empresas Públicas Colombianas: 1985-1994 Fabio Sánchez Torres Guilllermo Murcia G. Mayo 1997 58 Capital Flows, Savings and investment in Colombia 1990-1996 José Antonio Ocampo G. Camilo Ernesto Tovar M. Mayo 1997 59 Un Modelo de Equilibrio General Computable con Competencia imperfecta para Colombia Juan Pablo Arango Orlando Gracia Gustavo Hernández Juan Mauricio Ramírez Junio 1997 60 El cálculo del PIB Potencial en Colombia Javier A. Birchenall J. Julio 1997 61 Determinantes del Ahorro de los hogares. Explicación de su caída en los noventa. Alberto Castañeda C. Gabriel Piraquive G. Julio 1997 62 Los ingresos laborales de hombres y mujeres en Colombia: 1976-1995 Rocío Ribero Claudia Meza Agosto 1997 ARCHIVOS DE ECONOMIA No Título Autores Fecha 63 Determinantes de la participación laboral de hombres y mujeres en Colombia: 1976-1995 Rocío Ribero Claudia Meza Agosto 1997 64 Inversión bajo incertidumbre en la Industria Colombiana: 1985-1995 Javier A. Birchenall Agosto 1997 65 Modelo IS-LM para Colombia. Relaciones de largo plazo y fluctuaciones económicas. Jorge Enrique Restrepo Agosto 1997 66 Correcciones a los Ingresos de las Encuestas de hogares y distribución del Ingreso Urbano en Colombia. Jairo A. Núñez Méndez Jaime A. Jiménez Castro Septiembre 1997 67 Ahorro, Inversión y Transferencias en las Entidades Territoriales Colombianas Fabio Sánchez Torres Mauricio Olivera G. Giovanni Cortés S. Octubre 1997 68 Efectos de la Tasa de cambio real sobre la Inversión industrial en un Modelo de transferencia de precios Fernando Mesa Parra Leyla Marcela Salguero Fabio Sánchez Torres Octubre 1997 69 Convergencia Regional: Una revisión del caso Colombiano. Javier A. Birchenall Guillermo E. Murcia G. Octubre 1997 70 Income distribution, human capital and economic growth in Colombia. Javier A. Birchenall Octubre 1997 71 Evolución y determinantes del Ahorro del Gobierno Central. Fabio Sánchez Torres Ma. Victoria Angulo Noviembre 1997 72 Macroeconomic Perforrmance and Inequality in Colombia: 1976-1996 Raquel Bernal Mauricio Cárdenas Jairo Núñez Méndez Fabio Sánchez Torres Diciembre 1997 73 Liberación comercial y salarios en Colombia: 1976-1994 Donald Robbins Enero 1998 74 Educación y salarios relativos en Colombia: 1976-1995 Determinantes, evolución e implicaciones para la distribución del Ingreso Jairo Núñez Méndez Fabio Sánchez Torres Enero 1998 75 La tasa de interés “óptima” Carlos Esteban Posada Edgar Trujillo Ciro Febrero 1998 76 Los costos económicos de la criminalidad y la violencia en Colombia: 1991-1996 Edgar Trujillo Ciro Martha Elena Badel Marzo 1998 77 Elasticidades Precio y Sustitución para la Industria Colombiana Juán Pablo Arango Orlando Gracia Gustavo Hernández Marzo 1998 ARCHIVOS DE ECONOMIA No Título Autores Fecha 78 Flujos Internacionales de Capital en Colombia: Un enfoque de Portafolio Ricardo Rocha García Fernando Mesa Parra Marzo 1998 79 Macroeconomía, ajuste estructural y equidad en Colombia: 1978-1996 José Antonio Ocampo María José Pérez Camilo Ernesto Tovar Francisco Javier Lasso Marzo 1998 80 La Curva de Salarios para Colombia. Una Estimación de las Relaciones entre el Desempleo, la Inflación y los Ingresos Laborales, 1984- 1996. Fabio Sánchez Torres Jairo Núñez Méndez Marzo 1998 81 Participación, Desempleo y Mercados Laborales en Colombia Jaime Tenjo G. Rocio Ribero M. Abril 1998 82 Reformas comerciales, márgenes de beneficio y productividad en la industria colombiana Juán Pablo Arango Orlando Gracia Gustavo Hernández Juán Mauricio Ramírez Abril 1998 83 Capital y Crecimiento Económico en un Modelo Dinámico: Una presentación de la dinámica Transicional para los casos de EEUU y Colombia Alvaro Zarta Avila Mayo 1998. 84 Determinantes de la Inversión en Colombia: Evidencia sobre el capital humano y la violencia. Clara Helena Parra Junio 1998. 85 Mujeres en sus casas: Un recuento de la población Femenina económicamente activa Piedad Urdinola Contreras Junio 1998. 86 Descomposición de la desigualdad del Ingreso laboral Urbano en Colombia: 1976-1997 Fabio Sánchez Torres Jairo Núñez Méndez Junio 1998. 87 El tamaño del Estado Colombiano Indicadores y tendencias 1976-1997 Angela Cordi Galat Junio 1998. 88 Elasticidades de sustitución de las importaciones Para la economía colombiana. Gustavo Hernández Junio 1998. 89 La tasa natural de desempleo en Colombia Martha Luz Henao Norberto Rojas Junio 1998. 90 The role of shocks in the colombian economy Ana María Menéndez Julio 1998. 91 The determinants of Human Capital Accumulation in Donald J. Robbins Colombia, with implications for Trade and Growth Theory Julio 1998. 92 Estimaciones de funciones de demanda de trabajo dinámicas para la economía colombiana, 1980-1996 Alejandro Vivas Benítez Stefano Farné Dagoberto Urbano Julio 1998. 93 Análisis de las relaciones entre violencia y equidad Alfredo Sarmiento Lida Marina Becerra Agosto 1998. ARCHIVOS DE ECONOMIA No Título Autores Fecha 94 Evaluación teórica y empírica de las exportaciones no tradicionales en Colombia Fernando Mesa Parra María Isabel Cock Angela Patricia Jiménez Agosto 1998. 95 Valoración económica del empleo doméstico femenino no remunerado, en Colombia, 1978-1993 Piedad Urdinola Contreras Agosto 1998. 96 Eficiencia en el Gasto Público de Educación. María Camila Uribe Agosto 1998. 97 El desempleo en Colombia: tasa natural, desempleo cíclico y estructural y la duración del desempleo. 1976-1998. Jairo Núñez M. Raquel Bernal S. Septiembre 1998. 98 Productividad y retornos sociales del Capital humano: Microfundamentos y evidencia para Colombia. Francisco A. González R. Carolina Guzmán R. Angela L. Pachón G. Noviembre 1998. 99 Reglas monetarias en Colombia y Chile Jorge E. Restrepo L. Enero 1999. 100 Inflation Target Zone: The Case of Colombia 1973-1994 Jorge E. Restrepo L. Febrero 1999. 101 ¿ Es creíble la Política Cambiaria en Colombia? Carolina Hoyos V. Marzo 1999. 102 La Curva de Phillips, la Crítica de Lucas y la persistencia de la inflación en Colombia Javier A.Birchenall Abril 1999. 103 Un modelo macroeconométrico para la economía Colombiana Javier A.Birchenall Juan Daniel Oviedo Abril 1999. 104 Una revisión de la literatura teórica y la experiencia Internacional en regulación Marcela Eslava Mejía Abril 1999. 105 El transporte terrestre de carga en Colombia Documento para el Taller de Regulación. Marcela Eslava Mejía Abril 1999. Eleonora Lozano Rodríguez 106 Notas de Economía Monetaria. (Primera Parte) Juan Carlos Echeverry G. Abril 1999. 107 Ejercicios de Causalidad y Exogeneidad para Ingresos salariales nominales públicos y privados Colombianos (1976-1997). Mauricio Bussolo Orlando Gracia Camilo Zea Mayo 1999. 108 Real Exchange Rate Swings and Export Behavior: Explaining the Robustness of Chilean Exports. Felipe Illanes Mayo 1999. 109 Segregación laboral en las 7 principales ciudades del país. Piedad Urdinola Mayo 1999. 110 Estimaciones trimestrales de la línea de pobreza y sus relaciones con el desempeño macroeconómico Colombiano. (1977-1997) Jairo Núñez Méndez Fabio José Sánchez T. Mayo 1999 111 Costos de la corrupción en Colombia. Marta Elena Badel Mayo 1999 ARCHIVOS DE ECONOMIA No Título Autores Fecha 112 Relevancia de la dinámica transicional para el crecimiento de largo plazo: Efectos sobre las tasas de interés real, la productividad marginal y la estructura de la producción para los casos de EEUU y Colombia.. Alvaro Zarta Junio 1999 113 La recesión actual en Colombia: Flujos, Balances y Política anticíclica Juan Carlos Echeverry Junio 1999 114 Monetary Rules in a Small Open Economy Jorge E. Restrepo L. Junio 1999 115 El Balance del Sector Público y la Sostenibilidad Fiscal en Colombia Juan Carlos Echeverry Gabriel Piraquive Natalia Salazar Ma. Victoria Angulo Gustavo Hernández Cielo Ma. Numpaque Israel Fainboim Carlos Jorge Rodriguez Junio 1999 116 Crisis y recuperación de las Finanzas Públicas. Lecciones de América Latina para el caso colombiano. Marcela Eslava Mejía Julio 1999 117 Complementariedades Factoriales y Cambio Técnico en la Industria Colombiana. Gustavo Hernández Juan Mauricio Ramírez Julio 1999 118 ¿Hay un estancamiento en la oferta de crédito? Juan Carlos Echeverry Natalia Salazar Julio 1999 119 Income distribution and macroeconomics in Colombia. Javier A. Birchenall J. Julio 1999. 120 Transporte carretero de carga. Taller de regulación. DNP-UMACRO. Informe final. Juan Carlos Echeverry G. Agosto 1999. Marcela Eslava Mejía Eleonora Lozano Rodriguez 121 ¿ Se cumplen las verdades nacionales a nivel regional? Primera aproximación a la construcción de matrices de contabilidad social regionales en Colombia. Nelly.Angela Cordi Galat Agosto 1999. 122 El capital social en Colombia. La medición nacional con el BARCAS Separata N° 1 de 5 John SUDARSKY Octubre 1999. 123 El capital social en Colombia. La medición nacional con el BARCAS Separata N° 2 de 5 John SUDARSKY Octubre 1999. 124 El capital social en Colombia. La medición nacional con el BARCAS Separata N° 3 de 5 John SUDARSKY Octubre 1999. 125 El capital social en Colombia. La medición nacional con el BARCAS Separata N° 4 de 5 John SUDARSKY Octubre 1999. ARCHIVOS DE ECONOMIA No Título Autores Fecha 126 El capital social en Colombia. La medición nacional con el BARCAS Separata N° 5 de 5 John SUDARSKY Octubre 1999. 127 The Liquidity Effect in Colombia Jorge E. Restrepo Noviembre 1999. 128 Upac: Evolución y crisis de un modelo de desarrollo. Juan C Echeverry Orlando Gracia B. Piedad Urdinola Diciembre 1999. 129 Confronting fiscal imbalances via intertemporal Economics, politics and justice: the case of Colombia Juan C Echeverry Verónica Navas-Ospina Diciembre 1999. 130 La tasa de interés en la coyuntura reciente en Colombia. Jorge Enrique Restrepo Edgar Trujillo Ciro Diciembre 1999. 131 Los ciclos económicos en Colombia. Evidencia Empírica (1977-1998) Jorge Enrique Restrepo José Daniel Reyes Peña Enero 2000. 132 Colombia'natural trade partners and its bilateral Trade performance: Evidence from 1960 to 1996 Hernán Eduardo Vallejo Enero 2000. 133 Los derechos constitucionales de prestación y sus Implicaciones económico- políticas. Los casos del derecho a la salud y de los derechos de los reclusos Luis Carlos Sotelo Febrero 2000. 134 La reactivación productiva del sector privado colombiano Luis Alberto Zuleta (Documento elaborado para el BID) Marzo 2000. 135 Geography and Economic Development: A Municipal Approach for Colombia. Fabio José Sánchez T. Jairo Núñez Méndez Marzo 2000. 136 La evaluación de resultados en la modernización del Estado en América Latina. Restricciones y Estrategia para su desarrollo. Eduardo Wiesner Durán Abril 2000. 137 La regulación de precios del transporte de carga por Carretera en Colombia. Marcela Eslava Mejía Abril 2000. 138 El conflicto armado en Colombia. Una aproximación a la teoría de juegos. Yuri Gorbaneff Flavio Jácome Julio 2000. 139 Determinación del consumo básico de agua potable subsidiable en Colombia. Juan Carlos Junca Salas Noviembre 2000. Incidencia fiscal de los incentivos tributarios Juan Ricardo Ortega Noviembre 2000. Gabriel Armando Piraquive Gustavo Adolfo Hernández Carolina Soto Losada Sergio Iván Prada Juan Mauricio Ramirez . 140 ARCHIVOS DE ECONOMIA No Título Autores Fecha 141 Exenciones tributarias: Costo fiscal y análisis de incidencia Gustavo A. Hernández Carolina Soto Losada Sergio Iván Prada Juan Mauricio Ramirez Diciembre 2000 142 La contabilidad del crecimiento, las dinámicas transicionales y el largo plazo: Una comparación internacional de 46 países y una presentación de casos de economías tipo: EEUU, Corea del Sur y Colombia. Alvaro Zarta Avila Febrero 2001 143 ¿Nos parecemos al resto del mundo? El Conflicto colombiano en el contexto internacional. Juan Carlos Echeverry G. Natalia Salazar Ferro Verónica Navas Ospina Febrero 2001 144 Inconstitucionalidad del Plan Nacional de Desarrollo: causas, efectos y alternativas. Luis Edmundo Suárez S. Diego Mauricio Avila A. Marzo 2001 145 La afiliación a la salud y los efectos redistributivos de los subsidios a la demanda. Hernando Moreno G. Abril 2001 146 La participación laboral: ¿qué ha pasado y qué podemos esperar? Mauricio Santamaría S. Norberto Rojas Delgadillo Abril 2001 147 Análisis de las importaciones agropecuarias en la década de los Noventa. Gustavo Hernández Juan Ricardo Perilla Mayo 2001 148 Impacto económico del programa de Desarrollo alternativo del Plan Colombia Gustavo A. Hernández Sergio Iván Prada Juan Mauricio Ramírez Mayo 2001 149 Análisis de la presupuestación de la inversión de la Nación. Ulpiano Ayala Oramas Mayo 2001 150 DNPENSION: Un modelo de simulación para estimar el costo fiscal del sistema pensional colombiano. Juan Carlos Parra Osorio Mayo 2001 151 La oferta de combustible de Venezuela en la frontera con Colombia: una aproximación a su cuantificación Hernando Moreno G. Junio 2001 152 Shocks fiscales y términos de intercambio en el caso colombiano. Ómer ÖZAK MUñOZ. Julio 2001 153 Demanda por importaciones en Colombia: Una estimación. Igor Esteban Zuccardi Julio 2001 154 Elementos para mejorar la adaptabilidad del mercado laboral colombiano. Mauricio Santa María S. Norberto Rojas Delgadillo Agosto 2001 155 ¿Qué tan poderosas son las aerolíneas colombianas? Estimación de poder de mercado de las rutas colombianas. Ximena Peña Parga Agosto 2001 ARCHIVOS DE ECONOMIA No Título Autores Fecha 156 Elementos para el debate sobre una nueva reforma pensional en Colombia. Juan Carlos Echeverry Andrés Escobar Arango César Merchán Hernández Gabriel Piraquive Galeano Mauricio Santa María S. Septiembre 2001 157 Agregando votos en un sistema altamente desistitucionalizado. Francisco Gutiérrez Sanín Octubre 2001 158 Eficiencia -X en el Sector Bancario Colombiano Carlos Alberto Castro I Noviembre 2001 159 Determinantes de la calidad de la educación en Colombia. Alejandro Gaviria Jorge Hugo Barrientos Noviembre 2001 160 Evaluación de la descentralización municipal. Descentralización y macroeconomía Fabio Sánchez Torres Noviembre 2001 161 Impuestos a las transacciones: Implicaciones sobre el bienestar y el crecimiento. Rodrigo Suescún Noviembre 2001 162 Strategic Trade Policy and Exchange Rate Uncertainty Fernando Mesa Parra Noviembre 2001 163 Evaluación de la descentralización municipal en Colombia. Avances y resultados de la descentralización Política en Colombia Alberto Maldonado C. Noviembre 2001 164 Choques financieros, precios de activos y recesión en Colombia. Alejandro Badel Flórez Noviembre 2001 165 Evaluación de la descentralización municipal en Colombia. ¿Se consolidó la sostenibilidad fiscal de los municipios colombianos durante los años noventa. Juan Gonzalo Zapata Olga Lucía Acosta Adriana González Noviembre 2001 166 Evaluación de la descentralización municipal en Colombia. La descentralización en el Sector de Agua potable y Saneamiento básico. Maria Mercedes Maldonado Noviembre 2001 Gonzalo Vargas Forero 167 Evaluación de la descentralización municipal en Colombia. La relación entre corrupción y proceso de descentralización en Colombia. Edgar González Salas Diciembre 2001 168 Evaluación de la descentralización municipal en Colombia. Estudio general sobre antecedentes, diseño, avances y resultados generales del proceso de descentralización territorial en el Sector Educativo. Carmen Helena Vergara Mary Simpson Diciembre 2001 169 Evaluación de la descentralización municipal en Colombia. Componente de capacidad institucional. Edgar González Salas Diciembre 2001 170 Evaluación de la descentralización municipal en Colombia. Evaluación de la descentralización en Salud en Colombia. Iván Jaramillo Pérez Diciembre 2001 171 External Trade, Skill, Technology and the recent increase of income inequality in Colombia Mauricio Santa María S. Diciembre 2001