Diapositiva 1 - Universidad Autónoma del Estado de Hidalgo

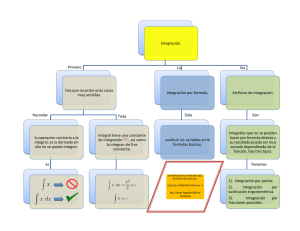
CALCULO INTEGRAL
INTEGRACION POR PARTES
Ing. Oscar Agustín Muñoz Herrerías
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
Abstract
This method is used when he made ​ordinary
can not be integrated and must be our
integral is a product of a function (u), the
derivative of another function (dv).
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
Toda regla de derivación tiene una regla
correspondiente de integración.
INTEGRACIÓN POR PARTES:
Es la regla que corresponde a la regla del producto de
derivación
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
La regla del producto expresa que si f(x) son
funciones diferentes, entonces:
En la notación de las integrales indefinidas:
Nos queda:
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
DONDE:
(u)
debe derivarse
(dv) Integrarse
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
(u) PUEDE SER LA FUNCIÓN:
A) La variable independiente
B) Cualquier función logarítmica (ln v)
C) Funciones trigonométricas inversas:
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
EJEMPLO UNO:
Sea le función: f(x)= x Sen x
f(x)= (x) (Sen x)
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
f(x)= (x) (Sen x)
y su diferencial es
Se integra:
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
Como:
Y
dv=
Se sustituye en la formula:
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
Se tiene:
Realizando operaciones:
Integrando el segundo termino:
Ordenando por signos
RESULTADO:
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
EJEMPLO DOS
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
Se deriva: (u)
Se integra a dv
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
Se tiene:
Realizando operaciones:
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
Integrando:
Factorizando:
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
OBJETIVO
Obtener una integral
más sencilla que la
inicial.
Matemático
y filósofo
alemán
Gottfried
Wilhelm
Leibniz
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
ACTIVIDAD
Resolver los siguientes ejercicios:
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4
BIBLIOGRAFIA
CALCULO DIFERENCIAL E INTEGRAL
AUTOR: JAMES STEWART
EDITORIAL: THOMSON
CALCULO DIFERENCIAL E INTEGRAL
AUTOR: GRANVILLE
EDITORIAL LIMUSA.
UNIVERSIDAD AUTONOMA DEL ESTADO DE HIDALGO
ESCUELA PREPARATORIA No. 4