soluciones y gases x
Anuncio

UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. UNIDAD III.- SOLUCIONES SUS PROPIEDADES Y ESTADOS DE LA MATERIA TEMA 1.- DEFINICIÓN DE SOLUCIÓN. COMPONENTES DE LAS DISOLUCIONES. . SOLUBILIDAD. FACTORES QUE AFECTAN LA SOLUBILIDAD. TIPOS DE SOLUCIONES. CONCENTRACIÓN DE LAS SOLUCIONES. EN UNIDADES FÍSICAS:.- % MASA/MASA .- % MASA/VOLUMEN, .- %VOLUMEN/VOLUMEN .- PARTES POR MILLÓN (PPM), UNIDADES QUÍMICAS.- MOLARIDAD NORMALIDAD. FRACCIÓN MOLAR.LEY DE DILUCIÓN TEMA 2 : GASES CONCEPTO Y PROPIEDADES.PRESION TY TEMPERATURA DE LOS GASES.LEYES QUE RIGEN EL COMPORTAMIENTO DE LOS GASES.LEY DE BOYLE, LEY DE CHARLES, LEY COMBINADA LEY DE GAY LUSSAC, LEY DE DALTON, LEY DE GRAHAM. LEY DE AVOGADRO.ECUACION D EESTADO DEL GAS IDEAL INTRODUCCIÓN: Las soluciones nos rodean por todas partes. Las bebemos, al tomar un refresco o una taza de té, las respiramos, cuando inhalamos aire, nadamos en ellas, en un océano se nada en una solución de sal en agua e incluso estamos compuestos por ellas nuestra sangre es una solución. Por ello se afirma que las soluciones son muy abundantes, puesto que no solo son la formación de una mezcla liquida sino que ellas son también los empastes de los dientes, los cálculos renales que se forman en nuestro cuerpo, el anticongelante que añaden a los vehículos en los países fríos y en fin un sin numero de soluciones con las que a diario convivimos y utilizamos, general son una mezcla de por lo menos una sustancia disuelta en otra. 1.- SOLUCIONES Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 2 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Una solución es un tipo de mezcla homogénea formada por al menos dos sustancias puras y su composición puede variar dentro de ciertos límites.(Fig 1 Y 2) Se considera que las soluciones son mezclas de un soluto y un disolvente que están unidos de forma débil. Como el soluto y el disolvente no reaccionan entre sí, pueden mezclarse en cualquier proporción. Por lo general el soluto es la sustancia presente en pequeñas cantidades, mientras el disolvente es la sustancia que se encuentra en mayor cantidad.(Fig 2) FIGURA 1 Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 3 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. El soluto se disuelve en el disolvente cualquiera que sea su estado físico; entonces se considera que el soluto es la sustancia que está siendo disuelta, mientras que el disolvente es la sustancia que está haciendo la disolución (.FIG 3 )Por ejemplo, en una solución de azúcar en agua, el azúcar es el soluto y el agua es el disolvente. Esta es una solución acuosa debido a que el disolvente es el agua. Los componentes de una solución (soluto y disolvente) se encuentran dispersos ya sea como moléculas o como iones y en muchos casos las moléculas del soluto están unidad a las del disolvente.(FIG 4) Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 4 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. En una solución acuosa de azúcar, cualquier molécula de azúcar está rodeada por moléculas de agua y se considera que está hidratada (unida por enlaces hidrógeno a las moléculas de agua). El proceso de disolver azúcar sólida en agua involucra la hidratación de las moléculas de soluto hasta que toda el azúcar se ha disuelto o hasta alcanzar cierta concentración máxima.(Fig4a) En una solución acuosa de cloruro de sodio, los dos iones, el sodio (Na1+) y el cloruro (Cl1-), se encuentran rodeados por la molécula de agua y en consecuencia están hidratados. La energía que libera durante la hidratación de iones vence las intensas fuerzas de atracción que existen entre el ion sodio (positivo) y el ion cloruro (negativo) en el cristal sólido. El ion sodio atrae el átomo de oxigeno relativamente negativo de la molécula de agua y la porción relativamente positiva hidrata al ion cloruro, como puede verse en la figura (Fig. 4 b) Algunas características de las soluciones son: a) Sus componentes no pueden separarse por métodos físicos simples como decantación, filtración, centrifugación, etc. b) Sus componentes sólo pueden separase por destilación, cristalización, cromatografía. c) Los componentes de una solución son soluto y solvente. d) En una disolución, tanto el soluto como el solvente interactúan a nivel de sus componentes más pequeños (moléculas, iones). FORMAS DE SEPARACIÓN DE LAS DISOLUCIONES Figura 5 Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 5 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. 2.- SOLUBILIDAD Si dos sustancias se disuelven el uno en el otro se dice que son miscibles, pero por el contrario si no se disuelven una en otra al mezclarse se dice que son inmiscibles. Sólo que para que esto ocurra debe cumplirse el principio “semejante disuelve a lo semejante” para ello se debe recordar que existen moléculas polares y no polares, por tanto, las sustancias polares se disolverán en sustancias polares y las no polares en sustancias no polares. Por esta razón una sustancia polar con una sustancia no polar generalmente no forma una solución. Por lo anterior podemos entender por qué la gasolina un compuesto no polar no se mezcla con el agua un compuesto polar, en cambio el agua sí se mezcla con el alcohol por que ambas son sustancias polares. Para que una sustancia se disuelva en otra es preciso: 1.- Vencer las fuerzas que mantienen unidas a las sustancias. 2.- Se deben vencer las fuerzas de atracción entre al menos algunas de las moléculas que se mezclan. 3.- Las moléculas del soluto y disolvente deben atraerse mutuamente. Para que una solución se forme el soluto debe ser soluble en un disolvente apropiado. En química, la solubilidad mide la capacidad de una determinada sustancia para disolverse en un líquido. En general se dice que la solubilidad es la proporción en que una cantidad determinada de una sustancia se disolverá en una cantidad determinada de un líquido, a una temperatura dada, o también es la facilidad con que un sólido puede mezclarse homogéneamente con el agua para proporcionar una solución química. Conceptualmente se define como: Es la mayor cantidad de soluto (gramos de sustancia) que se puede disolver en 100 gramos (g). de disolvente a una temperatura fija, para formar una disolución saturada en cierta cantidad de disolvente. Esto explica que algunos líquidos, tales como agua y alcohol, pueden ser disueltos en cualquier proporción en otro solvente. Sin embargo, el azúcar tiene un límite de solubilidad. La solubilidad depende de la temperatura; de ahí que su valor vaya siempre acompañado del de la temperatura de trabajo. En la mayor parte de los casos, la solubilidad aumenta al aumentar la temperatura. 3.- FACTORES QUE AFECTAN LA SOLUBILIDAD. a) Naturaleza del soluto y del disolvente: La disolución de las sustancias depende del tipo de sustancia o más bien del tipo de enlace que una a las mismas, dado que se hace posible la frase ”lo semejante disuelve lo semejante” por ello los compuestos iónicos (polares ) por lo general son solubles en disolventes polares y los compuestos covalentes (no polares o polares débiles ) por lo general son solubles en disolventes que no son polares. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 6 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. b) Temperatura: La solubilidad de un gas en líquido disminuye cuando aumenta la temperatura .por ejemplo, el oxígeno es soluble en agua a razón de 4.89 mL de oxígeno en 100 mL de agua a 00C; pero a 500C esta solubilidad se reduce a 2.46 mL en 100 mL de agua. La solubilidad de un sólido en un líquido por lo general aumenta cuando la temperatura se incrementa. c) Presión: Dado que los líquidos y los sólidos son casi incomprensibles, la presión tiene poco efecto sobre su solubilidad. En contraste, tiene un efecto importante en la solubilidad de los gases. La solubilidad de un gas es directamente proporcional a la presión parcial del gas sobre la solución. 4.- TIPOS DE SOLUCIONES La relación entre las masas de soluto y el disolvente así como los estados de agregación de los mismos permite establecer los tipos de soluciones las que se pueden clasificar según el siguiente esquema. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 7 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Las soluciones pueden existir en cualquiera de los tres estados físicos de la materia: Los tipos más comunes son un gas en un líquido, un líquido en un líquido y un sólido en un líquido. En tabla 1 hay algunos ejemplos de soluciones comunes. Tabla 1: Algunos ejemplos de soluciones TIPO EJEMPLO SOLUTO Soluciones Gaseosa Gas en Gas Atmósfera Oxígeno (gas) Soluciones Liquidas Agua mineral Dióxido de carbono (gas) Amoniaco Amoniaco (gas) Gas en un liquido doméstico Liquido en un Vinagre Ácido acético liquido (liquido) Sólido en un liquido Agua de mar Cloruro de sodio (sólido) Tintura de yodo Yodo (sólido) DISOLVENTE Nitrógeno (gas) Agua (liquida) Agua (liquida) Agua (liquida) Agua(liquida) Alcohol (liquido) Soluciones sólidas Liquido en un sólido Amalgama dental Mercurio (Liquido) Plata (sólido) Sólido en un sólido Bronce Cinc(sólido) Plata (sólido) Acero Carbono (sólido) Hierro (sólido) Según la cantidad de soluto podemos encontrar: SOLUCIONES SATURADAS, INSATURADAS Y SOBRESATURADAS. Solubilidad y saturación: La capacidad de una determinada cantidad de líquido para disolver una sustancia sólida no es ilimitada. En dependencia de la cantidad de soluto que se disuelva en un disolvente dado bajo ciertas condiciones de temperatura las disoluciones pueden ser: Una solución insaturada contiene menos soluto del que se puede disolver a una temperatura particular. Esto es la cantidad de soluto no se encuentra en equilibrio respecto al disolvente a una temperatura dada, ellas pueden admitir más soluto hasta alcanzar su grado de saturación Una solución saturada es aquella que contiene la máxima cantidad de soluto disuelto a cierta temperatura, o sea, que hay un equilibrio entre la cantidad de soluto y la cantidad de disolvente, y a la temperatura que se tome en consideración, el solvente no es capaz de disolver más soluto. Ejemplo 1: Manera de identificar un soluto y un disolvente Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 8 Una solución sobre saturada: Rrepresenta un tipo de disolución inestable, ya que presenta disuelto más soluto que el permitido para la temperatura dada o sea, la concentración de soluto es mayor que la de una solución saturada bajo las mismas condiciones. UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Identificar el soluto y el disolvente en cada una de las siguientes soluciones: a.1.0g de azúcar disuelto en 100 g de agua b.50 mL de agua mezclado con 20 mL de alcohol isopropílico (alcohol de frotación). c. Se prepara tintura de yodo con 1.10 g de I2 y 10.0 mL de alcohol etílico. Solución a. El azúcar esta presente en menor cantidad y se disuelve por tanto es el soluto: el agua es el disolvente. b. Como ambos el agua y el alcohol isopropílico son líquidos el que se encuentra en menor volumen, el alcohol isopropílico es el soluto. El agua es el disolvente. c. El yodo es el soluto, y el alcohol es el disolvente. CONCENTRACIÓN DE LAS SOLUCIONES Pues bien, la solubilidad de una sustancia respecto de un disolvente determinado es la concentración que corresponde al estado de saturación a una temperatura dada, por ello las propiedades de las soluciones dependen de la calidad y de la cantidad de soluto y de disolvente Dado que las soluciones son mezclas sus componentes pueden presentarse en diferentes proporciones, a cada proporción de soluto presente en determinada cantidad de disolvente la llamamos concentración, la que es la relación cuantitativa entre los componentes de la solución. Ya sabemos que la concentración de las soluciones es la cantidad de soluto contenido en una cantidad determinada de solvente. También debemos aclarar que los términos diluidas o concentradas expresan concentraciones relativas. Las unidades de concentración en que se expresa una solución o disolución pueden clasificarse en unidades físicas y en unidades químicas. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 9 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. CONCENTRACION DE LAS SOLUCIONES UNIDADES QUIMICAS UNIDADES FISICAS Molaridad Concentración en porcentaje o concentraciòn porcentual en masa y volumen Normalidad Partes por millòn Fracciòn molar Partes por billòn Diluciòn molalidad Cada método tiene una ventaja sobre los demás dependiendo de uso que se le vaya a dar a la solución. Por ejemplo si usted quiere saber sobre la masa de sal que hay en cierta masa de agua del océano, es más conveniente expresar la concentración en porcentaje referido a la masa. CONCENTRACIÓN PORCENTUAL: EXPRESA LA RELACIÓN ENTRE LA CANTIDAD DE SOLUTO POR CADA 100 UNIDADES DE DISOLUCIÓN. 1.- Relación porcentual peso / peso. (p/p) o masa – masa (m/m) Expresa la relación entre la masa de soluto con 100 partes de disolución. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 10 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Significado de una disolución en forma de porcentaje en peso o porcentaje en masa: Por ejemplo una solución de KCl al 5% significa que la solución se ha preparado: 5 gramos de KCl hay por cada en 100 g disolución. Así mismo como la disolución está compuesta por soluto y disolvente si hay 5 gramos de soluto significa que del disolvente hay 95 g. 100 g de disolución = 5 gramos de KCl + 95 g de disolvente. 2.- Relación porcentual volumen / volumen (v/v). Expresa la relación entre el volumen de soluto con 100 partes del volumen de disolución. Como los volúmenes de los líquidos o gases pueden medirse con facilidad, sus concentraciones en solución se expresan mediante el porcentaje del volumen. Significado de la relación porcentaje volumen – volumen Por ejemplo si se dice disolución de alcohol etílico al 15 % en volumen – volumen indica que la solución contiene 15 mL de soluto en cada 100 mL de solución y por tanto: habrá 85 mL de disolvente. 3.- Porcentaje peso / volumen.(p/v) Expresa la relación entre la masa de soluto con el volumen de disolución. Significado de la relación porcentaje masa – volumen Por ejemplo en una disolución de glucosa al 5% m/v, se entiende que hay 5 gramos de glucosa por cada 100 mL de disolución. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 11 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. En las ciencias de la salud, el porcentaje peso / volumen ( p/v) es empleado con frecuencia. La cantidad de soluto, se expresa en gramos y cantidad de solución en mililitros. En este porcentaje las unidades (g/mL) no se cancelan en realidad. Sin embargo el porcentaje peso / volumen generalmente se emplea para soluciones diluidas, de manera que 100 mL de solución tienen esencialmente la misma masa que 100g de agua. Para resolver problemas en que se requiera emplear la concentración porcentual como factor de conversión. Por ejemplo, se ha dicho que una solución de 5% de (p/v) de glucosa contiene 5% de glucosa por cada 100mL de solución. Esta relación se describe mediante los siguientes factores de conversión porcentuales: 5g glucosa -----------------100mL solución y 100mL solución ------------------5g glucosa Por tanto se aplicará la relación general: Procedimiento para preparar una disolución expresada en porcentaje. Por ejemplo: La solución acuosa de sulfato de sodio (NaCl) al 5% referido a la masa, se pesa la cantidad indicada de soluto en este caso es de 5.0 g dado que la solución esta al 5.0 %, luego se mide la cantidad de disolvente el que para esta corresponde a 95 g de agua. Seguidamente se procede a preparar la disolución mezclando soluto y disolvente. Figura 6 Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 12 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Ejemplo 1.-Calcule el porcentaje de azúcar en un jarabe que se prepara disolviendo 19 gramos de este en 175 g de disolución SOLUCIÓN Ya que la masa total de la solución es 175g, obtenemos con facilidad el porcentaje de azúcar Sustituyendo los datos dados: Masa de soluto % m/m = ------------------------ x 100 Masa de Disolución 19.0g azúcar %m/m = ----------------------------- x 100 = 10.9 % azúcar 175 g de disolución Significa: 10.9 partes de azúcar por 100 partes de disolución. Ejemplo 2.- Cuántos gramos de una sustancia química se necesitan para preparar 200g de una solución al 10% SOLUCIÓN 10 % de la solución significa que hay 10 g de la sustancia soluto por cada 100 g de solución, con ese dato se pueden construir dos factores: 10.0 g soluto 100g (D) --------------- y -------------100g (D) 100 g soluto Dado que se requiere encontrar cantidad de soluto se escoge el primer factor con el que se hará la conversión de la siguiente manera: 10 g de soluto 200 g de D X ---------------------= 20 g de soluto 100 g de D Ejemplo 3. Calcule el número de gramos de agua que deben agregarse a 10.0g de fenol para preparar una solución acuosa de fenol al 2.0%. SOLUCIÓN En una solución de fenol al 2.0%, hay 2.00g de fenol con 98.0g de agua para formar 100.0g de solución. Por tanto con la relación: (2.0g de fenol = 98.0g de agua). Calcule los gramos de agua necesarios para 10.0g de fenol. 10 g fenol x 98.0g agua ----------------- = 490g agua que se necesitan para 10.0g fenol. 2.00g fenol Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 13 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. USO DEL PORCENTAJE PESO/VOLUMEN PARA CALCULAR LOS GRAMOS DE SOLUTO. Ejemplo 4: Un técnico de laboratorio desea preparar 400 mL de una solución glucosada al 5% (p/v) ¿Cuántos gramos de glucosa debe utilizar? Solución: La concentración al 5.0% (p/v) puede expresarse mediante los siguientes factores de conversión porcentuales. 5.0 g glucosa --------------y 100mL (D) 100mL (D) --- ----------5.0 g glucosa Empleando el factor que cancela los mL de disolución será: 5g glucosa 400 mL de solución x ------------------------- = 20g glucosa 100 mL solución USO DEL PORCENTAJE PESO / VOLUMEN PARA CALCULAR EL VOLUMEN QUE SE REQUIERE. Ejemplo 5 El doctor Salamanca recomienda a su enfermera suministrar a un paciente 50g de lípidos empleando una solución al 10% (p/v). ¿ Cuántos mililitros debe administrarle?. Solución: La concentración al 10% (p/v) puede expresarse mediante los siguientes factores de conversión porcentuales. 10g lípidos y 100mL ------------------------100mL 10g lípidos Empleando el factor que cancela los gramos de lípidos (g lípidos ), se calcula el volumen requerido 100mL 50 g lípidos x ----------------- = 500mL solución de lípidos 10g lípidos Como prepararía 480 mL de una disolución de un antiséptico al 2.5 % p/v SOLUCION: En este caso corresponde encontrar la cantidad de soluto para preparar la disolución. La concentración 2.5 % significa que la disolución contiene 2.5 g de antiséptico por cada 100 mL de disolución. Por lo que resolvemos de la siguiente forma: Cantidad de antiséptico = 2.5 g de antiséptico 480 mL de (D) X----------------------------=12 g de antiséptico 100mL de (D) Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 14 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. 4.- PARTES POR MILLON La concentración de las soluciones muy diluidas suele expresarse en partes por millón (ppm) o incluso en partes por billón (ppb). Estas unidades son de uso frecuente para expresar niveles extremadamente bajos de sustancias tóxicas o para soluciones de uso biológico, se usan en la medicina forense, en la farmacología, industria farmacéutica, en la antropología, y en determinación de los elementos pesados que se encuentran en el aire, suelo y agua. Las unidades de masa del soluto y del disolvente deben ser las mismas. Se expresa: Esta concentración significa que hay una parte en un millón de partes. Por ejemplo según la unidad elegida puede ser un gramo en un millón de gramos, una gota en un millón de gotas, 1 mL en un millón de mL. Si analizamos la relación que hay entre los prefijos de las unidades en que se expresa la cantidad de soluto y el total de disolución y ésta es de 106, hablamos de ppm. Ejemplo: µg /g 6 Relaciones: 10 µicro ≡ 1 unidad 1microgramo / gramo = 1 ppm mg/Kg : 1mg/Kg = 1ppm = 106 mili ≡ 1 kilo mg/L : 106 miligramos ≡ 1 L (para disoluciones acuosas) 1ppb = 1 µg/L (microgramo / litro) a) Si la concentración de ozono en el aire sobrepasa las 0.11ppm ya está fuera de lo saludablemente recomendado. b) Si estás por más de una hora en un lugar cerrado que tiene una concentración de más de 0.0013% de bióxido de carbono, te empieza a doler la cabeza. c) El agua que contenga más de 0.02% de sodio no es potable, o lo que es igual más de 200 ppm. c) Si aplicamos partes por billón se expresa: Compilado por Lic. Elvis María Jiménez Peralta 15 Masa del soluto Servicio BAC 2016 Partes por billón (ppb) = --------------------- x Masa de solución 2 000 000 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Para convertir de ppm a ppb se aplica la relaciòn 1ppm = 1000 ppb Ejemplo 7. Una muestra de agua contiene 3.5 mg de iones fluoruro (F-) en 825 mL. Calcule las partes por millón (ppm) del ión fluoruro en la muestra.( Suponga que la densidad de la solución diluida de agua es 1.00g/mL.) SOLUCIÓN 3.5mg F1 mL muestra 1g muestra ppm= ---------------- x ----------------- x --------------- x 1 000 000 825 mL muestra 1.00g muestra 1000mg muestra = 4.2 ppm Ejemplo 8. Una muestra de agua contiene 128 mg de iones sodio (Na+) en 750mL de agua. Calcule las partes por millón (ppm) del ión sodio en la muestra.(suponga que la densidad de la solución diluida de agua es 1.00g/mL) SOLUCIÓN: 1 mL de muestra 1 g de muestra 128 mg Na+ ppm = -------------- x ---------------------- x --------------------x 1 000 000 750 mL muestra 1.0 g de muestra 1000 mg de muestra = 171 ppm Ejemplo 9.- En Estados Unidos, el límite federal de plomo en agua de la llave es de 0.015 ppm expresa en a) mg/L b) ppb. SOLUCIÒN. a) La relaciòn 1ppm = 1mg/L proporciona el factor de conversión adecuado multiplicando la cantidad conocida (0.015 ppm) por el factor de conversión. 1mg/L 0.015 ppm X --------- = 0.015 mg/L 1ppm b) La conversiòn a ppb se hace con base a la relaciòn 1ppm = 1000ppb 1000 ppb 0.015 ppm X --------------- = 15 ppb 1ppm Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 16 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. 3.5.2.- CONCENTRACIONES EN UNIDADES QUIMICAS. Este tipo de expresión de la concentración de una disolución tiene que ver con la cantidad de sustancia que interviene en ellas, esto es se toma en cuanta la formula de la sustancia por tanto interviene la masa de las mismas. 5.- MOLARIDAD: Expresa la relación entre el número de moles de soluto por litros de disolución La molaridad de una solución es una expresión de concentración importante desde el punto de vista químico. Expresa los moles contenidos en cada litro de disolución. Por ejemplo, para preparar un litro de una solución acuosa uno molar (1.0 M) de sulfato de sodio, (Na2SO4), se pesa la masa que representa un mol del sulfato de sodio (142.1 g) se coloca en el matraz y luego se adiciona suficiente agua completar el volumen de la solución hasta un litro, como se muestra en la figura 7. Figura 7: solución acuosa del sulfato de sodio (Na2SO4) uno molar (1.00 M). Un punto importante que se debe hacer notar aquí es que no contamos con información acerca de la cantidad de disolvente que se adiciona, solo hasta que la solución se ha llevado al volumen total de un litro. La cantidad de agua utilizada la podemos calcular si conocemos la densidad de la solución. Tabla 4.- Algunos ejemplos del significado de soluciones molares. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 17 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Molaridad En unidades Significado 1 mol HCl 1 L solución 1 mol de HCl por litro solución 2.M CaCl2 2.0 moles CaCl2 1 L solución 2.0 moles de CaCl2 por litro de solución 3.5 M KCl 3.5 moles KCl 1 L solución 3.5 moles de KCl por litro de solución 6.0 moles Na2CO3 1 L solución 6.0 moles de Na2CO3 por litro de solución 1. M HCl 6.0 M Na2CO3 CALCULO DE LA MOLARIDAD DE UNA SOLUCION Ejemplo 10 .- ¿Cuál es la molaridad (M) de cada una de las siguientes soluciones? a.- 2.0 moles de cloruro de calcio (CaCl2) en 500 mL de solución. b.- 60.0g de NaOH en 0.250 L de solución SOLUCIÓN: En el caso de la solución (a) se requiere preparar una solución de la cual el volumen está dado en mL y el volumen para encontrar la molaridad se expresa en litros, entonces será preciso transformar de mililitros a litros de la siguiente manera: 1L Es el factor de conversión 500 mL x ------------------que se construye de la 1 000 mL relación: 1L ====1000mL = 0. 5 L solución Empleando el número de moles de soluto y el volumen en litros de la solución, se calcula la molaridad como sigue: Moles CaCl2 2.0 moles CaCl2 Molaridad (m) = ------------------- = --------------------- = 4 M (se lee cuatro molar) Litros de solución 0.5 L de solución b.- .Dado que para calcular la molaridad se requiere las moles del soluto, los gramos de NaOH se convierten a moles usando la masa molar del NaOH como factor de conversión. Dato. M (NaOH) = 40 g/mol (1mol de NaOH ===== 40 g de NaOH) 60.0g NaOH 1 mol NaOH x ------------------------ = 1.50 moles de NaOH 40.0g NaOH Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 18 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Ahora con las moles de NaOH y el volumen de la solución en litros se calcula la molaridad de la solución. 1.5 moles de NaOH M = ----------------------------- = 6.00 M = 6 mol / l (seis moles / Lde solución) 0.250 L USO DE LA MOLARIDAD PARA CALCULAR LOS GRAMOS DE SOLUTO. Ejemplo 11.- ¿Cuántos gramos de KCl se necesitan pesar para preparar 0.250 L de una solución de 2.00 M de KCl? SOLUCIÓN El número de moles de KCl se determina empleando el volumen conocido de solución y molaridad como factor de conversión. La solución 2.0 molar significa 2 moles por 1 litro de solución con ello se construye el factor de conversión 2.00 moles KCl 0.250 L solución x ------------------------- = 0.500 mol de KCl 1 L solución Volumen conocido Molaridad como factor Luego se calcula la masa de soluto requerida para ello se usa la masa molar del KCl como factor de conversión.( mol de KCl ===== 74.5 g de KCl) 74.5 g de KCl 0.5 moles de KCl x ----------------------- = 37.25 g de KCl 1 mol de KCl También se puede resolver directamente despejando la formula de molaridad. Moles de soluto masa de soluto M = --------------------------- y moles de soluto = --------------------L de disolución Masa Molar Si se sustituye la formula de moles en la de molaridad resulta: Masa de soluto ------------------------------Masa molar de soluto M = ------------------------------------- L de disolución de allí se obtiene: Número de moles Masa de soluto M x L( D) = -------------------Masa molar de soluto Finalmente despejando la masa de soluto se obtiene: Masa de soluto = M x (mol/L) x g L( D) x Masa molar de soluto L x ( g/ mol) se eliminan L y moles y queda Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 19 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. (2.0mol/L) x (0.250L) x 74.5 g/mol) = 37.25 g de KCl CÁLCULO DEL VOLUMEN DE UNA SOLUCIÓN MOLAR EJEMPLO 12.- ¿Qué volumen en litros de solución 1.5 M de HCl se necesita para aportar 6.0 moles de HCl? SOLUCIÓN Empleando la molaridad como factor de conversión., con la relación 1.5 moles por 1 L de solución Se plantea el siguiente cálculo. 6.0 moles HCl 1 L solución x ----------------------- = 4.0 L de HCl 1.5 moles HCl USO DE LA MOLARIDAD PARA CALCULAR LOS MOLES DE SOLUTO Ejemplo 13 ¿Cuántas moles de NaCl se encuentran presente en 4.0 L de una solución de 2.0 M de NaCl? SOLUCIÓN: Empleando la molaridad de la solución como factor de conversión, se calcula el número de moles de NaCl.( 2.0 M indica 2.0 mol ==== 1 L de solución) 2.0 moles NaCl --------------------- = 8.0 moles de NaCl 4.0 L de solución x 1 L solución 6.- NORMALIDAD La normalidad (se abrevia N) es la cantidad de moles equivalentes (eq) de soluto por litro de solución: La masa equivalente en gramos (un equivalente) del soluto se basa en la reacción de la cual participa el soluto y está definida ya sea por el concepto ácido – base o por el concepto de oxidación – reducción, lo cual depende del uso final de la solución. Sin embargo, vamos a limitar nuestra explicación sobre los equivalentes y la normalidad a las explicaciones en donde se utiliza el concepto de equivalencia ácido – base. Definiremos entonces el término de equivalente para un acido y para una base. Un equivalente de cualquier ácido es igual a la masa en gramos de ácido capaz de proporcionar 6.02 x 1023 (número de Avogadro)) iones hidrogeno (1 mol). Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 20 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. La masa equivalente en gramos (un equivalente) de un ácido se determina dividiendo la masa molar del ácido entre la cantidad de moles de Ion hidrógeno por mol de ácido utilizado en una reacción. Un equivalente de cualquier base es igual a la masa en gramos de la base que puede combinarse con 6.02 x 1023 iones oxidrilo (1 mol). Un equivalente de una base se calcula dividiendo la masa molar de la base entre el número de iones oxidrilos que reaccionan por mol de base. . Así, un equivalente de cualquier ácido se combinará exactamente con un equivalente de cualquier base. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 21 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Un equivalente de una sal de define por medio de la reacción en que participa la sal y es igual a la masa en gramos de la sal capaz de liberar 6.02 x 1023 cargas positivas o 6.02 x 1023 cargas negativas en la reacción. El equivalente masa en gramos (un equivalente) de una sal se determina dividiendo la masa molar de la sal entre la cantidad de moles de cargas positivas o negativas por mol de sal utilizada en la reacción. En todos los casos debe tomarse en cuenta la reacción. Para preparar una solución acuosa uno Normal de sulfato de sodio, se pesa un equivalente (142.1g / 2 = 71.0g) se coloca en un matraz y se adiciona suficiente agua para llevar el volumen de la solución a un litro en un matraz volumétrico, como se muestra en la figura 8 Fig. 8.- La solución acuosa de sulfato de sodio (Na2SO4) uno normal (1.00 N) EJEMPLO 14 Calcule la normalidad de una solución acuosa de ácido fosfórico que contiene 275g de H3PO4 en 1.20 L de solución y que se utiliza en reacciones en las cuales se reemplazan los tres hidrógenos. SOLUCIÓN La masa de fórmula gramo del H3PO4 es 98.0g y como se utilizan 3 mol de iones hidrógenos por mol de ácido, por tanto un equivalente de acido fosfórico será: 98.0g/mol 1 eq de H3PO4 = --------------- = 32.6 Eq.g/mol de H3PO4 3 Eq Luego se calcula los moles equivalentes dividiendo la masa dada de soluto entre un equivalente del mismo. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 22 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Masa de soluto Moles eq. = ---------------------1 Equivalente Para el problema dado: 275g H3PO4 Moles Eq = --------------------------------- = 8.59 mol .Eq de H3PO4 32.7Eq- g mol de H3PO4 Luego se aplica la fórmula de la normalidad con los datos necesarios. 8.41 mol –eq. N = ------------------------- = 7.0 N (se lee siete normal) 1.2 L (D) La concentración obtenida significa que la solución Siete moles equivalente por litros de solución. Ejemplo 15.Cuántos gramos de Ca (OH)2 hay en 50 mL de una solución 3.0 N SOLUCIÓN: Para resolver este tipo de problemas se sigue el siguiente procedimiento: 1.- La fórmula de normalidad de despeja en función del los moles equivalentes. Moles Eq. N = -------------------------- despejando moles Eq. = (N) (L de solución) L de solución El problema da en mL el volumen entonces se convierte a litros. 1L 50mL x ---------------- = 0.05 L 1000mL Entonces de los datos obtendremos: moles Eq. = (N) (L de solución) = (3.0 moles Eq/) (0 .0 5 ) = 0.15 Eq. De Ca (OH)2 2.- Se encuentra un equivalente del Ca (OH)2 Masa molar 1Eq de Ca (OH)2 = ---------------------Numero de OH- Recordemos que el número equivalente de una base corresponde al numero de iones OH sustituibles en el caso de Ca(OH)2 tiene 2 OH- 74.1 g 1Eq de Ca (OH)2 = ------------------ = 37.1 g- Eq. 2 Eq. Con este dato usado como factor de conversión (1Eq—g de Ca(OH)2 ===== 37.1 g) se convierten los equivalentes encontrados en el paso 1 a gramos Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 23 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. 37.1g de Ca(OH)2 0.15 Eq de Ca (OH)2 x ---------------------------- = 5.6 g de Ca(OH)2 1 Eq de Ca(OH)2 EJEMPLO 16 Calcule los mililitros de una solución acuosa 2.00 N ácido sulfúrico que se necesitan para tener 120g de H2SO4 que se utilizarán en reacciones en las que se reemplazan ambos iones hidrógeno. SOLUCIÓN: Una solución de H2SO4 2.0 N contiene 2.00 eq /L de solución debido a que se usan 2 mol de iones hidrógeno por mol de ácido. 98 g 1Eq de H2SO4 = --------------- = 49.0g -Eq 2 Eq. Aplicando cada una de estas cantidades como factor de conversión tendremos: 1000 mL solución 1 eq H2SO4 1L solución 120g H2SO4 x ----------------- x ---------------- x ---------------------- =1220 mL 2 eq H2SO4 1 L solución 49g H2SO4 ADVERTENCIA Siempre agregue ácido al agua, nunca lo haga al revés. En el caso de H2SO4, agregar agua al ácido concentrado hará que éste reaccione violentamente. Por tanto en el problema que se acaba de resolver lo conveniente sería verter parte del agua en el matraz antes de agregar el H2SO4 y luego adicionar mas agua hasta la marca de aforo 7. MOLALIDAD. En primer lugar debemos advertir que molalidad no es lo mismo que Molaridad por lo cual debemos evitar confundirlas puesto que el nombre es muy parecido pero en realidad cambian mucho los cálculos, y es un grave error pero muy frecuente. En la molalidad relacionamos la molaridad del soluto con el que estamos trabajando con la masa del disolvente (en kg) que utilizamos. La definición de molalidad es la siguiente: Relación entre el número de moles de soluto por kilogramos de disolvente (m) Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 24 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Ejemplo 17.- Calcule la molalidad de las siguientes soluciones. a) 36 g de glucosa (C6H12O6) disuelta en 500 g de agua b) 0.2 moles de amoniaco disueltos en 0.3 kg de agua. SOLUCIÓN 1.- Los g de glucosa se deben convertir a moles para ello se usa la masa molar de la glucosa como factor de conversión. M(C6H12O6) = 180 g/ mol ( 180 g de glucosa ====== 1 mol de glucosa) 36 g de glucosa x 1mol de glucosa --------------------- = 0.2 mol de glucosa 180 g de glucosa a.2 .- los g de disolvente convertirlos a Kg ( 1Kg ==== 1000 g) 1Kg de agua 500g de agua x ------------------------ = 05 Kg de agua 1000 g de agua a.3.- Se calcula la molalidad. Moles de soluto 0.2 moles de glucosa m = ------------------------ = ----------------------------- = 0.4 molal Kg de disolvente 0.5 kg de agua (0.4 mol de glucosa por Kg de agua) b.1 En este caso directamente se aplica la formula de molalidad. Moles de soluto 0.2 moles de NH3 m = ----------------------- = ------------------------ = 0.67 m( 0.67 moles por Kg de agua) Compilado por Lic. Elvis María Jiménez Peralta 25 Servicio BAC 2016 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Kg de disolvente 0.3 Kg de agua 8.- FRACCION MOLAR Fracción molar (Xi): Se define como la relación entre los moles de un componente (ya sea solvente o soluto) de la solución y los moles totales presentes en la solución. La suma de la fracción molar del soluto más el disolvente es igual a la unidad. Ejemplo 18.- cual es la fracción molar de los componentes de una solución que contiene 3.8 g de NaCl en 400g de agua. SOLUCION: 1.- Calcular los moles de soluto y disolvente. Masa en g Número de moles = --------------------Masa molar Masa de NaCl Moles (NaCl) = ---------------------M NaCl 3.8 g = --------------58.5 g/mol = 0.065 mol de NaCl Masa de agua 400 g de agua Moles de agua = ----------------------- = --------------------- = 22.22mol de agua M agua 18 g/mol 2.- Cálculo de fracción molar de cada componente de la disolución. Moles de soluto 0.065 moles Χsoluto = ------------------------- = -------------------------------------------------------------Moles de disolución 0.065 moles NaCl + 22.22moles de Agua Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 26 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. 0.065 moles 0.065 moles = ------------------------------------------------------------- = ----------------- = 0.003 0.065 moles NaCl + 22.22moles de Agua 22,285 Χdisolvente Moles de disolvente 22.22moles de agua = ------------------------------ = ---------------------------------- = 0.997 Moles de disolución 22.285 moles de disolución 0.003 + 0.997 = 1 9.- DILUCIÓN DE SOLUCIONES Las soluciones de ácidos y bases se adquieren usualmente en tiendas de productos químicos. En beneficio de la economía, los abastecedores expenden la mayoría de estas soluciones en forma concentrada.(Esto es común como comprar sopas concentradas y agregarles agua).Los químicos tienen que saber cómo diluir soluciones concentradas a la fuerza que quiera. El proceso de dilución significa: Preparar una solución agregando disolvente a una solución más concentrada esto es, agregar más disolvente a la solución aumentando el volumen, causando disminución de la concentración. Sin embargo, la cantidad de soluto no cambia, es la misma en la solución diluida que en la muestra original. La figura 9 siguiente representa la dilución de una disolución. La disolución final se prepara extrayendo 1/8 de la disolución original (1 cm3) y diluyéndolo con agua hasta un volumen de 8 cm3. El número de puntos en los 8 cm3 de la disolución final representa el número de partículas de soluto y es el mismo que en 1 cm3 de la disolución inicial Generalmente el número de moles de una solución a partir de su concentración es: concentración X volumen, por tanto la fórmula será: Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 27 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Siendo C1 y V1 la concentración de la solución con mayor concentración o mejor la más concentrada., y C2 y V2 la concentración de la solución que se desea preparar con menor concentración o menos concentrada. Si nos referimos a soluciones molares o normales la fórmula será: M1V1 = M2V2 N1V1 = N1V1 El volumen puede expresarse en cualquier unidad conveniente .Pero las unidades usadas, tales como L o mililitros deben ser las mismas en ambos lados de la ecuación. Esta fórmula puede aplicarse cuando se resuelvan problemas de laboratorio Ejemplo 19. Cómo prepararía 2L de una solución de HCl 3M a partir de una solución 12 M Solución: Se necesita encontrar la cantidad de volumen de HCl concentrado que, cuando se diluya en agua, dará 2L de HCl 3M. M2V2 M1V1 = M2 V2 así que V1 = --------------M1 (3M) (2L) = ---------------- = 0.5 L 12M Dado que en el laboratorio generalmente se usan materiales que miden el volumen en mL entonces 0.5 L se convierten en 500mL Finalmente, para preparar la solución, se miden 500 mL de HCl concentrado (12M), se trasvasan a un matraz aforado de 2 L y se diluye con agua hasta completar el volumen deseado. Ejemplo 20.- Cómo prepararía 300 mL de una solución 0.6 N de H2SO4 a partir de una solución 36 N. SOLUCIÓN: Se necesita encontrar la cantidad de ácido sulfúrico concentrado para preparar la solución deseada, por tanto se hará: N1V1= N2V2 así que: N2V2 V1 = ------------N1 (0.6N) (300mL) = ----------------------- = 5mL 36N Por lo tanto, para hacer la solución final, mida 5mL de H2SO4 concentrado en un matraz aforado y diluya con agua hasta 300mL. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 28 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 29 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. UNIDADES FISICAS DE CONCENTRACION UNIDAD EXPRESION MATEMATICA %p/p Porcentaje peso a peso % Soluto = gramos de Soluto x 100 gramos de solución DESCRIPCION Describe la cantidad en gramos de Soluto o de solvente presentes en 100 gramos de solución. % Solvente = gramos de solvente x100 gramos de solución %p/v Porcentaje Peso a volumen %v/v Porcentaje volumen a volumen Ppm Partes por Millón % Soluto = gramos de Soluto x 100 mililitros de solución % Vol. de = mililitros de Soluto x 100 mililitros de solución ppm = miligramos de Soluto Kilogramos de solución ppm = miligramos de Soluto Litros de solución Molaridad, M M= Moles de Soluto Litro de solución M = moles Litro Normalidad N N = # de equivalentes-gramo de Soluto Litro de Solución Fracción Molar, X Xs = nA nA + nB Fracción de Soluto nB + nB Fracción de Solvente Xd = nA Molalidad, m Dilución M = # de moles Soluto m = moles Kg de Solvente Kg Solvente C1V1= C2V2 Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 Es una forma de expresar los gramos de Soluto que existen en un volumen de 100 mL de solución. Se emplea para expresar concentraciones de líquidos y expresa el volumen de un Soluto en un volumen de 100 mL de solución. Se emplea para hablar de soluciones muy diluidas y expresa las partes en gramos de un Soluto por cada millón de partes de solución. Corresponde al número de moles de Soluto por cada litro de solución. Expresa el número de equivalentesgramo de Soluto por cada litro de solución. Se denomina fracción molar al cociente entre el número de moles de un componente de una mezcla (A=soluto y B=solvente) y el número total de moles de todos los componentes. Está definida como el número de moles de Soluto por Kilogramos de solvente. Expresa la relación de una solución concentrada a una diluida 30 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. CLASE PRACTICA UNIDAD IV SOLUCIONES. TEMA: Concentración en unidades físicas y unidades químicas OBJETIVOS: Efectuar cálculos concentración de las soluciones en unidades físicas. Para la resolución de esta clase practica tome en cuenta los dos cuadros con los que se concluye el material teórico de esta unidad. I.- Identificar el soluto y el disolvente en las siguientes soluciones. a.- 10 g de NaCl y 100 g de H2O b.- 50 ml de etanol y 100 ml de agua c.- 100 g de plata y 40 g de mercurio e.- 20 L de oxígeno y 8 L de nitrógeno II.- Diga si los siguientes incisos se refieren a una solución saturada o no saturada a.- Un pedazo sólido de soluto se añade a una solución y no cambia de tamaño. b.- Un cubo de azúcar que se disuelve completamente cuando se añade una taza de café. c.- Todo el soluto se disuelve. III. Calcule el porcentaje de concentración de las siguientes soluciones. a.- (p/v) 2.0 g de sacarosa en 100 ml de b.- (m/m) 20.0 g de KCl en 150 g de Disolución c.- (p/v) 75.0 g de Na2SO4 en 0.5 L de Disolución d.- (v/V) 45 ml de fenol en 120 mL de cloroformo. e.- (v/v) 3.0 ml de acetona en 40 solución ml de solución g.- (m/m) 40.0 g de CaCl2 en 250 solución g de solución IV Calcule el número de gramos de soluto necesarios para preparar las siguientes soluciones. a.- 50.0 ml de una solución de KCl al 5.0 % (p/v) b.- 22.5 g de una solución de NaCl al 10 % en peso c.- 1.25 L de una solución de NH4Cl al 4.0 % (p/v) d.- 75 g de una solución de NaOH al 40.0 % en peso V. Calcule el número de gramos de disolución necesarios para preparar. a.- 10.0 g de HCl para una solución al 1.0 % en peso b.- 5.0 g de LiNO3 para una solución al 25 % en peso c.- 40.0 g de KOH para una solución al 10 % en peso VI. Calcular la molaridad de las siguientes soluciones. a.- 4.0 moles de KOH en 2.0 L de solución. b.- 2.0 moles de glucosa en 4.0 L de solución. c.- 0.10 moles de NaCl en 40.0 ml de solución. d.- 3.5 g de HCl en 1.0 L de solución. e.- 8.0 g de NaOH en 200 ml de solución. VII. Calcular el número de moles en las siguientes soluciones. a.- 1.0 L de solución de NaCl 3.0 M. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 31 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. b.- 5.0 L de solución de CaCl2 2.0 M. c. - 200 ml de solución de glucosa 4.0 M. d .- 500 ml de solución de sacarosa 10.0 M. VIII. Calcular el número de gramos de soluto necesarios para preparar cada una de las siguientes soluciones. a.- 1.0 L de solución de H2SO4 1.0 M. b.- 4.0 L de solución de KCl 2.0 M. c.- 500 ml de solución de NaCl 1.0 N. d.- 200 ml de solución de NaOH 6.0 N. XI. Calcule el peso equivalente de cada una de las siguientes sustancias. a.- HCl d.- CaCl2 b.- Mg(OH)2 e.- Al (OH)3 c.- H3PO4 f.- CaSO4 X. Calcule la normalidad de cada una de las siguientes soluciones. a.- 4.0 g de H2SO4 en 250 ml de solución. b.- 25.0 g de KOH en 100 ml de solución. c.- 10.0 g de K 2CO3 en 200 ml de solución. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 32 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. INTRODUCCION Las partículas que componen la materia pueden presentarse en tres estados físicos diferentes, principalmente, sólido, líquido y gaseoso. La diferencia entre los tres reside esencialmente a la agitación de las moléculas, lo cual es la expresión de su condición térmica. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 33 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Se denomina gas al estado de agregación de la materia que no tiene forma ni volumen propio. Su principal composición son moléculas no unidas, expandidas y con poca fuerza de atracción, haciendo que no tengan volumen y forma definida, provocando que este se expanda para ocupar todo el volumen del recipiente que la contiene, con respecto a los gases las fuerzas gravitatorias y de atracción entre partículas resultan insignificantes. Es considerado en algunos diccionarios como sinónimo de vapor, aunque no hay que confundir sus conceptos, ya que el término de vapor se refiere estrictamente para aquel gas que se puede condensar por presurización a temperatura constante. Los gases se expanden libremente hasta llenar el recipiente que los contiene, y su densidad es mucho menor que la de los líquidos y sólidos Dependiendo de sus contenidos de energía o de las fuerzas que actúan, la materia puede estar en un estado o en otro diferente: se ha hablado durante la historia, de un gas ideal o de un sólido cristalino perfecto, pero ambos son modelos límites ideales y, por tanto, no tienen existencia real. En los gases reales no existe un desorden total y absoluto, aunque sí un desorden más o menos grande. En un gas, las moléculas están en estado de caos y muestran poca respuesta a la gravedad. Se mueven tan rápidamente que se liberan unas de otras. Ocupan entonces un volumen mucho mayor que en los otros estados porque dejan espacios libres intermedios y están enormemente separadas unas de otras. Por eso es tan fácil comprimir un gas, lo que significa, en este caso, disminuir la distancia entre moléculas. El gas carece de forma y de volumen, porque se comprende que donde tenga espacio libre allí irán sus moléculas errantes y el gas se expandirá hasta llenar por completo cualquier recipiente. De los tres estados de la materia, en el estado gaseoso las interacciones entre sus partículas son mínimas, por lo que es en este caso donde el estudio y la interpretación de los resultados obtenidos son menos complicados. Como resultado de tales estudios se ha llegado a establecer una serie de generalizaciones empíricas que se incluye bajo la denominación de leyes de los gases, las cuales describen el comportamiento de dichas sustancias en determinadas condiciones especiales Si un gas es introducido en un recipiente cerrado, sus moléculas se moverán según las consideraciones de la teoría cinética molecular, con una velocidad que aumentará con la temperatura. El estado gaseoso es un estado disperso de la materia, es decir, que las moléculas del gas están separadas unas de otras por distancias mucho mayores del tamaño del diámetro real de las moléculas. Resuelta entonces, que el volumen ocupado por Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 34 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. el gas (V) depende de la presión (P), la temperatura (T) y de la cantidad o numero de moles ( n). Las propiedades de la materia en estado gaseoso son: Los gases poseen las siguientes propiedades únicas que los caracterizan: Compresibilidad: la capacidad de reducir su volumen ante la acción de la presión (una fuerza externa). Se adaptan a la forma y el volumen del recipiente que los contiene. Un gas, al cambiar de recipiente, se expande o se comprime, de manera que ocupa todo el volumen y toma la forma de su nuevo recipiente. Elasticidad: la habilidad de recuperar volumen ante la supresión de una presión externa. Se dejan comprimir fácilmente. Al existir espacios intermoleculares, las moléculas se pueden acercar unas a otras reduciendo su volumen, cuando aplicamos una presión Capacidad de Difusión: la expansión de un gas a través de todo el volumen de su contenedor. Se difunden fácilmente. Al no existir fuerza de atracción intermolecular entre sus partículas, los gases se esparcen en forma espontánea. Dilatabilidad: el incremento en volumen ante un aumento en temperatura. Se dilatan, la energía cinética promedio de sus moléculas es directamente proporcional a la temperatura aplicada. Variables que afectan el comportamiento de los gases 1. PRESIÓN Es la fuerza ejercida por unidad de área. En los gases esta fuerza actúa en forma uniforme sobre todas las partes del recipiente. La presión atmosférica es la fuerza ejercida por la atmósfera sobre los cuerpos que están en la superficie terrestre. Se origina del peso del aire que la forma. Mientras Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 35 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. más alto se halle un cuerpo menos aire hay por encima de él, por consiguiente la presión sobre él será menor. 2. TEMPERATURA Es una medida de la intensidad del calor, y el calor a su vez es una forma de energía que podemos medir en unidades de calorías. Cuando un cuerpo caliente se coloca en contacto con uno frío, el calor fluye del cuerpo caliente al cuerpo frío. La temperatura de un gas es proporcional a la energía cinética media de las moléculas del gas. A mayor energía cinética mayor temperatura y viceversa. La temperatura de los gases se expresa en grados kelvin. 3. CANTIDAD La cantidad de un gas se puede medir en unidades de masa, usualmente en gramos. De acuerdo con el sistema de unidades SI, la cantidad también se expresa mediante el número de moles de sustancia, esta puede calcularse dividiendo el peso del gas por su peso molecular. 4. VOLUMEN Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 36 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Es el espacio ocupado por un cuerpo. 5. DENSIDAD Es la relación que se establece entre el peso molecular en gramos de un gas y su volumen molar en litros. Condiciones estándar o normales El conjunto de presión y temperatura escogidas como estándar para especificar el volumen de un gas son 0°C ó 273°K y 760 mm de Hg; T PE o TPN en forma abreviada. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 37 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. TEORÍA CINÉTICA-MOLECULAR La teoría cinética-molecular trata de explicar el comportamiento y propiedades de los gases. Con extensiones apropiadas es aplicable a los estados líquido y sólido. Sus principales postulados son: 1. Toda la materia está formada por partículas discretas, muy pequeñas, llamadas moléculas (para los compuestos) o átomos (para elementos metálicos o gases nobles). En los gases las moléculas están relativamente alejadas entre sí. 2. Las moléculas de todas las substancias gaseosas están continuamente moviéndose a altas velocidades y en línea recta. Las moléculas diferentes tienen diferentes velocidades, pero el promedio de la energía cinética de todas las moléculas, en conjunto, es directamente proporcional a la temperatura absoluta. A la misma temperatura absoluta, la energía cinética media de las moléculas es igual en todos los gases. Los choques entre moléculas son completamente elásticos, es decir, cuando chocan entre sí o contra las paredes del recipiente, rebotan sin pérdida de energía. Esta afirmación es indispensable para explicar por qué la presión de un gas no cambia con el tiempo.(Al final de este capítulo se deduce la fórmula matemática). Los postulados anteriores permiten explicar por qué: a) Los gases ejercen tina presión. La presión se debe a los choques de las moléculas contra la pared del recipiente. Cada molécula choca y rebota sin pérdida de energía. Aunque la fuerza ejercida por una molécula es pequeña, el número de colisiones en una determinada área por segundo es muy grande. Como las moléculas están moviéndose rápidamente y en todas direcciones, ejercen la misma presión en todas partes del recipiente. b) Los gases son muy compresibles. Las moléculas de un gas están relativamente muy separadas y hay entre ellas un gran vacío. El rápido movimiento de las moléculas crea la impresión de que ocupan todo el espacio que las encierra, aunque en cualquier instante la mayor parte del espacio está vacío. La compresión junta a las moléculas, disminuyendo el espacio que las separa. Por el contrario, la disminución de la presión ejercida sobre un gas permite que las moléculas se alejen y ocupen más espacio o volumen. c) Los gases se difunden muy fácilmente. La difusión de los gases en un recipiente vacío o entre las moléculas de otro gas, se debe al rápido movimiento de las moléculas y a su capacidad de ocupar los espacios que hay entre ellas. d) La presión ejercida por un gas aumenta con la temperatura, si el volumen permanece constante. Al elevar la temperatura, se aumenta la energía cinética de las moléculas debido al incremento en su velocidad. Estas moléculas que se mueven a mayor velocidad chocan con más energía y celeridad por segundo contra las paredes del recipiente y así ejercen una presión mayor. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 38 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. e) Los gases se expanden al calentarlos si la presión permanece constantes. constantes Como se indicó en (d) una elevación de temperatura aumentará la velocidad de las moléculas. Si el volumen permanece constante, la presión deberá aumentar debido a la a mayor energía de las moléculas que chocan contra las paredes del recipiente. Pero como la presión se mantiene constante, es necesario dejar que el gas se expansione y así disminuye el número de colisiones contra la pared sin variar la presión. LEY DE BOYLE Esta ley nos permite relacionar la presión y el volumen de un gas cuando la temperatura es constante. La ley de Boyle (conocida también como de Boyle y Mariotte) establece que la presión de un gas en un recipiente cerrado es inversamente proporcional al volumen del recipiente, cuando la temperatura es constante,, o bien Lo cual significa que: El volumen de un gas es inversamente proporcional a la presión que se le aplica: En otras palabras: Si la presión aumenta, el volumen disminuye. Si la presión disminuye, el volumen aumenta. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 39 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Esto nos conduce a que, si la cantidad de gas y la temperatura permanecen constantes, el producto de la presión por el volumen siempre tiene el mismo valor. Matemáticamente esto es: lo cual significa que el producto de la presión por el volumen es constante. Para aclarar el concepto: Tenemos un cierto volumen de gas (V1) que se encuentra a una presión P1. Si variamos la presión a P2, el volumen de gas variará hasta un nuevo valor V2, y se cumplirá: que es otra manera de expresar la ley de Boyle. Apliquemos la fórmula en un ejemplo práctico: Ejemplo 1.- Tenemos 4 L de un gas que están a 600 mm Hg de presión. ¿Cuál será su volumen si aumentamos la presión hasta 800 mmHg? La temperatura es constante, no varía. Solución: Como los datos de presión están ambos en milímetros de mercurio (mmHg) no es necesario hacer la conversión a atmósferas (atm). Si solo uno de ellos estuviera en mmHg y el otro en atm, habría que dejar los dos en atm. Aclarado esto, sustituimos los valores en la ecuación P1V1 = P2V2. Ponemos a la izquierda el miembro con la incógnita Despejamos V2: Respuesta: Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 40 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Si aumentamos la presión hasta 800 mmHg el volumen disminuye hasta llegar a los 3 L. EJEMPLO 2. En un recipiente se tienen 30 litros de nitrógeno a 20°C y a una atmósfera de presión. ¿A qué presión es necesario someter el gas para que su volumen se reduzca a 10 litros? Primer paso: Identificar los datos que brinda el enunciado: V1= 30 L, P1= 1 atm, V2= 10 L, T= 20°C Segundo paso: Conocer la incógnita o interrogante: P2= ? Tercer paso: Identificada la interrogante, se despeja la P2 de la expresión: V1.P1 = V2.P2, quedando de la siguiente manera: P2 = P1.V1 V2 Finalmente se sustituyen los datos, y se efectúa el cálculo matemático: P2 = 1 atm . 30 L 10 L Las unidades (litros) se cancelan, quedando: P2 = 3 atm. EJEMPLO 3 ¿Cuál será el volumen final ocupado por 50 litros de oxígeno cuya presión inicial es de 560 mm de Hg y es comprimido hasta que la presión es de 2 atmósferas? La temperatura se mantiene constante durante todo el proceso. Primer paso: Identificar los datos que brinda el enunciado: V1= 50 L, P1= 560 mmHg ,P2= 2 atm ,T= cte. Segundo paso: Conocer la incógnita o interrogante: V2= ? Tercer paso: Existe una situación especial, como P2 está expresada en unidades diferentes a P1, se debe transformar una de las dos, ya sea en atm o mmHg. Por consiguiente transformaremos P2 a mmHg. P2 = 2 atm 760 mmHg = 1,520 mmHg 1 atm ·Cuarto paso: Identificada la interrogante, se despeja la V2 de la expresión: V1.P1 = V2.P2, quedando de la siguiente manera: Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 41 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. V2 = V1.P1 P2 · Finalmente se sustituyen los datos, y se efectúa el calculo matemático: V2 = 50 L . 560 mmHg 1,520 mmHg Las unidades (mmHg) se cancelan, quedando: V2 = 18,42 litros. LEY DE CHARLES Mediante esta ley relacionamos la temperatura y el volumen de un gas cuando mantenemos la presión constante. Textualmente, la ley afirma que: El volumen de un gas es directamente proporcional a la temperatura del gas. En otras palabras: Si aumenta la temperatura aplicada al gas, el volumen del gas aumenta. Si disminuye la temperatura aplicada al gas, el volumen del gas disminuye. Como lo descubrió Charles, si la cantidad de gas y la presión permanecen constantes, el cociente entre el volumen (V) y la temperatura (T) siempre tiene el mismo valor (K) (es constante). Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 42 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Matemáticamente esto se expresa en la fórmula: o cual significa que el cociente entre el volumen y la temperatura es constante. Intentemos ejemplificar: Supongamos que tenemos un cierto volumen de gas V1 que se encuentra a una temperatura T1. Si aumentamos la temperatura a T2 el volumen del gas aumentará hasta V2, y se cumplirá que: Que es otra manera de expresar la ley de Charles. Veamos un ejemplo práctico y sencillo: EJEMPLO 4. Un gas cuya temperatura llega a 25° C t iene un volumen de 2,5 L. Para experimentar, bajamos la temperatura a 10° C ¿ Cuál será su nuevo volumen? Solución: El primer paso es recordar que en todas estas fórmulas referidas a la temperatura hay que usar siempre la escala Kelvin. Por lo tanto, lo primero es expresar la temperatura en grados Kelvin: T1 = (25 + 273) K= 298 K ; T2 = (10 + 273 ) K= 283 K Ahora, sustituimos los datos en la ecuación: Ahora, despejamos V2: Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 43 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Respuesta: Si bajamos la temperatura hasta los 10º C (283º K) el nuevo volumen del gas será 2,37 L. EJEMPLO 5 A 1,5 atmósferas y 25 °C el volumen de un gas es de 600 cm3, si la presión permanece inalterable ¿Cuál será el volumen del gas a 20 °C? Primer paso: Identificar los datos que se dan en el enunciado. P1= 1,5 atm (cte),T1= 25°C ,V 1= 600 cm3 , T2= 20 °C Segundo paso: Conocer cual es la incógnita o interrogante. V2= ? Tercer paso: Despejar V2 de la expresión: V1.T2 = V2.T1, quedando así: V2= V1.T2 T1 Cuarto paso: Transformar °C a K, de la siguiente manera: T1: K= °C + 273 T2: K= °C + 273 K= 25 + 273= 298 K K= 20 + 273= 293 K Finalmente se sustituyen los valores y se realiza el cálculo matemático. V2= 600 cm3 . 293 K 298 K Se cancelan las unidades (Kelvin) y se obtiene el resultado: V2= 589,93cm3 Ejemplo 6. Se tienen 0,2 litros de un gas a 30 °C y una atmósf era de presión ¿Qué temperatura hay que aplicarle para que aumente a 0,3 litros? Primer paso: Identificar los datos que se dan en el enunciado. V1= 0,2 L,T1= 30 °C,P= 1 atm (cte), V 2= 0,3 L Segundo paso: Conocer cual es la incógnita o interrogante. T2= ? Tercer paso: Despejar T2 de la expresión: V1.T2 = V2.T1, quedando así: T2= V2.T1 V1 · Cuarto paso: Transformar °C a K, de la siguiente manera: Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 T1: K= °C + 273 44 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. K= 30 + 273= 303 K · Finalmente se sustituyen los valores y se realiza el cálculo matemático. T2= 0.3 L . 303 K 0,2 L Se cancelan las unidades (litros) y se obtiene el resultado: LEY DE GAY-LUSSAC : Esta ley establece la relación entre la presión (P) y la temperatura (T) de un gas cuando el volumen (V) se mantiene constante, y dice textualmente: La presión del gas es directamente proporcional a su temperatura. Esto significa que: Si aumentamos la temperatura, aumentará la presión. Si disminuimos la temperatura, disminuirá la presión. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 45 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Si lo llevamos al plano matemático, esto queda demostrado con la siguiente ecuación: La cual nos indica que el cociente entre la presión y la temperatura siempre tiene el mismo valor; es decir, es constante. Llevemos esto a la práctica y supongamos que tenemos un gas, cuyo volumen (V) no varía, a una presión P1 y a una temperatura T1. Para experimentar, variamos la temperatura hasta un nuevo valor T2, entonces la presión cambiará a P2, y tendrá que cumplirse la siguiente ecuación: la cual nos indica que el cociente entre la presión y la temperatura siempre tiene el mismo valor; es decir, es constante. EJEMPLO 7 Llevemos esto a la práctica y supongamos que tenemos un gas, cuyo volumen (V) no varía, a una presión P1 de 970 mm de Hg y a una temperatura T1 de 250C. Para experimentar, variamos la temperatura hasta un nuevo valor T2, entonces la presión cambiará a P2 760 mm Hg, y tendrá que cumplirse la siguiente ecuación: Ahora despejamos T2: Respuesta: La temperatura debe bajar hasta los 233,5º Kelvin. Si convertimos estos grados en grados Celsius hacemos 233,5 − 273 = −39,5 °C. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 46 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. EJEMPLO 8 Un gas en un recipiente de 2 litros a 293 K y 560 mmHg. ¿A qué temperatura en °C llegará el gas si aumenta la pres ión interna hasta 760 mmHg? Primer paso: Identificar los datos que presenta el enunciado. V= 2 L, T1= 293 K , P1= 560 mmHg, P2= 760 mmHg Segundo paso: Conocer la incógnita o dato a calcular. T2= ? Tercer paso: Despejar T2 de la expresión P1 = P2 , quedando así: T1 T2 P2. T1 T2 = ----------------P1 · Cuarto paso: Sustituir datos y efectuar el calculo matemático. T2= 760 mmHg . 293 K 560mmHg Se cancelan las unidades (mmHg) y se obtiene el resultado: T2= 397, 76 K · Quinto paso: Se transforma la unidad (Kelvin) a °C. °C = K - 273 °C = 397,76 - 273 °C = 124,76 EJEMPLO 9¿Cuál será la presión en atmósfera de un gas a 85 °C, sabiendo que a 25°C es de 625 mmHg? Primer paso: Identificar los datos que presenta el enunciado. T1= 85°C, T 2= 25°C, P 2= 625 mmHg Segundo paso: Conocer la incognito o dato a calcular. P1= ? Tercer paso: Despejar T2 de la expresión P1 = P2 , quedando así: T1 T2 P1= P2 . T1 T2 · Cuarto paso: Transformar las unidades (°C) a Kelvin. T1: K= °C + 273 T2: K= °C + 273 K= 85 + 273= 358 K K= 25 + 273= 298 K Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 47 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. · Quinto paso: Transformar las unidades (mmHg) a atmósfera. 625 mmHg . 1 atm 760 mmHg = 0,822 atm · Sexto paso: Sustituir datos y efectuar el calculo matemático. P1= 0,822 atm . 358 K 298 K Se cancelan las unidades (K) y se obtiene el resultado: P1= 0,987 atm LEY COMBINADA DE LOS GASES La ley general de los gases o ley combinada dice que una masa de un gas ocupa un volumen que está determinado por la presión y la temperatura de dicho gas. Estudia el comportamiento de una determinada masa de gas si ninguna de esas magnitudes permanece constante. Esta ley se emplea para todos aquellos gases ideales en los que el volumen, la presión y la temperatura no son constantes. Además la masa no varía. La fórmula de dicha ley se expresa: (V1 * P1) / T1 = (V2 * P2) / T2 Es decir, el volumen de la situación inicial por la presión original sobre la temperatura es igual a el volumen final por la nueva presión aplicada sobre la temperatura modificada. La presión es una fuerza que se ejerce por la superficie del objeto y que mientras más pequeña sea ésta, mayor presión habrá A partir de la ley combinada podemos calcular la forma como cambia el volumen o presión o temperatura si se conocen las condiciones iniciales (Pi,Vi,Ti) y se conocen dos de las condiciones finales (es decir, dos de las tres cantidades Pt, Vt, Tf). "El volumen ocupado por una masa gaseosa, es inversamente Proporcional a las presiones y directamente proporcional a las temperaturas absolutas que soportan" Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 48 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. De acuerdo con el enunciado, se puede establecer la siguiente expresión matemática: P1 V1 P2 V2 --------- = ----------T1 T2 EJEMPLO10 Una masa gaseosa ocupa u volumen de 2,5 litros a 12 °C y 2 atm de presión. ¿Cuál es el volumen del gas si la temperatura aumenta a 38°C y la presión se incrementa hasta 2,5 atm? · Primer paso: identificar los datos que brinda el enunciado. V1= 2,5 L ,T1= 12 °C ,P 1= 2 atm ,T2= 38 °C , P 2= 2,5 atm ·Segundo paso: Conocer la incógnita. V2 = ? · Tercer paso: Despejar V2 de la expresión V 1 . P1 = V 2 . P2, quedando así: T1 T2 V2= V1 . P1 . T2 T 1 . P2 · Cuarto paso: Transformar las unidades de temperatura (°C) a Kelv in. T1: K= °C + 273 T2: K= °C + 273 K= 12 + 273= 285 K K= 38 + 273= 311 K · Quinto Paso: Sustituir los datos en la expresión y efectuar los cálculos matemáticos. V2 = 2,5 L . 2 atm . 311 K 285 K . 2,5 atm Se cancelan las unidades de presión y temperatura (atm y K), se obtiene el resultado. V2 = 2, 18 L LEY DE DALTON SOBRE LAS PRESIONES PARCIALES. Esta ley se usa frecuentemente para calcular la presión de un gas que ha sido recogido o almacenado por desplazamiento de agua, puesto que estos gases se saturan de agua, y la presión total de ellos es la suma de las presiones del gas y del vapor de agua a la temperatura de observación. Para obtener la presión verdadera del gas es necesario restar la presión del vapor de agua.(tabla 1) La presión total de una mezcla gaseosa es la suma de las presiones parciales de los gases que la componen Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 49 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Ptotal = P1 + P2 + P3 …..Pn Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 50 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 51 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. EJEMPLO 11. Se recogió un gas por desplazamiento de agua a 27 ºC. La presión barométrica durante la recolección fue 766.7 mm Hg. Se recogieron a esta temperatura y presión 250 ml. ¿Cuál es el volumen del gas seco en condiciones estándar? Respuesta Usando la ecuación combinada para los gases ideales se obtiene V2, volumen en condiciones estándar. V1 = 250 ml T1 = 300 ºK V2 = ? P2 = 760 mm T2 = 273 ºK Para obtener P1, la presión verdadera del gas, usamos la ley de Dalton y buscando en la Tabla 4-1 la presión de vapor del agua a 27 ºC, tenemos: P1 = Pt - PH2O = 766.7 - 26.7 = 740 mm Hg Substituyendo: V2 = 221 ml a condiciones estándar EJEMPLO 12. Una muestra de aire solo contiene nitrógeno y oxígeno gaseoso, cuyas presiones parciales son 0,80 atmósfera y 0,20 atmósfera, respectivamente. Calcula la presión total del aire. Primer paso: Identificar los datos que brinda el enunciado. P(N)= 0,80 atm P(O)= 0,20 atm · Segundo paso: Conocer la incógnita o interrogante. Ptotal=? · Tercer paso: Sustituir los datos en la expresión matemática y efectuar el calculo. Pt= P(N) + P(O) Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 52 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Pt= 0,80 atm + 0,20 atm Pt= 1 atm EJEMPLO 13. Una muestra de gases contiene CH4, C2H6 y C3H8. Si la presión total es de 1,50 atm y la fracción molar de cada gas son 0.36; 0.294; 0.341; respectivamente. Calcular las presiones parciales de los gases. Primer paso: Identificar los datos que brinda el enunciado. X(CH4)= 0,34 X(C2H6)= 0,294 X(C3H8)= 0,341 PTotal= 1,50 atm Segundo paso: Conocer la incógnita o interrogante. P (CH4)=? P (C2H6)= ? P (C3H8)= ? · Tercer paso: Sustituir los datos en la expresión matemática y efectuar los cálculos. Pparcia l= X(gas) . Ptotal P(CH4)= 0,34 . 1,50 atm= 0,51 atm P(C2H6) = (0,294)(1,50 atm) = 0,196 atm P (C3H8) = (0,341) ( 1, 50 atm) = 0,512 atm LEY DEL GAS IDEAL La ley de los gases ideales es la ecuación de estado del gas ideal, un gas hipotético formado por partículas puntuales, sin atracción ni repulsión entre ellas y cuyos choques son perfectamente elásticos (conservación de momento y energía cinética). La energía cinética es directamente proporcional a la temperatura en un gas ideal. Los gases reales que más se aproximan al comportamiento del gas ideal son los gases monoatómicos en condiciones de baja presión y alta temperatura. Empíricamente, se observan una serie de relaciones proporcionales entre la temperatura, la presión y el volumen que dan lugar a la ley de los gases ideales, deducida por primera vez por Émile Clapeyron en 1834. En 1648, el químico Jan Baptist van Helmont creó el vocablo gas, a partir del término griego kaos Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 53 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. (desorden) para definir las características del anhídrido carbónico. Esta denominación se extendió luego a todos los cuerpos gaseosos y se utiliza para designar uno de los estados de la materia. La principal característica de los gases respecto de los sólidos y los líquidos, es que no pueden verse ni tocarse, pero también se encuentran compuestos de átomos y moléculas. La causa de que un gas sea tal se encuentra en sus moléculas, que se encuentran muy separadas unas de otras y se mueven en todas las direcciones. Al igual que ocurre con los otros dos estados de la materia, el gas también puede transformarse (en líquido) si se somete a temperaturas muy bajas. A este proceso se le denomina condensación. La mayoría de los gases necesitan temperaturas muy bajas para lograr condensarse. Por ejemplo, en el caso del oxígeno la temperatura necesaria es de 183°C. "Esta ecuación establece la relación existente entre el volumen, la presión, la temperatura y una cantidad específica (en moles) de un gas" Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 54 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Con la aplicación de dicha expresión, puedes llegar a calcular presión, volumen, temperatura o el número de moles de un compuesto. A continuación puedes observar un ejemplo que demuestra su aplicación. Calcula el número de moles de un gas que se encuentra en un recipiente cerrado de 2,0 litros, sometido a una presión de 2,3 atmósferas y a 25°C. · Primer paso: Identifcar los datos que brinda el enunciado. V= 2,0 L P= 2,3 atm T= 25 °C · Segundo paso: Conocer la interrogante o incógnita. n=? · Tercer paso: Despejar (n) de la expresión matemática P . V = n . R . T, quedando así: n = P.V R.T Recuerda que el valor de R es 0, 0821 atm.L/mol.K Cuarto paso: Transformar las unidades de temperatura (°C) a Kelvin. K= °C + 273 Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 55 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. K= 25°C + 273= 298 K Cuarto paso: Sustituir los datos en la expresión matemática y efectuar el calculo. n= 2,3 atm . 2,0 L 0,0821 atm . L . 298 K mol . K Se cancelan las unidades de presión, volumen y temperatura (atm, L, K) n= 0,188 mol Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 56 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. CLASE PRACTICA 1 TEMA: LEYES DE LOS GASES LEY DE BOYLE 1.- Un cilindro de motor de automóvil con un volumen de 400 cm3 se comprime a un volumen de 100. cm3 a temperatura constante. SI la presión gaseosa inicial era de 1 atm ¿Cuál es la presión final? 2.- Un tanque contiene 500. mL de aire comprimido a 1800. torr ¿ Qué volumen ocupará el aire comprimido a 750 torr, suponiendo que la temperatura no cambia? 3.- Una muestra de gas tiene un volumen de 390 mL medido a 250C y 760 torr.¿ Qué volumen en mL ocupará a 250C y 195 torr? 4.- ¿Qué presión final en torr debe aplicarse a una muestra de gas que tiene un volumen de 190 mL a 200C y 750 torr de presión para permitir la expansión del gas a un volumen de 600 mL a 200C? LEY DE CHARLES 1.- Un globo lleno de helio tenía un volumen de 4.00 mL cuando estaba a – 1200C¿Cuál será el volumen del globo luego de calentarlo en un horno a 1000C, suponiendo que la presión no cambia?. 2 - Si una muestra de 1500.mL de aire a 220C se enfría lo suficiente para que su volumen disminuya a 750. mL a presión constante. ¿Cuál es la temperatura Celsius final que se necesita? ¿Cuál fue el cambio de temperatura? 3.-Una muestra de gas ocupa 220mL a 100C y 750 torr ¿ Qué volumen en mL ocupará el gas a 200C y 750 torr. 7.-Un gas ocupa un volumen de 120 mL a 270C¿A qué temperatura en 0C tendrá un volumen de 80.0 mL a 630 torr? LEY DE GAY LUSSAC 1.-Se arrojo dentro de un incinerador que funciona a 7500C una bombilla eléctrica con una presión interna de 720.torr a 200C¿ Qué presión interna deberá ser capaz de soportar la bombilla para que no se rompa? 2.- El aire que está dentro de un frasco e judías verdes envasadas en casa se calienta al punto de ebullición del agua (1000C), y se cierra el frasco herméticamente a esa temperatura. ¿Cuál será la presión entro del frasco cuando éste se enfrié a la temperatura ambiental de 200C? Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 57 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. 4.- Un gas ocupa un volumen de 50.0mL a 270C y 630 torr. ¿A qué temperatura en 0 C la presión sería de 770 torr si el volumen permanece constante? 8.- Una muestra de gas ocupa un volumen de 5.00L a 700 torr y 300C¿ A qué temperatura en 0C la presión sería de 620 torr si el volumen permanece constante? LEY COMBINADA DE LOS GASES 1.- ¿ Qué volumen ocuparán a TPE 25.2 mL de hidrógeno gaseoso a 210C y a una presión de 1.96. atm? 2.- ¿Qué volumen ocupará a TPE 150. mL de Neón gaseoso a 230C y 710 torr? 3.- Una muestra de gas tiene un volumen de 5.10 L a 270C y 640 mm Hg. Su volumen y temperatura cambian a 2.10 L y 10000C, respectivamente. Calcule la presión en mm Hg en estas condiciones. 4.- Un gas mide 310 mL a PTN. Calcule su presión en atmósferas si cambia el volumen a 450 mL y la temperatura a 500C. 5.-Un gas mide 150 mL a PTN .Calcule la temperatura en 0C si el volumen cambia a 320 mL y la presión a 950 torr. 6.-Un gas tiene un volumen de 125 mL a 570C y 640 torr. Calcule su temperatura en 0C si el volumen a 325 mL y la presión disminuye a 590 tor. VOLUMEN Y MOLES DE GASES (Avogadro) 1.-Si tengo una botella de 1.0 L. Llena de oxígeno gaseoso a presión y temperatura ambientales, y tengo además una botella de 2.0L Llena de oxígeno gaseoso cuántas moléculas de gas hay en la botella más grandes con base en la hipótesis de Avogadro. 2.- Si tengo una botella de 500. mL Llena de amoniaco gaseoso, y tengo además una botella de 2.00 L. Llena de oxígeno gaseoso a la misma presión y temperatura, ¿Qué es lo que puedo saber respecto a la proporción de moles de los gases de las botellas? 3.- A cierta temperatura y presión 4.12 de CO2 ocupaban un volumen de 2.37 L¿ Cuál será el volumen de 0.500 mol de CO2 en las misma condiciones?. VOLUMEN MOLAR Y DENSIDAD DE GASES 1.-¿Qué volumen ocupan 0.200 g de oxígeno gaseoso a TPE? 2.- ¿Cuántos miligramos de CO2 hay en una botella de 4.00 L. Llena de es gas de TPE? Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 58 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. 3.-¿Cuántos moles de helio pueden estar dentro de un globo que tiene un volumen de 6.00 L a TPE? 4.-¿Cuál es la densidad de nitrógeno gaseoso a TPE? 5.-¿ Cuál es la densidad de cloro gaseoso a TPE? 6.- ¿Qué presión ejercen, en atmósferas,44.0 mol de propano en un tanque de 36 L a 220C. 7.-¿Cuántos gramos de helio hay en un globo que contiene 8.50L de gas a una temperatura de 200C y a una presión de 800 torr? LEY DE DALTON DE LAS PRESIONES PARCIALES 1.-Una mezcla de gases a 200C y con un volumen de 2.00L tienen la siguiente presiones parciales para cada uno de sus componentes: oxígeno, 180 torr, Nitrógeno 320 torr, Hidrógeno, 46 torr. a) Calcule la presión en torr de la mezcla b) Calcule el volumen en Litros a PTN que ocuparían los gases que quedan a eliminar en forma selectiva el hidrógeno 2.- Una mezcla de gases a 500C y con un volumen de 450 mL tiene las siguientes presiones parciales para cada uno de sus componentes: Helio, 120 torr, Argón, 180 torr; Kriptón, 60 torr; Xenón 25 torr. a) Calcule la presión total en torr de la mezcla b) Calcule el volumen en mL a PTN que ocuparían los gases que quedan al eliminar el Kriptón en forma selectiva. 3.-El volumen de una muestra de oxígeno recolectada sobre agua es de 175 mL a 250C y 600.0 torr. Calcule el volumen del oxígeno seco en mL a PTN. 4.-El volumen de una muestra de nitrógeno recolecta sobre agua es de 245 mL a 250C y 700 torr. Calcule el volumen del nitrógeno seco a PTN. ECUACIÓN DEL GAS IDEAL 1.-Calcule el volumen en mL de 0.0250 mol de nitrógeno gaseoso a 300C y 1.10 atm 2.-Calcule la presión en atm de 16.8 g de nitrógeno gaseoso que ocupan un cilindro de 12.0l a 350C. 3.-Calcule la temperatura en 0C de 0.310 mol de nitrógeno gaseoso que ocupan un cilindro de 10.00 L a 0.95 atm. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 59 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. 4.-Calcule la cantidad de gramos de nitrógeno gaseoso (N2) que hay en un cilindro de 6.00L a 270 C y 800 torr, sugerencia convierta la presión en torr a atm) 5.-¿Cuál es la masa molecular de un gas si 485 mL medidos a 300C y 600 torr tienen una masa de 0.384 g? 6.-Un volumen de 0.972 L de un gas medido a 500 C y 700 torr tiene una masa de 0.525 g. Calcule su masa molecular. 7.-Calcule la densidad de dióxido de carbono en g/L a 350C y 3.00 atm 8.-Calcule la densidad del metano (CH4) en g/L a –450C y 300 torr 9.-Calcule los mL de gas hidrógeno a 250C y 640 torr que se producen al reaccionar 0.520 g de magnesio con un exceso de ácido clorhídrico (para completar y balancear esta ecuación 10.-Calcule la cantidad de moles de nitrato de potasio que se necesitan para producir 4.25 L de oxígeno a 300 C y 710 mm Hg y luego convierta el volumen de oxígeno gaseoso a condiciones PTN 11.-Calcule la masa molecular de un gas que tiene una densidad de 2.20 g/L a 300 C y 460 mm Hg BIBLOGRAFIA: ALAN SHERMAN, SHARON J. SHERMAN, LEONEL RUSSIKOFF. CONCEPTOS BASICOS DE QUIMICA. PRIMERA EDICION 1999.CECSA DAUB SEESE, CARRILLO, GONZALEZ, MONTAGUD, NIETO, SANSON. QUIMICA. OCTAVA EDICIÓN. KAREN C. TIMBERLAKE. QUÍMICA INTRODUCCIÓN A LA QUÍMICA GENERAL A LA ORGÁNICA Y ALA BIOQUÍMICA. QUINTA EDICIÓN. RALF A. BURN. FUNDAMENTOS DE QUIMICA. CUARTA EDICION WWW. LA MANZANADENEWTON. WWW. QUIMICA Y SOCIEDAD.ORG Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 60 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA FACULTAD DE CIENCIAS E INGENIERIAS DEPARTAMENTO DE QUÍMICA. Compilado por Lic. Elvis María Jiménez Peralta Servicio BAC 2016 61




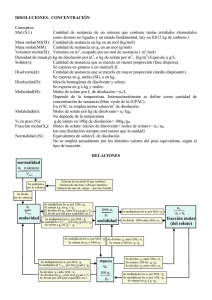

![guíasoluciones[2][1]](http://s2.studylib.es/store/data/004409996_1-4c22b608b62968c9dca601aaf9328ec2-300x300.png)


