SPLINES UN MÉTODO PARA AJUSTAR CURVAS NO LINEALES
Anuncio

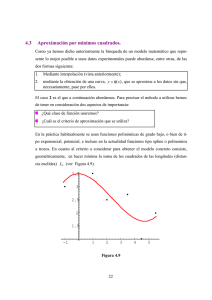
SPLINES UN MÉTODO PARA AJUSTAR CURVAS NO LINEALES IRENE SÁNCHEZ GUEVARA* INTRODUCCIÓN Uno de los problemas en economía y administración consiste en determinar el comportamiento de la variable demanda de un bien a través del tiempo o con respecto a la variable precio, con el objeto de hacer planeaciones y toma de decisiones. El planteamiento del problema es: Dada una tabla de datos x y xl y, Xn Yn Donde la variable x puede ser el tiempo o el precio de un bien y la demanda. Y una gráfica (x-y) y x Se desea obtener f(x). Profesora-investigadora del Departamento de Política y Cultura, uAM-Xochimilco. 31 Reflexiones Finisec ulares : las Matemáticas en las Ciencias Sociales ANTECEDENTES Los métodos de suavizamiento Cuando se cuenta con un conjunto de observaciones hechas cronológicamente en intervalos de tiempo fijos (a este conjunto se le denominará serie de tiempo económica), los procedimientos usuales para determinar el comportamiento de la variable demanda son: promedios móviles, suavizamiento exponencial, y Winters. La construcción de modelos con estos métodos se basa en descubrir un patrón de comportamiento de los datos en el pasado y extrapolar para hacer predicciones futuras. Los métodos de promedios móviles, suavizamiento exponencial y Winters resuelven el problema parcialmente porque solo generan otra tabla de datos en los mismos intervalos, sin embargo sus cálculos en principio son fáciles, pero lo importante es que en general van construyendo el nuevo dato por "pedazos", es decir toman un subconjunto de datos y obtiene el nuevo dato. Los promedios móviles simples toman un subconjunto de datos y obtiene el promedio para la observación posterior. Los PM dobles o lineales construyen rectas sobre un conjunto de datos y las van uniendo, lo que da un "movimiento', es decir trata de ajustar los datos a una funcional que corresponde a un conjunto de rectas. Dato calculado a partir de la recta que paso por los tres datos originales y X 32 Irene Sánchez Guevara Los de suavizamiento exponencial hacen una combinación lineal entre el dato pasado y un pronóstico pasado para obtener el dato calculado actual, para lo cual usa un parámetro (x. Y3 f3 -a- 1 2 3 f4 =ay3+(1-a)f3 4 Estos dos conjuntos de métodos son útiles cuando se trata de comportamiento constantes o con tendencia, pero si se trata de datos que además presenten estacionalidad, un método adecuado será el de Winters que además de generar las tendencias genera índices estacionarios utilizando tres parámetros. En la siguiente gráfica se muestra un ejemplo de una serie cuyos datos tienen un comportamiento claramente estacional, observe que el método winters sólo construye otro conjunto discreto de datos y no es posible tener cálculos para medidas intermedias lo cual representa una carencia importante cuando se quiere estudiar las ciclicidades. y ! _ • x Método de Winters 33 Reflexiones Finiseculares: las Matemáticas en las Ciencias Sociales Estos modelos son de prueba y error debido a que la elección de los parámetros es subjetiva, lo cual constituye otra de sus desventajas, ya que el proceso para obtener el mejor modelo consiste en proponer parámetros, calcular los errores y haces análisis de error y así la facilidad de los cálculos desaparece totalmente al convertirse en un problema combinatorio. Un esquema del proceso que se sigue en estos procesos es el siguiente: Da tos ^X1 t y T Elección del Modelo ¿Patrón de comportamiento' y Cálculos x o t 1 y 1 ¡(.r Análisis del error No ¿Aceptable? >------------------ - 34 Irene Sánchez Guevara AJUSTE POLINOMIAL Cuando lo que se quiere es obtener la relación funcional entre el precio de un bien y su demanda, una de las técnicas más utilizadas es la de mínimos cuadrados que consiste en: Dada una tabla de observaciones: X y xi Yi xn Yn Donde "x" es el precio, "y" la demanda. La gráfica es la siguiente: Se desea obtener el olinomio: Y= x p No+Nlx+fl2 Matricialmente 2 +..+Nkxk +E Y= X/3 +E 35 Reflexiones Finiseculares : las Matemáticas en las Ciencias Sociales MÍNIMOS CUADRADOS Y para obtener la estimación del vector de coeficientes R se aplica la técnica mínimos cuadrados: Mínj(y - 9¡)2 Mín = 1 e2 XXb = Xy b = (XX)-'X'y Donde: yx2 1 X= Ex] b= y= I: xK La validación del modelo recae en las pruebas de hipótesis para probar independencia y normalidad n los errores y: E(b)=,8i Además de hacer el análisis de varianza y correlación. Sin embargo, la mayor desventaja está en la inestabilidad de los cálculos de la inversa de la matriz XTX 36 Irene Sánchez Guevara Los SPLINES Para ajustar una curva a un conjunto de datos grande que no presenta un patrón de comportamiento lineal o constante, sino que presenta un patrón estacionario por ejemplo y además con tendencia exponencial, y que además deseamos tener una función continua para poder obtener datos intermedios (sobre todo cuando se estudian las ciclicidades), ya hemos visto que los métodos de suavizamiento o los de mínimos cuadrados no son muy adecuados, entonces en este trabajo hacemos la propuesta de utilizar las funciones spline. El alisamiento o suavizamiento con funciones spline reconstruye una función a partir de un conjunto discreto de datos utilizando las ideas de los métodos de suavizamiento y la técnica de mínimos cuadrados. La definición técnica de las funciones spline es: Dados los nodos (puntos) T:x1<x2<...<x„ (n_2p-1), por una función spline natural de orden 2p-1 y con nodos T, entenderemos una función de clase C2P-2 en todo R tal que: a) Es polinomial de grado no mayor que 2p-1 en [xi, xi-1], i= 1, 2 ...,n-1 b) Es polinomial de grado no mayor que p-1 en (-oo,x1) y (x,,,oo) Esta definición nos dice que por cada par de nodos se construye un polinomio de grado p-1 y que se une `lisamente" en cada nodo interior. En este trabajo utilizaremos splines naturales cúbicas, es decir, por cada par de nodos se contruye un polinomio cúbico, y en cada nodo la primera y segunda derivada coinciden, logrando una funcional suave en todo el dominio. LA TÉCNICA DE SUAVIZAMIENTO CON SPLINE CÚBICA El problema de suavizamiento constituye en encontrar una función que pueda interpolar; es decir, "pasar" por los nodos o solo seguir la tendencia de ellos y consiste en 37 Reflexiones Finiseculares: las Matemáticas en las Ciencias Sociales Donde: Hallar S, (x) tal que : Mín ^A [f] _ O, [s, feCP (a,b ) La primer parte de la funcional corresponde a los mínimos cuadrados, la segunda es la minimización del área de la curva ; es decir es la parte suavizadora y 1 es el parámetro de alisamiento, un número real y positivo que si vale cero se obtiene la función s(x) para interpolar, mientras que si tiende a infinito se obtendrá la recta mínimos cuadrados, w son los pesos que podrían corresponder a las desviaciones estándar de la variable y. 2 [f=^ f(x^)-yr 2+a J[21 (t)t rr i=1 uw1 Las condiciones del mínimo deben cumplir con: fN 0 en [xi,xi +1 1i=1,n-1 f"(xl f"(xm) o f "(x¡) - f "(xi) = 0, i = 2, n -1, k = 0,1,2 x f m( i) fM(xn ) 38 fm(xi) f(x n) -yn 8n (x45 - y` 2 Irene Sánchez Guevara sp(x)= al +bi(x- xi) +ci(x-xi)2 +di(x-xi)3 para x E [xi, xi_1 ] ¡=1,n-1, p= 1 2,1 El mínimo corrresponde al spline natural cúbico s(x) (QTD2Q+pT)c=PQTy Después de derivar y aplicar las condiciones del mínimo se obtiene los coeficientes del spline a = y - p-1D2QC bi = Aa, - cihi - dihil di = 3 AC` hi = [xi+1 - xi] t i Matriz tridiagonal T Donde: tii=2(hi-hi1) i=1,...,m-2 para ¡ =1,..., m-3 ti+li = tii+l = h3, tij = 0 en cualquierotro caso D = diagonawl, w2,... , wn LL Matriz Q Donde: 1 1 1 qi +li =---hi hi+1 1 qi +2 iqi• = 0 hi+2 y i=1,...,m-2 en otro caso 39 Reflexiones Finiseculares: las Matemáticas en las Ciencias Sociales Como se puede observar el cálculo fuerte está en la solución del sistema (1), pero debido a que las matrices son tridiagonales, la solución es muy estable desde el punto de vista numérico. El cálculo del parámetro de alisamiento, que recordemos es uno de los problemas de los métodos de suavizamieno, ese se hace mediante una función de discrepancia.' El algoritmo para esta técnica es el siguiente: Algoritmo o Entrada (Cs>o:p>o) 1 Calculo del vector c 1.1 Resolución del sistema (Q`D'Q +PkTF=PkQ`Y 1.2 Cálculo de la función de discrepancia 1.2.1 v = pk'c 1.2.2 t0(Pk) = v 'Q`D2Qv 2 Para 1_>1 se prueba convergencia 2.1 I(p(pk)-Csl«, 2. 2 j & -Pk-II«2 _ ¿ Existe convergencia ? Sí, ir a 5; No, ir a 3 3 Resolución del sistema: (Q`DZQ + pkT)avP = Tv Y se calcula (P'(Pk) = 2v`Q`D2Q P ' Ver Sánchez Guevara, Irene, Alisamiento de Datos. Teoría y métodos numéricos. Avances de investigación , núm. 16, UAM, DCSH , Política y Cultura, México, 1991. 40 Irene Sánchez Guevara 4 Cálculo del parámetro Pk+l - Pk + rP(Pk ) 9, V k regresar al paso 1 5 Cálculo de los coeficientes Spline a=Y-Pk'D2Qc d . =AC' 3h; i = l m- 1 d.=AC, - i=1m-1 3h; 6 Fin Observar que solo se hizo un cálculo del sistema : (Q`D2Q)+PkT) Se hizo un programa para probar el algoritmo , el siguiente es el diagrama del programa 41 Reflexiones Finiseculares : las Matemáticas en las Ciencias Sociales Alisa Lee: Datos .y cota Alisi n t 42 Alisa 1 cálculo de coeficien te spline Impresión Opciones 1. Otras evaluaciones 2. Cambio de Cs 3. Oro conjunto de. datos 4. Terminar Irene Sánchez Guevara EJEMPLO Considere el siguiente conjunto de datos que corresponde a los pagos mensuales de teléfono de los últimos dos años de una compañía Mes t 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Pago y 362 385 432 341 382 409 498 387 473 513 582 474 544 582 681 557 628 707 773 592 627 725 854 661 Gráfica 1 Después de introducir los datos en el programa alisa, nos da una cota máxima de 82,300 aproximadamente, con lo que se tendría la recta de mínimos cuadrados. Así con una cota de 80,000 se tiene un ajuste a una recta de mínimos cuadrados. 43 Reflexiones Finiseculares: las Matemáticas en las Ciencias Sociales Mes t 1 Pago 362 yea l cota=80,000 datos alisados cota= 80,000 369.04 2 3 4 5 6 7 8 9 10 11 12 13 385 432 341 382 409 498 387 473 513 582 474 544 376.48 383.35 390.48 401.22 416.14 433.59 452.20 473.65 496.40 518.00 538.22 560.22 14 15 16 17 582 681 557 628 583.70 606.30 626.34 646.05 300 18 19 20 21 22 707 773 592 627 725 663.95 676.80 685.80 697.53 712.77 100 23 24 854 661 726.27 734.57 900 ♦ '' 800 700 • ♦ 600 ♦ ♦ ' • ♦ 500 $ 400 200 0 0 10 20 30 mes Gráfica 2 Si se elige la cota de 40,000, se reproduce con un mínimo error los datos de la tabla, sólo que ahora se tiene una función continua. A continuación se presenta los cálculos y las gráficas con dos cotas diferentes: 44 Irene Sánchez Guevara Pago 362 385 432 341 382 409 498 387 y cal Cs=80,000 369.04 376.48 383.35 390.48 401 . 22 416.14 433.59 452. 20 y cal con Cs=40,000 361.80 385.60 430.90 342.16 381.10 410.19 496.20 388.70 473 473.65 471.80 513 582 474 544 582 681 557 628 707 773 592 627 725 496.40 518.00 538.22 560.22 583.70 606.30 626.34 646.05 663.95 676.80 685.80 697.53 712.77 514.12 580.44 475.60 542.80 583.34 679.14 558.64 627.10 707.98 771.24 593.62 626.16 726.05 854 726.27 852.65 661 734. 57 661.57 Gráfica 3 45 Reflexiones Finiseculares: las Matemáticas en las Ciencias Sociales CONCLUSIONES La técnica de suavizamiento o alisamiento con funciones Spline toma las ventajas de los métodos de suavizamiento y el procedimiento presentado calcula automáticamente el parámetro de alisamiento, es más eficiente que la interpolación polinomial global porque los cálculos matriciales son más eficientes, además genera una función sobre todo el intervalo de observación con lo que se pueden obtener cálculos intermedios. En este trabajo se presentó la técnica solo para una variable, en trabajos posteriores se presentará para varias variables. El algoritmo se implementó en lenguaje FORTRAN, posteriormente se hará la programación con MATLAB. 46 REFERENCIAS BIBLIOGRÁFICAS Ahlberg; Nilson Walsh. The Theory Of Splines And TheirApplications, Mathematics in Science and Engineering, vol 38, Academic Press, N.Y. 1967. Makridakis, Wheelwright, McGee. Forecasting Methods and Applications, 2°Ed. Wiley, 1983. Reinsh, C. H. Smoothing by Sline Funtions, Number. Math. lo 1967. pp. 177-183. Sánchez G. I. Alisamiento de datos teoría y métodos numéricos, col. Avances de Investigación núm. 16, UAM-X, México. 47