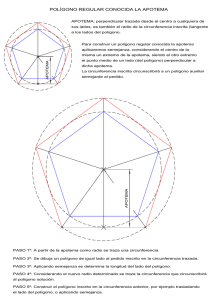
9.- Aplicaciones de la Trigonometría. En un polígono. 1. Calcular el

1º BCN-BT
Trigonometría
9.- Aplicaciones de la Trigonometría.
En un polígono.
A
B
A
C
B
C
1. Calcular el ángulo central dividiendo 360º por el número de lados del polígono.
Posteriomente dividimos por la mitad para obtener un triángulo rectángulo. Con ese ángulo
ya podemos calcular calcular el lado BC del polígono.
2. Apotema es una línea perpendicular trazada desde el centro de un polígono regular al punto
medio de uno de sus lados, que podemos calcular a partir del ángulo calculado en el punto
anterior
3. El área del polígono podemos obtenerla a partir de la fórmula:
perímetro· apotema
Área=
. También si conocemos el área del triángulo rectángulo que
2
forman la apotema con A y B y posteriomente lo multiplicamos por el número de triángulos
que hay dentro del polígono.
4. Radio de la circunferencia inscrita en el polígono que es igual a la apotema.
Ejemplo.- Un niño está haciendo volar una cometa. Ha soltado ya 47 metros de hilo y averigua que
el ángulo que forma la cuerda de la cometa con la horizontal es de 52º. ¿A qué altura se encuentra la
cometa?.
Llamamos h al cateto opuesto al ángulo conocido. El hilo, cuya longitud conocemos, es la
hipotenusa. Por tanto, la razón trigonométrica que debemos usar es el seno:
sen 52º =
h
47
→ h = 47 sen 52º = 47 · 0,788 = 37,036 m
Es decir, la cometa está a unos 37 metros del suelo.
Ejemplo.- Resuelve el triángulo ABC en el que conocemos un cateto c = 12 m y el ángulo B = 25º.
Los elementos desconocidos del triángulo miden: C = 90º - B = 90º - 25º = 65º.
b
tg 25º =
⇒ b = 12 · tg 25º = 5,60m
12
12
12
cos 25º =
⇒ a=
= 13,24m
a
cos 25º
Ejemplo.- Resuelve el triángulo ABC en el que conocemos C = 14º 26´y la hipotenusa a = 40m.
B= 90º - C = 90º - 14º 26´= 75º 34´
Página 1 de 5
c
⇒ c = 40 · sen 14º 26´= 9,97 m
40
b
cos 14º 26´=
⇒ b = 40 · cos 14º 26´= 38,74m
40
Ejemplo.- Resuelve el triángulo ABC en el que conocemos los dos catetos b = 25 m y c = 42,5 m.
a = 25 2 + 42,5 2 = 49,31m
25
42,5
tg B =
⇒ B = 30º 27´56´´
tg C =
⇒ C = 59º 42´4´´
42,5
25
Ejemplo.- En las carreteras de montaña es normal encontrarse con señales de tráfico que indican el
porcentaje de pendiente. Calcula el ángulo de una carretera cuya señal de tráfico indica un 12% de
pendiente.
Esta señal indica que por cada 100 metros en horizontal la subida es de 12 metros. La carretera sería
la hipotenusa del triángulo. Para saber el ángulo, conocidos los dos catetos, calculamos la tangente
y posteriormente el ángulo.
12
tg B =
⇒ B = 6º50´34´´
100
o sea, que una pendiente del 12% se corresponde con una inclinación de casi 7º.
Ejemplo.- Queremos conocer la altura de una montaña y sólo disponemos del ángulo de
observación de la montaña que es de 26º. Si nos acercamos 100 metros, el ángulo de observación
aumenta hasta 35º. Con estos datos, ¿calcula la altura de la
montaña?.
Tenemos dos triángulos. Las incógnitas que vamos a
manejar son: h que será la altura de la montaña y x la distancia
del segundo punto de observación al centro de la montaña. En
ambos triángulos podemos utilizar la tangente, que relaciona
el ángulo con los dos catetos:
h
tg 35º =
⇒ h = x · tg 35º ⇒ h = 0,7 x
x
h
tg 26º =
⇒ h = ( x + 100) · tg 35º ⇒ h = ( x + 100) · 0,49
x + 100
se resuelve el sistema de dos ecuaciones con dos incognitas:
49
0,7 x = ( x + 100) · 0,49 ⇒ 0,7 x = 0,49 x + 49 ⇒ x =
= 233 m
0,21
Por lo tanto, la altura será:
h = 0,7 x = 0,7 · 233 ⇒ h = 163 m
Ejercicios de polígonos.
Ejercicio.- La fuente de la Plaza del Duque, calcular el ángulo central, la apotema, el área del
polígono y el redio de la circunferencia inscrita.
Lado de un polígono.
1. La longuitud de la apotema de un polígono regular de 9 lados es de 20 cm. Calcular el lado.
Solución. Lado = 14,55 cm.
2. La longuitud de la apotema de un polígono regular de 12 lados es de 27 cm. Calcular el lado.
sen 14º 26´=
Página 2 de 5
1º BCN-BT
Trigonometría
Solución. Lado = 13,97 cm.
3. La longuitud de la apotema de un polígono regular de 6 lados es de 10 cm. Calcular el lado.
Solución. Lado = 11,54 cm.
4. La longuitud de la apotema de un polígono regular de 5 lados es de 8 cm. Calcular el lado.
Solución. Lado = 9,4 cm.
5. La longuitud de la apotema de un polígono regular de 10 lados es de 21 cm. Calcular el lado.
Solución. Lado = 12,97 cm.
Apotema de un polígono.
6. La longuitud del radio de un polígono regular de 9 lados es de 29 cm. Calcular la apotema.
Solución, apotema = 27,25 cm.
7. La longuitud del radio de un polígono regular de 5 lados es de 22 cm. Calcular la apotema.
Solución, apotema = 15,14 cm.
8. La longuitud del radio de un polígono regular de 10 lados es de 13 cm. Calcular la apotema.
Solución, apotema = 12,36 cm.
9. La longuitud del radio de un polígono regular de 12 lados es de 26 cm. Calcular la apotema.
Solución, apotema = 25,11 cm.
10. La longuitud del radio de un polígono regular de 6 lados es de 31 cm. Calcular la apotema.
Solución, apotema = 26,84 cm.
Área de un polígono.
11. La longuitu del lado de un polígono regular de 10 lados es de 12 cm. Calcular el área.
Solución Área = 1107,96 cm2.
12. La longuitu del lado de un polígono regular de 8 lados es de 14 cm. Calcular el área.
Solución Área = 946,37 cm2.
13. La longuitu del lado de un polígono regular de 9 lados es de 27 cm. Calcular el área.
Solución Área = 2388 cm2.
14. La longuitu del lado de un polígono regular de 5 lados es de 11 cm. Calcular el área.
Solución Área = 287,69 cm2.
15. La longuitu del lado de un polígono regular de 12 lados es de 30 cm. Calcular el área.
Solución Área = 10076,53 cm2.
Radio de un polígono.
16. La longuitud de la apotema de un polígono regular de 9 lados es de 13 cm. Calcular el radio.
Solución: radio = 13,83 cm.
17. La longuitud de la apotema de un polígono regular de 8 lados es de 18 cm. Calcular el radio.
Solución: radio = 23,51 cm.
18. La longuitud de la apotema de un polígono regular de 12 lados es de 6 cm. Calcular el radio.
Solución: radio = 11,59 cm.
19. Calcular el radio de la circunferencia inscrita en un polígono regular de 6 lados si el lado
mide 32 cm. Solución. radio = 27,71 cm.
20. Calcular el radio de la circunferencia inscrita en un polígono regular de 12 lados si el lado
mide 26 cm. Solución. radio = 48,51 cm.
Altura de un avión.
21. Dos pesonas separadas 500 m ven un avión que vuela sobre ellos con ángulos de elevación
de 50º y 75º. ¿A qué altura vuela el avión?. Solución: altura = 451,65 m.
22. Dos pesonas separadas 620 m ven un avión que vuela sobre ellos con ángulos de elevación
de 58º y 33º. ¿A qué altura vuela el avión?. Solución: altura = 286,4 m.
Página 3 de 5
23. Dos pesonas separadas 610 m ven un avión que vuela sobre ellos con ángulos de elevación
de 62º y 43º. ¿A qué altura vuela el avión?. Solución: altura = 380,28 m.
24. Dos pesonas separadas 860 m ven un avión que vuela sobre ellos con ángulos de elevación
de 61º y 34º. ¿A qué altura vuela el avión?. Solución: altura = 422,21 m.
25. Dos pesonas separadas 310 m ven un avión que vuela sobre ellos con ángulos de elevación
de 78º y 46º. ¿A qué altura vuela el avión?. Solución: altura = 263,1 m.
Altura de un árbol.
26. Determina la altura de un árbol si desde un punto situado a 5 metros de su base se observa
su copa con un ángulo de 46º. Solución: altura = 5,17 m.
27. Determina la altura de un árbol si desde un punto situado a 8 metros de su base se observa
su copa con un ángulo de 19º. Solución: altura = 2,75 m.
28. Determina la altura de un árbol si desde un punto situado a 50 metros de su base se observa
su copa con un ángulo de 24º. Solución: altura = 22,26 m.
29. Determina la altura de un árbol si desde un punto situado a 27 metros de su base se observa
su copa con un ángulo de 12º. Solución: altura = 5,73 m.
30. Determina la altura de un árbol si desde un punto situado a 85 metros de su base se observa
su copa con un ángulo de 415º. Solución: altura = 22,77 m.
Altura de una cometa.
31. La longuitud del hilo que sujeta una cometa es de 210 m. Si el ángulo de elevación de la
cometa es de 34º, ¿qué altura alcanza la cometa?. Solución altura = 117,4 m.
32. La longuitud del hilo que sujeta una cometa es de 70 m. Si el ángulo de elevación de la
cometa es de 53º, ¿qué altura alcanza la cometa?. Solución altura = 55,4 m.
33. La longuitud del hilo que sujeta una cometa es de 160 m. Si el ángulo de elevación de la
cometa es de 64º, ¿qué altura alcanza la cometa?. Solución altura = 143,8 m.
34. La longuitud del hilo que sujeta una cometa es de 90 m. Si el ángulo de elevación de la
cometa es de 14º, ¿qué altura alcanza la cometa?. Solución altura = 21,7 m.
35. La longuitud del hilo que sujeta una cometa es de 130 m. Si el ángulo de elevación de la
cometa es de 73º, ¿qué altura alcanza la cometa?. Solución altura = 124, 3 m.
Altura de una montaña.
36. Para medir l altura de una montaña se miden los ángulos de elevación desde dos puntos
situados a una distancia de 330 m y a una altitud de 690 m sobre el nivel del mar. ¿Cuál es la
altura de la montaña si los ángulos son 35º y 46º?. Solución. altura = 713,57, altura + altura
nivel del mar = 1403,57 m
37. Para medir l altura de una montaña se miden los ángulos de elevación desde dos puntos
situados a una distancia de 490 m y a una altitud de 1850 m sobre el nivel del mar. ¿Cuál es
la altura de la montaña si los ángulos son 19º y 21º?. Solución. altura = 1638,12, altura +
altura nivel del mar = 3488,12 m
38. Para medir l altura de una montaña se miden los ángulos de elevación desde dos puntos
situados a una distancia de 200 m y a una altitud de 1410 m sobre el nivel del mar. ¿Cuál es
la altura de la montaña si los ángulos son 36º y 41º?. Solución. altura = 884,9, altura + altura
nivel del mar = 2294,9 m
39. Para medir l altura de una montaña se miden los ángulos de elevación desde dos puntos
situados a una distancia de 410 m y a una altitud de 800 m sobre el nivel del mar. ¿Cuál es la
altura de la montaña si los ángulos son 47º y 62º?. Solución. altura = 1022,93, altura + altura
nivel del mar = 1822,93 m
Página 4 de 5
1º BCN-BT
Trigonometría
40. Para medir l altura de una montaña se miden los ángulos de elevación desde dos puntos
situados a una distancia de 410 m y a una altitud de 800 m sobre el nivel del mar. ¿Cuál es la
altura de la montaña si los ángulos son 47º y 62º?. Solución. altura = 1022,93, altura + altura
nivel del mar = 1822,93 m
Página 5 de 5