TEMA 1 - RUA - Universidad de Alicante
Anuncio
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
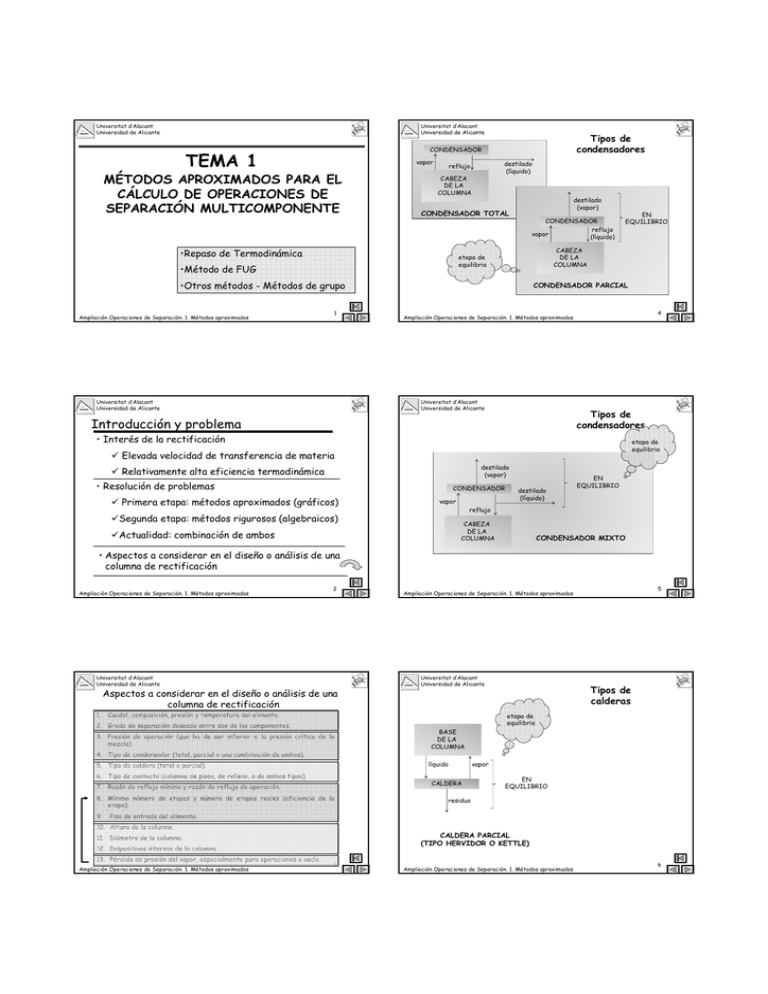
Tipos de
condensadores
CONDENSADOR
TEMA 1
vapor
MÉTODOS APROXIMADOS PARA EL
CÁLCULO DE OPERACIONES DE
SEPARACIÓN MULTICOMPONENTE
destilado
(líquido)
reflujo
CABEZA
DE LA
COLUMNA
destilado
(vapor)
CONDENSADOR TOTAL
CONDENSADOR
reflujo
vapor
(líquido)
•Repaso de Termodinámica
CABEZA
DE LA
COLUMNA
etapa de
equilibrio
•Método de FUG
•Otros métodos - Métodos de grupo
Ampliación Operaciones de Separación. 1. Métodos aproximados
1
Universitat d’Alacant
Universidad de Alicante
EN
EQUILIBRIO
CONDENSADOR PARCIAL
4
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Tipos de
condensadores
Introducción y problema
• Interés de la rectificación
etapa de
equilibrio
Elevada velocidad de transferencia de materia
destilado
(vapor)
Relativamente alta eficiencia termodinámica
• Resolución de problemas
CONDENSADOR
Primera etapa: métodos aproximados (gráficos)
vapor
destilado
(líquido)
EN
EQUILIBRIO
reflujo
Segunda etapa: métodos rigurosos (algebraicos)
CABEZA
DE LA
COLUMNA
Actualidad: combinación de ambos
CONDENSADOR MIXTO
• Aspectos a considerar en el diseño o análisis de una
columna de rectificación
Ampliación Operaciones de Separación. 1. Métodos aproximados
2
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Tipos de
calderas
Aspectos a considerar en el diseño o análisis de una
columna de rectificación
1.
5
Ampliación Operaciones de Separación. 1. Métodos aproximados
Caudal, composición, presión y temperatura del alimento.
etapa de
equilibrio
2. Grado de separación deseado entre dos de los componentes.
3. Presión de operación (que ha de ser inferior a la presión crítica de la
mezcla)
BASE
DE LA
COLUMNA
4. Tipo de condensador (total, parcial o una combinación de ambos).
líquido
5. Tipo de caldera (total o parcial).
6. Tipo de contacto (columna de pisos, de relleno, o de ambos tipos).
CALDERA
7. Razón de reflujo mínima y razón de reflujo de operación.
8. Mínimo número de etapas y número de etapas reales (eficiencia de la
etapa).
9.
vapor
EN
EQUILIBRIO
residuo
Piso de entrada del alimento.
10. Altura de la columna.
CALDERA PARCIAL
(TIPO HERVIDOR O KETTLE)
11. Diámetro de la columna.
12. Dispositivos internos de la columna.
13. Pérdida de presión del vapor, especialmente para operaciones a vacío.
Ampliación Operaciones de Separación. 1. Métodos aproximados
3
Ampliación Operaciones de Separación. 1. Métodos aproximados
6
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Tipos de
calderas
DISEÑO PRELIMINAR DE LA COLUMNA
piso N
xN
Recta
operativa
yN
1. Análisis de la composición del
alimento; Balances de materia
preliminares
yT
Mezcla
parcialmente
vaporizada
(xT, yT)
líquido
xT xB xN
TERMOSIFÓN
Residuo, xB
CALDERA PARCIAL
(TIPO TERMOSIFÓ
TERMOSIFÓN, CON
ETRACCIÓ
ETRACCIÓN DE LÍ
LÍQUIDO DEL
FONDO DE LA COLUMNA)
El líquido xN se cruza
con el vapor yT, pero
no se obtiene el
residuo de
composición xT, sino
xB, que resulta de
mezclar las
corrientes de
composición xN y xT
2. Recopilación de los datos
necesarios
3. Método FUG
Estimación
preliminar de costes
Proporciona
una fracción
de etapa
de equilibrio
Ampliación Operaciones de Separación. 1. Métodos aproximados
Separación
factible
10
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Tipos de
calderas
Termodinámica clásica del equilibrio entre fases
Condiciones del equilibrio entre fases
piso N
Recta
operativa
yN
xN
líquido, xN
TERMOSIFÓN
mezcla parcialmente
vaporizada (xT, yT)
residuo, xB
P
CALDERA PARCIAL
(TIPO TERMOSIFÓ
TERMOSIFÓN, CON
ETRACCIÓ
ETRACCIÓN DE LÍ
LÍQUIDO DEL
DOWNCOMER DEL ÚLTIMO PISO DE
DE LA COLUMNA)
La composición xN = xB
ya que se extrae todo el
líquido del downcomer.
Equivale a:
TERMOSIFÓN
vapor a la
columna (yT)
=P
(1)
µ2
(1)
(2)
= µ1
(2)
= ... = µ1
(2)
= ... = µ 2
= µ2
.
= ... = P
.
µc
(1)
= µc
( π)
( π)
SdT − VdP + ∑ n i dµ i = 0
( π)
dµ i = −si dT + v i dP
.
(2)
= ... = µ c
i
µ i (T , P) = µ i (T r , P r ) −
T
P
∫ si dT + ∫ v i dP
Tr
Pr
11
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
dµ i = −si dT + v i dP
Etapas en el diseño de una columna:
µ i (T , P) = µ i ( T r , P r ) −
1. DISEÑO PRELIMINAR
T
Pr
∂µ
Para un gas ideal, puro, teniendo en cuenta i = v i
∂P T
considerando la ecuación de estado del gas ideal:
vi =
3. ANÁLISIS DE RESULTADOS
P
∫ si dT + ∫ v i dP
Tr
Condiciones más
económicas
Razón de reflujo
Tamaño de la columna
2. CÁLCULO DETALLADO DE LA COLUMNA.
RT
Pi
e integrando, a temperatura constante:
µ i − µ i o = RT ln
Ampliación Operaciones de Separación. 1. Métodos aproximados
( π)
Residuo
líquido
(xB = xT)
Ampliación Operaciones de Separación. 1. Métodos aproximados
Tipo y disposición del equipo
Estimación preliminar de costes
(1)
µ1
xT = xB xN
Proporciona
una etapa
de equilibrio
La ecuación de Gibbs-Duhem:
expresa la relación existente
entre las c+2 variables que
caracterizan el estado de un
sistema heterogéneo cerrado:
T (1) = T (2) = ... = T ( π)
yT
9
Pi Gases reales
f
µ i − µ i o = RT ln io
Pi º
fi
Ampliación Operaciones de Separación. 1. Métodos aproximados
12
y
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
condición de equilibrio entre las fases α y β (a P y T
constantes) :
α
fi = fi
v
β
Correlación de Pitzer y Curl y de O’Connell y Prausnitz para el
cálculo de Bij ,
Para gases puros NO polares:
v
fi = ϕi (Py i )
Bii =
L
0L
0
fi = ai fi0L = γ i x i ϕi Pi ψ i
(
v o P − Pi o
ψ i = exp i
RT
RTci ( NP )
f
TR i , ωi
Pci
(
con TR i = T
)
Po
ωi ≡ − log10 i
Pc
i
Tci
f ( NP ) = 0.1445 −
• Cálculo del coeficiente de
fugacidad
)
− 1.000
T / Ti c = 0.7
0.330 0.1385 0.0121
−
−
+
2
3
TR i
TR
TR
i
i
0.46 0.50 0.097 0.0073
ωi 0.073 +
−
−
−
2
2
3
8
TR i
TR i
TR i
TR i
• Cálculo del coeficiente de
actividad
13
Ampliación Operaciones de Separación. 1. Métodos aproximados
16
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Cálculo del coeficiente de fugacidad del vapor
Para gases puros polares:
f
1 P ∂V
RT
dP
ln ϕ i = ln i =
−
∫
y i P RT 0 ∂n i T ,P ,n
P
j
B ii =
volumen molar parcial del componente i
ECUACIÓN DE ESTADO
∂V
vi =
∂n i T,P,n
RTci ( NP )
f
TR i , ω i H + f ( µ ) TR i , µ R i + f ( AS ) TR i , η i
Pc i
[ (
)
(
(
)]
Gases no polares
f(NP)
f(AS)
f(µ)
Asociación
Momento dipolar
j
Ampliación Operaciones de Separación. 1. Métodos aproximados
)
Distinto valor
dependiendo del valor de
µR
14
17
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
donde, si µRi
Ecuació
Ecuación de estado virial
Pv = RT + BmezclaP
(
≥4
)
(
f ( µ ) TR i , µ R i = −5.237220 + 5.665807 ln µ R i − 2.133816 ln µ R i
(
m
P
ln ϕ i = 2 ∑ y j Bij − B mezcla
j = 1
RT
0.2525373 ln µ R i
(
2.283270 ln µ R i
(
Bij = Bji
)
)
)
2
3
B mezcla = ∑ ∑ y i y j Bij
Ampliación Operaciones de Separación. 1. Métodos aproximados
[
(
− 0.2649074 ln µ R i
[ (
)]
)
(
)
3
y si µRi < 4:
(
)
f ( µ ) TR i , µ R i = f ( AS) TR i , η i = 0
i =1 j =1
15
2
+
1
+
5.769770 − 6181427
.
ln µ R i +
TR i
f ( AS) TR i , η i = − η i exp 6.6 0.7 − TR i
m m
)
Ampliación Operaciones de Separación. 1. Métodos aproximados
18
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Cálculo de la fugacidad del líquido
ωiH es el factor acéntrico del homomorfo del cuerpo i (un
hidrocarburo con aproximadamente el mismo tamaño y la
misma forma que la molécula polar).
µRi es el momento dipolar reducido
µRi =
105 µ i 2 Pc i
Tc i
2
µi es el momento dipolar en Debye, Pci la presión crítica en
atm y Tci la temperatura crítica en K.
Funciones de exceso
G E = G disolucion real a P,T, x − G disolucion ideal a P,T, x
∂M
m i =
∂n i T ,P ,n j
a i ( T, P , x) ≡
∂M E
E
m i =
∂n i
T,P ,n j
γi =
E
g i E = RT ln γ i
M = ∑ n i mi
i
M E = ∑ n i mi
19
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
f i ( T, P , x)
f i ( Tº , P o , x o )
ai
xi
i
22
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
ηi es un coeficiente que sólo es distinto de cero para
las moléculas que tienden a dimerizarse en fase vapor.
Modelos para el cálculo de γi
Las contribuciones debidas al momento dipolar y a la
constante de asociación son despreciables para TR >
0.95 ya que son muy débiles
Modelos empíricos
Bij → reemplazar Pci por Pcij, Tci por Tcij, ωi por ωij, µRi
por µRij y ηi por ηij y utilizar las siguientes reglas de
mezcla:
Modelos de coeficientes de actividad o de entalpía libre de
exceso
Modelos basados en el concepto de
composición local
Ecuación de Margules
Ecuación de Van Laar
Ecuación de Wilson
Ecuación de Heil
Ecuación de Redlich-Kister
Ecuación NRTL
Ecuación UNIQUAC
Ecuación de Black
Ecuación LEMF (Local Effective Mole Fraction)
Ecuaciones de Estado
Modelos de contribución de grupos
ASOG (Analytical Solution Of Groups)
UNIFAC (UNIQUAC Functional-groups Activity Coefficients)
20
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
(
Tc ij = Tc i Tc j
ω ij =
Universitat d’Alacant
Universidad de Alicante
2
ηij =
ωi + ω j
ηi + η j
Pc v c
P v
i i + cj cj
T
Tc j
ci
(v
1
ci
3
+ vc j
1
3
)
3
es el volumen crítico de i.
µ R ij =
105 µ i µ j Pc ij
Tc ij 2
Ampliación Operaciones de Separación. 1. Métodos aproximados
ω ij =
2
ωiH + ω j
2
i polar, j no polar
ω ij H =
23
Ecuación de Wilson
m
m
gE
= − ∑ x i ln ∑ x j Λ ij
RT
j =1
i =1
2
Pc ij = 4Tc ij
vci
)
1
Ampliación Operaciones de Separación. 1. Métodos aproximados
ω i H + ω jH
2
i y j polares
λ ij − λ ii
exp −
RT
λ ij − λ jj
v
Λ ji = i exp −
vj
RT
Λ ij =
vj
vi
m x Λ
m
ln γ k = − ln ∑ x j Λ kj + 1 − ∑ m i ik
j =1
i =1
∑ x j Λ ij
j =1
21
Ampliación Operaciones de Separación. 1. Métodos aproximados
24
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Ecuación NRTL (Non-Random, Two-Liquid)
m
E
m
g
= ∑ xi
RT i = 1
∑ τ ji G ji x j
∑ G li x l
ln γ i =
(
) (α ji = α ij )
m
∑ τ ji G ji x j m x G ∑ x r τ rjG rj
j =1
j ij r = 1
ln γ i = m
+∑ m
m
l =1
G
x
G
x
G
x
∑ li l
∑ lj l ∑ lj l
l =1
l =1
l =1
Ampliación Operaciones de Separación. 1. Métodos aproximados
25
m
Φ* z m
θ
g E (combinatorial)
= ∑ x i ln i + ∑ q i x i ln i *
RT
xi
2 i =1
Φi
i =1
m
m
g E ( residual)
= − ∑ q i x i ln ∑ θ j τ ji
RT
j=1
i =1
ri x i
m
θi =
depende sólo de la
composición y del tamaño y
forma de las moléculas
depende también de las fuerzas
intermoleculares
r y q: parámetros de estructura molecular de compuestos
puros. Dependen del tamaño molecular y del área superficial
j
j=1
Ampliación Operaciones de Separación. 1. Métodos aproximados
Modelo UNIFAC
ri = ∑ ν k ( i ) R k
k
q i = ∑ ν k ( i )Q k
Rk y Qk son los parámetros de volumen y área,
respectivamente, para el grupo funcional de tipo k.
k
(
ln γ i R = ∑ ν k ( i ) ln Γk − ln Γk ( i )
Γk es el coeficiente de actividad residual del grupo
funcional k en la mezcla real y Γk(i) es la misma
magnitud, pero en una mezcla de referencia que
solamente contiene moléculas de tipo i
k =1
z
r − q j − rj − 1
2 j
) (
)
z es el número de coordinación, z = 10
Ampliación Operaciones de Separación. 1. Métodos aproximados
)
θ T
ln Γk = Q k 1 − ln ∑ θ m Tmk − ∑ m mk
m
m ∑ θ n Tnm
n
m
(
νki es el número de grupos funcionales de tipo k en la
molécula i
k
q i xi
Para cada mezcla
∑ q jx j
binaria, hay dos
j=1
parámetros
m
Φi* z
θi
Φ i* m
τij y τji
ln γ i = ln
+ q i ln * + l i −
∑ x l − q i ln ∑ θ j τ ji + ajustables
xi
x i j=1 j j
2
Φi
que dependen de
j=1
las energías
m
θ j τ ij
q il i − q i ∑ m
características
j=1
∆uij y ∆uji
∑ θ k τ kj
lj =
28
Universitat d’Alacant
Universidad de Alicante
Ecuación UNIQUAC (Universal Quasi-Chemical Theory)
j
1 − xi
2
• Aii = Ajj = 0. En general, los valores de Aij se
encuentran en la bibliografía
Universitat d’Alacant
Universidad de Alicante
∑r x
j =1
c
x i ∑ ( x jA ij )
• Está restringida a las condiciones en que todas las
parejas Aij y Aji son del mismo signo
m
Φi =
j =1
1 −
c
c
x i ∑ ( x jA ij ) + ( 1 − x i ) ∑ x jA ij
j =1
j =1
g ji − g ii
RT
G ji = exp −α ji τ ji
*
c
∑ ( x jA ij )
j=1
m
l =1
τ ji =
Ecuación de Van Laar
26
Universitat d’Alacant
Universidad de Alicante
Ampliación Operaciones de Separación. 1. Métodos aproximados
29
Universitat d’Alacant
Universidad de Alicante
Para cada mezcla binaria, hay dos parámetros ajustables τij y τji que
dependen de las energías características ∆uij y ∆uji
θm =
∆u ij
a ij
τ ij = exp −
≡ exp −
RT
T
X mQ m
∑ Xn Qn
Modelo UNIFAC (continuación)
fracción de área del grupo m
n
∑ ν m( j )x j
Xm =
∆u ji
a ji
τ ji = exp −
≡ exp −
RT
T
j
∑ ∑ ( νn( j )x j )
fracción molar del grupo m en la
disolución
j n
a
Tmk = exp − mk
T
parámetro de interacción de grupo
• amk akm. Cuando m = k, amk = 0 y Tmk = 1.0
• Los valores de Rk, Qk, amk y akm se encuentran en la bibliografía
Ampliación Operaciones de Separación. 1. Métodos aproximados
27
Ampliación Operaciones de Separación. 1. Métodos aproximados
30
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
SELECCIÓ
SELECCIÓN DEL MODELO TERMODINÁ
TERMODINÁMICO
1. Caracterizar la mezcla:
mezcla
Gases ligeros (LG)
Hidrocarburos (HC)
Compuestos orgánicos polares (PC)
Disoluciones acuosas (A) con o sin electrolitos (E)
2.
A sin PC
DE PREDECIR DE MANERA
Seleccionar algún modelo
especial, dependiendo del
tipo de solutos
No
E
UNA VEZ HECHA LA SELECCIÓN
DEL MODELO ES FUNDAMENTAL
COMPROBAR QUE ÉSTE ES CAPAZ
Sí
ADECUADA LOS DATOS DE
EQUILIBRIO EXPERIMENTALES
NRTL modificado
Ampliación Operaciones de Separación. 1. Métodos aproximados
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Amplio
intervalo de
Tb de
compuestos
puros
HC con o sin LG
Modelo de estados
correspondientes de
Lee-Kesler-Plöcker
Sí
No
Se fijan P y composición
del líquido saturado
APLICACIÓN DEL
CÁLCULO DEL
EQUILIBRIO ENTRE
FASES AL
EQUILIBRIO
LÍQUIDO-VAPOR
Se estiman yi y T
Se calcula ki
Nuevos yi
Se calcula yi = kixi
NO
Abs(yi,sup -yi,calc)<<<
La selección depende de P y T
Todas P y T
Peng-Robinson
Todas P y T no
Todas T, P<Pc
criogénicas
SRK
Benedict-Webb-Rubin-Starling
SI
Cálculo de Tb
NO
Nueva T
Σkixi=1
Cálculo de Tr
SI
FIN
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Mezcla con PC
Cálculo a partir de las
volatilidades relativas
Universitat d’Alacant
Universidad de Alicante
LG
Sí
35
Ampliación Operaciones de Separación. 1. Métodos aproximados
yi
= αi x i
Kb
PSRK
xiKb =
No
Modelo de coeficientes de actividad
1
=
Kb
c
∑ αixi
ó
i =1
Kb =
1
c
∑ αixi
i =1
yi
αi
y
∑ αii = K b
volatilidades independientes de T: xi o yi → Kb → T a partir de Kb = f(T).
Hay
parámetros
binarios
Sí
Hay 2 fases
líquidas
No
UNIFAC
Sí
NRTL,
UNIQUAC
volatilidades relativas dependientes de T : encontrar el valor de T que
anula la función f(T):
1 Tb
No
Wilson, NRTL
f (T ) = K b −
c
∑ αi x i
i =1
Ampliación Operaciones de Separación. 1. Métodos aproximados
yi
i =1 α i
c
F(T ) = K b − ∑
Ampliación Operaciones de Separación. 1. Métodos aproximados
Tr
36
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
• Cálculo de las temperaturas de burbuja y de rocío en
sistemas que contienen componentes que sólo se
encuentran presentes en una de las dos fases
Destilación súbita adiabática
Caso 1: se conoce la presión
y la temperatura
1) Cálculo
de destilació
n sú
destilacióde
slaúbita a T, P
operación y se desea calcular la temperatura del
2) sea
Cálculo
de H
alimento para que ésta
adiabática
c
HL = ∑ HLi x i
3) Cálculo de TF para que HF = H
i=1
f (T ) = ∑ K i x i − 1 − ∑ y L
i≠ H ,L
L
c
HV = ∑ HVi y i
i =1
y
F(T) = ∑ i − 1 − ∑ x H
i ≠ H,L K
H
i
Cámara de destilación
ALIMENTO
(líquido o vapor)
F, zi, HF, TF, PF
V, y, HV
T, P
V
L
H = HV + HL
F
F
L, x, HL
Q
(aportado o eliminado)
c
HF = ∑ HFizi
i =1
37
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Ampliación Operaciones de Separación. 1. Métodos aproximados
40
Universitat d’Alacant
Universidad de Alicante
Destilación súbita en condiciones
isotérmicas
Destilación súbita adiabática
Caso 2: Se conoce la entalpía del alimento y se
desea calcular la temperatura (o la presión) de
la operación para que ésta sea adiabática
Cámara de destilación
ALIMENTO
(líquido o vapor)
V, y, HV
F, zi, HF, TF, PF
T, P
1) Estimació
Estimación de T o P
L, x, HL
2) Cálculo de destilació
destilación sú
súbita a T, P
3) Cálculo de H
Q
(aportado o eliminado)
c
p(ψ) =
∑
4) Comprobació
Comprobación: ¿HF = H?
zi
i=1 1 − ψ(1 −
1
Ki
−1
)
38
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Destilación súbita isotérmica
Estimación inicial de xi, yi
Nueva estimación de xi, yi
Se calcula xi, yi a partir de ψ
FIN
Diferencia entre xi, yi
supuestas y calculadas <<
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
1. Composición del alimento: análisis del diagrama TER
Se calcula k = f (xi, yi, T, P)
SI
41
MÉTODOS APROXIMADOS PARA EL
CÁLCULO DE OPERACIONES DE
SEPARACIÓN MULTICOMPONENTE
Se fija F, z, P y T
Se calcula ψ a partir de p(ψ)
Ampliación Operaciones de Separación. 1. Métodos aproximados
2. Balance preliminar de materia: selección de componentes
clave
3. Presión de operación de la columna. Tipo de condensador
4. Métodos aproximados para el cálculo de columnas de
rectificación multicomponente: método FUG
NO
5. Métodos gráficos
39
6. Métodos de grupo
Ampliación Operaciones de Separación. 1. Métodos aproximados
42
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Composición del alimento: análisis del diagrama TER
En el caso de la destilación del petróleo y de otras
mezclas complejas:
Componentes desde C1 a C50 (Tb desde –162ºC
hasta 538ºC)
El nº de componentes con volatilidades
similares aumenta rápidamente con Tb (16 de los
18 isómeros del C8 hierven en un intervalo de
12ºC)
Los productos de la destilación de mezclas
complejas son también mezclas complejas
43
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Importancia (económica) de optimizar bien el alimento
Grupo
Caracterización de las fracciones del petróleo
Com.
Selecc.
T b (ºC)
Temp.
Grupo
Vol. Acumulado (%)
Vol. (%)
Densidad
(g/ml)(20ºC)
Densidad
Curvas de destilación
Análisis completo de fracción ligera
Tipo de hidrocarburos de las fracciones media
y pesada
Ensayos
normalizados
46
Ampliación Operaciones de Separación. 1. Métodos aproximados
Masa
molar
Número
de moles
Predicción de
propiedades
físicas
% molar
44
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
2
1
C6
C5
pentanos
hexanos
Iso3-Metilpentano
pentano
27.95
64.0
50
80
3
C7-H
heptanos
2-Metilhexano
90.4
103
4
C7-T
tolueno
Tolueno
110.6
121
5
C8
xilenos
Paraxileno
138.4
149
6
C9 mesitilenos
1,3,5-trimetilbenc
164.6
175
7
R
residuo
1,3-dietilbenceno
181.1
-
19.5
34.0
46.5
58.5
77.5
93
100.0
19.5
0.62
14.5
0.67
12.5
0.68
12.0
0.86
19.0
0.86
15.5
0.86
7.0
0.86
72.15
86.17
100.2
92.13
106.16
120.19
134.21
0.1672
0.1128
0.0848
0.1118
0.1536
0.1108
0.0448
21.3
14.4
10.8
14.2
19.5
14.1
5.7
Ampliación Operaciones de Separación. 1. Métodos aproximados
47
Universitat d’Alacant
Universidad de Alicante
PSEUDOCOMPONENTES
Hierve en un
margen estrecho
de T
Formado por
compuestos
similares
Pseudocomponente
Ampliación Operaciones de Separación. 1. Métodos aproximados
Intervalo de Tb
Tb media
Densidad media
Balances de
materia y energía
Masa molecular media
Se trata como un
componente puro
45
Ampliación Operaciones de Separación. 1. Métodos aproximados
48
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Balance preliminar de materia: selección
de componentes clave
VOLÁ
VOLÁTILES
0,7
0,7
o Separación de c componentes: c-1 columnas (1
columna separa a dos componentes)
0,6
0,6
Ampliación Operaciones de Separación. 1. Métodos aproximados
yy
0,4
0,4
METANO
METANO(LLK)
(LLK)
ETANO
ETANO(LLK)
(LLK)
PROPANO
PROPANO(LK)
(LK)
BUTANO
BUTANO(HK)
(HK)
0,3
0,3
PENTANO
PENTANO(HHK)
(HHK)
HEXANO
HEXANO(HHK)
(HHK)
0,2
0,2
0,1
0,1
00
Una columna no puede dividir a un alimento de
todas las formas posibles
El alimento y los productos han de cumplir el
balance de materia
PESADOS
0,5
0,5
o la calidad de dos productos puede caracterizarse
únicamente por la concentración de un
componente por cada corriente. Las
concentraciones de los otros componentes no
pueden elegirse arbitrariamente.
Piso
Piso11==condensador
condensador
Piso
Piso17
17==caldera
caldera
Piso
Piso10
10==piso
pisode
dealimentación
alimentación
PERFIL
PERFILDE
DEVAPOR
VAPOR
0,8
0,8
00
55
10
10
15
15
20
20
PISO
PISO
Volver a Método de Hengstebeck
49
Universitat d’Alacant
Universidad de Alicante
Ampliación Operaciones de Separación. 1. Métodos aproximados
52
Universitat d’Alacant
Universidad de Alicante
Seleccionar los componentes clave
Realizar suposiciones razonables acerca de la
separación en la columna
Realizar los balances de materia preliminares
Componente
C5
C6
C7-H
C7-T
C8
C9
R
Total
Fzi
21.3
14.4
10.8
14.2
19.5
14.1
5.7
100.0
DyDi
21.3
14.4
10.8-H
T
0
0
0
46.5 + (T - H)
RxRi
0
0
H
14.2-T
19.5
14.1
5.7
53.5 + (H - T)
ESPECIFICACIONES REPARTIDOS
SUPOSICIONES
NO REPARTIDOS
Ampliación Operaciones de Separación. 1. Métodos aproximados
50
Universitat d’Alacant
Universidad de Alicante
Ampliación Operaciones de Separación. 1. Métodos aproximados
53
Universitat d’Alacant
Universidad de Alicante
Presión de operación de la columna. Tipo
de condensador
• Componentes clave:
Componente clave ligero (LK)
Componente clave pesado (HK)
Especificar P en condensador + ∆P
• Componentes no clave (NK)
T del destilado de 10-50ºF (6-28ºC) superior a
T de entrada del agua de refrigeración
• Componentes HHK (HNK)
Si P se aproxima a P crítica, se trabaja a P
inferiores o se cambia de fluido refrigerante
• Componentes LLK (LNK)
• Componentes repartidos
Desventajas de aumentar P en el condensador
Ventajas de aumentar P en el condensador
Ampliación Operaciones de Separación. 1. Métodos aproximados
51
Ampliación Operaciones de Separación. 1. Métodos aproximados
54
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Composiciones
del destilado o
colas conocidas
o estimadas
Desventajas de aumentar P en el condensador
Calcular la presión PD del punto de
burbuja del destilado a 49ºC
(120ºF)
La volatilidad relativa disminuye: aumenta la
dificultad de la separación
PD a 30 psia si
PD<30 psia)
Hace aumentar la temperatura de la columna:
aumentan las reacciones secundarias
Por encima de 100 psig, hay que aumentar el
espesor del material de la columna
Calcular la presión PD
del punto de rocío del
destilado a 49ºC
(120ºF)
PD<365psia
(2.52MPa)
Utilizar
condensador
parcial
Calcular la T de
burbuja (TB) de
TB>temperatura de
descomposición de colas
o T crítica
TB<temperatura
de
descomposición
de colas o T
crítica
Disminuir
presión PD de
forma
aproximada
Fin
55
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Aumenta el punto de ebullición del destilado, lo que permite el uso
refrigerantes más baratos.
Si la columna opera por debajo de 1 atm, un aumento de presión,
disminuye el coste de creación y mantenimiento de vacío
Composiciones
del destilado o
colas conocidas
o estimadas
burbuja del destilado a 49ºC
(120ºF)
Por debajo de 1 atm disminuyen las fugas y por tanto el peligro
potencial de los materiales tóxicos o inflamables.
Ampliación Operaciones de Separación. 1. Métodos aproximados
56
Universitat d’Alacant
Universidad de Alicante
P
PD>215psia
PD<215psia
(1.48MPa)
utilizar
condensador
total (reponer
En la destilación de gases licuados, aumentan los puntos de
ebullición del líquido que circula por la columna, lo que permite
utilizar materiales de construcción más baratos.
Disminuye el diámetro de las tuberías y el tamaño de las válvulas
por las que circula el vapor.
Determinación
de P en el
condensador
Calcular la presión PD del punto de
Aumenta la densidad del vapor, y por tanto, la capacidad de la
columna
58
Ampliación Operaciones de Separación. 1. Métodos aproximados
Ventajas de aumentar P en el condensador
Comprobación de
la estabilidad de
las colas
las colas a PB
Para separaciones superatmosféricas, las
fugas son mayores, y aumenta el peligro
potencial
PD>365psia
Elegir un refrigerante para
operar el condensador
parcial a 415 psia(2.86 MPa)
Estimar la presión de colas (PB)
Aumenta la temperatura en la caldera
Ampliación Operaciones de Separación. 1. Métodos aproximados
Determinación
de P en el
condensador
PD>215psia
PD<215psia
(1.48MPa)
utilizar
condensador
total (reponer
PD a 30 psia si
PD<30 psia)
Pb<215 psia
Pcondensador
Pr
Pr
Calcular la presión PD
del punto de rocío del
destilado a 49ºC
(120ºF)
PD<365psia
(2.52MPa)
Utilizar
condensador
parcial
c. total + agua
Pb
Pb>215 psia
c. parcial
D
L0
x, y
PD>365psia
Elegir un refrigerante para
operar el condensador
parcial a 415 psia(2.86 MPa)
Estimar la presión de colas (PB)
59
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
D
PD<30 psia)
PD<365psia
(2.52MPa)
Utilizar
condensador
parcial
PD>365psia
Elegir un refrigerante para
operar el condensador
parcial a 415 psia(2.86 MPa)
P atmosférica o ligeramente superior.
Operación a vacío: P lo más alta posible
Operación a presión: P lo más baja posible
Comprobación de
la estabilidad de
las colas
Estimar la presión de colas (PB)
Calcular la T de
burbuja (TB) de
las colas a PB
Pcabeza = Pcondensador
∆PcondensadorD
TB<temperatura
de
descomposición
de colas o T
crítica
∆Pcolumna
Fin
B
Pcolas = Pcabeza + ∆Pcondensador + ∆Pcolumna
Ampliación Operaciones de Separación. 1. Métodos aproximados
57
TB>temperatura de
descomposición de colas
o T crítica
Disminuir
presión PD de
forma
aproximada
Ampliación Operaciones de Separación. 1. Métodos aproximados
60
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Métodos aproximados para el cálculo de
columnas de rectificación
multicomponente: método FUG
• Número mínimo de etapas de
equilibrio: ecuación de Fenske
• Distribución de componentes NK a
reflujo total
Underwood (clase 1)
• Reflujo mínimo
Colburn
• Número de etapas teóricas (Gilliland)
Colburn “riguroso”
Underwood (clase 2)
Igualdad de fracciones molares entre las etapas
los flujos de vapor y líquido varían de una etapa a otra
y iN = K iN x i,N
y iN = x iN −1
x i,N −1 = K iN x i,N
y i,N −1 = K i,N −1 x i,N −1 = K iNK i,N −1 x i,N
y i,1 = K i,NK i,N−1 ...K i,2K i,1 x i,N
x i,0 x j,N Nmin
=
α
x x ∏ k
i,N j,0 k =1
x
y i,1
= αNαN−1 ...α2α1 iN
x jN
y j,1
Gilliland
• Piso de alimentación
Número mínimo de etapas de equilibrio: ecuación de Fenske
• Estimación preliminar de costes
0 = condensador
61
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Método FUG
64
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Número mínimo de etapas de equilibrio: ecuación de Fenske
Especificar
alimentación
y iN = K iN x i,N
Especificar la separación
de dos componentes
clave
x i,N −1 = K iN x i,N
y iN = x iN −1
y i,N −1 = K i,N −1 x i,N −1 = K iNK i,N −1 x i,N
Estimar la
separación de los
componentes no
clave
x i,N − 2 = K iNK i,N −1 x i,N
y iN −1 = x iN − 2
y i,N − 2 = K i,N − 2 x i,N − 2 = K i,NK i,N −1K i,N − 2 x i,N
Determinar la P de la
columna y el tipo de
condensador
(cálculos de los
puntos de burbuja y
de rocío)
y iN − 2 = x iN − 3
62
Ampliación Operaciones de Separación. 1. Métodos aproximados
x i,N − 3 = K iNK i,N −1K i,N − 2 x i,N
…
y i,1 = K i,NK i,N−1...K i,2K i,1 x i,N
Ampliación Operaciones de Separación. 1. Métodos aproximados
65
de rocío)
Universitat d’Alacant
Universidad de Alicante
Aplicar flash a la
alimentación para la
presión de la columna
(flash adiabático)
Número mínimo de etapas de equilibrio: ecuación de Fenske
Cálculo de la relación
de reflujo mínima
(correlación de
Underwood)
Cálculo del Nº
mínimo de etapas
teóricas (ec. de
Fenske)
y i,1 = K i,NK i,N−1...K i,2K i,1 x i,N
y j,1 = K j,NK j,N−1...K j,2K j,1x j,N
Cálculo del número de etapas
teóricas para la relación de refujo
especificada > valor mínimo
(correlación de Gilliland)
Cálculo de la
separación de los
componentes no
clave (ec. de Fenske)
Separación
estimada =
Separación
calculada
Universitat d’Alacant
Universidad de Alicante
1
αi, nº de etapa =
Localización de la
etapa de alimentación
(ec. de Kirkbride)
Si etapa 0 = condensador:
x
y i,1
= αNαN−1 ...α2α1 iN
x jN
y j,1
K i, nº de etapa
K j, nº de etapa
y i1 = x i0
x i,0 x j,N Nmin
=
α
x x ∏ k
i,N j,0 k =1
No
Cálculo de los servicios del
condensador y de la
caldera (balances de
energía)
Si
1
Ampliación Operaciones de Separación. 1. Métodos aproximados
Fin
63
Ampliación Operaciones de Separación. 1. Métodos aproximados
66
Universitat d’Alacant
Universidad de Alicante
x i ,0 x j, N N min
=
αk
x x k∏
=1
i, N j,0
Universitat d’Alacant
Universidad de Alicante
volatilidad
relativa
constante
i = LK y j = HK
Nmín influenciado por los
componentes no clave
solamente debido a su
efecto sobre el valor de
la volatilidad relativa de
los componentes clave
Cálculo del reflujo mínimo
x i, 0 x j, N
= α N min
x x
i , N j,0
N min
Condensador total: no
incluido en N
xziD x j, N
log i,0
,0
x i, N xzjjD
=
log(αij ) m
• Sistemas de clase 1
1 punto de contacto
• Sistemas de Clase 2
Más de 1 punto de contacto
A, B, C
d b j
log i
d j b i
=
log α m
N min
(( ) ( α ) )
α m = α ij
N
1
A, B, C, D A, B, C, D
2
B, C, D
ij 1
Condensador parcial:
incluido en N
Ampliación Operaciones de Separación. 1. Métodos aproximados
67
log α m
(( ) ( ) )
α m = α ij
N
α ij
1
B, C, D
70
Universitat d’Alacant
Universidad de Alicante
Ecuación de Underwood para separaciones
de clase 1
Distribución de componentes NK a reflujo total
N min =
Zona para
eliminar D
Zona para
eliminar A
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
d b j
log i
d j b i
A, B, C
ecuación de Fenske
di d r
N min
= (α i,r )m
bi b r
bi =
y i∞ = K i∞ x i∞
fi
d
N
1 + r (α ir )mmin
br
d
f i r (α ir )mN min
b
di = r
d
1 + r (α ir )mN min
br
Ampliación Operaciones de Separación. 1. Métodos aproximados
xLK ,D
xHK ,D
− α LK ,HK F
x HK ,F
(L ∞ )min = x LK ,F
(L ∞ )min =
68
Ampliación Operaciones de Separación. 1. Métodos aproximados
F
:
(
)
(αLK ,HK )F − 1
Ampliación Operaciones de Separación. 1. Métodos aproximados
71
Universitat d’Alacant
Universidad de Alicante
Distribución de componentes a Rmín
L F DxLK ,D
Dx HK ,D
− α LK ,HK F
F L F x LK ,F
L F x HK ,F
LF Dx i,D
DxHK ,D
,HK F − 1− αi,HK F
F
αLK
F LF xi,F
LF xHK ,F
L ∞ min
L F Dx=i,D
DxHK ,D
FF L x − αi,HK F Lαxi,HK F − 1
L ∞ min
F HK ,F
F i,F
=
F
α i,HK F − 1
(
(L ∞ )min =
( )
1 punto de
contacto
(
Dx i,D
69
Dx iD
L F x iF
=
(
)
(
( )
Más de 1 punto de
contacto
)
(
LF xi,F
• Hay componentes no
repartidos
D
L F DxLK ,D
Dx HK ,D
− αLK ,HK F
F LF x LK ,F
L F x HK ,F
F
• Sistemas de clase 1
• Sistemas de Clase 2
(
)
(αLK ,HK )F − 1
o, multiplica ndo por
Haciendo i = LK y j = HK
Cálculo del reflujo mínimo
• Mezclas con todos los
componentes repartidos
D
Considerando xi∞ = xiF
Universitat d’Alacant
Universidad de Alicante
• Mezclas binarias
( )
( )∞
V∞ = L ∞ + D
fi = di + bi
1
x i ,D
x jD
− α ij
∞ x
L ∞ x i∞
j∞
=
D
α ij − 1
y i∞ V∞ = x i∞ L ∞ + x iD D
2
)
(
)
)
LF DxLK ,D
DxHK ,D
− αLK ,HK F
F LF xLK ,F
LF xHK ,F
=
αLK ,HK F − 1
(
(
)
)
)
(αi,HK )F − 1 DxLK ,D
Dx HK ,D
DxHK ,D
(αLK ,HK )F − 1 LF xLK ,F − (αLK ,HK )F LF xHK ,F + (αi,HK )F LF xHK ,F
(
)
αi,HK − 1 Dx
F
LK ,D +
=
αLK ,HK F − 1 L F x LK ,F
(
)
(
) (
)
)
αLK,HK − αi,HK Dx
HK ,D
F
F
αLK,HK F − 1
L F x HK ,F
(
Ampliación Operaciones de Separación. 1. Métodos aproximados
72
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Relación de reflujo externo
Razón de reflujo
externa: Lext/D
D
D
(
)
reordenar
)
(VL∞∞H+V∞D)+H(VL∞min
+ )(externo
L min ) externo
HL = H
(LLmin
= )(externo
L min ) externo
+ D H V+ D
+ LH∞VH+L∞L ∞HL∞
αi∞Dx iD
L∞
V∞ = ∑ V∞ y i∞ = ∑
V∞H = L) ∞+ D
+ (DH − H ) = (L )
L ∞ (H V∞ −
L∞
V∞
V
min externo (H V − HL )
= (R min ) externo =
L∞
V∞ y i∞ 1 −
= Dx iD
V∞ α i∞k HK∞
L∞
V∞
L∞
(
i α i∞ −
i
(L ∞ )min (H V∞ − HL∞ ) + D(HV∞ − HV )
D(H V − HL )
φ
73
Ampliación Operaciones de Separación. 1. Métodos aproximados
V∞ y i∞ =
α i∞Dx iD
L∞
α i∞ −
V∞k HK∞
V∞k HK ∞
Sumatorio para todos los componentes
presentes en el vapor
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
76
Universitat d’Alacant
Universidad de Alicante
Ecuación de Underwood ¡OJO!
para separaciones
Se está definiendo la
de clase 2
razón de reflujo interno como
(α ) x
α Dx
V∞ = ∑ V∞ y i∞ = ∑ i∞ iD
αi∞ − Φ
i
i
Enriquecimiento
L∞/D (igual al externo)
Sector de
enriquecimiento
∑ (α ir ) ∞ −iDφ = 1 + (R ∞ )mín
Sector de agotamiento
(α ' ) x
∑ (α' ir ) ∞ −iBφ' = 1 − (R '∞ )mín
ir ∞
1 + (R∞)min = 1 + L∞/D = (D + L∞)/D = V∞/D
ir ∞
Aná
Análogamente
(α ) x
∑ (αirir )∞∞ −iDφ = 1 + (R ∞ )min
Agotamiento
•
R∞ = L∞/D y R’∞ = L’∞/B
•
Se suponen constantes las volatilidades relativas en la
sección entre las dos zonas de contacto
•
αi=ki/kHK
(L mín ) externo
(L mín ) externo
V∞
D
equilibrio
V∞yi∞ = (L∞/ki∞)yi∞ + DxiD
Razón de reflujo
interna: Lint/V
(L min ) externo
V∞yi∞ = L∞xi∞ + DxiD
(L mín )externo + D
(L mín ) externo + D
− V∞' =
i
Se supone que (R∞)min y (R’∞)min están relacionadas por la
suposición de flujo molar constante (L' ) − (L ) = ψF
∞ min
74
(α' ) x
∑ (α' ir ) ∞ −iBφ' = 1 − (R'∞ )min
L' ∞
ir ∞
V∞' k 'HK∞
77
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
La raíz común, θ = φ = φ‘:
α'i∞ −
Φ’
∞
Ampliación Operaciones de Separación. 1. Métodos aproximados
α 'i∞ Bx iB
∑
Universitat d’Alacant
Universidad de Alicante
(α ) z
∑ (α ir) ∞ −iFθ = 1 − ψ
Ecuación de Underwood para separaciones
de clase 2: raíz común
ir ∞
ψ da la condición térmica de la alimentación
r se toma como el clave pesado, HK
(α ) x
∑ (αirir )∞∞ −iDφ = 1 + (R∞ )min
(α' ) x
Cuando
solamente
se
distribuyen
componentes clave: una raíz θ, αLK,HK>θ>1.
Cuando hay distribución de algún componente no
clave: m raíces de θ, siendo m el número de
componentes distribuidos menos 1, cada θ está
comprendida entre una pareja adyacente de
volatilidades
relativas
de
componentes
distribuidos.
Ampliación Operaciones de Separación. 1. Métodos aproximados
∑ (α'irir )∞∞ −iBφ' = 1 − (R'∞ )min
dos
75
?
(α ) d
∑ (αirir)∞∞− iφ = D + L ∞ = V∞
xD
xB
(α' ) b
∑ (α'irir)∞∞− iφ' = B − L'∞ = − V '∞
(α ) d
(α ) b
∑ (αirir)∞∞− iφ + (αirir)∞∞− iφ = V∞ − V'∞
(α ) z
∑ (α ir) ∞ −iFθ = 1 − ψ
ir ∞
(α ) f
∑ (αirir)∞∞−iφ = (1 − Ψ ) ⋅ F
Ampliación Operaciones de Separación. 1. Métodos aproximados
78
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Ecuación de Underwood para separaciones
de clase 2: raíz común
(α ) x
∑ (αirir )∞∞ −iDφ = 1 + (R∞ )min
(α' ) x
∑ (α'irir )∞∞ −iBφ' = 1 − (R'∞ )min
Ecuación de Underwood para separaciones
de clase 2: raíz común
L∞ '
L∞
FziF = V∞ ' y i∞ '
− 1 − V∞ y i∞
− 1
V∞ ' k i∞ '
V∞k i∞
Al buscar la raíz
común, se está
considerando que
L∞
φ’= θ
φ =θ
L∞ '
y
V∞k HK∞
L∞'
L∞
FziF = V∞ ' y i∞ '
− 1 − V∞ y i∞
− 1
V∞ ' α i∞ ' k HK∞ '
V∞ αi∞k HK∞
V∞ ' k HK∞ '
son iguales
θ
θ
− 1 − V∞ y i∞
− 1
FziF = V∞ ' y i∞ '
α i∞ '
α i∞
iguales
θ
θ
FziF = V∞ ' y i∞ '
− 1 − V∞ y i∞
− 1 = V∞ ' y i∞ '− V∞ y i∞
α i∞
α i∞
(
79
Ampliación Operaciones de Separación. 1. Métodos aproximados
i∞
82
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Ecuación de Underwood para separaciones
de clase 2: raíz común
Al obtener la raíz a
partir de la ecuación
(α ) z
) θ −α αi∞
∑ (α ir) ∞ −iFθ = 1 − ψ
Ecuación de Underwood para separaciones
de clase 2: raíz común
Se está considerando que
L∞
L∞ '
y
V∞k HK∞
V∞ ' k HK∞ '
θ − α i∞
FziF = V∞ ' y i∞ '− V∞ y i∞
α i∞
(1 − ψ )FyF
(
α i∞ ziF
= (1 − ψ ) yF
θ − α i∞
)
sumando
son iguales
ir ∞
(diapositiva anterior)
(α ) z
∑ (α ir) ∞ −iFθ = 1 − ψ
ir ∞
Se está considerando que
(αir )∞ y (α ir ' ) ∞
son iguales
(diapositivas posteriores)
80
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Ecuación de Underwood para separaciones
de clase 2: raíz común
V∞
L∞
V ∞’
L∞’
Ecuación de Underwood ¡OJO!
para separaciones
Se está definiendo la
de clase 2
razón de reflujo interno como
FziF + V∞ ' y i∞ '+L ∞ x i∞ = V∞ y i∞ + L ∞ ' x i∞ '
FziF + V∞ ' y i∞ '+L ∞
F
83
Ampliación Operaciones de Separación. 1. Métodos aproximados
y i∞
y i∞ '
= V∞ y i∞ + L ∞ '
k i∞
k i∞ '
L∞'
L∞
FziF = y i∞ '
− V∞ ' − y i∞
− V∞
k i∞ '
k i∞
L∞ '
L∞
FziF = V∞ ' y i∞ '
− 1 − V∞ y i∞
− 1
V∞ ' k i∞ '
V∞k i∞
Sector de
enriquecimiento
Sector de agotamiento
L∞/D (igual al externo)
(αir ) ∞ x iD
∑ (α ) − φ = 1 + (R ∞ )mín
ir ∞
(α'ir ) ∞ x iB
∑ (α' ) − φ' = 1 − (R '∞ )mín
ir ∞
•
R∞ = L∞/D y R’∞ = L’∞/B
•
Se suponen constantes las volatilidades relativas en la
sección entre las dos zonas de contacto
•
Se supone que (R∞)min y (R’∞)min están relacionadas por la
suposición de flujo molar constante (L' ) − (L ) = ψF
∞ min
Ampliación Operaciones de Separación. 1. Métodos aproximados
81
Ampliación Operaciones de Separación. 1. Métodos aproximados
∞
84
Universitat d’Alacant
Universidad de Alicante
La raíz común, θ = φ = φ‘:
Universitat d’Alacant
Universidad de Alicante
La composición del punto de contacto en el
sector de enriquecimiento
(α ) z
∑ (α ir) ∞ −iFθ = 1 − ψ
ir ∞
V α k
D
x
x i∞ ∞ i∞ KH∞ − 1 =
x iD = iD
L∞
R∞
L∞
ψ da la condición térmica de la alimentación
r se toma como el clave pesado, HK
Cuando
solamente
se
distribuyen
componentes clave: una raíz θ, αLK,HK>θ>1.
dos
Cuando hay distribución de algún componente no ?
clave: m raíces de θ, siendo m el número de
componentes distribuidos menos 1, cada θ está
comprendida entre una pareja adyacente de
volatilidades
relativas
de
componentes
distribuidos.
85
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
x i∞ =
x iD
V α k
R ∞ ∞ i∞ KH∞ − 1
L∞
⋅
L∞
V∞k KH∞
L∞
V∞k KH∞
x i∞ =
θ
θx iD
( R ∞ )min [( α ir )∞ − θ]
88
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Cuando solamente se distribuyen dos componentes clave:
raíz θ, αLK,HK>θ>1.
La composición del punto de contacto en el
→ Se busca una solució
solución
sector de enriquecimiento
una
entre 0 y 1 → que haga que l <
Cuando hay distribución de algún componente no clave: m raíces
de θ, siendo m el número de componentes distribuidos menos 1,
cada θ está comprendida entre una pareja adyacente de
volatilidades relativas de componentes distribuidos.
x i∞
?
v (ya que l=(L/(KV)v), que es
θx iD
una condició
condición razonable en
=
este sector
( R ∞ )min [( α ir )∞ − θ]
Se está obteniendo soluciones para L/(KHKV) en una zona que
incluye el piso de alimentación.
θ es la raíz de que cumple (αHNK,r)∞ > θ > 0
Se verá más adelante (Hengstebeck) que si la separación es
buena, KHK ≈ L/V y KLK ≈ L’/V’.
HNK se refiere al no clave pesado en el destilado
para reflujo mínimo.
Al buscar soluciones entre αLK,HK y 1: ¡Se está obteniendo un valor
comprendido entre KLK/KHK y KHK/KHK, es decir entre L’/(KHKV’) y
L/(KHKV)!
Esta raíz es igual al factor de absorción.
Si hay más componentes distribuidos además de los claves, a cada
par de componentes distribuidos se le da el mismo tratamiento
que a los clave.
Ampliación Operaciones de Separación. 1. Métodos aproximados
86
Universitat d’Alacant
Universidad de Alicante
Ampliación Operaciones de Separación. 1. Métodos aproximados
89
Universitat d’Alacant
Universidad de Alicante
La composición del punto de contacto en el
sector de enriquecimiento
x i∞ =
¡Ojo! Para la obtención de las raices se utiliza la ec. de Underwood
para el sector de enriquecimiento!!!, que es no es más que otra
forma de expresar la ecuación anterior (ambas proceden del mismo
balance de materia + equilibrio)
La composición del punto de contacto en el
sector de agotamiento
θx iD
( R ∞ )min [( α ir )∞ − θ]
x'i∞ =
θx iB
[( R'∞ )min + 1][( α ir )∞ − θ]
Balance de materia
V∞yi∞ = L∞xi∞ + DxiD
V∞αi∞kHK∞xi∞ = L∞xi∞ + DxiD
HNK es el no clave más pesado en el producto de
colas para reflujo mínimo.
xi∞(V∞αi∞kHK∞-L∞) = DxiD
V α k
D
x
x i∞ ∞ i∞ KH∞ − 1 =
x iD = iD
L∞
R∞
L∞
Ampliación Operaciones de Separación. 1. Métodos aproximados
(αHNK,r)∞ > θ > 0
87
¡Ojo! Para la obtención de las raices se utiliza la ec. de
Underwood para el sector de agotamiento!!!, que es no es más
que otra forma de expresar la ecuación anterior (ambas
proceden del mismo balance de materia + equilibrio)
Ampliación Operaciones de Separación. 1. Métodos aproximados
90
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Método de Gilliland
Aproximación de Colburn para la
composición en la zona de contacto
x LK∞ =
rF
(1 + rA )(1 + ∑ α i , HK x Fi )
x HK∞ =
x LK∞
• Puede calcularse la razón mínima de reflujo mediante
una sola ecuación
• Utiliza un valor medio de las volatilidades relativas
(R ∞ ) min + 1 = a ( b + c + d )
rF
Σ1: ΗΗΚ
rF es la relación estimada entre las concentraciones de LK y
HK en el piso de alimentación, considerada igual al valor de
esta relación en el alimento.
x
x
x
a = D ,LK F,HK − D,HK
x
x
x
B,HK
B,HK F,LK
c=∑
El sumatorio se refiere a todos los componentes de la parte
líquida del alimento más pesados que el componente pesado.
x
b = 1 + α c F,LK
x
F,HK
d=
αi,HK se calcula a la temperatura de ebullición del alimento
Ampliación Operaciones de Separación. 1. Métodos aproximados
91
Universitat d’Alacant
Universidad de Alicante
x B,HK
α −1
c
1
α i x Bi
α c − αi
Σ2: LLK
α: con respecto
a HK a la
temperatura de
ebullición del
alimento
D α i x Di
∑
R 2 αi −1
94
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Método de Colburn
Número de etapas teóricas
A reflujo mínimo las dos funciones siguientes han de ser iguales:
ψ 1 = rm / rn
ψ2 =
Separaciones que requieren gran número de
etapas: R/Rmín aproximadamente 1.10
1
(1 − ∑ b m α mHK x m )(1 − ∑ b n x n )
• m se refiere a la zona inaccesible de agotamiento y n a la de enriquecimiento.
• rm y rn son las relaciones entre las concentraciones de LK y HK en las zonas
inaccesibles de agotamiento y enriquecimiento, respectivamente.
∑
•
b mα mHK x m se considera para todos los componentes más pesados que HK en la
zona inaccesible de agotamiento
•
b n x n se refiere a todos los componentes más ligeros que LK en la zona inaccesible
de enriquecimiento
∑
Separaciones que requieren
R/Rmin aproximadamente 1.50
pocas
etapas:
Casos intermedios: R/Rmín = 1.30.
N = N{Nmin {x iD , x iB , α}, R min {ziF , x iD , ψ, α}, R}
• bm y bn son factores que dependen de la volatilidad relativa, y se encuentran en la
bibliografía.
αmHK es la volatilidad relativa con respecto a HK
Ampliación Operaciones de Separación. 1. Métodos aproximados
92
Universitat d’Alacant
Universidad de Alicante
95
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
La razón de reflujo para la cual ψ1 = ψ2 se obtiene por
tanteos, mediante el procedimiento siguiente:
1) Nº de componentes = 4 - 11
2) ψ = 0.28 - 1.42
3) Presión = vacío - 600 psia
a) Se calcula una razón de reflujo mínima por un
método aproximado.
4) α = 1.1. -4.05
b) Con éste valor se calculan, mediante la ec. de
Fenske-Underwood, las concentraciones inaccesibles en
las zonas de enriquecimiento y agotamiento para todos
los componentes.
6) Nmín = 3.4 -60.3
c) Se determinan ψ1 y ψ2. Si ψ1 > ψ2, la razón de reflujo
elegida fue demasiado grande, si ψ1 < ψ2, la razón de
reflujo elegida fue demasiado pequeña.
Ampliación Operaciones de Separación. 1. Métodos aproximados
93
5) Rmín = 0.53 - 9.09
Molokanov y col.:
N − N min
1 + 54.4 X X − 1
Y=
= 1 − exp
0.5
N +1
11 + 117.2 X X
Ampliación Operaciones de Separación. 1. Métodos aproximados
X=
R − R min
R +1
96
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Localización de la etapa de alimentación
N R z HK ,F z LK ,B
=
N S z LK ,F z HK,D
N min ,s =
Ss =
ln Ss
ln α s
z LK x B,HK
z HK x B,LK
NS
N
=
N min ,s N min
2
B
D
0.206
Ecuación de Kirkbride
αs es la
volatilidad
relativa media
de LK en la
sección
inferior de la
Ecuación de Fenske columna
97
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
100
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Estimación preliminar de costes
Para encontrar la R más económica, sólo se necesita tener
en cuenta los elementos de coste que dependen de R. En
los costes de funcionamiento se incluyen:
• calor a suministrar en la caldera
Métodos gráficos
• Diagramas de Hengstebeck
• Razón ente claves
• agua para el condensador
• Gráficos d/b
• costes de bombeo
Para obtener el coste de capital necesario para construir
la planta se estima primero el coste del equipo principal en
función de R. Con ello queda impuesto el coste de columna
y de los cambiadores de calor.
98
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Coste del equipo principal
Montaje
Tuberías y válvulas
Instrumentos
Material eléctrico
Soportes mecánicos
Pintura, aislamiento térmico, etc.
Diseño
Costes asociados ajenos a la producción
Imprevistos
Ampliación Operaciones de Separación. 1. Métodos aproximados
101
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Diagrama de Hengstebeck
100
30
35
10
5
15
5
200
xe,LK = xLK/(xLK + xHK)
ye,LK = yLK/(yLK + yHK)
Composiciones y
caudales efectivos
Le = L(xLK + xHK)
Ve = V(yLK + yHK)
• Composiciones
limitantes de los
componentes no clave
20
40
20
280
Ver perfiles
de la columna
99
Ampliación Operaciones de Separación. 1. Métodos aproximados
x HNK,lim =
x LNK ,lim
x HNK,B (B / L' )
1.0 − K HNK / K LK
y LNK ,D ( D / L)
=
K LNK / K HK − 1.0
y HNK ,lim =
y LNK , lim =
x HNK ,B (B / V ' )
K LK / K HNK − 1.0
y LNK , D ( D / V)
1.0 − K HK / K LNK
102
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Diagrama de Hengstebeck
• Composiciones
limitantes de los
Separación pronunciada
componentes no clave
Construcción del diagrama:
yHNK,lim =
xHNK,B (B / V ' )
K LK / K HNK − 1.0
Zona de HNK constante
1. Determinar la razón de reflujo
2. Determinar los caudales de vapor y de líquido
Balance:
xHNK,lim L’ = yHNK, lim V’ + xHNK, B B
xLK,B<<< xLK
3. calcular las composiciones limitantes de los no clave
Equilibrio:
yHNK,lim
xLK,BB + xLKL’
= yLK=V’KHNK, lim xHNK, limL'
4. Determinar αLK,HK a varios valores de xe en cada
sector, mediante cálculos del punto de burbuja,
utilizando las composiciones limitantes de los no clave
xLKL’ ≈ yLKV’ xHNK,B B
V'
HNK
,lim
KLK y=
yLK
/x=LK ≈LL’/V’
'
−1
V ' K HNK
K LK =
V'
L'
yHNK,lim
− V' = xHNK,B B
K HNK
103
Ampliación Operaciones de Separación. 1. Métodos aproximados
x e, LK =
x LK
10
. − ∑ x LNK, lim
Universitat d’Alacant
Universidad de Alicante
zona de xHNK constante
del sector de
agotamiento
x e, LK =
x LK
10
. − ∑ x HNK , lim
( ∑ xHNK,lim ) − L(1 − ∑ xLNK,lim )
F
L' − L e L' 1 −
ψ e = Le = e
=
Fe
Fe
y LK
y e, LK =
10
. − ∑ y LNK, lim
y LK
y e, LK =
1.0 − ∑ y HNK , lim
L e = L(10
. − ∑ x LNK, lim )
L e ' = L' (10
. − ∑ x HNK, lim )
Ve = V(10
. − ∑ y LNK, lim )
Ve ' = V' (1.0 − ∑ y HNK, lim )
ψe =
ψe =
104
Ampliación Operaciones de Separación. 1. Métodos aproximados
Fe
∑ xLNK,lim − L' ∑ xHNK,lim
Fe
FL + L
∑ xLNK,lim − L' ∑ xHNK,lim
Fe
107
Universitat d’Alacant
Universidad de Alicante
Construcción de la curva de equilibrio:
Representación gráfica de la razón entre claves
Suponer valores de composiciones en cada sector y hacer
cálculos de equilibrio
Punto de burbuja
L´−L + L
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
xLK, xHK, xHNKi, lim, xLNKi, lim
106
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
zona de xLNK constante
del sector de
enriquecimiento
5. Representar los puntos (xe, ye)
xe
yLK, yHK, yHNKi, lim, yLNKi, lim
ye
Suponer valores de composiciones en cada sector y utilizar
la expresión de y= f(x) para mezclas binarias utilizando la
volatilidad
xLK, xHK, xHNKi, lim, xLNKi, lim
xe
yLK =
αx LK
1 + ( α − 1)xLK
ye
α = KLK/KHK=(L'/V')/(L/V)
Ampliación Operaciones de Separación. 1. Métodos aproximados
105
Ampliación Operaciones de Separación. 1. Métodos aproximados
108
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Representación gráfica de la razón entre claves
La ecuación de Smoker se aplica individualmente a las
secciones de agotamiento y enriquecimiento.
Sector de enriquecimiento :
m = R/(R + 1) (pendiente de la operativa)
b = xD/(R + 1) (ordenada en el origen de la operativa)
xo = xD
xn = xint (fracción molar de la intersección operativa - recta q)
109
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
la distribución de componentes no clave a reflujo
total es de
una no
buena
aproximación
distribución que
Distribución
claves:
gráficosa la
d/b
se obtendrá con la columna trabajando a una razón de
reflujo finita.
Aplicación para determinar la
distribución de componentes NK:
•Se reescribe la ec. de Fenske
log (di/bi) = A + C log αi
•Se determinan A y C a partir de las
especificaciones de LK y HK.
•Se lee log (di/bi) correspondiente a la
componente
d b j
αi para cada
NK sobre la
log i
d j bi
recta Nobtenida.
=
min
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
x o ' 1 − mc(α − 1) x n ' /( α − mc 2
x n ' 1 − mc(α − 1) x o ' /( α − mc 2
N=
log α /( mc 2 )
xo '= xo − k
xn '= xn − k
Sector de agotamiento:
L'
R + ψ + ψ(B / D)
=
V' R + ψ − (1 − ψ)(B / D)
(z − x D ) x B
b=
(R + 1)z + (ψ − 1) x D − (R + ψ) x B
m=
x o = x int
xn = xB
Ampliación Operaciones de Separación. 1. Métodos aproximados
Jafarey:
• Volatilidad relativa constante (útil si es próxima a 1)
• Flujos molares constantes
• etano-etileno e isobutano-butano
c = 1 + (α − 1) k
Universitat d’Alacant
Universidad de Alicante
113
Universitat d’Alacant
Universidad de Alicante
Solución analítica del diagrama x-y:
Ecuación de Smoker
{ [
{ [
112
log αm
(equivale a aplicar la ec. de Fenske,
como se vió
vió en el apartado 4.1) 110
log
Ampliación Operaciones de Separación. 1. Métodos aproximados
[
]
ln S
R+ψ
lnα 1 −
(
R
+
1
)(
Rz
+
ψ
)
x
S = LK
x HK
]}
]}
K, (0 < k < 1) :
m(α - 1)k2 + [m + b (α - 1) - α]k + b = 0
Ampliación Operaciones de Separación. 1. Métodos aproximados
N=
111
xHK
D xLK
B
• Se calcula N para la operación normal de la columna
• Se resuelven los balances para las nuevas condiciones de
operación
• Se recalcula el nuevo valor de la variable bajo control de
forma que N se mantenga
Ampliación Operaciones de Separación. 1. Métodos aproximados
114
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Análisis de columnas existentes:
método de Smith-Brinkley
fi =
(1 − S n ,i N − M ) + R(1 − S n ,i )
(1 − S n ,i N − M ) + R (1 − S n ,i ) + h i S n ,i N − M (1 − S m,i M +1 )
Bx
fi = B
Fz i
V
L
V'
= Ki '
L'
K i ' L (1 − S n ,i )
OBSERVACIONES
• Los criterios 1 y 2 suelen funcionar bien, pero no
siempre (→ Rmín)
Dados N, M y
R, calcula la
composición
de los
productos
• Los LNK tienden a amentar la razón entre claves
óptima en el piso de alimentación, mientras que los
HNK tienden a disminuirla. Los criterios 1 y 2
pueden fallar cuando LNK/HNK difieren mucho de 1
S n ,i = K i
(sector de enriquecimiento)
S m ,i
(sector de agotamiento)
N: número de
pisos
• Los NK cuya volatilidad es próxima a la de los claves
tienden a aumentar la razón óptima xLK/xHK en el
piso de alimentación
(alimento predominante liquido)
M: número de
pisos por
debajo del
alimento.
• El primer criterio suele funcionar mejor cuando hay
más LNK que HNK, mientras que el segundo lo hace
cuando HNK es superior a LNK.
hi =
K i L' (1 − S m ,i )
L (1 − S n ,i )
hi =
L' (1 − S m ,i )
(alimento predominante vapor)
Ampliación Operaciones de Separación. 1. Métodos aproximados
115
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Utilidad de los métodos gráficos
Posición óptima del piso de alimentación
• xLK/xHK → relación en la porción líquida del
alimento
1. La detección de pinch zones
2. La identificación de puntos de alimentación
inadecuados
• Intersección entre las rectas operativas en un
diagrama de Hengstebeck.
3. La identificación de excesivos reflujo y/o vapor
generado en la caldera
• Pendientes más parecidas a ambos lados del
piso de alimentación en una representación de
la razón de claves
4. Detectar cuando resultan adecuados
intercambiadores interetapas
• Obtenido mediante cualquier técnica analítica
aproximada o rigurosa
Ampliación Operaciones de Separación. 1. Métodos aproximados
118
Ampliación Operaciones de Separación. 1. Métodos aproximados
5. Proporcionar orientación para la optimización de
la columna
116
Universitat d’Alacant
Universidad de Alicante
Ampliación Operaciones de Separación. 1. Métodos aproximados
119
Universitat d’Alacant
Universidad de Alicante
Posición óptima del piso de alimentación
Métodos de grupo: aplicación a
absorción
Procedimiento propuesto por Ricker y Greens :
1. Se suponen valores para NR y Ns
2. Se calcula la columna por un método riguroso y se determina la
razón de reflujo para obtener la separación deseada.
3. Con la razón de reflujo, se obtiene el número de pisos mediante un
método aproximado.
4. Con los resultados del paso anterior, se realiza una nueva
estimación de NR y Ns.
• Kremser ; Souders y Brown ;
Franklin ; Edmister.
Horton y
• N etapas adiabáticas; las especies presentes en
el vapor que entra están ausentes en el líquido
que entra ; Las etapas se numeran de cabeza a
cola.
5. Se comprueban las diferencias entre NR y Ns supuestos y
calculados.
Ampliación Operaciones de Separación. 1. Métodos aproximados
117
Ampliación Operaciones de Separación. 1. Métodos aproximados
120
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
yN = K NxN
φA =
LN VN yN = K N xNLN VN
1
A 1A 2 A 3 ... A N + A 2 A 3 ... A N + A 3 ... A N +...+ A N + 1
LNv N = K N VNlN
vN =
A=
lN
LN
K V
N N
l
vN = N
AN
1
K V
SN =
= N N
AN
LN
v
lN = N
SN
v N = lNSN
lN = v NA N
L
KV
121
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
lN = vNAN
L0
φA =
φA =
1
N
Ae + Ae
N −1
+ A e N − 2 +...+ A e + 1
Ae − 1
v1 = vN+1 φA
A e N +1 − 1
124
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Balance
vN = lN-1 + v1
lN = (lN-1 + v1)AN
Aná
Análogamente, para
el piso superior:
V1
lN-1 = (lN-2 + v1)AN-1
LN-1
VN
lN = lN-2 AN-1 AN + v1(AN + AN-1 AN)
LN
…
lN-2 = (lN-3 + v1)AN-2
VN+1
lN = v1(A1 A2 A3 ... AN + A2 A3 .... AN + A3 ... AN + ... + AN)
122
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
lN = v1(A1 A2 A3 ... AN + A2 A3 .... AN + A3 ... AN + ... + AN)
L0
V1
lN = vN+1 - v1
Balance
v1 = vN+1 φA
φA =
LN
VN
A 1A 2 A 3 ... A N
1
+ A 2 A 3 ... A N + A 3 ... A N +...+ A N + 1
VN+1
Ampliación Operaciones de Separación. 1. Métodos aproximados
Ecuaciones para un desorbedor:
l1 = lN+1 φS
vN+1 = v1(A1 A2 A3 ... AN + A2 A3 .... AN + A3 ... AN + ... + AN + 1)
LN-1
125
Ampliación Operaciones de Separación. 1. Métodos aproximados
φS =
Se − 1
Se N +1 − 1
KV 1
=
L
A
Balance total en el absorbedor para un componente
que aparece tanto en el vapor como en el líquido que
entran:
v1 = v N + 1φ A + l o (1 − φ S )
Fracció
Fracción no
absorbida del gas
de entrada
123
S=
Ampliación Operaciones de Separación. 1. Métodos aproximados
Fracció
Fracción
desorbida del
líquido de entrada
126
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
A e = [A N (A 1 + 1) + 0.25]
Se = [S1 (S N + 1) + 0.25]
1
2
1
2
TN − T1 VN +1 − V2
=
TN − To VN +1 − V1
Edmister
− 0.5
− 0.5
A1A 2 + A 2 + 1 = A 2e + A e + 1
1
1
=
A1A 2 + A 2 + 1 A 2e + A e + 1
Ae =
A 2e + A e − ( A1A 2 + A 2 ) = 0
− 1 ± 1 + 4( A1A 2 + A 2 )
2
=±
1
+ A1A 2 + A 2 − 0.5
4
A e = 0.25 + A 2 ( A1 + 1) − 0.5
127
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
1
V
N
V2 = V1 N +1
V1
Si To ≈ TN+1, (T1 - To) varía entre 0 y 20ºF, según la fracción
absorbida del gas que entra
aproximación de KREMSER :
L1 ≈ LN ≈ Lo, V1 ≈ VN ≈ VN+1 y T1 ≈ TN ≈ (To + TN+1)/2
(cuando sólo se absorbe una pequeña fracción del
gas de alimentación)
Universitat d’Alacant
Universidad de Alicante
Se supone un primer valor para LN, V1, TN y T1 (Aproximación de Kremser)
Aproximación: contracción
molar del vapor igual en todas
las etapas
Se calcula V2, L1, VN (aproximación de Horton y Franklin)
1
Balance de materia
N
V V
V
VN VN−1 VN − 2
V
⋅
⋅
⋅ ⋅ ⋅ 1 = 1 = 1 = N
VN+1 VN VN−1
V2 VN+1 V2
VN+1
130
Ampliación Operaciones de Separación. 1. Métodos aproximados
Horton y Franklin
V N
VN = VN+1 1
VN+1
L1 = L 0 + V2 − V1
T1 y TN
balance de entalpía
Absorbedor adiabá
adiabático, 2 etapas:
φA =
2 incógnitas
L0
V1
L1
V2
LN-1
VN
Se calcula K1, KN, A1, AN, S1, SN, Se, Ae, Φ A, Φ s:
se obtiene lN, v1 (es decir xN e y1)
se obtiene LN y V1
N
Balance de entalpía
Ecuación (TN, T1) = f(V1, V2, TN+1, To)
LN
VN+1
T1, TN
¿Diferencias entre valores calculados y supuestos despreciables?
NO
Ampliación Operaciones de Separación. 1. Métodos aproximados
128
Universitat d’Alacant
Universidad de Alicante
TN − T1 VN +1 − V2
=
TN − To VN +1 − V1
L0
V1
L1
V2
LN-1
VN
Ampliación Operaciones de Separación. 1. Métodos aproximados
131
Universitat d’Alacant
Universidad de Alicante
(variación de T del líquido proporcional
a V de gas absorbido)
El flujo mínimo de absorbente, que corresponde a un
número infinito de etapas :
(Lo)min = Kk VN+1 (1 - φAk)
VN+1 − V2 ↔ TN − T1
LN
SI
FIN
φA =
Ae − 1
A e N +1 − 1
0 (N = infinito, Ak<1)
L
A=
KV
VN+1 − V1 ↔ TN − T0
El subíndice K se refiere al componente clave
VN+1
Ak < 1
La fracción absorbida del gas de alimentación es pequeña
Ampliación Operaciones de Separación. 1. Métodos aproximados
129
Ampliación Operaciones de Separación. 1. Métodos aproximados
132
Universitat d’Alacant
Universidad de Alicante
Universitat d’Alacant
Universidad de Alicante
Para un desorbedor:
lN A o φSE + 1
=
−1
d
φ AE
Se = [SN(S1 + 1) + 0.25]1/2 - 0.5
L
L 2 = L1 N + 1
L1
1
L
L N = L N +1 1
L N +1
1
N
L N +1
(1 − φ Sk )
Kk
Ampliación Operaciones de Separación. 1. Métodos aproximados
dA 0
lN = dA 0 Φ S + lN − lNΦ A + d − dΦ A
lN = d( A 0 Φ S + 1) + lN − lNΦ A − dΦ A
lNΦ A = d( A 0 Φ S + 1) − dΦ A
lN + d
v M So φ AX + 1
=
−1
b
φSX
lM+1 S o φ AX + 1
=
φSX
b
133
1. Condensación parcial
AF =
1
A e = [A B ( A T + 1) + 0.25 ] 2 − 0.5
2. Cascada de absorción
3. Flash de la etapa de alimentación
5. Ebullición parcial
Ampliación Operaciones de Separación. 1. Métodos aproximados
134
Universitat d’Alacant
Universidad de Alicante
B y T: etapas de cola y
cabeza de cada
sección
LF y VF son las
corrientes que salen de
la etapa de alimentación
vN+1 = lN + d
Ao = Lo/(koD) (condensador parcial)
lN A o φSE + 1
=
−1
d
φ AE
Ao = Lo/D (condensador total)
D
v M So φ AX + 1
=
−1
b
φSX
ENRIQUECEDOR
137
Ampliación Operaciones de Separación. 1. Métodos aproximados
condensador
LN
− 0.5
LF
LF
l
=
= F
K F VF ( v FLF / VFlF ) VF v F
Universitat d’Alacant
Universidad de Alicante
Ampliación Operaciones de Separación. 1. Métodos aproximados
1
2
A o φSE + 1
b
φ AE
= AF
So φ AX + 1
d
φSX
4. Cascada de desorción
VN+1
136
Universitat d’Alacant
Universidad de Alicante
S e = [S T (SB + 1) + 0.25 ]
L0
• Subíndice X = agotador.
Ampliación Operaciones de Separación. 1. Métodos aproximados
Aplicación de los métodos de grupo a
cascadas complejas en contracorriente.
Método de grupo de Edmister
V1
• Numerado de cola a cabeza.
agotador
Universitat d’Alacant
Universidad de Alicante
lo =dAo
• Subíndice E = enriquecedor.
enriquecedor
lN = l0 Φ S + v N +1(1 − Φ A )
TN +1 − TN L N +1 − L N
=
TN + 1 − T1
L N + 1 − L1
v1 = lo + d
• Numerado de cabeza a cola.
N
V1 = Vo + L 2 − L1
( V o ) min =
v N+1 A o φSE + 1
=
d
φ AE
A o φSE + 1
b
φ AE
= AF
So φ AX + 1
d
φSX
A o φSE + 1
lN d
+
φ AE
d d =
v M b S o φ AX + 1
+
b
b
φSX
A o φSE + 1
lN + d
φ AE
d
=
v M + b S o φ AX + 1
b
φSX
vN+1: vapor que entra a E = vF
lM+1: líquido que entra a X = lF
A o φSE + 1
A o φSE + 1
φ AE
φ AE
b lF
=
= AF
So φ AX + 1
d v F So φ AX + 1
φSX
φSX
135
Ampliación Operaciones de Separación. 1. Métodos aproximados
138
Universitat d’Alacant
Universidad de Alicante
D
Enriquecedor
Numeración de
las etapas:
N
VF
Piso de alimentació
alimentación
Numeración de
las etapas:
V1E
L0E
VN+1,E
LNE
1
M
F VMX
LM+1,X
LF
1
Agotador
V0X
L1,X
B
139
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
Métodos de grupo: aplicación a
extracción líquido-líquido
K Di =
Ei =
Ui =
vi
yi
= V
li
xi
L
K Di V
L
1
L
=
E i K Di V
140
Ampliación Operaciones de Separación. 1. Métodos aproximados
Universitat d’Alacant
Universidad de Alicante
v1 = v n +1φ U + l o (1 − φ E )
l N = l o + v N+1 − v1
V
V2 = V1 N +1
V1
1
N
L1 = L o + V2 − V1
Ue − 1
N +1
Ue − 1
Ee − 1
φ E = N+1
Ee −1
φU =
V
VN = VN +1 1
VN +1
1
N
1
E e = [E1 (E N + 1) + 0.25] 2 − 0.5
1
U e = [U N ( U1 + 1) + 0.25] 2 − 0.5
• U se refiere a la transferencia desde la fase ligera a la fase pesada
• E se refiere a la transferencia desde la fase pesada a la fase ligera
• Las etapas se numeran de cabeza a cola
Ampliación Operaciones de Separación. 1. Métodos aproximados
141









