Cap´ıtulo 6 Programa
Anuncio

Capı́tulo 6
Programa
Introducción
Una pequeña descripción del programa es:
Especificar el tipo de aleación, el número de especies del átomo A = Cu, temperatura del sistema y el ciclo del cálculo.
Subrutina para hallar configuraciones al azar del sistema binario Ax Bx .
Subrutina que dada la configuración del sistema, obtiene la energı́a de dicho sistema considerando los potenciales ya mencionados.
Subrutina con el Método Montecarlo donde se realizan los promedios de energı́a
dentro de la población de las configuraciones aceptadas según el factor de Boltzman.
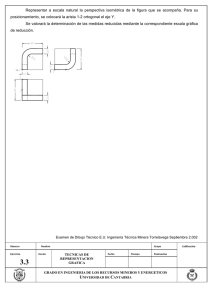
6.1.
Código y Diagrama de Flujo
#include <fstream.h>
#include<stdlib.h>
#include <iostream.h>
#include <math.h>
#include <stdio.h>
#define
#define
#define
#define
#define
IA
IM
AM
IQ
IR
16807
2147483647
(1.0/IM)
127773
2836
46
CAPÍTULO 6. PROGRAMA
47
#define MASK 123459876
void llenar(char *vector[]);
float ran0(long &idum);
void escoger(long &idum,char *vector[]);
void tipo();
void posicion();
void distancia();
void ultimo();
float energia();
void imprimir(char vectorarreglo[]);
void montecarlo(float temp,long &idum);
//#################### Variables Glosbales ####################################
int tip,
veces,
j=0,
cuenta=1,
bandera=0;
float arista,
vectorposicion[14][3],
distancias[14][14],
energiasub[14][14],
energiatotal,
temp,
sumaenergia=0,
energiag[1000000],
varianza=0,
nmax,
nmaxf,
energiainterna;
char vectorarreglo[14];
//#############################################################################
//##################### Main ##################################################
int main() {
long idum=1;
char *vector[14];
CAPÍTULO 6. PROGRAMA
48
int i,para=1,l;
tipo();
llenar(vector);
posicion();
distancia();
cout << "Energia Int
while(para==1){
Num acept
Varianza
Desviacion
Energia Max
energiainterna=0;
sumaenergia=0;
varianza=0;
cuenta=1;
//cout << "A que temperatura se encuentra el sistema (Grados Kelvin)? "<<endl;
cin >> temp;//Se establece la temperatura a la que se encuentra el sistema
//cout <<endl;
//cout << "Cual es el ciclo ?" <<endl;
cin >> veces;
//cout <<endl;
nmaxf=1000;
for(i=0;i <= veces; i++) {
escoger(idum,vector);//genera configuracion
energiatotal=0.5*energia();//Calculo de energia total
nmax=energiatotal;
if ( nmax <= nmaxf){
nmaxf=nmax;
}
montecarlo(temp,idum);
}
energiainterna=sumaenergia/(cuenta-1);
for(l=1;l<=(cuenta-1);l++){
varianza = varianza +(energiag[l]-energiainterna)*
(energiag[l]-energiainterna);
}
//###################### Calculo de Energia
cout << energiainterna << "
<< (1/cf)* varianza << "
Interna del Sistema ############
" << cuenta-1 << "
"
" << sqrt((1/cf)* varianza)
CAPÍTULO 6. PROGRAMA
49
<< "
" << nmaxf <<
"
";
ultimo();
cout << endl ;
cin >> para; //variable para aceptar iniciar un nuevo ciclo o no.
if (para==1){
varianza=0;
energiainterna=0;
cuenta=1;
}
getchar();
}//end while
return 0;
}//end main
//########################### Calcula numeros aleatorios #####################
float ran0(long &idum) {
long k;
float ans;
idum ^= MASK;
k = (idum)/IQ;
idum = IA*(idum-k*IQ) - IR*k;
if (idum < 0) idum += IM;
ans=AM*(idum);
idum ^= MASK;
return ans;
}//end ran0
//################## Tipo de aleacion y valor de la arista de la celda ########
void tipo() {
//cout << "Que tipo de aleacion es:" << endl;
//cout << "Cu-Cu=1; Cu-Pd=2 ;Pd-Pd=3 ; Cu-Pt=4; Pt-Pt=5." << endl;
cin >> tip;
switch(tip)//arista en Amstrongs
{
case 1:
{
CAPÍTULO 6. PROGRAMA
50
arista=3.61496;
}
break;
case 2:
{
arista=3.75238;
}
break;
case 3:
{
arista=3.8898;
}
break;
case 4:
{
arista=3.76903;
}
break;
case 5:
{
arista=3.9231;
}
break;
}
}//end tipo
//###################### Llenado con A y B un vector ##########################
void llenar(char *vector[]) {
int A,B;
int i;
//cout << "Cuantos atomos A hay? (Los atomos A son los del primer elemento
del tipo de aleacion escogida:" << endl;
cin >> A;
B = 14 - A;
for(i=0;i<A;i++){
vector[i] = "A";
}
for(i=A;i<=13;i++){
vector[i] = "B";
}
CAPÍTULO 6. PROGRAMA
51
}//end llenar
//########### Llenado de matriz con las posiciones de los atomos en la celda ##
void posicion() {
int i,j,k;
for(i=0;i<=13;i++){
for(j=0;j<=2;j++){
vectorposicion[i][j]=0;
}
} //cout<<endl;
vectorposicion[0][0]=0;//atomo 1
vectorposicion[0][1]=0;
vectorposicion[0][2]=0;
vectorposicion[1][0]=0;//atomo 2
vectorposicion[1][1]=0;
vectorposicion[1][2]=arista;
vectorposicion[2][0]=arista;//atomo 3
vectorposicion[2][1]=0;
vectorposicion[2][2]=0;
vectorposicion[3][0]=arista;//atomo 4
vectorposicion[3][1]=0;
vectorposicion[3][2]=arista;
vectorposicion[4][0]=arista/2;//atomo 5
vectorposicion[4][1]=0;
vectorposicion[4][2]=arista/2;
vectorposicion[5][0]=arista;//atomo 6
vectorposicion[5][1]=arista;
vectorposicion[5][2]=0;
vectorposicion[6][0]=arista;//atomo 7
vectorposicion[6][1]=arista/2;
vectorposicion[6][2]=arista/2;
vectorposicion[7][0]=arista;//atomo 8
CAPÍTULO 6. PROGRAMA
52
vectorposicion[7][1]=arista;
vectorposicion[7][2]=arista;
vectorposicion[8][0]=0;//atomo 9
vectorposicion[8][1]=arista;
vectorposicion[8][2]=arista;
vectorposicion[9][0]=0;//atomo 10
vectorposicion[9][1]=arista;
vectorposicion[9][2]=0;
vectorposicion[10][0]=arista/2;//atomo 11
vectorposicion[10][1]=arista;
vectorposicion[10][2]=arista/2;
vectorposicion[11][0]=arista/2;//atomo 12
vectorposicion[11][1]=arista/2;
vectorposicion[11][2]=arista;
vectorposicion[12][0]=0;//atomo 13
vectorposicion[12][1]=arista/2;
vectorposicion[12][2]=arista/2;
vectorposicion[13][0]=arista/2;//atomo 14
vectorposicion[13][1]=arista/2;
vectorposicion[13][2]=0;
}//end posicion
//############## Calculo de las distancias entre todos los atomos #############
void distancia() {
int i,j;
for (i=0;i<=13;i++) {
for (j=0;j<=13;j++) {
distancias[i][j] = sqrt(pow(vectorposicion[i][0] - vectorposicion[j][0], 2)
+ pow(vectorposicion[i][1] - vectorposicion[j][1], 2)
+ pow(vectorposicion[i][2] - vectorposicion[j][2], 2));
}
}
CAPÍTULO 6. PROGRAMA
53
} //end distancia
//#############################
Imprime el arreglo ###########################
void imprimir(char vectorarreglo[]){
int i;
for (i=0;i<14;i++) cout <<vectorarreglo[i]<< " ";
}//end arreglo
//################# Escoge de manera aleatoria el orden del arreglo ###########
void escoger(long &idum, char *vector[]) {
int i,
lugar,
bandera,
vectorlugar[14];
float x;
for(i=0;i<=13;i++) {
vectorlugar[i]=1;
}
for(i=0;i<=13;i++) {
bandera = 0;
while(bandera==0) {
x = ran0(idum);
lugar = (int)(14*x);
if(vectorlugar[lugar]==1) {
bandera=1;
}//end if
}//end while
vectorlugar[lugar] = 0;
vectorarreglo[i] = *vector[lugar];
}//end for
}//End escoger
CAPÍTULO 6. PROGRAMA
54
//############### Funcion que calcula la energia cuando los tomos son iguales #
void energia_iguales(double x, double y) {
int i, j;
float ener;
for (i=0; i<=13; i++) {
for(j=0; j<=13; j++) {
if(i!=j) {
energiasub[i][j] = x * (1/ (pow(distancias[i][j], 12))
- y / (pow(distancias[i][j], 6)));
}//end if
}
}
}//end energia_iguales
//########## Funsion que calcula la energia total de la configuracion #########
float energia() {
int i,
j;
float ener;
//Calculo de la energia para atomos iguales
if (tip==1) { //cu-cu
energia_iguales(0.77642641, 0.005503043);
}//end if
if (tip==3) { //Pd-Pd
energia_iguales(4461.183165, 0.004506944488);
}
if (tip==5) {// Pt-Pt
energia_iguales(4122.641609, 0.00871746846);
} //end if
//calculo de energia para atomos diferentes
if (tip==2) { // Cu-Pd
for (i=0;i<=13;i++) {
CAPÍTULO 6. PROGRAMA
55
for (j=0;j<=13;j++) {
if(i!=j) { //A es igual a Cu y B igual a Pd
if ((vectorarreglo[i]==’A’) && (vectorarreglo[j]==’A’)) { //cu-cu
energiasub[i][j] = 0.77642641 * (1/ (pow(distancias[i][j], 12))
- 0.005503043 / (pow(distancias[i][j], 6)));
}//end if
if (((vectorarreglo[i]==’A’) && (vectorarreglo[j]==’B’)) ||
((vectorarreglo[i]==’B’) && (vectorarreglo[j]==’A’))) { //cu-pd
energiasub[i][j]= 1906.34801490418 * (1/ (pow(distancias[i][j], 12))
- 0.0107109126 / (pow(distancias[i][j], 6)));
}//end if
if ((vectorarreglo[i]==’B’) && (vectorarreglo[j]==’B’)) {
energiasub[i][j] = 4461.183165 * (1/ (pow(distancias[i][j],12))
- 0.004506944488 / (pow(distancias[i][j],6)));
}//end if
}//end if
}//end for
}
}//end if
if (tip==4) { // Cu-Pt
for (i=0;i<=13;i++) {
for (j=0;j<=13;j++) {
if(i!=j) { //A es igual a Cu y B igual a Pt
if ((vectorarreglo[i]==’A’) && (vectorarreglo[j]==’A’)) { //cu-cu
energiasub[i][j] = 0.77642641 * (1/ (pow(distancias[i][j], 12))
- 0.005503043 / (pow(distancias[i][j], 6)));
}//end if
if (((vectorarreglo[i]==’A’) && (vectorarreglo[j]==’B’)) ||
((vectorarreglo[i]==’B’) && (vectorarreglo[j]==’A’))) { //cu-pd
energiasub[i][j]= 3488.762665* (1/ (pow(distancias[i][j], 12))
- 0.0110712649 / (pow(distancias[i][j], 6)));
}//end if
if ((vectorarreglo[i]==’B’) && (vectorarreglo[j]==’B’)) {
energiasub[i][j] = 4122.641609 * (1/ (pow(distancias[i][j],12))
- 0.00871746846 / (pow(distancias[i][j],6)));
}//end if
CAPÍTULO 6. PROGRAMA
56
}//end if
}//end for
}
}//end if
ener=0;
for (i=0;i<=13;i++) {
for(j=0;j<=13;j++) {
ener = ( ener + energiasub[i][j] );
}
}
return ener;
}//end energia
//############################ Montecarlo #####################################
void montecarlo(float temp,long &idum){
int aceptar;
float famc;
float K = 3.166829681e-6; /* Boltzman constant [Hartrees,Degrees] */
float x;
static float ultimaen;
if (cuenta > 1){
if (energiatotal <= ultimaen + 0.0001 ) {
aceptar=1;
} else {
famc=exp((1/(K*temp))*(ultimaen-energiatotal));
x =ran0(idum);
if (x < famc){
aceptar=1;
} else {
aceptar=0;
}
}
}else {
aceptar=1;
}
CAPÍTULO 6. PROGRAMA
if (aceptar) {
energiag[cuenta]=energiatotal;
ultimaen = energiatotal;
sumaenergia = sumaenergia + energiatotal;
cuenta++;
}
j++;
} //End Montecarlo
void ultimo (){
imprimir(vectorarreglo);
}
57
CAPÍTULO 6. PROGRAMA
58
Figura 6.1: Parte 1
CAPÍTULO 6. PROGRAMA
59
Figura 6.2: Parte 2
CAPÍTULO 6. PROGRAMA
60
Figura 6.3: Parte 3
CAPÍTULO 6. PROGRAMA
61
Figura 6.4: Parte 4
CAPÍTULO 6. PROGRAMA
62
Figura 6.5: Parte 5
CAPÍTULO 6. PROGRAMA
63
Figura 6.6: Parte 6
CAPÍTULO 6. PROGRAMA
64
Figura 6.7: Parte 7