Alineamiento temporal no lineal

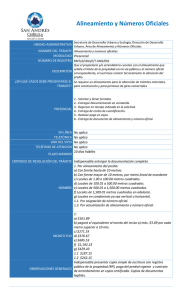
Alineamiento temporal no lineal
Algorı́tmica (Facultad de Informática)
Curso 2006–2007
Podemos definir una métrica entre secuencias de valores que encuentra aplicación en problemas
de reconocimiento de formas. Consideremos un problema de reconocimiento en lı́nea de escritura
manuscrita. El usuario escribe en pantalla letras o dı́gitos de un juego de caracteres preestablecido.
El sistema debe comparar cada trazo del usuario con los que tiene almacenados (de fábrica) y
decidir a cuál se parece más.1 La figura 1 ilustra el problema.
Figura 1: En la lı́nea superior, trazos almacenados en la base de datos “de fábrica” para comparar
con los trazos del usuario. En la lı́nea inferior, un trazo introducido por el usuario y que el sistema
debe clasificar comparándolo con los de la lı́nea superior.
Cada trazo es una secuencia de puntos en el plano y de longitud arbitraria. La figura 2 muestra
un trazo y la secuencia de puntos con que se representa.
67
8
9
1011
1213
14
5
15
16
4
17
18
3
2
19
20
21
1
0
22
23
24
25
26
27
28
29
31
30
32
34
38 42
40
36
33
44
43
35
46
47
45
48
41
3937
49
50
51
52
53
54
55
56
57
58
59
60
61
97
96
95
94
93
92
91
62
63
90
89
88
87
64
65
66
67
68
69
70
86
85
71
83
84
82
8180
73
72
76
75
74
79
7877
Figura 2: Cada trazo es una secuencia de puntos en el plano.
1 Las agendas electrónicas de diseño relativamente reciente suelen integrar software que permite efectuar reconocimiento de escritura manuscrita como el descrito.
1
Pongamos que comparamos dos trazos diferentes del dı́gito 3. Podemos comparar los dos trazos
midiendo la distancia euclı́dea entre pares de puntos ((equivalentes)) en ambas sucesiones de puntos.
El problema surge a la hora de definir ((equivalentes)): las dos secuencias pueden tener diferente
número de puntos y, aun en el caso de que tuvieran idéntica cantidad, un alineamiento punto
a punto no pondrı́a en correspondencia partes similares de cada trazo. Interesarı́a idear algún
método que supiera alinear las partes similares de dos trazos. Si dispusiésemos de un método para
calcular alineamientos serı́a sencillo definir una medida de disimilitud entre trazos: la suma de
distancias entre puntos alineados. La figura 2 ilustra por qué cabe esperar que esta técnica ofrezca
buenos resultados: a mano izquierda se muestra un alineamiento óptimo en cierto sentido entre dos
instancias de un 3 y, a mano derecha, un alineamiento óptimo entre una instancia de un 3 y otra
de un 4. El alineamiento se visualiza gráficamente con lı́neas que unen los puntos emparejados. La
suma de distancias entre pares de puntos alineados es claramente menor al alinear dos instancias
de un mismo dı́gito que al hacer lo mismo con instancias de dı́gitos distintos.
Figura 3: A la izquierda, alineamiento óptimo entre dos trazos que representan a un 3. A la derecha,
alineamiento óptimo entre el trazo de un 4 y el de un 3. Los puntos alineados en cada caso se
muestran unidos por una lı́nea recta. La longitud de dicha lı́nea es, naturalemente, la distancia
euclı́dea entre los puntos. Es evidente que la suma de longitudes entre puntos alineados (ası́ como
la longitud media) es menor al comparar dos instancias de un mismo dı́gito que al comparar
instancias de dı́gitos diferentes.
Si seguimos esta aproximación hemos de definir qué es un alineamiento óptimo. Pues bien, la
definición guarda relación con el propio concepto de disimilitud: el alineamiento óptimo es aquel
que hace mı́nima la suma de distancias entre puntos alineados.
Planteemos formalmente el problema. Dadas dos secuencias a = (a1 , a2 , . . . , am ) y b = (b1 , b2 , . . . , bn ) ∈
(R×R)+ , definimos un alineamiento entre a y b como una secuencia de pares ((i1 , j1 ), (i2 , j2 ), . . . , (ip , jp ))
tal que:
(i1 , j1 ) = (1, 1);
(ip , jp ) = (n, m);
(ik−1 , jk−1 ) 6= (ik , jk ), para 1 < k ≤ p;
ik−1 ≤ ik y jk−1 ≤ jk , para 1 < k ≤ p.
Si no desemos que el alineamiento deje ((huecos)) (pares de puntos sin alinear), hemos de añadir
una restricción adicional
0 ≤ ik − ik−1 ≤ 1 y 0 ≤ jk − jk−1 ≤ 1, para 1 < k ≤ p.
2
Sea2 X(a, b) el conjunto de alineamientos entre a y b. Definimos la distancia de alineamiento
temporal no lineal (DTW, por el inglés ((Dynamic Time Warping))) entre a y b como
X
DTW(a, b) =
mı́n
d(aik , bjk ),
((i1 ,j1 ),(i2 ,j2 ),...,(ip ,jp ))∈X(a,b)
1≤k≤p
donde d(aik , bjk ) es la distancia entre dos puntos (y que nosotros asumiremos que es la distancia
euclı́dea).
Mostramos la ecuación recursiva con DTW(i, j) para hacer referencia a DTW(a1:i , b1:j ):


d(a1 , b1 ),



DTW(1, j − 1) + d(a1 , bj ),


DTW(i − 1, 1) + d(a , b ),
i 1

DTW(i, j) =



 DTW(i − 1, j) + d(ai , bj ),




mı́n
DTW(i, j − 1) + d(ai , bj ),





DTW(i − 1, j − 1) + d(ai , bj )
si i = 1 y j = 1;
si i = 1 y j > 1;
si i > 1 y j = 1;



, si i > 1 y j > 1.


2 Hay definiciones alternativas de alineamiento. En aras de la brevedad y simplicidad de exposición, no entraremos
a considerarlas.
3