metodo de karnaugh
Anuncio

MÉTODO DE KARNAUGH
Jesús Pizarro Peláez
MÉTODO DE KARNAUGH............................................................................................. 1
1.
2.
3.
4.
5.
INTRODUCCIÓN ....................................................................................................... 1
MÉTODO DE KARNAUGH .......................................................................................... 2
EJEMPLO DE APLICACIÓN (I) ..................................................................................... 4
ESTADOS NO IMPORTA EN LAS FUNCIONES LÓGICAS .................................................. 6
EJEMPLO DE APLICACIÓN (II) .................................................................................... 7
1. INTRODUCCIÓN
En ocasiones, el método algebraico para simplificar funciones lógicas aplicando los teoremas del álgebra de
Boole, puede no ser el mejor medio por varias razones:
o
Cuando aumenta el número de variables o de términos resulta difícil ver la forma de reducir la
expresión.
o
Se trabaja con grandes cantidades de expresiones muy similares a ·b·c·d + a ·b·c ·d ... por lo que la
probabilidad de equivocarse en algún paso es muy elevada (y aunque no nos equivoquemos, siempre
resulta farragoso).
o
Podemos llegar a una expresión que no es la óptima, con el consiguiente incremento en puertas y
complejidad del circuito final.
Existe un método gráfico para simplificación de funciones que resuelve todos estos problemas: El método de
Karnaugh. Con este método la simplificación adquiere las siguientes ventajas con respecto al método algebraico:
o
Para funciones de tres y cuatro variables se aplica de forma muy sencilla. Para cinco variables puede
resultar algo más difícil, y para más… existen otros métodos.
o
No se escriben las expresiones de los productos de las variables, se trabaja directamente sobre un
diagrama, por lo que se gana considerablemente en claridad.
o
Con un poco de soltura (adquirida mediante un poco de práctica), resulta muy sencillo hallar siempre
la expresión más óptima de la función.
Es por todos estos motivos que el método de Karnaugh sea ampliamente utilizado para sistemas de tres y cuatro
variables. A todo esto hay que añadir otra gran ventaja: Es un método muy sencillo de aprender, como vamos a ver a
continuación.
1
2. MÉTODO DE KARNAUGH
El método de Karnaugh es un método gráfico. Se usan unas tablas llamadas tablas o diagramas de Karnaugh.
Dichas tablas tienen una casilla por cada combinación de variables de la función, de forma que para 3 variables
tendremos 23 = 8 casillas, para cuatro variables tendremos 24 = 16 casillas.
ba
dc
00
01
11
10
ba
00
c
00
01
0
11
1
01
11
10
10
Diagrama de Karnaugh para 4 variables
Diagrama de Karnaugh para 3 variables
Nótese que el orden de las combinaciones no es binario natural si no que es código Gray (00, 01, 11, 10) esto es
debido a que el funcionamiento del método se basa en combinaciones adyacentes.
Una vez dibujado el diagrama, se trasladan a éste las combinaciones de la tabla de la verdad poniendo un 1 en la
casilla correspondiente. Ejemplo: sea la función
combinaciones
f = a·b·c + a·b·c + a·b·c que como se ve, vale 1 para las
{c, b, a} = {1,0,0}, {0,0,1}, {1,0,1} . Pues en el diagrama de Karnaugh pondríamos un 1 en cada una
de esas casillas.
ba
00
01
10
c
1
0
1
1
1
Casillas donde f = 1
Ahora es cuando vamos a simplificar. A partir de las posiciones de los unos en la tabla, intentamos formar
grupos de unos lo más grandes posibles. Dichos grupos de unos:
-
Deberán estar constituidos por un numero de unos que sea potencia de dos (no valen 3 ni 6 ni 7…).
-
Deberán ser un conjunto convexo (o sea, no tener esquinas hacia dentro).
-
No podrán ir en diagonal.
-
Intentaremos formar el menor número de grupos y éstos deberán ser lo más grandes posible.
-
Un uno puede formar parte de tantos grupos como haga falta.
En los grupos que formemos se eliminan las variables que estén presentes en el cero y en el uno. En nuestro
diagrama anterior, vemos que podemos hacer dos grupos de dos variables: uno con las casillas
2
{c, b, a} = {1,0,0}, {1,0,1}
y otro con
{c, b, a} = {0,0,1}, {1,0,1}
Vemos que en el primer grupo la variable a
aparece con 1 y con 0, por lo que la eliminamos, quedándonos c=1 y b=0 por lo que el término nos queda
b·c . En
el segundo grupo aparece la c negada y sin negar, por lo que la eliminamos, quedándonos b=0 y a=1 por lo que el
término nos queda
b·a . Por lo que la función simplificada queda: f = c·b +·b·a = b·(a + c) .
A continuación se ponen unos cuantos ejemplos de grupos posibles para un diagrama de cuatro variables.
ba
ba
dc
00
01
11
10
dc
ba
00
01
11
10
00
00
dc
ba
00
01
11
10
00
1
1
1
1
1
1
dc
00
01
1
00
1
1
1
01
1
1
01
1
1
01
11
11
1
1
11
11
1
1
10
10
10
10
1
1
1
01
No cambia ninguno, por
lo que
f = d ·c·b·a
ba
ba
dc
Cambian b y d, por lo
que queda f = a·c
00
01
11
10
dc
01
11
00
01
01
1
11
11
1
1
Cambia a, por lo que
queda
f = d ·c·b
00
01
11
10
Cambia d, por lo que
queda f = c·b·a
dc
00
00
01
01
11
11
1
1
10
10
Cambia b, por lo que
queda
f = d ·c·a
dc
f =d
que queda
01
11
1
1
1
10
01
11
10
1
1
1
1
1
Cambian d y b, por lo
que queda
f = c·a
dc
00
1
01
01
1
11
11
1
10
10
1
Cambian a y b, por lo
que queda
dc
f =b
ba
00
f = d ·c
ba
00
10
Cambian a, c y d, por lo
00
00
ba
ba
dc
10
10
1
que queda
ba
00
00
10
Cambian a, b y c, por lo
11
01
11
10
Cambian d y c, por lo
que queda
f = b·a
ba
00
01
1
11
10
1
dc
00
01
11
10
00
1
1
01
01
1
1
11
11
1
1
10
1
1
00
10
1
1
Cambian d y b, por lo
que queda
f = c·a
Cambian b, c y d, por lo
que queda
f =a
Observemos que los cuatro últimos ejemplos no parecen cumplir con lo que dijimos acerca de los grupos, que
debían ser un conjunto convexo. En realidad si que lo son. Debemos ver los diagramas de Karnaugh como una
superficie continua, algo así como una caja de cartón desmontada que cuando se monta se cierra y se unen los lados.
Se pueden coger estos grupos siempre que queramos, sin más condición que ser potencia de 2 y no ir en diagonal.
3
3. EJEMPLO DE APLICACIÓN (I)
Vamos a resolver un problema de lógica combinacional aplicando el método de Karnaugh para obtener la
función simplificada.
Problema
Diseñar un circuito combinacional que realice la división entre 3 (entera) de un número codificado en BCD.
Como ya se sabe, la división entera de un número tiene dos partes: cociente y resto, ambos enteros. Nuestro
circuito hará la división de un número BCD (o sea, del 0 al 9) entre 3. El cociente más grande será el obtenido al
dividir el número más grande, que en BCD es el 9. Como 9:3 = 3 necesitamos 2 bits para representar este número
por lo que nuestro circuito deberá tener dos salidas. Una para el bit de más peso y otra para el de menos peso. A
continuación se muestra la salida del circuito y la tabla de verdad.
Número
resultado
0
0
1
0
2
0
3
1
4
1
5
1
6
2
7
2
8
2
9
3
D C B A b1 b0
División entre 3 de los números del 0 al 9
0
0
0
0
0
0
0
0
1
0
0
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
1
0
1
0
1
0
1
0
0
0
0
0
0
0
1
1
1
0
0
0
1
1
1
0
0
0
1
0
0
1
1
1
Tabla de verdad del circuito
Nos van a quedar dos funciones de 4 variables cada una, lo cual es mucho para poder simplificar por el método
algebraico, por lo que usaremos el método de Karnaugh. Usaremos dos diagramas de Karnaugh; uno para la variable
b1 y otro para b0.
ba
dc
ba
00
01
11
10
dc
00
00
00
01
01
11
11
10
10
b1
01
11
10
b0
4
En primer lugar rellenamos los diagramas con unos en los lugares donde corresponda. b1 en las posiciones
{(0,1,1,0), (0,1,1,1), (1,0,0,0), (1,0,0,1)} y b0 en las posiciones {(0,0,1,1), (0,1,0.0), (0,1,0,1), (1,0,0,1)}
ba
dc
ba
00
01
11
10
00
00
01
1
1
11
01
11
10
1
00
01
10
dc
1
1
11
1
1
1
10
b1
b0
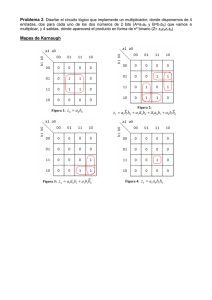
Ahora buscamos grupos de unos lo más grandes posible. Vemos que para b1 tendremos dos grupos de dos unos:
{(0,1,1,1), (0,1,1,0)} y otro por {(1,0,0,0), (1,0,0,1)} . Mientras que para b0 tendremos un grupo
de dos unos formado por {(0,1,0.0 ), (0,1,0,1)} y dos grupos de un solo uno correspondientes a las combinaciones
{(0,0,1,1)} y {(1,0,0,1)}.
uno formado por
ba
dc
ba
00
01
11
10
00
00
01
1
1
11
01
11
10
1
00
01
10
dc
1
1
11
1
1
b1
10
1
b0
A partir de estos diagramas obtenemos directamente las ecuaciones del circuito. Para b1 tendremos dos
términos: en el primer grupo (el de arriba) cambia la a, mientras que dcb = 011 por lo que nos queda
grupo de abajo cambia la a también, por lo que nos queda
d ·c·b . En el
d ·c·b . Para b0 operamos de la misma forma.
Observemos que vamos a tener tres términos, dos de los cuales tendrán todas las variables. Cuanto menores sean los
grupos, menos variables desaparecen y por tanto más variables aparecerán en la expresión final.
Las ecuaciones de nuestro circuito serán:
b1 = d ·c·b + d ·c·b
b0 = d ·c·b·a + d ·c·b·a + d ·c·b
A partir de estas ecuaciones ya podemos implementar nuestro circuito. Nótese que mediante el método de
Karnaugh lo que obtenemos es la expresión mínima de la función expresada en forma de suma de productos. Esto no
quiere decir que la función no se pueda simplificar más. En ocasiones podremos, pero ya no será una expresión en
forma de suma de productos. En este caso, podríamos encontrar una expresión más simple para b0:
b0 = d ·c·b·a + d ·c·b·a + d ·c·b = a·c·(d ·b + d ·b) + d ·c·b = a·c·(b ⊕ d ) + d ·c·b
5
4. ESTADOS NO IMPORTA EN LAS FUNCIONES LÓGICAS
En ocasiones, podemos encontrar combinaciones de entrada para las que no existe definida una salida. No
estamos hablando de que sea 1 o 0, nos referimos a que simplemente, no se va a dar dicha combinación a la entrada,
o si se da, carece de sentido.
Para entender esto mejor pongamos un ejemplo: Sea un tanque de agua con tres sensores (boyas) que indican el
nivel del agua. Si se activa el sensor 1 (combinación 001), significa que el agua llega a ese nivel. Si el agua sube, se
activará también el segundo sensor (combinación 011), y así sucesivamente. De forma que la combinación 000
corresponde al tanque vacío, 111 al tanque lleno, etc.
3
2
1
Pero ¿qué pasa con la combinación 110, por ejemplo? ¿Qué quiere decir esta combinación? Pues lo que quiere
decir, es que el agua ha activado los sensores 2 y 3, pero no el sensor 1. Por lo que sabemos de física esto es
imposible, ya que el agua no flota en el aire, por lo que es imposible que se activen los sensores 2 y 3 si antes no se
ha activado el sensor 1. Esta combinación de entrada nunca se va a dar en nuestro sistema. Hay más combinaciones
que nunca se van a dar como la 100, 101… ¿Qué hacemos con estas combinaciones a la hora de diseñar nuestro
circuito?
Como son combinaciones que no se van a dar, la función para estos valores no estará definida. Esto quiere decir
que la salida para esa combinación de entrada puede ser cualquier cosa, 1 o 0. Nos da igual que tome un valor u otro,
ya que, repetimos: Esa combinación de entrada no se va dar.
A estas combinaciones imposible se las denomina “estados no importa” y se representan en la tabla de verdad
como una x. Al valor x le podemos asignar el valor lógico 0 o 1 según nos convenga uno u otro.
Se representan a continuación la tabla de verdad y los diagramas de Karnaugh de este sistema. La entrada son
los tres sensores y la salida el valor binario del nivel del agua entre 0 y 3 (dos bits). Obsérvese como para las
combinaciones imposibles (010, 100, 101 y 110) se ha puesto a la salida el estado lógico “no importa” representado
por una x. Al trasladar nuestra tabla de la verdad a los diagramas de Karnaugh trasladamos los unos y las x a las
casillas que corresponda.
Ahora hacemos los grupos teniendo en cuenta que podemos usar las x como queramos, o sea, hacer que sean un
1 lógico si con ello conseguimos reducir el número de grupos o hacer los grupos mayores.
6
C
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
A b1 b0
0 0 0
1 0 1
0 X X
1 1 0
0 X X
1 X X
0 X X
1 1 1
Tabla de Verdad
ba
c
ba
00
01
0
1
X
X
11
10
c
1
X
0
1
X
1
00
01
11
10
1
X
b1
X
X
1
X
b0
Diagramas de Karnaugh
No es necesario continuar con el problema para darnos cuenta que hemos conseguido reducir considerablemente
el número de funciones lógicas necesarias. Siempre que podamos, deberemos observar si en nuestro circuito van a
aparecer estados no importa, ya que usarlos supondrá un ahorro considerable de puertas lógicas en la mayoría de los
casos.
5. EJEMPLO DE APLICACIÓN (II)
Para ver la importancia de aplicar los estados no importa al diseño de sistemas digitales, vamos a resolver de
nuevo el problema del apartado 3 aplicando los que hemos aprendido acerca de los no importa.
Problema
Diseñar un circuito combinacional que realice la división entera de un número codificado en BCD entre 3.
Esta era la tabla de verdad que obtuvimos anteriormente:
Número
resultado
0
0
1
0
2
0
3
1
4
1
5
1
6
2
7
2
8
2
9
3
División entre 3 de los números del 0 al 9
D C B A b1 b0
0
0
0
0
0
0
0
0
1
0
0
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
1
0
1
0
1
0
1
0
0
0
0
0
0
0
1
1
1
0
0
0
1
1
1
0
0
0
1
0
0
1
1
1
Tabla de verdad del circuito
7
Si nos fijamos, vemos que la tabla de verdad no está completa. Para 4 bits hay 16 combinaciones de entrada y
nosotros solo hemos puesto 10. ¿Por qué? Porque en BCD no se usan las combinaciones superiores, aquellas
correspondientes a los números decimales 10, 11,… 15.
Pero nosotros, sin darnos cuenta, si que las hemos usado, las hemos asignado el valor 0 como se ve en los
diagramas de Karnaugh:
ba
dc
ba
00
01
11
10
00
00
01
1
1
11
01
11
10
1
00
01
10
dc
1
1
11
1
1
1
10
b1
b0
Deberíamos incluir en nuestros diagramas de Karnaugh dicha combinaciones como x, en lugar de como 0:
ba
dc
ba
00
01
11
10
00
dc
00
01
01
11
10
1
00
1
1
01
1
1
X
X
X
X
1
X
X
11
X
X
X
X
11
10
1
1
X
X
10
b1
b0
Ahora, para realizar los grupos usaremos las x que acabamos de añadir como 1 o como 0 lógico en función de lo
que más nos convenga para conseguir el menor número de grupos, o bien que éstos sean lo más grandes posible:
ba
dc
ba
00
01
11
10
00
dc
00
01
01
11
10
1
00
1
1
01
1
1
X
X
X
X
1
X
X
11
X
X
X
X
11
10
1
1
X
X
10
b1
b0
En esta ocasión nos queda:
b1 = d + c·b
b0 = c·b + d ·a + c·b·a
Que como vemos son expresiones bastante menos complejas que las obtenidas en el apartado 3… y además el
circuito se va a comportar exactamente de la misma manera.
8