Relaciones binarias En esta sección estudiaremos formalmente las

Relaciones binarias
En esta sección estudiaremos formalmente las parejas de objetos que comparten
algunas características o propiedades en común. La estructura matemática para
agrupar estas parejas en conjuntos es la teoría de relaciones binarias.
Las relaciones son de fundamental importancia en el área de computación. Una
estructura compuesta de datos, tal como un arreglo, lista, o árbol, es generalmente
usada para representar simultáneamente a un conjunto de datos y a una relación
que se cumple entre los miembros del conjunto.
Para poder introducir el concepto de relación binaria necesitamos precisar lo que
significa un par ordenado de objetos y definir el producto cartesiano de dos
conjuntos.
El concepto de par ordenado es un ejemplo particular de sucesión con dos
elementos.
Par ordenado. Un par ordenado es un conjunto con dos elementos en un orden
específico. Usamos la notación ( a, b) para denotar el par ordenado en la cuál el
primer elemento o componente es “a” y el segundo elemento objeto es “b”.
De esta forma, dos pares ordenados ( a, b) y (c,d) son iguales si sus
correspondientes componentes son iguales. Es decir,
( a, b) = ( c, d) si y solamente si a = c y b = d
Así mientras que los conjuntos { a, b} y { b, a } son iguales, los pares ordenados
(a, b) y ( b, d) son diferentes.
El concepto de de producto cartesiano se basa en el concepto de pareja
ordenada.
Producto cartesiano. El producto cartesiano de dos conjuntos A y B es el
conjunto de todos los pares ordenados (x, y) donde x∈A e y ∈ B. En símbolos,
A x B = {(x, y) / x∈A ∧ y ∈ B }
Por lo tanto
(x, y) ∈ A x B si y sólo si x∈A ∧ y ∈ B
Ejemplo:
Sean los conjuntos A={1,2,3} y B={4,5,6} se tiene:
A x B={(1,4),(1,5),(1,6),(2,4),(2,5),(2,6),(3,4),(3,5) ,(3,6)}
El producto cartesiano A x B no es igual al producto cartesiano B x A (no es
conmutativo)
Si los conjuntos A y B tienen elementos comunes, entonces los elementos del
producto cartesiano de la forma (a, a), se les llama elementos diagonales.
Si el producto cartesiano fuese de un mismo conjunto A x A puede escribirse de
forma simbólica como A2.
Si el producto cartesiano lo forman más de dos conjuntos, los elementos del
producto cartesiano lo formaran grupos de elementos tomados ordenadamente de
cada uno de los conjuntos que lo forman tomando un elemento del primer
conjunto, otro del segundo otro del tercero y así hasta llegar al ultimo.
Para representar gráficamente el producto cartesiano utilizaremos la
representación cartesiana que consiste en trazar unos ejes perpendiculares, en el
eje horizontal colocaremos los elementos del conjunto A y en el eje vertical los
elementos del conjunto B, los elementos del producto cartesiano los forman los
puntos de intercepción que se obtienen al trazar por los elementos del conjunto A
paralelas al eje vertical y por los elementos del conjunto B paralelas al eje
horizontal.
Para saber el número de elementos del producto cartesiano nos fijaremos en el
diagrama de árbol
tenemos nueve elementos, que es el resultado de multiplicar el número de
elementos del conjunto A por los del conjunto B.
Relaciones entre conjuntos
Llamamos relaciones entre los conjuntos A y B y que representaremos por la letra
R, a cualquier subconjunto del producto cartesiano A x B. (No es necesario que
todos los elementos de A estén considerados)
R : A→ B
Una relación presenta los siguientes elementos
Elemento homólogo o imagen
Se dice que “b” es homólogo o imagen de “a” a todo elemento del conjunto B tal
que el par (a, b) pertenece al subconjunto relación R es decir:
(a, b) ∈ R
Siendo R el subconjunto relación.
La primera componente del par (a, b) que pertenece a G se llama preimagen,
mientras que la segunda componente recibe el nombre de elemento imagen.
Cuando b es el elemento imagen de a por la relación R escribiremos b = R(a)
Conjunto origen, de partida o inicial. Llamaremos así al conjunto A
Conjunto de llegada o final. Es el conjunto B
Se llama conjunto Dominio, y lo designaremos por Dom(R) al conjunto formados
por todos los elementos de A que son preimagen por la relación R (o que tienen
una imagen).
Se llama conjunto recorrido, y se representa por Rec(R) al conjunto formado por
todos los elementos de B que son elementos imágenes por la relaciones R.
Gráfico o Grafo de una Relación:
Es el conjunto de puntos
Graf (R) = { (x, y ) ∈ A x B / y = R(x) ∀x∈A } ⊂ ℜ 2
Relación inversa
Se llama relación inversa a la relación que resulta de cambiar el orden de los
conjuntos A x B por B x A
La relación inversa la designaremos por R −1
Ejemplo:
Sea R la relación definida por:
La relación inversa G-1 será:
G = {(a,1),(a,2),(b,3),(c,5)}
G-1= {(1,a),(2,a),(3,b),(5,c)}
Función:
Se llama función entre los conjuntos A y B a la relación de A en B f : A → B tal
que:
Todos y cada uno de los elementos de A son elementos del dominio y …
la imagen de cada elemento de A es única.
Relaciones binarias
Se llama relación binaria definida en un conjunto A, a la relación de A en A.
Propiedades que pueden cumplir las relaciones binarias son: Reflexiva,
Simétrica,
Antisimétrica
Transitiva
Relación reflexiva cuando un elemento esta relacionado con sigo mismo y se
escribe a R a ∀a∈A.
Ejemplo:
1) En N la relación R definida por: “x R y ⇔ x divide a y”
es reflexiva ya que ∀x∈N, x R x porque x divide a x
2) En N la relación R definida por:
“a R b ⇔ a es el doble de b”.
no es reflexiva ya que (1, 1) ∉R puesto que 1 no es el doble de 1
Si la relación R es reflexiva entonces la diagonal pertenece a
la relación.
Relación Simétrica si para todo par de elemento ocurre que si el elemento a esta
relacionado con el elemento b, entonces el elemento b esta relacionado con el
elemento a.
si ∀ a, b ∈A: a R b ⇒ b R a
Ejemplo:
1) En Z la relación R definida por: “a R b ⇔ a – b es múltiplo de 2”.
es simétrica ya que si a R b ⇒ hay p∈Z tal que a – b = 2p
⇒ b – a = 2(-p) con -p ∈ Z ⇒ b R a
2) En N la relación R definida por: “x R y ⇔ x divide a y”
no es simétrica ya que 2 R 4 porque 2 divide a 4 pero 4 no divide a 2
tanto (4,2) ∉R
Si la relación R es simétrica sobre A entonces los
pares relacionados se reflejan respecto a la diagonal
principal.
por lo
Relación Antisimétrica si para todo par de elemento ocurre que el elemento a
esta relacionado con el elemento b, entonces el elemento b esta relacionado con
el elemento a, y además, se deduce que a = b.
si ∀ a, b ∈A: [a R b ∧ b R a] ⇒ a = b
Otra manera de expresarlo:
Si a≠b ⇒ [ (a,b) ∉ R ∨ (b,a) ∉ R ]
Ejemplo:
1) En N la relación R definida por: “x R y ⇔ x divide a y” es antisimétrica
Ya que si a R b y b R a entonces existen n, m ∈N tales que:
b = an y a = bm. Combinándolas, a = bm = (a.n).m ⇒ n.m = 1 ⇒
n = m = 1 ⇒ a = b.
2) En Z la relación R definida por: “a R b ⇔ a – b es múltiplo de 2”.
no es antisimétrica ya que 2R4 y 4R2, pero 2≠4
Si la relación R es antisimétrica pueden existir pares por
encima o por debajo de la diagonal pero ningún par tiene
reflejo respecto a la diagonal principal excepto la diagonal
misma.
Relación Transitiva cuando se verifica que si el elemento a esta relacionado con
el elemento b y el elemento b esta relacionado con el elemento c; entonces el
elemento a esta relacionado con el elemento c.
si ∀ a, b, c ∈A: [a R b ∧ b R c] ⇒ a R c
Ejemplo:
1) En N la relación R definida por: “x R y ⇔ x divide a y”
es transitiva ya que si a R b y b R c entonces existen n, m ∈N tales que:
b = an y c = bm. Combinándolas, c = bm = (a.n).m= a(n.m) con n.m ∈N ⇒ b R
c.
2) En N la relación R definida por: “a R b ⇔ a es el doble de b”.
no es transitiva ya que (4, 2) ∈ R y (2, 1) ∈ R puesto que 4 es el doble de 2 y 2 es
el doble de 1, sin embargo 4 no es el doble de 1, de donde (4,1)∉ R
Resumen
Propiedad
R
Se satisface sii
No se satisface sii
Reflexiva
∀a∈A a R a
∃ a∈A (a,a)∉R
Simétrica
∀ a, b ∈A:
aRb⇒bRa
∃ a, b ∈A:
(a, b) ∈ R ∧ (b, a) ∉ R
Antisimétrica
∀ a, b ∈A:
[a R b ∧ b R a] ⇒ a = b
∃ a, b ∈A:
(a, b) ∈ R ∧ (b, a) ∈ R ∧ a ≠ b
Transitiva
∀ a, b, c ∈A:
[a R b ∧ b R c] ⇒ a R c
∃ a, b, c ∈A:
(a, b) ∈ R ∧ (b, c) ∈ R ∧ (a, c) ∉ R
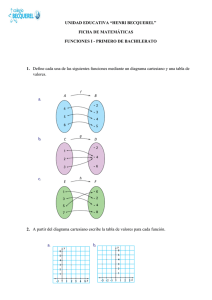
Ejercicios:
1) Sea A = {1, 2, 3, 4}.
i) Represente gráficamente las relaciones (b) y (d) en forma cartesiana y sagital.
ii) Determine las propiedades que satisfacen las siguientes relaciones en A y
verifíquelas (demuéstrelas)
a)
b)
c)
d)
e)
R = { (1,1) , (2,2) , (3,3)}.
R = { (1,1) , (2,2) , (3,3), (4,4) , (1,2) , (1,4) , (2,1), (3,2) , (4,3) }.
R = { (1,1) , (2,2) , (3,3), (4,4)}.
R = { (1,1) , (2,2) , (3,3), (1,2), (3,2) , (2,3) }.
R = { (1,1) , (1,2) , (1,4) , (2,3), (4,3) }.
2) Sea A = {1, 2, 3, 4}. Construya tres relaciones binarias en A con las siguientes
propiedades:
i) Reflexiva, simétrica y no transitiva
ii) Reflexiva, no simétrica y transitiva
iii) No reflexiva, simétrica y transitiva
3) Definimos en ℜ, el conjunto de los números reales, la relación R :
xRy ⇔ x–y∈Ζ
Determine las propiedades que cumple R y demuestre, usando la definición, que
efectivamente las verifica!
Relación de equivalencia
Diremos que una relación binaria sobre A, es una relación de equivalencia si
satisface las tres propiedades:
‰ R es reflexiva
‰ R es simétrica
‰ R es transitiva
Ejemplos
1) En Z la relación R definida por: a R b ⇔ a – b es múltiplo de 3.
2) Dado un conjunto D⊆ U, la relación:
A R B ⇔ A ∩ D = B ∩D
Demuestra que estas son relaciones de equivalencia
Relación de orden
Diremos que una relación binaria sobre A, es una relación de orden parcial si
satisface las tres propiedades:
‰ R es reflexiva
‰ R es antisimétrica
‰ R es transitiva
En este caso diremos que el conjunto A está parcialmente ordenado
Ejemplo:
1) En D60 , el conjunto de todos los divisores de 60, la relación R definida por:
a R b ⇔ a divide a b.
2) En R, la relación definida por a R b ⇔ a ≤ b.
Demuestra que estas son relaciones de orden.
Diremos que una relación binaria R sobre A, es una relación de orden total si es
una relación de orden parcial y además se satisface que:
∀ a, b ∈A: [a R b ∨ b R a]
En este caso diremos que el conjunto A está totalmente ordenado
Ejemplo:
1) En las relaciones anteriores decida cuáles son de orden parcial o de orden
total
2) Para pensar: Considere la relación en R2, definida por:
(x,y) R (a,b) ⇔ x ≤ a ∧ y ≤ b .
¿Qué tipo de relación es?
Leyes de composición
Se dice que en A se ha definido una ley de composición interna u operación
cuando se define una Función del producto cartesiano A x A en A de tal forma que
el par de elementos (a, b) genere otro elemento c, tal que c también pertenece al
conjunto A.
Para representar el elemento imagen del par (a, b) se utiliza la notación c = a f b
donde f es cualquier símbolo. Por ejemplo ⋅ , ⊥ , ∗ , Θ , ° , ◊ , ∇
Se dice que en A se a definido una ley de composición externa sobre el conjunto B
cuando se define una Función del producto cartesiano BXA en A
Propiedades
Asociativa
Se dice que la ley de composición * es asociativa cuando para cualquier
elementos a,b,c pertenecientes al conjunto A se verifica:
(a * b) * c = a * (b * c)
Conmutativa
Se dice que la ley de composición * es conmutativa cuando para cualquier
elementos a,b,c pertenecientes al conjunto A se verifica:
a*b=a*b
Elemento neutro
Se dice que la ley de composición * posee elemento neutro cuando existe un
elemento e de A tal que cualquiera que sea a perteneciente al conjunto A se
verifica:
a*e=a
Elemento Inverso
Se dice que la ley de composición, que posee elemento neutro, es simetrizable
cuando para cualquier elemento de a perteneciente al conjunto A existe un
elemento Inverso a −1 de A tal que:
a*a −1= e
Donde e es el elemento neutro
Distributiva entre dos operaciones
Se dice que la ley de composición * es distributiva respecto de la operación ¤
cuando cualquiera que sean los elementos a, b, c pertenecientes al conjunto A se
verifica:
a * (b ¤ c)= ( a * b ) ¤ ( a * c )
Estructuras algebraicas
Se llama estructura algebraica a todo conjunto en la que se han definido una o
varias leyes de composición
Estructuras algebraicas con una ley de composición
Semigrupo
Se dice que el conjunto A con la ley de composición interna * tiene estructura de
semigrupo si la ley es asociativa.
Si la operación * posee la propiedad conmutativa o elemento neutro o ambas a la
vez, el semigrupo se llama conmutativo, con elemento neutro o conmutativo con
elemento neutro, respectivamente.
Grupo
Se dice que el conjunto A con la ley de composición interna * tiene estructura de
grupo si la ley es asociativa, posee elemento neutro y es simetrizable.
Si la operación * posee la propiedad conmutativa, entonces el grupo se llama
conmutativo o abeliano.
Estructuras algebraicas con dos leyes de composición
Semianillo
Se llama semianillo cuando en el conjunto A hemos definido dos leyes de
composición interna que tienen estructura de semigrupo y además una ley de
composición es distributiva respecto a la otra.
Anillo
Se llama anillo cuando en el conjunto A hemos definido dos leyes de composición
interna una que tiene estructura de grupo y la otra de semigrupo y además una ley
de composición es distributiva respecto a la otra.
Cuerpo
Se llama cuerpo cuando en el conjunto A hemos definido dos leyes de
composición interna que tienen estructura de grupo y además una ley de
composición es distributiva respecto a la otra.
Espacio vectorial
Se llama espacio vectorial a la estructura en la que se ha definido sobre el
conjunto A una estructura de cuerpo conmutativo y una ley externa sobre el
conjunto B que satisfacen las siguientes condiciones:
A con la ley * es un grupo conmutativo
Distributiva de la ley externa ¤ respecto de la interna * en A
Distributiva de la ley externa ¤ respecto de la enterna * en B