Secciones 16: Octaedro por Plano oblicuo BT 2.36
Anuncio
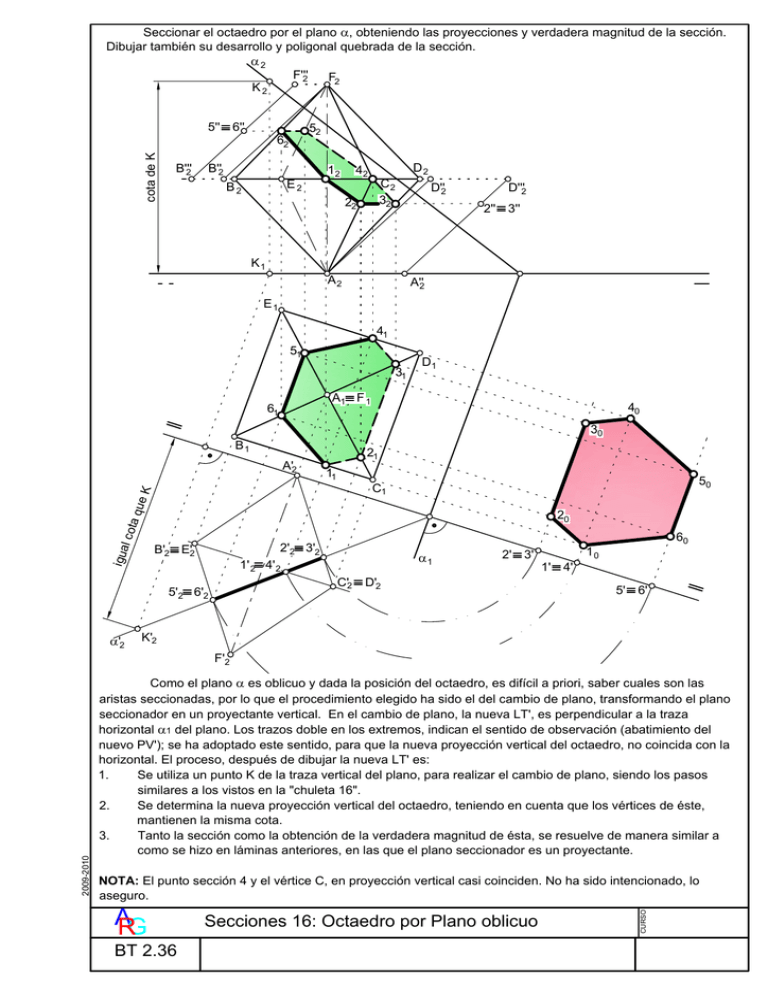
Seccionar el octaedro por el plano α, obteniendo las proyecciones y verdadera magnitud de la sección. Dibujar también su desarrollo y poligonal quebrada de la sección. α2 F'''2 K2 cota de K 5''L 6'' B'''2 52 62 B''2 F2 E2 B2 12 42 C2 32 22 K1 A2 D2 D''2 D'''2 2''L 3'' A''2 E1 41 51 31 D1 A1L F 1 61 40 30 B1 ue K A'2 21 11 50 C1 l co ta q 20 2'2L 3'2 igua B'2L E'2 1'L 4' 5'L 6' K'2 F'2 Como el plano α es oblicuo y dada la posición del octaedro, es difícil a priori, saber cuales son las aristas seccionadas, por lo que el procedimiento elegido ha sido el del cambio de plano, transformando el plano seccionador en un proyectante vertical. En el cambio de plano, la nueva LT', es perpendicular a la traza horizontal α1 del plano. Los trazos doble en los extremos, indican el sentido de observación (abatimiento del nuevo PV'); se ha adoptado este sentido, para que la nueva proyección vertical del octaedro, no coincida con la horizontal. El proceso, después de dibujar la nueva LT' es: 1. Se utiliza un punto K de la traza vertical del plano, para realizar el cambio de plano, siendo los pasos similares a los vistos en la "chuleta 16". 2. Se determina la nueva proyección vertical del octaedro, teniendo en cuenta que los vértices de éste, mantienen la misma cota. 3. Tanto la sección como la obtención de la verdadera magnitud de ésta, se resuelve de manera similar a como se hizo en láminas anteriores, en las que el plano seccionador es un proyectante. NOTA: El punto sección 4 y el vértice C, en proyección vertical casi coinciden. No ha sido intencionado, lo aseguro. A RG BT 2.36 Secciones 16: Octaedro por Plano oblicuo CURSO 2009-2010 2'L 3' C'2L D'2 5'2L 6'2 α'2 α1 1' 2L 4' 2 60 10 C 1 B B B 6 6 A F 1 1 5 2 C 4 4 E 1:1 D C 1 B B B 6 6 A F 1 1 5 C 2 C E 3 4 4 D D E 1:2 C 1 B B 6 A F 1 5 E 2 C C 3 4 4 D D 5 6 F 1 C C 2 A 1 3 4 D E 2 5 6 3 F 1 4 D 5 6 C C D Dado que el octaedro es el resultado de unir por sus bases, dos pirámides, de caras laterales triángulos equiláteros y de base cuadrada; el desarrollo se ha realizado por el de estas dos pirámides, sin el cuadrado base, unidas por una de las aristas, la BE por ejemplo, del cuadrado común. Al igual que se ha visto en casos anteriores, hay que determinar la verdadera magnitud de las aristas, para poder llevar los puntos sección. • Los puntos 1 y 4, los tomamos directamente de sus aristas, en la proyección horizontal, pues esta en verdadera magnitud las aristas a las que pertenecen. • Para los otros, hay que determinar la verdadera magnitud de sus aristas, operación realizada en la proyección vertical, de igual manera a como se hizo en la láminas anteriores, como por ejemplo la del cubo anterior. Una vez llevados los puntos sección, se procede a reordenar las caras, de manera conveniente, como se muestra a la izquierda, para lograr así dos recortables: • La FCB gira 120º respecto del vértice F, hasta juntarse a la EFB por su arista BF. • Hecho lo anterior, el conjunto de las cuatro caras, inscritsa dentro de la poligonal DCFCBE, giran respecto del vértice E, un ángulo de -180º, obteniendo así el desarrollo deseado en dos partes, perfectamente diferenciadas para realizar el recortable. Si separamos por la linea quebrada de la transformada, y pegamos la sección en verdadera magnitud, se tienen los dos desarollos para realizar la construcción en cartulina de los dos cuerpos que quedan después de secionarlos. 2009-2010 1 E 1:4 A RG BT 2.36 Secciones 16: Octaedro por Plano oblicuo CURSO C B B 1 C E 3 Seccionar el octaedro por el plano α, obteniendo las proyecciones y verdadera magnitud de la sección. Dibujar también su desarrollo y poligonal quebrada de la sección. α2 F'''2 K2 cota de K 5''L 6'' B'''2 52 62 B''2 F2 E2 B2 12 42 C2 32 22 K1 A2 D2 D''2 D'''2 2''L 3'' A''2 E1 41 51 31 D1 A1L F 1 61 40 30 B1 ue K A'2 21 11 50 C1 l co ta q 20 2'2L 3'2 igua B'2L E'2 1'L 4' 5'L 6' K'2 F'2 Como el plano α es oblicuo y dada la posición del octaedro, es difícil a priori, saber cuales son las aristas seccionadas, por lo que el procedimiento elegido ha sido el del cambio de plano, transformando el plano seccionador en un proyectante vertical. En el cambio de plano, la nueva LT', es perpendicular a la traza horizontal α1 del plano. Los trazos doble en los extremos, indican el sentido de observación (abatimiento del nuevo PV'); se ha adoptado este sentido, para que la nueva proyección vertical del octaedro, no coincida con la horizontal. El proceso, después de dibujar la nueva LT' es: 1. Se utiliza un punto K de la traza vertical del plano, para realizar el cambio de plano, siendo los pasos similares a los vistos en la "chuleta 16" y en la lámina 2.12. 2. Se determina la nueva proyección vertical del octaedro, teniendo en cuenta que los vértices de éste, mantienen la misma cota. 3. Tanto la sección como la obtención de la verdadera magnitud de ésta, se resuelve de manera similar a como se hizo en láminas anteriores, en las que el plano seccionador es un proyectante. NOTA: El punto sección 4 y el vértice C, en proyección vertical casi coinciden. No ha sido intencionado, lo aseguro. Sólo por curiosidad, el "casi" ha sido de aproximadamente 0,04 mm. A RG BT 2.36 Secciones 16: Octaedro por Plano oblicuo CURSO 2009-2010 2'L 3' C'2L D'2 5'2L 6'2 α'2 α1 1' 2L 4' 2 60 10 C 1 B B B 6 6 A F 1 1 5 2 C 4 4 E 1:1 D C 1 B B B 6 6 A F 1 1 5 C 2 C E 3 4 4 D D E 1:2 C 1 B B 6 A F 1 5 E 2 C C 3 4 4 D D 5 6 F 1 C C 2 A 1 3 4 D E 2 5 6 3 F 1 4 D 5 6 C C D Dado que el octaedro es el resultado de unir por sus bases, dos pirámides, de caras laterales triángulos equiláteros y de base cuadrada; el desarrollo se ha realizado por el de estas dos pirámides, sin el cuadrado base, unidas por una de las aristas, la BE por ejemplo, del cuadrado común. Al igual que se ha visto en casos anteriores, hay que determinar la verdadera magnitud de las aristas, para poder llevar los puntos sección. • Los puntos 1 y 4, los tomamos directamente de sus aristas, en la proyección horizontal, pues esta en verdadera magnitud las aristas a las que pertenecen. • Para los otros, hay que determinar la verdadera magnitud de sus aristas, operación realizada en la proyección vertical, de igual manera a como se hizo en la láminas anteriores, como por ejemplo la del cubo anterior. Una vez llevados los puntos sección, se procede a reordenar las caras, de manera conveniente, como se muestra a la izquierda, para lograr así dos recortables: • La FCB gira 120º respecto del vértice F, hasta juntarse a la EFB por su arista BF. • Hecho lo anterior, el conjunto de las cuatro caras, inscritsa dentro de la poligonal DCFCBE, giran respecto del vértice E, un ángulo de -180º, obteniendo así el desarrollo deseado en dos partes, perfectamente diferenciadas para realizar el recortable. Si separamos por la linea quebrada de la transformada, y pegamos la sección en verdadera magnitud, se tienen los dos desarollos para realizar la construcción en cartulina de los dos cuerpos que quedan después de secionarlos. 2009-2010 1 E 1:4 A RG BT 2.36 Secciones 16: Octaedro por Plano oblicuo CURSO C B B 1 C E 3