6.- Polarización de la onda Electromagnética
Anuncio
Práctica 6
1
______________________________________________________________________________________
Instituto Politécnico Nacional
ESCUELA SUPERIOR DE INGENÍERIA MECÁNICA Y ELÉCTRICA
U. C.
DEPARTAMENTO EN COMUNICACIONES Y ELECTRÓNICA.
ACADEMIA DE ELECTROMAGNETISMO
Práctica N° 6
" Polarización de la onda Electromagnética”
II.- OBJETIVO :
El alumno identificará la polarización de la onda electromagnética de la señal
recibida y aprenderá las técnicas para polarizar las antenas.
III.- BASE TEORICA:
De acuerdo a la definición estándar de la IEEE para antenas, la polarización
de una onda radiada se define como aquella propiedad de una onda electromagnética que
describe en la dirección variante con el tiempo y la magnitud relativa del vector campo
eléctrico; específicamente, la figura trazada como una función del tiempo por la
extremidad del vector en una localización fija en el espacio y el sentido en el cual se traza,
cuando se observa a lo largo de la dirección de propagación.
En otras palabras, la polarización es la curva trazada externamente por la punta de una
flecha la cual representa el campo eléctrico instantáneo. El campo se puede observar a lo
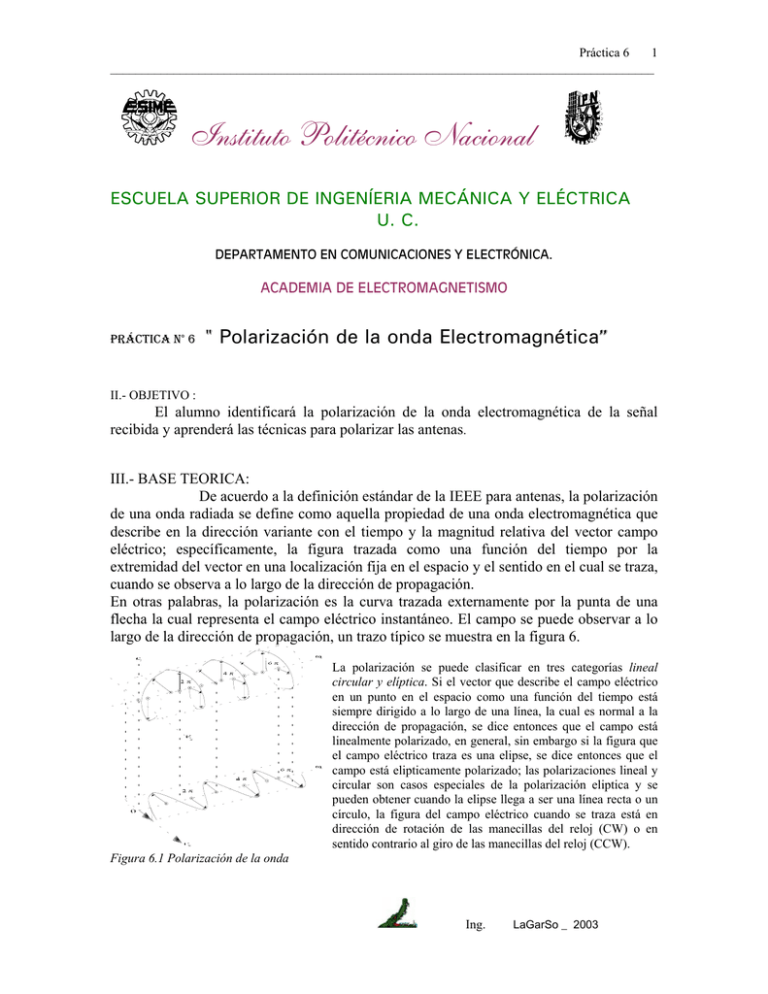
largo de la dirección de propagación, un trazo típico se muestra en la figura 6.
t
y
x
t
x
La polarización se puede clasificar en tres categorías lineal
circular y elíptica. Si el vector que describe el campo eléctrico
en un punto en el espacio como una función del tiempo está
siempre dirigido a lo largo de una línea, la cual es normal a la
dirección de propagación, se dice entonces que el campo está
linealmente polarizado, en general, sin embargo si la figura que
el campo eléctrico traza es una elipse, se dice entonces que el
campo está elipticamente polarizado; las polarizaciones lineal y
circular son casos especiales de la polarización eliptica y se
pueden obtener cuando la elipse llega a ser una línea recta o un
círculo, la figura del campo eléctrico cuando se traza está en
dirección de rotación de las manecillas del reloj (CW) o en
sentido contrario al giro de las manecillas del reloj (CCW).
Figura 6.1 Polarización de la onda
Ing.
LaGarSo _ 2003
2 Laboratorio de Electromagnétismo I
______________________________________________________________________________________
Cuando el giro es en sentido de giro de las manecillas del reloj se dice que la
polarización es a derechas mientras que si el vector gira en sentido contrario al giro en las
manecillas del reloj se dice entonces que la polarización es a izquierdas.
En la figura 6.2 se muestran los esquemas representativos de las polarizaciones, lineal y
circular, a izquierdas y a derechas.
Ex
z
z
Ey
Polarización lineal
Polarización circular
Figura 6.2 polarización lineal y circular.
POLARIZACION LINEAL
Consideremos una onda armonica plana, con las componentes de campo eléctrico viajando
en la dirección z positiva ( hacia la página ) tal y como se muestra en la figura 20, los
campos eléctricos y magnéticos instántaneos están dados como:
)
)
)
)
E = a x Ex + a y Ey = Re [ a x E +x e j ( ω t − β z ) + a y E y e j ( ω t − β z ) ]
)
)
= a x E +xo cos ( ωt −βz +φ x ) + a y E +yo cos ωt −βz +φ y
(
)
)
H = a y Hy + a x Hx
6.1
+
) E+
) Ey j( ω t −β z )
e
= Re [ a y x e j ( ω t − β z ) − a x
]
η
η
+
+
) E
) E yo
= a y xo cos ( ωt −βz +φ x ) − a x
cos ωt −βz +φ y
η
η
(
donde E +x , E +y
)
)
6.2
son complejas y E +xo , E +yo son reales.
Examinemos ahora la variación del campo eléctrico instantáneo del vector eléctrico E tal
y como se dió en la ecuación anterior en el plano
z = 0 .Se pueden considerar otros planos, pero el plano z = 0 se escoje por simplicidad y
conveniencia. Como ejemplo supongamos
Ing.
LaGarSo _ 2003
Práctica 6
3
______________________________________________________________________________________
+
E yo = 0
……
6.3
entonces:
Ex = E +x 0 cos (ωt +φ x ) …… 6.4
Ey = 0
El locus del campo eléctrico instantáneo está
dado por
)
E = a x E +x 0 cos(ωt +φ x ) …… 6.5
La cual es una línea recta y siempre estará
dirigida a lo largo del eje x en cualquier
momento tal y como se muestra en la figura 6.3
se dice entonces que el campo está linealmente
polarizado en la dirección x.
Exo cos(ωt + φx )
z
Ey
Ejemplo: Determine la polarización de la onda
+
dada para la onda cuya expresión para E xo = 0
Solución:
+
puesto que E x0 = 0 entonces Ex = 0;
(
Ey = E 2y 0 cos ωt +φ y
)
6.6
Figura 6.3 campo linealmente polarizado en la direccion x
Ex
El locus del vector campo electrico instántaneo
está dado como :
(
E = â y E +y 0 cos ωt +φ y
)
6.7
La representación es una línea recta la cual está
siempre dirigida a lo largo del eje y siempre, tal y
como se muestra en la figura 6.4, en este caso se
dice que el campo está linealmente polarizado en
la dirección y.
Eyo cos (ωt + φy )
Ey
Figura 6.4 Campo linealmente polarizado en la direccion y
POLARIZACION CIRCULAR
Se dice que una onda está circularmente polarizada si la punta del vector eléctrico
traza un locus circular cuando se desplaza la onda; si el sentido de giro es en dirección de
la rotación de las manecillas del reloj cuando se ve a lo largo del eje de propagación se
dice que la polarización es a derechas.
Como ejemplo examinemos el caso en el cual la propagación se desarrolla
unicamente en el plano xy
El locus para el vector campo eléctrico E en el plano z = 0 siempre es:
Ing.
LaGarSo _ 2003
4 Laboratorio de Electromagnétismo I
______________________________________________________________________________________
φx = 0
ω
φy = - π/2
+
ω
+
E x0 = E y0 = E R
……. 6.8
ω
ω
π
π
π
ω
π
entonces :
ω
Ex = ER cos (ω t )
π
ω
ω
Ey = ER cos (ω t - π/2 ) = ER sen (ω t )
π
π
…. 6.9
El locus de la amplitud del vector campo eléctrico está dado por :
E =
(
)
E 2x +E 2y = E 2R cos 2 ωt + sen 2 ωt = E R
……….. 6.10
y está dirigida a lo largo de una línea que hace un ángulo ψ con el eje x, el cual está dado como
Ey
E senωt
−1
= tan −1 R
……….. 6.11
ψ = tan-1
E cosωt = tan (tanωt )= ωt
E
x
R
Si graficamos el locus del campo eléctrico para varios tiempos en el plano z = 0 se generan las formas de un
círculo de radio ER y gira en sentido de rotación del giro de las manecillas del reloj con una frecuencia
angular ω tal y como se muestra en la figura 6.5. Se dice que la onda está polarizada a derechas. Es
importante señalar que la polarización se observa desde la parte posterior del sentido de propagación de la
onda , en este caso la observación es hacia adentro de la página y perpendicular a ella.
La expresión para el vector para el campo eléctrico instántaneo es de la forma :
[
]
{[
]
E = Re â x E R e j(ωt −βz ) +â y E R e j(ωt −βz −π/ 2 ) = E R Re â x − jâ y e j(ωt −βz )
}
……….. 6.12
POLARIZACION CIRCULAR A IZQUIERDAS
Si el vector campo eléctrico tiene un sentido de rotación en contra del giro de las manecillas del
reloj se dice que la polarización es a izquierdas .
Un ejemplo de este tipo de polarización se muestra a continuación :
Ing.
LaGarSo _ 2003
Práctica 6
5
______________________________________________________________________________________
Sea:
φx = 0
ω
φy = π/2
+
ω
+
E x0 = E y0 = E L
entonces:
Ex = EL cos (ω t )
…….. 6.13
……… 6.14
π
ω
π
ω
π
ω
ω
ω
Ey = EL cos (ω t + π/2 ) = - EL sen ( ω t ) . 6.15
y el locus de la amplitud es
E=
(
ω
π
π
π
π
)
E 2x +E 2y = E 2L cos 2 ωt +sen 2 ωt = E L .. 6.16
el ángulo ψ está dado por :
Ey
−1 −E L senωt
ψ = tan-1 E =tan E cosωt = −ωt
L
x
……. 6.17
El locus del vector de campo eléctrico es un círculo de radio EL y gira en sentido contrario de las manecillas
del reloj, con una frecuencia angular ω tal y como se muestra en la figura 6.6.
El vector del campo eléctrico instántaneo está dado como :
[
] {[
]
E = Re â x E L e j(ωt −βz ) +â y E L e j(ωt −βz+π/ 2 ) = Re â x + jâ y e j(ωt −βz )
}
…….. 6.18
En la expresión anterior se puede notar que existe un avance en la fase de 90º de la componente de Ey
relativa a la componente en Ex .
En general las condiciones necesarias y suficientes para que exista la polarización circular son:
1.- Las componentes de campo deberán tener dos componentes ortogonales linealmente polarizadas.
2.- Las dos componentes deberán tener la misma magnitud.
3.- Las dos componentes deberán tener una diferencia de fase de múltiplos impares de 90º
El sentido de rotación estará siempre determinado por la rotación de la componente adelantada en fase
a la componente retrasada en fase y observando la rotación del campo cuando la onda viaja alejandose del
observador. La rotación de la componente adelantada en fase hacia la componente retrasada en fase
deberá hacerse a lo largo de una separación angular entre las dos componentes la cual es menor de 180º
Fases iguales o mayores de 0º y menores que 180º pueden considerarse de adelanto, mientras que aquellas
iguales o mayores de 180º y menores que 360º se podrán considerar de atraso.
POLARIZACION ELIPTICA
Se dice que una onda está elípticamente polarizada si la punta que el vector eléctrico traza es un locus elipse
en el espacio. La polarización como en el caso de la polarización círcular se clasifica a derechas y a
izquierdas, se dice que la onda está elipticamente polarizada a derechas si el vector campo eléctrico gira en
sentido de rotación del giro de las manecillas del reloj y es a izquierdas si el sentido de rotación del vector
es en contra del giro de rotación de las manecillas del reloj.
Ing.
LaGarSo _ 2003
6 Laboratorio de Electromagnétismo I
______________________________________________________________________________________
Para que se presente la polarización elíptica el vector campo eléctrico E deberá escribirse por medio de una
expresión de la forma:
φx = π/2
ω
π
φy = 0
E +x0 = (ER + EL
E +y0 = (ER − EL
)
ω
)
………… 6.19
ω
π
entonces :
Ex = (ER + EL ) cos ( ω t + π/2 ) = - (ER + EL ) sen ω t
ω
π
Ey = (ER - EL ) cos ( ω t ) ………… 6.20
podemos escribir el locus para el vector campo eléctrico de
la forma
E2 = E 2x +E 2y = (E R +E L )2 sen 2 ωt + (E R −E L )2 cos 2 ωt
….. 6.21
= E 2R sen 2 ωt +E 2L sen 2 ωt + 2E R E L sen 2 ωt + E 2R cos 2 ωt + E 2L cos 2 ωt −2E R E L cos 2 ωt
[
E 2x + E 2y = E 2R +E 2L +2E R E L sen 2 ωt −cos 2 ωt
]
…... 6.22
sin embargo
sen ω t = −
cos ω t =
Ex
ER + EL
Ey
…… 6.23
ER − EL
substituyendo la expresión general se reduce a :
E
x
E R + E L
2
E
y
+
E R − E L
2
=1
……. 6.24
la cual es la ecuación para una elípse con el eje mayor interceptado | E | max = | ER + EL | y la intercepción
del eje menor |E|min = | ER - EL | . Conforme transcurre el tiempo el vector campo eléctrico gira y su
longitud varía y traza una elípse de acuerdo a la figura 6.7
Las longitudes máxima y mínima del vector eléctrico son los ejes mayor y menor interceptados por
|E|max = |ER + EL | cuando ω t = ( 2n + 1 ) π/2 , n = 0,1,2...
|E|min = |ER - EL | cuando ω t = n π , n = 0,1,2,.....
……. 6.25
La razón axial (AR) se define como la razón del eje mayor (incluyendo su signo ) de la elipse de
polarización al eje menor , o
E
E + EL
…… 6.26
AR = − max = − R
Emin
ER − EL
Ing.
LaGarSo _ 2003
Práctica 6
7
______________________________________________________________________________________
donde ER y EL son cantidades reales positivas. Tal y como se definen en la expresión anterior la razón axial
AR se puede tomar como positiva (para polarización a izquierdas ) o negativa (para polarización a derechas)
los valores están en el rango de 1≤|AR|≤∞ .El vector campo eléctrico instántaneo se puede escribr como :
{
E = Re â x [E R +E L ]e j(ωt −βz +π/ 2 ) +â y [E R −E L ]e j(ωt −βz )
[
]
}
j ω t −β z )
E= Re a$ x j (ER + EL ) + a$ y (ER − EL ) e (
{[ (
)
(
)]
E = Re E R jâ x +â y +E L jâ x −â y e j(ωt −βz )
}
……………. 6.27
Estas expresiones nos permiten representar las amplitudes de una onda circularmente polarizada ,el primer
término representa una polarización a derechas, mientras que el segundo término representa una
polarización a izquierdas, dependiendo de la magnitud de las componentes la polarización elíptica estará
orientada a izquierdas o a derechas.
En general para una polarización de este tipo la expresión para la razón axial está dada como :
AR = ±
eje mayor
0A
= ±
eje menor
0B
1 ≤ AR ≤ ∞
……………. 6.28
donde :
2
2
4
4
1
0A = E +x 0 + E +y 0 + E +x 0 + E +y 0 + 2 E +x 0
2
1
2
2
cos(2∆φ )
1
2
( ) ( ) ( ) ( ) ( ) (E )
2
2
4
4
1
0B = E +x 0 + E +y 0 − E +x 0 + E +y 0 +2 E +x 0
2
2
+
y0
…………… 6.29
1
2
2
cos(2∆φ)
1
2
( ) ( ) ( ) ( ) ( ) (E )
2
+
y0
………….. 6.30
donde las expresiones para E +x0 y E +y0 son de la forma:
E +x0 = ER + EL
ω
E +y0 = ER - EL
∆φ = φx - φy ≠ nπ/2
≥0
…….. 6.31
n = 0,1,2,3,.....
ω
ω
π
para CW si ER > EL
para CCW si ER < EL
≤0
π
……. 6.32
ω
para CW si ER < EL
para CCW si ER > EL
…….. 6.33
π
Figura 6.8 Onda electromagnetica elipticamente polarizada
Este tipo de mediciones se pueden obtener con la asistencia de la esfera de Poincaré, los datos relativos a esta técnica se
pueden consultar en el libro de Kraus de Antennas o en el libro de Balanis de Antenas.
IV.- Lista de material :
Ing.
LaGarSo _ 2003
8 Laboratorio de Electromagnétismo I
______________________________________________________________________________________
1.- Generador de luz lasér con interlock
2.-2 transparencias de Polaroid
3.- 2 soportes para transparencias
4.- Una pantalla de visión
5.- 1 generador de microondas
6.- 1 atenuador de compuerta
7.- 2 antenas tipo trompeta
8.- 1 microamperímetro
9.- 1 detector
10.- 1 rejilla de polarización
11.- rejilla de polarización elaborada por los alumnos ( se requiere 1 por equipo a la frecuencia de microondas y una
por grupo a la frecuencia de 167 MHz )
12.- Antena elaborada por el alumno.
V.- Desarrollo y mediciones
Nota Los experímentos que se citan serán desarrollados primeramente por el profesor ante el grupo,
con la finalidad de presentar las técnicas de medición.
1.- Una de las formas de identificar la polarización de las ondas eléctromagnéticas es por medio de polarizadores, a
frecuencias ópticas se pasa el rayo a través del primer polarizador, al salir la onda está polarizada y se pasa a través del
segundo polarizador
Monte el siguiente diagrama:
ly
ro
d
Polyrod
Po
µ
µ
µ
Ω
Figura 6.9 Generador de luz lasér ,transparencias polirod, para la determinación de la polarización de la onda
electromagnética.
2.- Ponga la primera transparencia de polirod con el rótulo hacia arriba y la segunda montela en el
transportador .
3.- Gire el transportador cada 5º y haga una gráfica de intensidad contra posición.
Ponga a la primera transparencia con el rótulo de polirod vertical y repita el experimento.
Nota El laboratorio únicamente dispone de dos transparencias de polirod por lo que esta parte del
experímento el profesor realizará una demostración y durante el transcurso de la semana el experímento lo
pueden realizar en grupos de 6 alumnos, después de clases (13 Hs). Si el alumno tiene lentes polarizados
puede experímentar y considerar la sustitución de las lentes polarizadas
Nota bajo ninguna circunstancia la luz lasér deberá incidir directamente en los ojos sea cuidadoso!!
¿ Que tipo de polarización tiene el generador de luz lasér ?
Ing.
LaGarSo _ 2003
Práctica 6
9
______________________________________________________________________________________
4.- Otra forma que
permite determinar la
polarización de las ondas
electromagnéticas y de ahí
la polarización de la antena
es con la asistencia de una
rejilla de polarización, en
este método se coloca
frente a la antena receptora
la rejilla de polarización y
se gira hasta que se
interrumpe la señal
recibida.
En este momento se
identifica la polarización
de la onda recibida y de
ahí la polarización de la
antena.
Figura 6.11 Sistema de trasmisión a frecuencias de microondas y rejilla de
polarización . Gire la rejilla hasta que la señal se elimine.
Nota.- como terminación puede usar el detector intercostruido en la guía de onda y como terminación
el transformador de guía de onda y cable coaxial y un microamperímetro de 100 µA
5.- Ponga una separación entre antenas del orden de 50 cm y a 10 cm del receptor frente a la antena
receptora coloque la rejilla de polarización dobre su base y registre el valor de la señal.
6.-Gire la rejilla de polarización y mida el nivel de señal en el medidor del generador de microondas
Como se identifica la plarización de la onda ?
7.-Sustituya al medidor en el generador de microondas por un microamperímetro y aumente la separación
entre antenas a 70 cm y repita el experimento
Ing.
LaGarSo _ 2003






