PDF (Levantamiento planimétrico de un terreno con linderos y

61
V-
LEVANTAIHENTO PI,AN HlBTRICO DE
UI~
TERREJIO CON
1INDERCS y DBTAlLE :J Er,íPI.EANDC
l ~L
TEODOLITO Y
l ,A CINTA.
A.
Objeto.
Este tipo de trabajo es el m6s frecuente en la topogra-
fía.; aunaue los trabajos ejecuta.dos con la cinta
o con brú-
jula. y cinta., da.n como resultado el poder confeccionar un
plano del terreno, las limitaciones ya mencionadas de estos
implementos, hace que su uso no sea. el mas 8consejable.
•
Es-
te. práctica introduce el manejo del teodoli to, a-parato fundamental en le topografía..
Teniendo en cuenta. que la medida.
de los á.ngulos, juega un papel ta.n importante como la medida.
de las distancias.
B.
Consideraciones generales.
Es ra.ro, en la. vida. práctica, que el lindero de un terre-
no esté desprovisto de obstáculos físicos que permitan no solo el estacionemiento de a.parato (teodoli to, brújula, etc.)
en los respectivos v'rtices, sino la medida de le distancia
entre los puntos que definen el lindero.
An te esta s dificultades hay que proceder de la siguiente ma.nera:
•
Se establece une poligonal cerrada externa, interna o mixta.
lo más pr6xima. posible a le. "poligonal de linderos" de tal ma.nere. que desde los vértices de aquella. se puedan ver y medir
los vértices de ésta.
La poligonal artificial sirve de apoyo
a la otra, por eso se le conoce también, con el nombre de poliFon81 o red de apoyo.
•
62
1,os vértices que definen la poligona.l lindero reciben el nombre de "detalles" a. los cua.les se les dará coordens.das en
funci6n de las coordenadas que restilten para los vértices
( estaciones) de la. poligone.l de apoyo.
Se puede presentar y de hecho se presenta con frecuencia,
el tener que localizar accidentes nRturales del terreno (quebradas, ríos, etc.)
° e.rtificial es
(casas, Ví8 s, cercos, etc.),
una. y otra clase de accidentes suelen también recibir el nom•
bre de
detall~s y
su 10ce.liza.ci6n en términos generales se
efectu.e a partir de .la. poligonel de apoyo.
Los detalles pueden ser esenciales o meramente descriptivos,
de acuerdo con lB finalidad a que vaya destinado el levanta.miento.
J,08 primeros, como en el caso de los vértices de ls
"poligonal lindero" deben ser localizados con la misma precisi6n lineal y angu.lar con Que se localizó el vértice correspondiente de lB. poligonal de apoyo (estaci6n).
Los segundos, por ejemplo, los vértices de una casa, pueden
loca.lizarse con una menor precisi6n.
Es de advertir que aquí
las denomina.ciones "Detalles descri pti vos
y
esencisles" t ie ·
nen un valor relativo, pues el detalle esencial
~ en
un tipo
de levantamiento puede ser meramente descriptivo en otro y
.
Vlceversa.
c.
Organiza.ción del tre bejo.
l.
Personel:
1 Instrumentista (operador);
2 cadeneros;
1 trochero •
1 Libretista (anotador);
63
2.
Equipo de trabajo:
Teodoli to t cinta metá.lica, plomada, a.gujas (pines),
jalones, estacas, martillo, puntillas, ma.rcadores,
machete.
El equipo de trabajo
y~
personal dependen del tipo de
levantamiento (Ver Davis, pá.g. 337) •
. ..
'
3.
•
Tra.bajo
de ca.mno:
•
a)
Reaonocimiento del terreno •
b)
Establecimiento de los
v~rtices
de la poligonal
de apoyo (materializándolos por medio de estacas
•
o ma rca s) •
El reconocimiento del terreno
y
la. ma.terialización
de la poligonal de apoyo puede ser simultánea, de
,
a.cuerdo con el levantamiento.
Representan en el de-
sa.rrollo del mismo un ahorro consid erable de tiempo,
pues una adecuada. elecci6n de los puntos facilita.
los trabajos posteriores.
e)
Obtenci6n de los valores angulares y linea.les
necesarios para la poligonal base y la localización de los detalles.
D.
Ej emplo.
Levantamiento de un terreno con linderos y detalles, em-
pleando teodolito y cinta..
l.
Organi~a.ción:
a)
J·oligom!.l base:
ABCDE (mixta:
parte interna y
Tlartp. externa)
64
. 2.
b)
Poligona.l de linderos:
1-2-3-4-5-6-7-8-
e)
Detalles descriptivos:
50, 51 .••.•••• , 58 •
Método de trabajo:
a)
Medidas lineales:
b)
Angulos medidos a. le derecha. e.l minuto.
c)
Acimut de la. línee. AE observada con le. brújula.
d)
Detalles:
~.. étodo
cinte
de radiaci6n (ángulo y distancia)
•
3.
Detos de campo:
Librete, de campo .
la. columna:
esteci6n
28..
"
ángulo derecho
3a.
"
distancie
Página de enfrente:
•
•
gráfiCOS y observaciones •
65
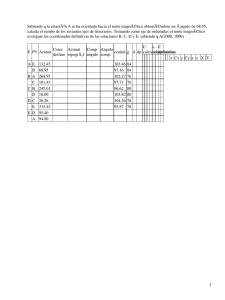
JJIBnETA DE CAMPO
o
Estac.
Obser.
A
E
1_ _ _ _ _ _
-..
,
I
1
2
--IL _ _ _ _ _ -
1- --
,
Angul0
derecho
Distancie
Observa.ciones
m. .
Teodolito : Zeiss-Jena
020 A
Poliaonal
base: ABCDE
,.
"
linderos: 12- 3- .••. 8
Detalles : 50 - 51 ••• 57
Acimut de AE: 72°42'
Portada: ancho 10 mts•
a partir
Punto 2 en dirección 2-1
Ancho de la vía. 6 m.
Puntos 50 - 51- 52- 55:
tomados en el centro de
•
la. vía
-
-
128°25'
- 193°10'
~
-
--
-----_
-
50,80
65,70
..
•
-
-
-- .
__o
50 j 200000' _____ . 46,00
-- 51--- 214°00'
32,00
3 - 286°19'
70,20
1
-
•
--
-
-
,•
,
-
-
-
161,80
17,50
295°17'
328°30'
B
52
-
- -
,
-
B
A
00°00'
225°40
-
4
----
5
----
-- - ;:y
--
-
-
..--
258°31'
277°20'
-
~--
- -
-
.
----
55 .
D
C
--+-- - -
-., o .
I.
/
.
,
00°00'
6
5J. °30'
122°15' 7
. 53 -- 155°00' -
o
,~---
- 200 °00'-----
54
E
---
211 °16
.
....
- -
-
--
... -
-
A
o
-
-~
--
-
8
55
.
. -_.....
D
-,I .-
56
57._-
00°00'
68°30'
153°00'
190°24'
236°00'
350°00'
-
- .,
• !
••
83,80
79,30
35,00
56,00
86,40
-
.
57
51,80
-
- - -1--
,
1j'- ---' -5'
1(;)1,30
178,21
D
- -
E
Puntos 56-57 parqueadero
85,90
B
C
•
--
e
o
,•
.
---
~.
-
-
-
.. -
-
69,00
34,00
95,52
19,00
17,00
-
•
J
Los datos de los detalles descriptivos no se pasen en la hoje
de cálculos por no ser necesario obtener va.lores de coordene.das de estos puntos.
66
4.
Trabajo de oficina:
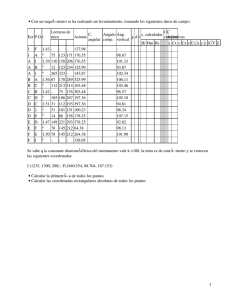
Nota: Todos los valores Que se van obteniendo se
anota.n en las columna.s correspondientes de la hoja
de cálculos (págin8. 82 ) •
a)
Error angu18r de cierre.
Compensación angular.
Como se midieron ángulos exteriores, hacemos
le.s o'Peraciones para esos ve.lores angulares.
Suma. de ángulos exteriores (derechos) observa•
dos
A
A:
1"-
B:
A
295"17'
277-20'
C:
285-40'
/'
D:
211 0 16 '
E:
190 0 24'
L Al =1.259
0
57'
Suma te6rica:
1.260°00'
Error angu1a.r: - 00°03'
:Para compensar este error sumamos:
l' a los
ángulos A, D Y E, escogidos alazar, quedendo:
¡\
A:
0
295 18'
/'-
B:
/'-
c:
/'
277°20'
0
285 40'
D:
211°17'
/'.
190 0 25'
E:
1.260°00'
••
Suma. de ángulos exteriores corre gidos
67
b)
C{:lculo de los Acimu ts de los e j es de la. poligonal base.
Se aa.lculan en función de un a.cimut inicia.l y
d e los ángulos a. la. derecha corregidos, teniendo en cuenta la.s siguientes norma.s:
l.
Se toma como acimut inicial el de una línea
"a.trás" •
•
2.
El acimut de la. línee inmediata. ha.cia. adelante es igual al acimut anterior más el ángulo
horizonta.l derecho formado por los ejes considerados.
El acimut obtenido puede ser menor o nayor
que 180°00'.
Si es menor se le suman 180°00'
y al resultado se le suma el correspondiente
ángulo derecho, obteniendo el acimut de la
línea
sigu.iente,
Si es ma.yor se le restan
180°00' Y se le suma. el ángulo derecho que
corresponde, obteniendo el acimut de la. línea
siguiente (se resta. 360°00' en ca.so de que
°
el ve.l r s ea. IDa.yo r) •
Se repiten las operaciones hasta volver e la
f
línea de partida.•
En el ejemplo qUE' estamos desarrollando ten-
dríamos:
68
Acimut línea atr8s AE :
+ ángulo derecho en A corregido:
370'00' (-360°00)
10°00'
Acimut Línea ÁB
Menor de 180°00' se le suman
190°00'
277°20'
+ á.ngul0 derecho en B corregido:
467°20' (- 360 0 0C)' )
•
Acimut línea. BC
107°20'
Menor de 180°00' se le suman
180°00'
-
287°20'
285°40'
+ á.n gulo derecho en C corregido:
573°00' (-360°00')
Acimut línea CD:
213°00'
Mayor de 180°00' se le resta.n
180°00'
33°00'
+ Angulo derecho es D corregido:
211°17'
Acimut JJínea. DE:
244°17'
Ws.yor 180°00' sele
restan:
-
180°00'64°17'
(
-
+ á.n e;ulo derecho en E corregido:
190°25'
Acimut Línea. EA
254°42'
Calculamos
el~imut
254°42' - 180°00'
de AE como chequeo
= 74°42'
~acirnut de salida y de
11 ega.da. igu,a.l es) •
(
lO 7/120 1
,
l /v
."--•
2 7'70..,
. / (0;
'V
69
y
/ 'Jo '(Jo •
I
I
I
I
•
I
'c
,
b
•
ID
•
~
.
A
ZCf5/1 IK'
GRAFICO l.
c)
Acimuts de la. poligonal base.
cálculo del acimut de las línea.s Estaci6n-Lindero:
Se pueden ca.lcular al mismo tiempo que el de la.
línea. del vértice correspondiente, sumando según
el ceso el á,n gulo derecho de la línea estaci6n
lindero.
-}/
Ejemplo A-l
Acimut línea atrás AE:
74°42'
+ ángulo derecho AEl
1¿8025'
Acimut A-l
203°07 '
-
74°42'
A-2
+ ángulo derecho
-
AE~
Acimut A-2
193°10'
267°52'
- B-4
Línea AB
Menor de 180°00' se le
suman
180°00'
190°00'
+
ángulo derecho BA4
Acimut B-4
•
225°40'
415°40' (-360°00')
5~ 40)
70
B-5
+ ángulo derecho
0
190 0 00'
258 31'
BA5
448°31
(-360°00')
Acimut B-5
.,-
--
D-6
Acimut Línea CD
Mayor del 180°00' se le
restan
33°00'
•
°
+ ~ngulo derecno DC6
51 30 '
Acimut D-6
84°30'
y así para 18.S dem's 1ínea.s
v~rtice
detalle.
B
,
2
-_-.--¡..-¡~\
1
l'
f.O
Al
J.f:,7
'
"
:.J
Z:
-
,~.~ .. 113 '10
GRAFICO 2.
d)
Acimut Linea Estaci6n-Lindero.
Cálc1.J.lo de los rumbos:
Se efectúa a. pa.rti r de los acimuts.
Ejemplo:
Acimut AB
-
I
Rumbo AB:
71
•
Acimut A-l
20)°07';
Rumbo A-l: S 23°07' ~
Acimut E-8
132°47';
Rumbo E-8
S 47°13' E
Etc.
Se puede tra.bajar también con los rumbos ;{ obtener
sus va.lores di rectamente, a. pa.rtir de un rumbo
inicia.l y los ángulos a. la. derecha corregida.
Ejemplo:
•
-
Rumbo AE:
N 74°42' E
Rumbo EA:
S 74°42' W
Rumbo AB:
(acimut 74°42')
74°42' + 295°18:
Rumbo AB:
370°00'
N 10°00' E
Rumbo A-l
74°42' t 128°25' : 203°07'
Rumbo A-l:
y
S 23°07' W
así para los demás.
-
~
-C-o
/
/
,
,I
DI
0
----7:'
1" - , ,
•
GRA FICO 3.
Cálculo de los rumbos.
I
,I
•
I
72
e)
cálculo de la -poligonal base:
l.
Cá.lculo de las proyecciones.
Se busca en las ta.blas el seno y el cosenó '
I
correspondientes a.l valor angular del Rumbo,
•
para. ca.da. lado y se anotan en la. columna respectiva. de la. hoja. de cálculos (pág.82 ),
Se multiplica la distancia. por el seno, obteniéndose la proyecci6n de ese lado sobre el
eje E-W (I,ongitud);
•
al multiplicarla. por el
coseno, se encuentra. la proyecci6n sobre el
ejeN-S (La.ti tUd).
Estos valores se anotan en
la.s columna.s de proyecciones (Pág.82).
Ejemplos:
AB:
Dista.ncia.: 161,80 m.
0
Rumbo: N 10 00' E
Seno Rumbo: 0.173648. Coseno Rumbo: 0.984808
AB: 0.984808 x 161,80
=
Longitud AB: 0.173648 x 161,80
=
~Kitud
159,34 S (-)
Y asi para los demás lados.
Si se tre.be je con calculadora que tenga funciones puede no ser necesario llenar las columnas
de seno y coseno.
Sin emba.rgo, estos va.lores
es conveniente anotarlos para. posteriores chequeos o si le persona. o entidad pare. la. cual
se ejecuta el tra.ba.jo considera que se deben
anotar (ver pág. 80).
2.
Cálculo del error lineal de cierre y de la. presici6n linea.l.
73
En el polígono ABCDE debe cumplirse:
~ Lati tud N = ?
Lati tud S o
~ I,ongi tud E= ~ Longi tu.d
°
oLLongi tud = °
L
La.titud =
Debido a los errores cometidos en el campo,
estas igua.ldades no se cumplen.
1"n ele j emplo:
-
L
•
Longitud E
L Longi tud
L.
W
Longitudes
L T,ati tudes
N
/._ La.ti tudes S
L
--
198,22
-
198,18 ID.
--
La.ti tudas:
ID.
0.04 m.
+
159,34 ID.
159 t 26.m.
0,08 m.
+
J
Error lineal de cierre: \/ 0,04 2 + 0,08 2 =
0,089 m.
=
e
Precisi6n lineal: P
Perímetro:
p
,
=
1
P
572,94 ID. =
:P/e
1
1
=
573,73/0,089
6.446
Si la. precisi6n obtenida está dentro de la tolerancia dispuesta para el trabajo, se continúa.n los cálculos.
Si no sucede ésto, se re-
visan todas las operaciones efectuadas, para
encontrar posibles errores de cd.lculo.
\
Si el
error persiste es necesa.rio chequea.r el tra.ba.jo de cempo.
3.
A juste de la. poligona.l
yecciones.)
~
correcci6n de las pro-
74
Existen varios métodos para, repartir el error
de cierre y hacer que las proyecciones den
sumas igue.les:
Método personal de le. brúju-
la, del teodolito, Crandall, etc. (Davis, Pág.
469-73;
8.
Torres N.Pg.40).
En el ejemplo para. la correcci6ri de las
longitudes emplearem9s el método personal
~equeño
por ser muy
el error (+ 0,04 m.)
•
Tendremos:
Correcci6n para AB:
•
"
It
0,00 m.
BC: -0,02 m. por ser la
ma.yor proyecci6n
•
pe.ra CD
Correcci6n
•
0,00 m•
••
Correcci6n pare DE:
0,01 m.
Corrección pa.ra. EA:
0,01
ID.
-0,04
ID.
Total:
Quedando:
Longitud AB:
+ 28,10
Longitud BC:
+170,10
l ,ongi tud CD:
-
Longitud DE:
- 77,85
Longitud EA:
- 92,14
2:
b.
Long W:
28,81
198,20 m.~Long. E:
198,20
ID.
Para la corrección de les latitudes emplearemos el método de le. brújUla Que re1aciona el error cometido en la.s proyecciones,
la medida lineal del eje y el
perím~tro
de la poligonal.
Corrección pe.ra latitud de AB:
CAB
75
Medida lineal: 161,80 m. Perímetro: 573,73
\
Error en latitud: + 0,08 m.
ID.
Latitud AB:
+ 159,34 m.
CAB : 161,8 m. x 0,08 m.)
0,02
-
ffi.
573,73 m.
Lat. corregida. AB: +159,34 m. - 0,02 m.=
159,32 m.
Corrección para latitud de Be:
•
Medida lineal:
CBC --
177,42
178,21 m. x °z08
573,73
•
CBC
-
ID.
0,02
ID.
ID •
JJat. corregida BC - 53,12
- 0,02
ID.
53,14
Corrección para latitud de CD:
Medida lineal: 51,80
CCD =
ID.
CeD
ID .
51,80 m. x 0,08 m.= 0,007
573,73
-
ID.
ID.
aprox .
0,01
ID.
Lat. corregida CD: 43,44
0,01 m. =
ID. -
43,45
Corrección pa.ra latitud de D8:
86,40
Medida lineal:
ID.
ID.
CDE
ID.
86,40 m. x 0,08
-
IDT
0,01
rt.
573,73 m.
Latitud corregida DE :
37,49 m. - 0,01
ID.
=
37,50 m.
Corre c ci ón PEl.ra. la ti tud EA:
Medida lineal :
CEA
=
95 ,52
95 ,52 m. x 0,08
573,73
ID.
CEA
ID.
ffi.
-
0,02
ID.
aprox.
1
76
ta.ti tud corregida. EA:
-25,21 m. - 0,02 m. 25,23 m.
)
(-
')-
4.
Latitud N (+) -- 159,32 m.
Latitud S ( -) --
159~. 32
m.
Cálculo de las coordenadas de la. poligonal.base (latitudes y longitudes absolutas).
A pa.rtir de las proyecciones corregidas y asigna.n do a uno de los vértices de la poligona.l
•
unos valores de coordena.das que sean adecuados para el dibujo del pla.no, se calculan las
coordenadas de los demás vértices de la poligonal (procurar que todo el plano quede en
el primer cua.drante).
En el ejemplo coordena.da.s de A:
500,00 N Y
500,00 E.
Coordenadas de B:
•
500,00 E + 28,10 (Long. AB) -
528,10 E
500,00 N + 159,32 (I.a.t. AB)
659,32 N
--
•
Coordenadas de C:
528,10 E + 170,10 (IJong. BC) - 698,20 E
659,38 N +
-53,14 (Lat. BC) -- 606,18 H
Coordenadas de D:
697,44 E + (-27,45)
-
669,99 E
606,57 N + (-43,45)
-
562,73 N
669,99 E + (-77,85)
--
592,14 E
562,65 N + (-37,50)
--
525,23 N
Coordenadas de E:
•
~
j.
77
Coordenadas de A (chequeo):
592,14 + (-92,14)
525,23 + (-25,23)
f)
-
500,00 E
500,00 N
c61cul0 de la poligonAl de detalle S( linderos) :
l.
Cálculo de la.s proyecciones de las línea.s
Estaci6n-I,indero.
,
Teniendo el rumbo y la medida linea.l de ca.da
eje Esta.ci6n-J,indero, se calculan las proyecciones correspondientes.
Ejemplo:
Línea. A-l
Rumbo A-l: S 23 0 07'W
Medida lineal: 50,80 m.
Seno Rumbo: 0,397949
Coseno Rumbo: 0,917408
Longitud A-l: 0,397949 x 50,80
LA1
'''' <1 '-f
=~
I,ongi"lrud A-l : 0,917408 x 50,80 m
=
W (-)
1 'L.-
46,60 S (-)
I,ínea. B-4
Rumbo B-4 : S 55 0 40' VI
Seno Rumbo: 0,825770
Medida lineal: 85,90 m.
Coseno Rumbo: 0,564007
Longitud B-4: 0,825770 x 85,90
= 70,93 w (-)
Latitud B-4 : 0,564007 x 85,90
= 48,45
S (-)
y así para las demás lineas.
2.
Calculo de las coordenada.s de los puntos (vértices) de la poligonal de linderos.
Teni endo 18 s coordena.das de la esta.ci6n de 18.
poligonal
ba.se y la.S proyecciones de la línea.
esta.ci6n-lindero, se calcuJ:an las coordenadas
del punto lindero •
•
•
•
78
Ejemplo:
Coordena.da.s de A: 500,00 N;
Proyecciones A-1:
w (-)
46,60 S(-); 20,22
Coordenadas de 1 :453,40 N
;479,78 E
Coordenadas de D: 562,65 N
669,99 E
Proyecciones D-7:
72,02 S\-)
Coordenadas de 7: 490,63 N
y
~5,
33,20 B (+)
703,19 E
así para los demás vértices (puntos) de la.
poligonal de linderos.
g)
500,00 E
Ver observaci6n Nro.
pá.g. 81.
Cá.lcu10 del á.ree. encerrada por la poligonal de
linderos.
Empleamos el método de coordens.das (De.vis, pág.
491;
Torres, pág. 76 ).
En el ejemplo vamos a emplear 2 formas del método
de coordenadas para tener manera de chequear.
l.
Diferencia de a.bscisa.s por ordenadas.
(EA-Ep ) N:
EA: Abscisa del punto atrá.s (a.nterior)
Ep : Abscisa. de punto posterior (siguiente)
N:
vértice 1:
ordenada del punto (vértice)
(642,78-434t35)(453,28)~
+ 94,477,15
(abséisa 8 - abscisa 2 (ordena.da. 1)
Vértice 2: (480,06-501,25)(497,55)= 10,543,08
(abscisa 1 - abscisa 3) (ordena.da
2)
.
Vértice 3: (434,35-599,03)(570,19)= - 93.898,89
Vértice 4: (501,25-629,37)(707,77)= - 90.679,49
Vértice 5: (599,03-753,40)(661,94)= -102.183,67
•
Vértice 6: (629,37-703,19)(570,76)= - 42,133,50
79
Vértice 7: (753,40-642,78)(490,71)
I
=+
54.282,34
vértice 8: (703,19-480,06)(478,36) = +106.736,46
Doble área.
área.:
=-
83.942,68
--
41.971,34 m
El signo no tiene ningún significa.do.
2.
Diferencia. de ordena.da.s por abscisa.s.
(NA - Np ) E
NA: ordenada del punto a trá.s
(anterior)
Np ) ordena.da. del punto posterior
(siguiente)
(abscisa. del punto)
E
Los resultados aparecen anotados en la ho ja. de
cálculo (pág.82).
Al comparar el resultado de un método con el
I
del otro, se aprecia una mínima diferencia.
( 2 cm 2 ) debido a las aproxima.ciones. En trabajos ordinarios es suficiente emplear el método que al calculista le parezca o el que se
haya convenido previamente •
•
7
h)
Dibujo:
Se dibuj6 la. poligonal base y la de linderos por
coordenada.s.
El acotamiento de los ejes se hizo
cada 60 m.
Los detalles descriptivos se dibujaron por á.n gulo
y dista.ncia.
Se completaron con los datos de la
libreta (ver plano,
•
..
p~g.
83 ) •
I
80
E.
Observaciones.
l.
La poligonal ba.se puede en a.lgunos ca.sos tener puntos
comunes con la. de lindero, cuando en ésta existen puntos donde se pueda estacionar el apara.to y efectuar
lE!.s medida.s con comodidad y precisión.
2.
Para aplicar el método
descri to para. cá.l culo de acimut
•
,
es necesario una buena. organizaci6n de los de.tos de
la poli g onal base y linderos •
•
Sentido de la. medida. del ángulo y sentido de recorrido
de la poligona.l.
3.
Si s e emplean calculadora.s que contengan funciones como las
Fx - 15-17-20-101 Y la.s Texas, no es ne-
Ca~io
cesario el cá.lculo de los rumbos.
,
Pues la. ca.lculadora
de. el valor del seno y el coseno, con su signo, para
·
cua l qUl.er
va.1 or compren d'd
l. o en t re OOy 360°.
Se le in-
troduciría entonces el valor ·angula.r del acimut y se
le pediría la función correspondiente;
el signo con-
que ésta aparezca en el tablero de lectura. indica el
I
cuadrante en que cae el eje (línea) cuyas proyecciones se van a oa.lcula,r.
Ejemplos:
Acimut AB: 10°00'
en la. calculadora Sen 0.173648
Cos 0.984808
Acimut A-2: 267 0 52'
"
Sen 0.999307
Cos 0.037225
Acimut BC:
107°20' en la calculad ora Sen 0.954588
Cos 0.297930
_
81
Acimut EA:
o
254 42 en la. ca.lcU¡adora. Sen -0.964557
Cos -0.263873
Al calcular las proyecciones se tendría en cuenta:
l"royecciones N Y E:
Signo + en la funci6n
S Y W:
Singo - en la funci6n
"
4. El empleo de la. calculadora, tanto como el de compvtado•
res, f8cilita y mejorala,s posibilidades de trabajo •
-
Ahorra tiempo y evita equivocaciones de tipo operacional, paro, es completamente indispensable conocer y dominar todos los métodos normales de c8.1 culo, antes de
pasa,r a, emplea,r estos a:para,tos modernos.
5. La poligona.l de linderos no tiene ningún chequeo.
La
bondad de sus datos depende de la poligona.l base y de
la. precisi 6n con que fueron tomados los valores de la
estaci6n al lindero.
6. En el campo se debe hacer el mayor número posible de
chequeos, especialmente si se traba,ja, en un si tio reti ra. ~o
de la ciudad y donde el regreso se di f icultad,
a demás de avmentar considerablemente los costos.
,
•
.~
~
•
,,·,·,·¡;;,s·o
'\D
.... « . ...
.. ~ ...
1.976
_.: , JU),.JlO -
------
_.1•
i
A ~- [;000
0
0°:
I A-I 1128°25
H
l!
,RUi:"!30 II SE.,O
~i
j_:':]
1
'
11. o " ~
ICOSENO,C!STt..NC. ~ .l<~).
I
',-:--
j
i A-3 'Z86°/9'
l
·0 74°4-2~
t-
-.
II
,~.
70.20
i::
!
!
"º-..!C-B ;000
__.____
0
_11
:[ ::s 7 °20'
00' __
iD-
_.
._ _ -1___ -_- - -_-
\
65.65
/.25
T
1 :_
l!
i
I
..
I
I
:ooooOOL _____10 5-~ol7' ¡ _
l ,;
1--
,
1
___
,
ti ,
L~ -:--
•
I _
11.259°57" _::~.
j
~_
'
---.
'
l.
1
-
L
, anQJ!or : ,rror-
_ __ _
_
0 01
""./
.:.
'
:'
1 _
I•
11
1; 101.21
I
53·/2 -0.02 -0.02~170.IO
I'
1
I
!
!
:
,
I
1
¡
1
i
¡I
- '1
:_
1
!I
11
'
¡
i _
l'
j
!
I
!I
I
!
I
i
,1
'
1 '1
:1
,
i
IL-
I
!
I
i
¡
1
,1
¡5í'~.7_;; : .¡.0.04
I
'1
j,
.
1I
'1
l'
.¡..O.08
I'
I
1
:~
le 698·20 606.1& 1
.
1
53.J4
.
-
i
I
'1
1'
l' - - ;;
-
,1
ll-o.Ó4- ··0.081lL138.20
:'I!
1
1,
!
1
:'rrOf lineol:
!i
0, 089
v/
~
.'
I
1753.4-0 570·76
703./9 14-90·71
525.23
592.1-i
198.20 159·37 IS9.32
¡;
:!
H
!
¡
!!
::
11
+92. J0!l+54-.2n341~
6J.. 9?:f:,7b,
;¡
:
1:
¡
_
8 1~'Jm. 478.36 .17 3743! ~/06.736.4(+24,05.9.26 1
A 500.00500.00/1
'1
1 4 BO. 06 4S 3.28
¡
¡¡
~
r
;
1I
:j
1,I
l'1.
1
1
:;
. - 41
I1
1
1
11
'1
11
J
2A; /. 83.C)';2Gg¡,.f85.:J-/.:?70;
v
i
i"
I v
'
I1
Prc:::s¿n: 1/
'i
:1••
·:1:~
l
'
·1
"
1
j
!l1
;'--
I
.¡
-:=] ..
1\
i
I:!
i+I7/_23 !!-42.133.5D+/29. 004, b~~
I
I
....4-b.87 ~223./~
2/).2.3
I
H
!
•
:
1
1
:
669.g9 562731
I
1;
1.
~
I~Eo- :.;;) i\ ·t":-;;;J) ~
~
'!
L
I
1
(Na-t.~p~ !.~i..._;:' .....\.::. ••~
. '
l'
I
NORTE
I
1
,1
:!
ESTE
DC-'':~ • -- ,,..
11
l·
L
1
"UI;.,-'~:"¡,,,~
'1
I!
1
'1
_
-)28.12,4 Sgg.03 7 0 7.771- 91.7511.90.679,49:;-54-.%1,00.
-154.37 5 629.37 b6/.94!+/37.01¡~J02.183,67:, ~ 86.2'29,98.:
48·45
2.ó2 j
70·93
1
v ...
~
il
II
11
11
l
'
63.2.7847t.36
,1
~
!I
¡ A i 50Q·{)O S 00.00!
li
' ~~
-~
46.72!1+208.43! 1 480.06 453.28 !1-/9·/'3i~91..477.15 ·,- 9.212.35'
2.45,- 21.1912 45&-.35 497.55!-/{6.91¡j-(O.54-3/0g::-50.7731~
70.l.9.. .
1-164.68 3 50/.25'570,/9 -2iO.221¡·93 ,&9&,é9:>'O-S.3 1 2,77}
S9"~2
:1
13 528,10659.32
I1
1
.1
1
1
1I
1:
:!
.
J.OO-O.02l_.Zg./ 0
1
S.
~
,
;
l'
Ir
í
I
1: '
j
__ l~-S :068~3~L __ ! ~?~_/7'!S4_?OI3't'.73332? .6732281 69.001'
I
i 50·(,4 ·..... _~.,
~E-A! ¡ 90°.:'..f'Ji~_'-~1_5.!'42·~7-+·42·\J,.?6.f.557!.2638';'.3 95. 52 11-92.{3 1-25.21 -0.01 -0.02 :
9?/4 (
.~ ;E-D
_ . ::::-.:...._-=------
II 2
(i::!J-Ej)
l'
~ :C-D , 285°..J.Jo¡:,}r'.~lj·2 ' 3°0o'333°00'~'¡:,544639 .25S67/1 5/.80 il-28.2/ -4-3.44 0·00 ·CJ.OJ I
28.2,1
tL3.45
1)
_. I
I
I
!!
:I ~
I
D
e !OOOOOO'L~ ~]:3~OO'!
. :;
I
I I li
I
1
_~ID-s~5Jo3~ _ __ ;)j030'N84°30'~~J_~~961.09581~+ 83.3~i
I
\ i li 6'3.4-/1
8.0.3J.
. - 73.82 1 6
:!IJ2.?~.f: _______ ~55~ /5,' P24"45' t~;AI866-º.lg081.:J3 i 73.30 ji
. I
[11
33.20 I
72.02 '1+ 110.62 ,' 7
,]_[,2/1°/6': )" .~.tP'I7' ;~6-+°ITIJ'.900951 !.43392/ 1 86.+0 1 ~77.g4-I-37.4-9 -0.0/ -0.0/ 1:
77.85 1
1\37-5()
,' ;:
¡ _.. _. .
. Of. TOP06QAflA
o' C"'()Dr;f.:~'''r'\'~
li
/9·94.
i
I1
N.
¡
--~__
1
í!
1I
, ¡]-4 '225~O'
755"40"N55'4D'f!.825770 .564-0071 85.g0¡
=-~B.5 :258~5/' - ~-_==>~go3/' ,NB8°3I'EI.9996651.025886¡ 10/.301,
.
~!B-C !277°20': ~::;~' _~7~20'lj7?'4~·..B1.954S88j.297930¡ 178.21 ¡¡t/70./2 l.i_
1
l'
..
W.
r
l
·
l.
t
)0°00' I
_
"' . ."',-i::.."
16/.80 1!+28.iOfI59.3J
j
CO~p-"'q·S
¡V'
"
*LOrJG. LAr ¡¡ . E.
I'-'t..
I
JOloOI'NoloO/'(:.OI?74.31.99S~4..3
l ' ,1:.,''''''
k'I"~~~'~C·~,·I¡
50.80 :'
65.70 I
¡A-B c95°17' ;':.;~_:~'; .')OOO'INIO!JOo'f.:,f73648J.984~08
1
..
!
li
i
iB ~:B-A :000°00'
L'e'lO:"~o'
" :i,, ___
.
Co:r:t!!o'
1;
_"J3°07'iS23·07'W~26051.919707
__
Ni;.CiO~AL
, ...
. !
.-<
~T.q-2 ~ 1930/CY~ --- ?!jr5Z'S87·52·k~!.~9"93D7.037225
f
•
I
1E(T) ,W(-) . N}), S(-)
l
'1.
I'
1
_,
..
'-'
.
~
"
w,~~~~·-·:
S" .~¡,\=:A ~''-' ..,-' ,,-=-t-.:'_ ~~:;-.:U7
:OSSER\•.-= ~
w
;,o
FACi;LTAC) DE C'ENCiAS I.CRICOLAS
.
_l_.:. ..._~----: .:,~
1
~
I!
6.446
'1
1
.l.R¿ ~
AR ~~
.~~
,~.1
,-
J
,
l
:1
=
4/·971) 3 .....
m2
=
C5.5¿O,22
y2
N
I~
.
I
0\
•
~
I
1'1
r-
/
\
/
~
~
/
I
I/
I
I
1'1
~
\
1'1
\•
\\
\
5Q.
•
"'.
.......
"",,,.
-
~.
' ~~
/I
J
I
I
/
/,.
•
C~ ~'"
/
/
//
/
.
/
.~
.~
'"
' '>"-."
.
~~
,
/
/
/
500 N
/+
/
,
./
/'
~~
~?
/
/'
//
N
~
E
~,
1<J
"~ -
t".
~
( A
"
•
,
./
}7
SOON
~~ ,-'_'_..-'~~'-'~"'--·8
___
Ic¡)-·--~-"'_·-"-'"
.¡:.
o
o
1'1
.I
I
UNIVERSIDAD
1."-1.
SEDE OC
~CUlTAD DE CIENCIAS
NACIONAL
MEDELLlN
AGRICOLAS
CONTIENE : Levantamiento plonimétrico de un lote con teodolito y cinto,
poligonal base,linderos y detalles.
Levanto', Ot Topogrofio
Calculó :
"
..
Dibujo :
.
"
I
ESCALA :
1/1.500
Junio _ 1.976
PLANO N9
3