Aplicación Rotor Rígido Espectro Rotacional

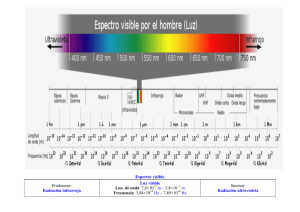
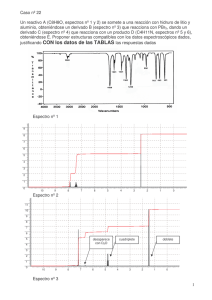
3/19/2014
Aplicación Rotor Rígido
Espectro Rotacional
Ileana Nieves Martínez
QUIM 4042
1
Espectro rotacional de moléculas diatómicas

La energía está dada por:
 l  l  1  2
E 

2I

 J  J  1  2
E 

2I


  L2 
   
  2I 
La degeneración es (2l + 1)

Las transiciones ocurren en el infrarojo lejano y en el microonda.




  L2 
   
  2I 
Requisitos: Dipolo eléctrico permanente-vector del momento de dipolar
eléctrico rota a la misma frecuencia que la molécula.
Ejemplos: HX, CO, CH3X pero no N2, O2, CO2.
Aplicaciones: Radar y horno de microondas.
Reglas de Selección: ΔJ = ± 1 (absorción o emisión)
2
1
3/19/2014
ESPECTRO ROTACIONAL



Energía: E    2I  


Regla de selección: Δ J = ± 1
Transición de niveles de energía para Δ J = +1
 J J  1 2 
  J  1 J  2   2    J  J  1  2 
E
E
E








J 1
J
 J 1
2
I
2I

 


Distribución de Boltzman de poblaciones
N i 

 g exp  
N
i

kT

3
Espectroscopia

Transición en cm-1 para Δ J = +1
h2
2
E  h   J  1 2  2 2  J  1
2I
8 I
hc 2
h2
E    J  1 2  2 2  J  1
 2I
8 I
h
E  1  1
   cm    2 2  J  1  2B  J  1
hc   
8 Ic
4
2
3/19/2014
Espectroscopia: continuación

Niveles de energía de rotación
6B
J=2
4B
2B

J=1
Δσ = 2 B
J=0
Δσ = 2 B
5
ESPECTRO ROTACIONAL

Transición de niveles de energía para Δ J = 1
  J  1 J   2    J  J  1  2 
EJ 1  E J 1  EJ  


2I
2I




2
2

h
2  J   2 2  J 

2I
8 I
2
hc 
h2
E   2  J   2 2  J 
 2I
8 I
E  1  1
h
   cm    2 2  J   2BJ
8 Ic
hc   
E  h 

Para ΔJ = -1:
EJ 1  2 BJ
6
3
3/19/2014
Espectroscopia
Vibro-rotacional
7
Espectro Vibro-Rotacional

Energía y transiciones de vibración y rotación:
 J  J  1  2 
 h  k 
E

En   n  12  


J


2I
 2   
En , J


 h  k 
h2
  n   
  2 J  J  1

2





 4 2 I
1
2
1  h  k  1 h 2
J  J  1
  n   


hc
hc  2    hc 8 2 I
En , J
En , J
hc
1
2
  n  12  e  B J  J  1
8
4
3/19/2014
Espectro Vibro-Rotacional

Energía y transiciones:
En 1, J 1

hc
En , J
 n  1  12  e  B  J  1  J  1  1
   n  12  e
hc
 R  0  2 B  J  1
En 1, J 1
hc
En , J
 BJ  J  1 
J  0,1, 2...
para n  1, J  1
 n  1  12  e  B  J  1  J  1  1
   n  12  e
 BJ  J  1 
hc
 Q  0  2 BJ
J  1, 2,3..... para n  1, J  1

 0 R   1P  4 B
9
Transiciones Vibro-rotacionales
(moléculas diatómicas)
J = -1 (Rama P)
J = +1 (Rama R)
espectro
prohibida
http://www.homepages.ucl.ac.uk/~ucapphj/V
ibrationRotationalSpectrum.gif
10
5
3/19/2014
Formación de la rama P, Q y R
absorción molecular
de excitación
Intensidades reflejan la población
del nivel inicial.
Frecuencia de radiación absorbida
“Physical Chemistry” por P.W. Atkins; Noviembre 1997;
11
W.H. Freeman & Company; 6ta edición
Frecuencia de radiación absorbida
“Physical Chemistry” por P.W. Atkins; Noviembre 1997;
W.H. Freeman & Company; 6ta edición
12
6
3/19/2014
13
“Physical Chemistry” por P.W. Atkins; Noviembre 1997;
W.H. Freeman & Company; 6ta edición
Espectro de alta resolución de HCl
vibración-rotación
Rama - Q
Rama - P
“Physical Chemistry” por P.W. Atkins; Noviembre 1997;
W.H. Freeman & Company; 6ta edición
Rama - R
14
7
3/19/2014
Espectroscopía Raman-Excitación
“Physical Chemistry” por P.W. Atkins; Noviembre 1997;
W.H. Freeman & Company; 6ta edición
15
8