METODOS CUANTITATIVOS PARA ADMINISTRACION
Anuncio

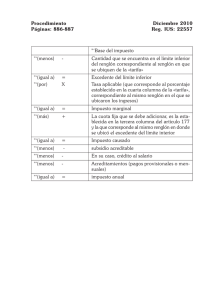
Instituto Tecnológico de Altamira Investigación de Operaciones I METODO SIMPLEX El algoritmo Simplex comprende los siguientes pasos: Paso 1 Se convierte el modelo matemático de Programación Lineal (PL) a su forma estándar. Al elaborar el modelo matemático que representa el problema de PL, tenemos las restricciones que están representadas por desigualdades. El propósito de la forma estándar es eliminar los signos de desigualdad, y representar dichas restricciones en forma de igualdades. Para esto tenemos que agregar variables de holgura (S), restar variables de excedente (E), y usar variables artificiales (A) según sea el caso. Variables de holgura: cuando usamos el signo de ≤ en una restricción, estamos indicando que el lado derecho de la restricción indica el límite superior de dicha variable; es decir, podemos hacer uso de ese recurso hasta agotar la cantidad que indica el lado derecho, incluso ocupar menos, pero no nos podemos pasar de ahí. Entonces, la restricción quedaría así: X1 + 2 X2 + 4 X3 ≤ 300 X1 + 2 X2 + 4 X3 + S1 = 300 Para efectos de interpretación, diríamos que S1 representa el valor que nos faltaría para llegar al límite superior (300), en caso de no haber ocupado la totalidad del recurso, en cuyo caso S1 tomaría un valor de cero. Variables de excedente: el caso contrario de la holgura es el excedente; es decir, cuando tenemos un signo de ≥ en una restricción, nos indica que el lado derecho representa el límite inferior de la variable; o sea que la cantidad indicada ahí es el mínimo que tenemos que cumplir; podemos hacer mas de esa cantidad, pero no menos. Entonces, la restricción quedaría así: 7 X1 + 2 X2 + 3 X3 ≥ 400 7 X1 + 2 X2 + 3 X3 + E1 + A1 = 400 Para efectos de interpretación, diríamos que E1 tomaría el valor con el que excederíamos el límite inferior (400). Cabe mencionar que para efecto de que funcione el método, se necesita implementar una maniobra matemática que consiste en agregar una variable artificial (A) Variables artificiales: dichas variables se implementan solo para lograr que el método matemático funcione. Dichas variables se implementan cuando tenemos una restricción con un signo de = , ya que como el objetivo de la estandarización es que todas las restricciones sean igualdades, cuando nos encontramos una restricción que ya es una igualdad, solo le agregamos la variable artificial. Entonces, la restricción quedaría así: 3 X1 + 1 X2 + 6 X3 = 800 3 X1 + 1 X2 + 6 X3 + A1 = 800 Cabe mencionar que las variables artificiales NO existen, por lo que en definitiva tienen que desaparecer de la solución óptima del problema. Ing. Efraín Padilla Ayala Instituto Tecnológico de Altamira Investigación de Operaciones I Finalmente: Las variables que agregamos a las restricciones del modelo matemático, las tenemos que reflejar en la función objetivo, simplemente agregándolas al cuerpo de la ecuación, tomando en cuenta las consideraciones siguientes: 1. Las variables de holgura (S) y de excedente (E), se agregan con un coeficiente de cero 2. Para las variables artificiales (A), el coeficiente se asignara dependiendo de las características del problema, es decir: a. El coeficiente deberá ser más grande que los valores de los coeficientes de las variables de decisión de la función objetivo (ej. 100) b. El signo de dicho coeficiente deberá ser contrario al objetivo del problema, es decir, si el problema es de Maximización se le pondrá un signo negativo; y si el problema es de Minimización se le pondrá un signo positivo. Paso 2 Se obtiene una solución básica inicial (si es posible) a partir de la forma estándar del PL. Tabla simplex: Variables de la función objetivo Coeficientes de las Variables de la función objetivo Variables Básicas (solución) Cj Cb Valor de las variables que forman la solución del problema Vb Coeficientes de las Variables Básicas (solución) Zj Cj - Zj Renglón para comprobar si la solución es óptima Ing. Efraín Padilla Ayala Valor de la Z Instituto Tecnológico de Altamira Investigación de Operaciones I Paso 3 Se determina si la solución básica inicial actual es óptima. Para determinar si la solución actual es óptima, es necesario calcular el renglón de Zj y el de Cj – Zj, el cual se calcula de la siguiente manera: Es la suma de los productos de todos los elementos de la columna por su valor correspondiente de la columna Cb. Ejemplo: Cj Cb Vb 5 X1 5 0 3 X1 S2 X2 3 1 2 Zj 21 Cj - Zj -16 Zj = (5)(3) + (0)(1) + (3)(2) = 21 Cj - Zj = 5 – 21 = -16 Y para calcular el renglón de comprobación, solo tenemos que efectuar la operación que etiqueta a dicho renglón, es decir: Cj – Zj. Paso 4 Si la solución básica inicial actual no es óptima se determina cuál de las variables básicas actuales se debe volver no básica y cual variable no básica se debe transformar en básica para encontrar el mejor valor de la función objetivo. Para saber si la solución que se presenta es la óptima, es necesario revisar los valores del ultimo renglón (Cj – Zj), y tener en cuenta el objetivo del problema; de tal manera que si el problema es de maximización el problema encontrará su solución óptima cuando los valores del renglón Cj – Zj sean todos negativos o ceros. Y si el problema es de minimización el problema encontrará su solución óptima cuando los valores del renglón Cj – Zj sean todos positivos o ceros. En caso de no ser la solución óptima, se deberá seleccionar una variable para que entre a las variables básicas, y determinar cuál de las variables básicas tiene que salir de la solución. Para determinar que variable va a entrar a la solución hacemos uso nuevamente del renglón Cj – Zj, asi que si el problema es de maximización, la variable que debe entrar a la solución es la que tenga en ese renglón el valor positivo mayor. Y si el problema es de minimización, la variable que debe entrar a la solución es la que tenga en ese renglón el valor negativo mayor. Una vez seleccionada la variable que va a entrar a la solución, debemos dividir (para cada renglón de esa columna) el lado derecho de la restricción entre el valor correspondiente de la columna de la variable que va a entrar, y el renglón que arroje el resultado menor define la variable básica que tiene que salir de la solución. Recuerde que para la siguiente iteración (tabla), hay que hacer operaciones de tal manera que la columna de la variable que entro a la solución quede con un 1 (uno) en la posición donde se cruzan el Ing. Efraín Padilla Ayala Instituto Tecnológico de Altamira Investigación de Operaciones I renglón de la variable que va a salir, y la columna de la variable que va a entrar, y todos los demás elementos de dicha columna deben ser ceros. Paso 5 Encontrar el mejor valor de la función objetivo y volver al Paso 4. Una vez teniendo los valores de la columna de la variable que entro a la solución de la manera en que se describió (toda la columna en ceros, solo donde se cruzan el renglón de la variable que salió y la columna de la variable que entro debe haber un uno), calcular nuevamente los renglones Zj y el de Cj – Zj para comprobar si se llego a la solución óptima. En caso de no ser la solución óptima, regresar al paso 4. Ing. Efraín Padilla Ayala Instituto Tecnológico de Altamira Investigación de Operaciones I CASOS ESPECIALES EN LOS PROBLEMAS DE PROGRAMACION LINEAL (METODO SIMPLEX) 1. 2. 3. 4. Degeneración Óptimos alternativos Soluciones no acotadas Soluciones inexistentes (no factibilidad) DEGENERACION Al aplicar la condición de factibilidad del método simplex, se puede romper un empate en la razón mínima arbitraria. Cuando se presenta un empate, al menos una variable básica será cero en la siguiente iteración, y se dice que la nueva solución es degenerada. Desde el punto de vista práctico, la condición indica que el modelo tiene al menos una restricción redundante. Se dice que un programa lineal es degenerado si una o mas variables básicas tienen valor a cero. Ejemplo solución óptima degenerada: Max Z= 3x1 + 9x2 Sujeto a. X1 + 4x2 <= 8 X1 + 2x2 <= 4 SOLUCIONES ÓPTIMAS ALTERNATIVAS Cuando la función objetivo es paralela a una restricción obligatoria (es decir, una restricción que satisface como ecuación en la solución óptima), la función objetivo asumirá el mismo valor optimo, que se llama óptimos alternativos, en más de un punto de solución. NO ACOTAMIENTO El método simplex identifica en forma automática cualquier no acotamiento que exista, antes de llegar a la tabla simplex final. Lo que sucede es que la regla para determinar la variable que se debe eliminar de la base no funciona. Es decir, cuando los valores para hacer la división correspondiente y determinar la variable que sale son todos negativos o ceros. NO FACTIBILIDAD Se puede reconocer la no factibilidad cuando el criterio para detener el procedimiento señala que ya se ha llegado a una solución óptima y alguna o más de las variables artificiales siguen estando en la solución con un valor positivo. Ing. Efraín Padilla Ayala