Módulo 1 - Web del Profesor

A.Paniagua-H.Poblete
Física 21
Magnetismo
Módulo 1
Campo Magnético
Los imanes son capaces de atraer pequeños pedazos de hierro.
Presentan dos polos uno llamado Norte y otro llamado Sur.
Si el imán está ubicada de tal manera que pueda girar se orientará de tal
forma que su polo Norte apunte hacia el Norte geográfico.
Los polos de distinto nombre se atraen.
Los polos de igual nombre se repelen.
Por lo tanto el polo norte geográfico es un polo Sur magnético ya que atrae a
el polo Norte de un imán.
Los polos de un imán son indivisibles.
N
S
N
S
N S
N
S
Si colocamos limaduras de hierro entorno a un imán, éstas se ordenan de
una determinada forma, lo mismo sucede alrededor de un alambre por el
cual circula una corriente.
Por lo tanto un imán y un alambre con corriente presentan en su entorno la
misma propiedad de actuar sobre limaduras de hierro.
Decimos entonces que entorno a ellos existe algo que llamaremos
Inducción
r
Magnética o Campo Magnético y que designaremos por B .
Las líneas que forman las limaduras entorno a los imanes y a los alambres
con corriente representan a las líneas del campo magnético y se denominan
Líneas de Inducción Magnética o Líneas de Campo Magnético. Se les
asigna el sentido saliente del polo Norte y entrante al polo Sur.
Las líneas de campo magnético tienen las siguientes características:
1)
r La tangente a una línea de campo en un punto dado, indica la dirección de
B en ese punto.
1
2) Las líneas de campo se dibujan de tal forma que el número
r de lineas por
unidad de área transversal es proporcional a la magnitud de B .
Donde las líneas están más concentradas el campo magnético B es mayor
que en aquellas zonas donde están las líneas más separadas.
Imán en un Campo Magnético uniforme
Imán en un Campo Magnético no uniforme
Definición del Campo Magnético
Se observar experimentalmente que cuando una carga eléctrica tiene una
velocidad v en la proximidad de un imán o un alambre con corriente, existe
una fuerza sobre ella que depende del valor y dirección de la velocidad.
Los experimentos realizados con diversas cargas móviles con varias
velocidades en un punto del espacio dan los siguientes resultados
correspondientes a la fuerza magnética.
1) La fuerza es proporcional a la carga q .
r
2) La fuerza es proporcional a v .
3) El valor, dirección y sentido
de la fuerza depende de la dirección y
r
sentido de la velocidad v .
2
4) Si la velocidad de una partícula está dirigida a lo largo de una
determinada línea del espacio, la fuerza es cero.
5) Si la velocidad no está dirigida a lo largo de esa línea, existe una fuerza
que es perpendicular a la misma y es también perpendicular a la
velocidad.
6) Si la velocidad forma un ángulo ! con esta línea, la fuerza es
proporcional al sen! .
7) La fuerza sobre una carga negativa es de sentido opuesto, a la ejercida
sobre una carga positiva con la misma velocidad.
Podemos
resumir
estos
resultados
experimentales definiendo
un campo
r
magnético vectorial B dirigido a lo largo
de la línea descrita en el punto 4) y
escribiendo como valor de la fuerza
magnética
r
r r
F=qv!B
(1-T)
Unidades
Tesla =
Weber
Nt
=
m2
amp! m
1 Tesla =10 4 gauss
Representaremos el campo magnético
entrante al plano de la hoja por una x y el
campo magnético saliente del plano de la
hoja por un punto.
Dibuje en la fig la fuerza para cada una de
las
r cargas que se encuentran en el campo
B
Movimiento de una partícula cargada en un campo magnético
Analizaremos las siguientes situaciones:
1) Campo Magnético Uniforme
a) Cuando la partícula penetra perpendicularmente al campo
magnético.
b) Cuando la partícula no penetra perpendicularmente al campo
magnético.
3
2) Campo Magnético No Uniforme
Campo Magnético Uniforme
r
r
a) v es perpendicular a B
!
En este caso estudiaremos el movimiento de un electrón en un campo
magnético uniforme.
!
Ya que la fuerza magnética es
perpendicular a la velocidad, el
movimiento que experimenta el
electrón es un movimiento circular
uniforme.
Tenemos entonces en este caso que
la fuerza centrípeta es producida
por el campo magnético.
Recordemos que :
m v2
FC =
r
Fm = q v B sen !
FC Fuerza Centrípeta.
(2-T)
(3-T)
Fm Fuerza Magnética.
m = masa del electrón
q = carga del electrón.
Ya que FC = Fm y ! = 90° tenemos entonces a partir de las ecuaciones (2-T) y
(3-T) que
v=
qBr
vm
(4-T) r =
m
qB
(5-T)
De estas expresiones vemos que la velocidad de la partícula y el radio de la
trayectoria que describe son proporcionales, por lo tanto las partículas que
posean mayor velocidad girarán en trayectorias circulares de mayor radio.
Encontraremos ahora el período T de dicho movimiento ¿pero recuerdan qué
es período?
4
Período es el tiempo que demora una partícula en dar una vuelta completa.
Frecuencia es el número de vueltas en una unidad de tiempo y corresponde
al inverso del período.
Tenemos que la velocidad angular ! está dada por:
!=
" 2#
=
t
T
y considerando que
!=
v
r
Tenemos que el período T está dado por la siguiente expresión;
T=
2 "r
v
reemplazando v de la expresión (4-T) tenemos finalmente para el período:
T=
!
2! m
qB
(6-T)
De esta expresión vemos que el período no depende del radio de la
trayectoria que sigue la partícula en el campo magnético.
¿Cómo es posible qué suceda esto? Recordemos que la velocidad de la
partícula es proporcional al radio, por lo tanto las partículas que giran en un
radio mayor poseen mayor velocidad y por esta razón es que es posible que
dos partículas iguales que giran en dos trayectorias de distinto radio
demoren el mismo tiempo en dar una vuelta.
En este principio se basa el
Ciclotrón que es un acelerador de
partículas.
Estas
partículas
aceleradas se utilizan posteriormente
para
bombardear
núcleos y estudiarles su estructura.
r
r
b) v no es perpendicular a B
r
Tenemos que en estercaso v forma un ángulo ! con
el campo magnético !B
Consideraremos en nuestro análisis que la partícula
es positiva.
5
Para analizar el movimiento de la partícula
descomponemos la velocidad en dos componentes una
paralela al campo magnético y la otra perpendicular
al mismo.
La componente de la velocidad perpendicular al
campo produce un movimiento circular.
La componente de la velocidad paralela al campo
produce un movimiento vertical uniforme pues la
fuerza es nula en esa dirección.
De la superposición de ambos movimientos
obtenemos que la trayectoria descrita por la
partícula es una hélice.
Campo Magnético no Uniforme
Analicemos ahora el movimiento de una partícula cargada en un campo
magnético no uniforme.
Observando la figura vemos que el
campo representado en la fig. es
más intenso en los extremos y más
débil en el centro tenemos por lo
tanto que se trata de un campo
magnético no uniforme.
Fig. 1
Para analizar la situación consideremos que penetra al campo magnético
una partícula, cargada positivamente, en la posición que se indica en la
figura.
Analizaremos en primer lugar la mitad izquierda del campo magnético, en
ella vemos que la partícula experimenta una fuerza en el sentido que se
indica en la figura. Para encontrar la trayectoria que describe dicha
partícula descomponemos la fuerza en dos componentes una perpendicular
al campo y la otra horizontal.
La componente perpendicular al campo hace que la partícula describa una
trayectoria circular y la componente horizontal de la fuerza hace que acelere
hacia la derecha.
6
Puesto que la fuerza magnética es siempre perpendicular a la velocidad, el
módulo de ésta no puede variar y por lo tanto un aumento de la componente
horizontal de la velocidad implicará una pequeña disminución de la
componente perpendicular al campo magnético.
Recordemos que el radio de la trayectoria circular que describe la partícula
está dado por:
r=
vm
qB
De esta expresión podemos ver que si la partícula pasa a una zona en que el
campo magnético es más débil su radio aumenta, pero por otro lado tenemos
en este caso que la componente perpendicular de la velocidad también
disminuye; si la variación de la velocidad es pequeña comparada con la
disminución del campo entonces el radio de la trayectoria va aumentando.
Tenemos por lo tanto que la
partícula sigue una trayectoria
como se muestra en la fig. 2.
fig. 2
La partícula acelera horizontalmente hasta que la componente horizontal de
la fuerza magnética se hace nula, hecho que ocurre en el punto medio. La
partícula continúa moviéndose hacia la mitad derecha del campo por inercia,
pero en esta parte podemos ver (fig 1) que la componente horizontal de la
fuerza magnética cambia de sentido y comienza a desacelerar el movimiento
hacia la derecha hasta llegar a anular la componente horizontal de la
velocidad.
Cuando eso sucede la partícula comienza a acelerar horizontalmente hacia la
izquierda hasta llegar al centro donde empieza nuevamente a desacelerar,
así este proceso se repite una y otra vez quedando las partículas cargadas
atrapadas en el campo magnético no uniforme.
Analice que sucede si una partícula en lugar de penetrar en el lugar indicado
en la figura lo hiciera de igual forma en la parte de abajo del mismo campo.
7
Un caso de campo magnético no uniforme es el
campo magnético terrestre.
Si hacemos un corte transversal a la tierra, las
líneas de campo magnético se verían como
aparece en la fig.
Debido a ese campo magnético no uniforme es
que las partículas cargadas que vienen desde el
sol quedan atrapadas en regiones del espacio
conocidas como Cinturones de Van Allen.
Estas zonas sirven como escudo protector de la
tierra.
Encuentre alguna explicación para el hecho de que las partículas positivas
quedan atrapadas en un anillo y las negativas en otro.
Fuerza sobre un alambre con corriente
Tenemos un trozo de alambre de
longitud L=l y área transversal A,
por el cual circula una corriente i.
Dicho
alambre
está
ubicado
perpendicularmente
al
campo
r
magnético B .
En la fig. que aparece a la izquierda
se ha dibujado la fuerza magnética
sobre los electrones en movimiento
en el conductor.
Calcularemos ahora la fuerza magnética F que actúa sobre el alambre.
Tenemos que
F = NFe = nVFe = nAlFe
8
(7-T)
donde Fe es la fuerza magnética sobre cada electrón libre en el conductor, N
el número total de electrones en el conductor y n el número de electrones por
unidad de volumen.
Tenemos que la fuerza magnética sobre un electrón libre en el conductor
está dada por
Fe = e vd B sen90°
123 = e vd B
(8-T)
1
Puesto que v d =
j
i
i
y j=
tenemos entonces de (8-T) que Fe =
B
ne
A
nA
Reemplazando esta expresión en (7-T) tenemos que la fuerza magnética que
actúa sobre el alambre esta dada por
F=ilB
Esta expresión podemos escribirla vectorialmente como
r r
r
F=il !B
(9-T)
r
Donde l es un vector a lo largo del alambre y que apunta en el sentido de la
corriente.
En la siguiente fig. se tiene un campo magnético perpendicular saliente al
plano de la hoja.
En el se encuentran ubicados tres
tramos de alambre por los cuales
circula corriente en el sentido que se
muestra en la fig. Dibuje la fuerza que
actúa sobre cada uno de estos tramos.
9
Movimiento de una espira con corriente en un campo magnético
Fig. 3
Fig. 4
Tenemos que la fuerza magnética sobre un alambre con corriente en un
campo magnético está dada por
r r
r
F=il !B
Aplicando esta expresión a una espira tenemos
r
r
F 2 = F4 = ibB sen(90°!" ) = ibB cos "
r
r
F1 = F3 = iaB sen90°
123 = iaB
1
tenemos entonces que
r
!F = 0
r
r
Pero las fuerzas F1 y F3 producen un torque sobre la espira.
r r r
! =r "F
" ! = bF1 sen # = iabB sen #
Si existen N espiras tendríamos entonces que el torque total es:
! = N! " =
Niab
{
Bsen #
µ momento
dipolar magnético
10
(10-T)
Para
escribir
la
expresión
(10-T)
vectorialmente se define
un
vector
momento
r
dipolar magnético µ cuya dirección y sentido
es el que se muestra en la fig. y su magnitud es
NiabB
Tenemos entonces que el torque queda definido por la expresión
r r r
! =µ"B
(11-T)
Energía de una espira con corriente en un campo magnético
Tenemos que:
!U1"2 = #W1" 2
$2
r
r
= % " # d$ = & % " 'd$
$2
W1!2
$1
$2
$1
$2
$2
!U1"2 = % #d$ = % µ B sen$ d$ = &µB cos $ $
$1
1
$1
U1 ! U2 = !µBcos " 2 + µB cos "1
r r
U = !µ B
11
(12-T)
Analizar cuando el equilibrio de una espira con corriente en un campo
magnético es:
a) Estable.
b) Inestable.
c) Indiferente.
Equilibrio Inestable
Equilibrio estable
Aplicaciones del movimiento de una espira con corriente en un campo
magnético
a) Galvanómetro
Hemos citado anteriormente que los aparatos de medida tales como el
voltímetro, amperímetro y óhmetro se basan en un dispositivo que sirve para
detectar corrientes eléctricas llamado galvanómetro.
Ahora veremos que es un galvanómetro y como funciona.
Para entender su funcionamiento analicemos más en detalle el movimiento
de una espira con corriente en un campo magnético.
Veamos que sucede con las espiras que se muestran a continuación cuando
por ellas circula corriente en el sentido que se muestra en la fig.
12
En ambos casos se produce un torque sobre las espiras, pero estos son en
r
sentido contrario. Dicho giro hace que en ambos casos el momento dipolar µ
se alinie con el campo.
Un galvanómetro tiene en su
interior un conjunto de espiras
que se encuentran ubicadas en
un campo magnético producido
por dos imánes como muestra la
siguiente
fig.
Al
circular
corriente por las espiras estas
experimentan un torque, que se
ve equilibrado por otro torque en
sentido contrario producido por
un alambre en espiral ubicado en
el eje de giro de las espiras. Esto
hace
que
la
aguja
del
galvanómetro se equilibre en una
determinada
posición
que
depende de la intensidad de la
corriente aplicada
permitiendo de este modo medir dicha corriente.
Explique ¿qué sucedería si en un galvanómetro no se respeta la polaridad de
corriente indicada en el aparato?
b) Motores eléctricos de corriente continua
Hemos visto en la parte anterior que el sentido del giro de espiras con
corriente en un campo magnético depende del sentido de la corriente que
circula por ellas.
13
fig. a
fig. b
fig. c
fig. d
En las fig. a,b y c se muestra el giro de la espira en un campo magnético. A
la posición d, pasa la espira por inercia. Vemos que en esta posición aparece
un torque en sentido contrario al giro que traía, haciendo que la espira
desacelere y gire en sentido antihorario. Por lo tanto la espira en estas
condiciones esta imposibilitada de dar un giro completo.
Veamos que sucede si cuando las espiras se encuentran en la posición d
cambia el sentido de la corriente.
fig. e
fig. f
fig. g
fig. h
Tenemos entonces que el cambio de sentido de la corriente permite que la
espira realice la otra mitad del giro hasta llegar a la posición h donde
nuevamente debe cambiar el sentido de la corriente para pasar a la situación
indicada en la fig. a e iniciar nuevamente el ciclo.
Hemos visto entonces que la corriente en la espira debe cambiar su sentido
cada medio ciclo. Aqui surge la pregunta ¿cómo puede hacerse este cambio de
tal manera que sea automático y determinado por la posición de la espira?
En la fig. se muestra un corte transversal de un motor.
14
En la fig de la izquierda podemos ver que la corriente fluye desde la parte
negra a la parte blanca de la espira. En cambio en la fig. de la derecha
podemos ver que fluye desde la parte blanca a la parte negra de la espira.
En las siguientes figuras se puede ver las espiras junto con los carbones que
sirven para cerrar el circuito con la batería.
Vista de un motor elemental de corriente continua.
En las figuras anteriores se puede observar las espiras con corriente
ubicadas en un campo magnético en distintas posiciones de su giro.
También se puede observar en ellas los carbones de contacto y la fuente
eléctrica que proporciona corriente a la espira.
15
Problemas
Problema 1. H-33-28(V), 36(N)
ESPECTRÓMETRO DE MASA
La figura muestra un dispositivo
utilizado por Dempster para medir las
masas de los iones. La puerta S es una
cámara en la cual se está efectuando
una descarga en un gas y produce un
ion de masa M y carga q casi sin
velocidad. El ion se acelera mediante
una diferencia de potencial V y rse hace
entrar en un campo magnético B . En el
campo describe un semicírculo y va a
chocar con una placa fotográfica a una
distancia x de la abertura de entrada
dejando ahí su marca.
Demostrar que la masa M está dada por la siguiente expresión:
B2q x 2
M=
8V
Datos
Iones son partículas cargadas obtenidas de átomos que han perdido o
ganado electrones por lo tanto pueden ser positivos o negativos.
M masa del ion.
q carga del ion.
V i = 0 Velocidad inicial del ion.
V diferencia de potencial (dicha diferencia de potencial acelera al ion
hasta una velocidad V f ).
r
El ion penetra con cierta velocidad V f a un campo magnético B y describe
la trayectoria que se muestra en la fig.
¿Diga cuál es el signo del ion para que describa esta trayectoria?
x distancia donde choca el ion y x = 2r
M=?
Plan de Solución
r
Tenemos que la trayectoria que sigue el ion en el campo magnético B y está
determinada por la velocidad que tiene al penetrar en él.
16
Mv 2
por lo tanto qvB =
r
Fm = F c
Considerando que x = 2r tenemos
2Mv
qB
v=?
(1-P1)
x=
La velocidad con que la partícula entra al campo magnético es la velocidad
que adquiere la partícula después de acelerar en la diferencia de potencial V.
Entonces v = vf
Recordemos que !K + !U = 0 y !U = q !V tenemos entonces que
!K = "q #!V
1
2
Mv f ! 12 Mv i = !q(v f ! vi )
2
(2-P1)
2
(
)
ya que v i = 0 pues los iones salen casi sin velocidad y V f ! V i = !V debido
a que los iones aceleran desde un punto de mayor a uno de menor potencial,
tenemos entonces de la expresión (2-P1)
1
2
Mv2 = qV
(3-P1)
de esta expresión podemos obtener la velocidad con la que la partícula
penetra al campo magnético.
Solución
Tenemos entonces de la expresión (3-P1) para la velocidad del ion
v=
2qV
M
reemplazando esta expresión en (1-P1) y despejamos M tenemos:
x 2 q B2
M=
8V
que corresponde a la expresión que nos pedían encontrar en el enunciado del
problema.
17
Problema 2. H-33-25 (V), 38 (N)
Un positrón de 2 Kev se dispara en un
campo
magnético
de
inducción
2
B = 0.10 Weber / m r y su vector
velocidad de 89° con B .
Cerciórese de que la trayectoria será
una
r hélice, con su eje en la dirección de
B . Encontrar el período, el paso p, y el
radio r de la hélice.
P
v
FB
B
r
Datos
Positrón es la antipartícula del electrón por lo tanto posee su misma masa y
magnitud de carga, pero de signo positivo.
m p = 9.11"10 #31 Kg
q p = 1.60 "10 #19 Coul
K = 2Kev K energía cinética del positrón
Kev (Kiloelectronvolts) = 10 3 ev
ev =1. 6 !10 "1 5 Joule y representa la energía que adquiere un electrón
!
cuando acelera en una diferencia de potencial de un volts.
B = 0.10 Weber / m 2 (es un campo magnético uniforme)
! = 89° ! es
r el ángulo que forma la velocidad de la partícula en el campo
magnético B
La trayectoria de la partícula será una hélice, ver apuntes: movimiento de
una partícula cargada en un campo magnético uniforme. El movimiento se
puede descomponer en un movimiento circular y uno vertical.
Período T es el tiempo que demora una partícula en dar una vuelta.
Paso p es el desplazamiento vertical de la partícula en un período de tiempo
T.
r es el radio de la trayectoria circular que sigue el positrón.
18
Plan de solución
B
•En este caso debemos descomponer la
velocidad de la partícula en dos componentes
una paralela al campo magnético y otra
perpendicular al mismo.
v v II
v!
•La componente de la velocidad perpendicular v ! al campo es la que
determina el movimiento circular de la partícula y por lo tanto con ella se
puede determinar el radio.
•La componente de la velocidad paralela v II al campo determina el
desplazamiento vertical de la partícula y por lo tanto con ella se puede
determinar el paso de la trayectoria.
r
r
r
•Recordemos la expresión de la fuerza magnética: F = q v ! B
Tenemos entonces que la fuerza magnética vertical en este caso es nula ya
que la componente paralela de la velocidad forma cero grado con el campo
magnético.
Por lo tanto el movimiento vertical del positrón es un movimiento uniforme.
Solución
Calcularemos en primer término la velocidad con que el positrón penetra al
campo magnético.
2K
K = 12 m v2 entonces
v=
m
v = 2. 7 !10 7 m / seg
!
!
!
2 !m
a) T =
qB
T = 3.6 !10 "1 0 seg
b)
p = vII T = vcos 89°T
p = 0.17 !10 "3 m
c)
r=
m v" m v sen89°
=
qB
qB
r = 1.5 !10 "3 m
19
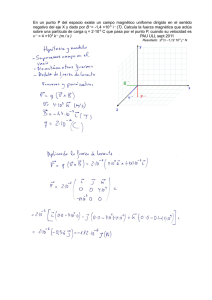
Problema 3
Se tiene un alambre que tiene la forma
indicada en la figura, si por el circula
una corriente i y está ubicado
perpendicularmente
a un
campo
r
magnético B , encontrar la fuerza total
que actúa sobre dicho alambre.
Solución
Subdividimos el alambre en cuatro
tramos y dibujamos en cada uno de
ellos la fuerza magnética.
Tenemos
r
F1 =
r
F2 = !
r
F3 =
r
F4 =
r r
r r
r
F=il !B
l !B
l=a
r
r
r
r
F1 = F2 = F 3 = F 4 = iaB sen90°= iaB
r
F1 ˆj
r
r
F2 cos 30° iˆ + F 2 sen30° ˆj
r
r
F3 cos 30°iˆ + F3 sen30° ˆj
r
F4 ˆj
r
r
r
r
r
r
r
FT = ! F2 cos30°+ F3 cos30° iˆ + F2 sen30°+ F3 sen30°+ F 4 + F1 ˆj
(
) (
)
$
r !
ˆ
ˆ
#
FT = # 2iaB sen30°
123 + 2iaB&& j = 3 iaB j
"
%
1
2
r
FT = 3 iaB jˆ
20