MÓDULO DEL CURSO ACADÉMICO
Anuncio

MÓDULO DEL CURSO ACADÉMICO
ANTENAS Y PROPAGACIÓN
Juan Carlos Vesga Ferreira
Julio César Rueda Rangel
UNIVERSIDAD NACIONAL ABIERTA Y A DISTANCIA
UNAD
Bogotá D.C., 2009
CONTENIDO DEL CURSO
UNIDAD 1: LÍNEAS DE TRANSMISIÓN
Objetivos de la unidad
CAPÍTULO 1. INTRODUCCIÓN A LAS LÍNEAS DE TRANSMISIÓN
1.1 Definición de líneas de transmisión
1.2 Ondas electromagnéticas transversales
1.2.1 Características de las ondas electromagnéticas
1.2.1.1 Velocidad de la onda
1.2.1.2 Frecuencia y longitud de onda
1.3 Tipos de línea de transmisión
1.3.1 Balunes
1.3.2 Líneas de transmisión de conductor paralelo
1.3.2.1 Línea de transmisión de alambre desnudo
1.3.2.2 Línea de transmisión de conductores gemelos
1.3.2.3 Cable de par trenzado
1.3.2.4 Par de cable blindado
1.3.3 Líneas de transmisión concéntrica o coaxial
1.4 Circuito equivalente de una línea de transmisión
1.4.1 Impedancia característica
1.4.2 Constante de propagación
1.5 Propagación de ondas en una línea de transmisión
1.5.1 Factor de velocidad
1.5.2 Longitud eléctrica de una línea de transmisión
1.5.3 Líneas de retardo
1.6 Pérdidas en líneas de transmisión
1.6.1 Pérdidas en el conductor
1.6.2 Pérdidas por radiación
1.6.3 Pérdidas por calentamiento del dieléctrico
1.6.4 Pérdidas por acoplamiento
1.6.5 Efecto corona
1.7 Ondas incidentes y ondas reflejadas
1.7.1 Líneas de transmisión resonante y no resonante
1.7.2 Coeficiente de reflexión
CAPÍTULO 2. ONDAS ESTACIONARIAS Y ANÁLISIS DE LA IMPEDANCIA
EN LÍNEAS DE TRANSMISIÓN
2.1 Definición de onda estacionaria
2.1.1 Relación de una onda estacionaria
2.1.2 Ondas estacionarias en línea abierta
2.1.3 Ondas estacionarias en una línea en corto
2.2 Impedancia de entrada en una línea de transmisión
2.2.1 Adaptación con transformador de un cuarto de longitud de onda
2.2.2 Adaptación con línea de acoplamiento
CAPÍTULO 3. FIBRA ÓPTICA
3.1 Características de la fibra óptica
3.2 Fibra monomodo
3.3 Fibra multimodo
3.4
3.5
3.6
3.7
Ventajas de la fibra óptica
Desventajas de la fibra óptica
Ejercicios propuestos sobre líneas de transmisión
Preguntas
UNIDAD 2: PROPAGACIÓN DE ONDAS ELECTROMAGNÉTICAS
Objetivos de la unidad
CAPÍTULO 4. INTRODUCCIÓN A LA PROPAGACIÓN DE ONDAS
4.1 Propagación de ondas
4.2 Polarización electromagnética
4.3 Rayos y frentes de onda
4.4 Radiación electromagnética
4.4.1 Densidad de potencia e intensidad de campo eléctrico
4.4.2 Impedancia característica del espacio libre
4.5 Frente de onda esférico y Ley del cuadrado inverso
4.5.1 Frente de onda esférico
4.5.2 Ley del cuadrado inverso
4.6 Atenuación y absorción de ondas
4.6.1 Atenuación
4.6.2 Absorción
CAPÍTULO 5. PROPIEDADES ÓPTICAS DE LA ONDA DE RADIO
5.1 Propiedades
5.1.1 Refracción
5.1.2 Reflexión
5.1.3 Difracción
5.1.4 Interferencia
5.2 Propagación terrestre de las ondas electromagnéticas
5.2.1 Propagación de ondas terrestres
5.2.2 Propagación de ondas espaciales
5.2.3 Propagación por ondas celestes
5.2.3.1 Capa d
5.2.3.2 Capa e
5.2.3.3 Capa f
CAPÍTULO 6. TÉRMINOS Y DEFINICIONES DE PROPAGACIÓN
6.1 Frecuencia crítica y ángulo crítico
6.2 Altura virtual
6.3 Máxima frecuencia útil
6.4 Distancia de salto
6.5 Pérdidas en trayectoria por el espacio libre
6.6 Margen de desvanecimiento
6.7 Ejercicios propuestos sobre propagación y ondas electromagnéticas
6.8 Preguntas
UNIDAD 3: ANTENAS Y GUÍAS DE ONDA
Objetivos de la unidad
CAPÍTULO 7. CONCEPTOS BÁSICOS DE ANTENAS
7.1 Introducción a las antenas
7.2 Funcionamiento básico de una antena
7.3 Aspectos fundamentales de las antenas
7.4 Características esenciales de las antenas
7.4.1 Ganancia de antena
7.4.2 Diagrama de radiación
7.4.3 Ancho del haz (beamwidth)
7.4.4 Impedancia de entrada
7.4.5 Polarización de la antena
7.4.5.1 Polarización Vertical
7.4.5.2 Polarización Horizontal
7.4.5.3 Polarización Elíptica
7.4.5.4 Polarización Cruzada
7.4.6 Otras características de las antenas
7.4.6.1 Cociente entre la ganancia del lóbulo principal y el lóbulo trasero
7.4.6.2 Pérdida de retorno
7.4.6.3 Ancho de banda
7.5 Sistemas coordenados o referenciales
7.5.1 Sistema cartesiano
7.5.2 Sistema de coordenadas cilíndrico
7.5.3 Sistema esférico
7.6 Diagrama de radiación
7.7 Resistencia de radiación
7.8 Ganancia directiva y ganancia de potencia
7.8.1 Potencia isotrópica efectiva irradiada
7.9 Densidad de potencia capturada
7.9.1 Potencia capturada
7.10 Abertura del haz de la antena
CAPÍTULO 8. TIPOS DE ANTENAS
8.1 Antenas básicas
8.1.1 Doblete elemental
8.2 Dipolo de media onda
8.3 Antena monopolo o de Marconi
8.4 Conjunto de antenas
8.4.1 Red de radiación lateral
8.4.2 Red de radiación longitudinal
8.4.3 Antena rómbica
8.5 Antenas de uso especial
8.5.1 Dipolo doblado
8.5.2 Antena de Yagi-Uda
8.5.3 Antena de torniquete
8.5.4 Antena log–periódica
8.5.5 Antena de cuadro
8.5.6 Antenas de conjunto enfasado
8.5.7 Antena helicoidal
8.6 Antenas Omnidireccionales
8.7 Antenas Sectoriales
8.8 Antena plana o “patch”
8.9 Antenas de UHF y Microondas
8.9.1 Antena de reflector parabólico
8.9.2 Eficiencia de una antena parabólica
8.9.3 Ganancia de potencia de una antena parabólica
8.9.4 Mecanismos alimentadores
8.9.4.1 Alimentación central
8.9.4.2 Alimentación por bocina
8.9.4.3 Alimentación de Cassegrain
CAPÍTULO 9. GUÍAS DE ONDA
9.1 Tipos de guías de onda
9.1.1 Guía de onda rectangular
9.1.1.1 Frecuencia de corte y longitud de onda de corte
9.1.1.2 Impedancia característica
9.1.1.3 Balanceo de impedancia
9.2 Guía de onda circular
9.3 Guía de onda rígida
9.4 Guía de onda flexible
9.5 Antena de ranura
9.6 La carta de Smith
9.6.1 Graficar impedancias en la carta de Smith
9.6.2 Graficar admitancias en la carta de Smith
9.6.3 Graficar el SWR en la carta de Smith
9.6.4 Cálculo de la impedancia de entrada en una línea de transmisión
Utilizando la carta de Smith
9.6.5 Ejercicios propuestos sobre antenas y guías de onda
9.6.6 Preguntas
Bibliografía
INTRODUCCIÓN
En este módulo muchas descripciones serán cualitativas y otras
cuantitativas ya que los detalles y aplicaciones propios a la ingeniería así
lo exigen para facilitar el proceso de enseñanza-aprendizaje.
El factor clave para la comprensión del presente módulo és el estudio
del electromagnetismo y sus aplicaciones principalmente orientadas
hacia la propagación de ondas electromagnéticas a través de diferentes
medios. El electromagnetismo ha sido la base de la llamada Segunda
Revolución Industrial, fundamentalmente en los aspectos de la
conversión electromecánica de energía y las comunicaciones.
Actualmente las aplicaciones electromagnéticas dominan toda la técnica
moderna y la miniaturización y creciente velocidad de los circuitos
electrónicos hacen cada vez más necesaria la modelación de estos
fenómenos mediante la teoría de campos.
La asignatura denominada “Antenas y Propagación”, es un curso
ofrecido por la Escuela de Ciencias Básicas e Ingenierías de la UNAD,
constituido por 3 créditos académicos correspondiente al campo de
formación Electivo del Programa de Ingeniería en Telecomunicaciones.
Este curso presenta un carácter metodológico debido a que se espera
que el estudiante asimile los elementos conceptuales y los aplique en la
formulación de su proyecto mediante el uso de tecnologías.
El electromagnetismo es una teoría de campos, es decir, las
explicaciones sobre diferentes fenómenos se fundamentan en
magnitudes físicas cuya descripción matemática son campos vectoriales
dependientes de la posición en el espacio y del tiempo. La característica
vectorial dificulta notablemente las resolución de las ecuaciones que
describen el comportamiento, por lo que se trata en la medida de lo
posible de simplificar el problema a ecuaciones escalares, apoyándose
en el uso de herramientas y utilidades de software facilitando con ello
desgaste innecesario de tiempo en la solución de un sistema de
ecuaciones que describen un comportamiento físico.
Este módulo presenta formulaciones analíticas en casos simples que
permiten al estudiante comprender fácilmente cada uno de los temas a
tratar y la forma de interacción de cada uno de ellos aplicado hacia la
propagación de ondas electromagnéticas en el espacio, describiéndose
conceptos y modelos matemáticos simplificados cuando sea posible.
La forma como está concebido el módulo, pretende que el estudiante
comprenda en esencia cada uno de los temas y variables presentes en
éste campo sin llegar a complicarse con complejas expresiones
matemáticas ni llegar a depender absolutamente de un computador para
obtener un resultado sobre algún parámetro de estudio.
Así, una primera parte se ocupa de las líneas de Transmisión y su
comportamiento según la frecuencia de las ondas electromagnéticas a
través de modelos de circuitos cuyos elementos representan diferentes
factores presentes en un sistema de comunicación distribuido, una
segunda parte presenta teoría y aplicaciones sobre la propagación de
ondas electromagnéticas y su interacción con el medio y una tercera
parte presenta los sistemas donde es necesaria la teoría de campos,
como la propagación libre y guiada y la generación de ondas
electromagnéticas fundamentada en el uso de antenas y los parámetros
propios de cada una según su aplicación.
UNIDAD No. 1
LÍNEAS DE TRANSMISIÓN
OBJETIVOS DE LA UNIDAD
Esta unidad propicia que el estudiante adquiera lo conceptos básicos y
comprenda las leyes que rigen el funcionamiento de las líneas de
transmisión y su importancia en el campo de la propagación de señales
electromagnéticas.
Es fundamental que el lector adquiera la comprensión conceptual de los
problemas que deberá enfrentar en aplicaciones de la ingeniería en
telecomunicaciones, así como las herramientas de modelación más
adecuadas
para
las
diferentes
acciones
de
los
campos
electromagnéticos. Por otra parte, se dará énfasis a las aplicaciones
ingenieriles y, cuando sea el caso, a las normas de diseño y seguridad
vigentes en la construcción de sistemas y equipos electromagnéticos.
CAPITULO 1. INTRODUCCIÓN A LAS LÍNEAS DE TRANSMISIÓN
1.1 DEFINICIÓN DE LÍNEAS DE TRANSMISIÓN
Una línea de transmisión es un sistema de conductores metálicos para
transferir energía eléctrica desde un punto a otro. En forma más
específica, una línea de transmisión consiste en dos o más conductores
separados por un aislador, puede tener desde unas pocas pulgadas
hasta varios kilómetros de longitud. Se pueden utilizar para transmitir
señales de corriente continua o corriente alterna. Cuando la frecuencia
de la señal a transmitir es baja, el comportamiento de la línea de
transmisión es bastante sencillo y muy predecible, sin embargo, cuando
la frecuencia de las señales es alta, se complican las características de
las líneas de transmisión su comportamiento es bastante especial.
Figura 1. Línea de Transmisión
Una guía de onda es un dispositivo que se usa para transportar energía
electromagnética y/o información de un sitio a otro. Generalmente se
usa el término línea de transmisión a la guía de onda utilizada en el
extremo de menor frecuencia del espectro. A estas frecuencias es
posible utilizar un análisis cuasi-estático. Para frecuencias más elevadas
la aproximación cuasi-estática deja de ser válida y se requiere un
análisis en términos de campos, que es de mayor complejidad.
Las líneas de transmisión son estructuras de guiado de energía, es
posible considerar a la línea como una sucesión de cuadripolos de
tamaño infinitesimal en cascada. Para cada cuadripolo entonces se
puede aplicar la aproximación cuasi-estática. Esta descripción circuital
se conoce como de parámetros distribuidos.
Uno de los casos de mayor interés, es el caso de las líneas ideales en
donde no existen pérdidas de energía y el cuadripolo exhibe solamente
elementos reactivos.
Resultan ecuaciones de onda para tensión y
corriente a lo largo de la línea, que queda definida por dos parámetros:
la velocidad de propagación de las ondas y la impedancia característica,
que da la relación entre las ondas de tensión y de corriente de una onda
progresiva.
En el caso de las líneas reales se incorporan las pérdidas en los
conductores y en el dieléctrico.
Esto lleva, en el caso de ondas
armónicas, a una constante de propagación compleja que indica la
propagación con atenuación y a una
impedancia característica
compleja. En la práctica son de interés las líneas de bajas pérdidas.
A continuación se presenta una descripción de líneas de uso común. Una
línea cargada generalmente presenta reflexión de potencia, y en el caso
ideal, ondas estacionarias. En general, modificando la impedancia de
carga y la longitud de la línea es posible obtener cualquier impedancia
de entrada, lo que permite usar a las líneas como elementos de
circuito.
Para líneas de transmisión de energía o información, la reflexión
de potencia es habitualmente perjudicial, y está acompañada de
sobrevoltajes y sobrecorrientes en la línea que pueden dañarla.
El parámetro que define usualmente la importancia de la reflexión es la
relación de una onda estacionaria se denomina coeficiente de reflexión
generalizado, el cual se describe como la relación de la tensión de la
onda regresiva y la tensión de la onda incidente en cualquier punto de la
línea.
1.2 ONDAS ELECTROMAGNÉTICAS TRANSVERSALES
La propagación de la energía eléctrica por una línea de transmisión se
hace en forma de ondas electromagnéticas transversales (EMT), en
donde se debe recordar que una onda es un movimiento oscilatorio.
Una onda EMT se propaga principalmente en el no conductor, es decir,
en el dieléctrico que separa a los dos conductores de la línea de
transmisión. Para una onda EMT la dirección del desplazamiento es
perpendicular a la dirección de propagación. Cuando una onda tiene
como desplazamiento la misma dirección de propagación, se le
denomina Onda Longitudinal; un ejemplo de éste tipo de ondas son las
ondas sonoras. Una onda electromagnética EM se produce por la
aceleración de una carga eléctrica. En un conductor, tanto la corriente
como el voltaje siempre están acompañados por un campo eléctrico (E)
y un campo magnético (H) en la región vecina del espacio en donde
éstos campos son perpendiculares entre si en todos los puntos.
Es posible considerar a la línea como una sucesión de cuadripolos de
tamaño infinitesimal en cascada. En el caso de las líneas ideales no
existen pérdidas de energía y el cuadripolo exhibe solamente elementos
reactivos. Resultan ecuaciones de onda para tensión y corriente a lo
largo de la línea, que queda definida por dos parámetros: la velocidad
de propagación de las ondas y la impedancia característica, que da la
relación entre las ondas de tensión y de corriente de una onda
progresiva. Las dos ecuaciones diferenciales ligadas para la tensión y
la corriente a la entrada del cuadripolo son las llamadas ecuaciones del
telegrafista para la línea ideal.
En el caso de las líneas reales se incorporan las pérdidas en los
conductores y en el dieléctrico.
Esto lleva, en el caso de ondas
armónicas, a una constante de propagación compleja que indica la
propagación con atenuación y a una
impedancia característica
compleja. En la práctica son de interés las líneas de bajas pérdidas.
1.2.1 CARACTERÍSTICAS DE LAS ONDAS ELECTROMAGNÉTICAS
1.2.1.1 VELOCIDAD DE LA ONDA
Las ondas pueden viajar a diversas velocidades dependiendo del tipo de
onda y del medio de propagación que se tenga. Una onda sonora viaja
aproximadamente a 334 m/s en la atmósfera normal, en el caso de las
ondas electromagnéticas, éstas pueden alcanzar velocidades muy
superiores a las sonoras; en el espacio libre o vació, las EMT pueden
alcanzar velocidades equivalentes a la velocidad de la luz (3*108m/s),
sin embargo, en la atmósfera terrestre debido a factores como el aire
viajan a menor velocidad y en el caso de una línea de transmisión a una
velocidad mucho menor.
1.2.1.2 FRECUENCIA Y LONGITUD DE ONDA
Una onda electromagnética, es una señal oscilante o variante en el
tiempo, con la característica de ser periódica y repetitiva, lo cual refleja
que posee una frecuencia o rapidez de repetición de la onda.
v
f
c
f
1.3 TIPOS DE LÍNEA DE TRANSMISIÓN
Podemos pensar en una línea de transmisión básica como un par de
electrodos que se extienden paralelos por una longitud grande (en
relación con la longitud de onda) en una dirección. El par de electrodos
se encuentran cargados con distribuciones de carga (variables a lo largo
de la línea) iguales y opuestas, formando un capacitor distribuido. Al
mismo tiempo, circulan corrientes opuestas (variables a lo largo de la
línea) de igual magnitud, creando un campo magnético que puede
expresarse a través de una inductancia distribuida. Así la potencia fluye
a lo largo de la línea.
Las líneas de transmisión se pueden clasificar de dos tipos: balanceadas
y desbalanceadas, en las líneas balanceadas de dos alambres ambos
conductores llevan corriente: el primero lleva la señal y el segundo la
regresa. Este tipo de transmisión se denomina transmisión diferencial o
balanceada de señal. La señal que se propaga por el alambre se mide
como diferencia de potencial entre los dos conductores. La figura 2
muestra un sistema de transmisión balanceado. Ambos conductores de
una línea balanceada conducen corriente de señal, y las corrientes
tienen igual magnitud con respecto a la masa o tierra eléctrica, pero
viajan en direcciones opuestas. Las corrientes que fluyen en direcciones
opuestas en un par balanceado de alambres se llaman corrientes de
circuito metálico. Las corrientes que tienen las mismas direcciones se
llaman corrientes longitudinales. Un par balanceado de alambres tiene la
ventaja de que la mayor parte del ruido de interferencia (que a veces se
llama voltaje de modo común) se induce por igual en ambos
conductores, y produce corrientes longitudinales que se anulan en la
carga. La anulación de las señales de modo común se le llama relación
rechazo de modo común (CMRR, de common-mode rejection ratio).
Siendo comunes las relaciones de 40 a 70 dB.
Figura 2. Sistema de transmisión diferencial o balanceado
Cuando se habla de transmisión diferencial se refiere a que el voltaje
esta presente entre las dos líneas conductores en donde ninguna de las
dos líneas esta conectada al potencial de tierra o nivel de referencia. En
el caso de una línea de una transmisión desbalanceada también se
utilizan dos líneas conductoras con la diferencia que una de ellas si esta
conectada al potencial de tierra o nivel de referencia.
En la transmisión desbalanceada, el conductor conectado a tierra puede
ser también el nivel de referencia para otros conductores portadores de
señal, esto origina a veces problemas debido a que se pueden presentar
inductancias y capacitancias y con ello el surgimiento de pequeñas
diferencias de potencial entre cualquiera de los conductores de señal y
el conductor de tierra; como consecuencia de no tratarse de un punto de
referencia perfecto induciéndose pequeños niveles de ruido en él.
La figura 3 muestra dos sistemas desbalanceados de transmisión. La
diferencia de potencial en cada alambre de señal se mide entre él y la
tierra. Las líneas de transmisión balanceadas se pueden conectar a
líneas desbalanceadas, y viceversa, con transformadores especiales
llamados balunes.
Figura 3. Sistema de transmisión asimétrico o desbalanceado
1.3.1 BALUNES
Cuando se desea conectar sistemas balanceados con sistemas
desbalanceados se requiere de un dispositivo especial denominado
Balún (balanceado a desbalanceado, de balanced to unbalanced). Un
ejemplo clásico de este tipo de situación común es cuando se tiene una
línea de transmisión desbalanceada, como un cable coaxial conectado
con una carga balanceada como una antena mediante un transformador
especial el cual cumple la función de Balún.
A frecuencias relativamente bajas se puede usar un trasformador
ordinario para aislar la tierra de la carga, como se ve en la figura 4ª. El
balún debe tener un blindaje electrostático conectado a tierra física para
reducir al mínimo los efectos de las capacitancias parásitas. Cuando las
frecuencias son relativamente altas se utilizan Balunes de diferentes
tipos según la línea de transmisión. El más común es el Balún de banda
angosta o de CHOKE.
Figura 4. Balunes: (a) balún de transformador; (b) balún de bazuca
Cuando las frecuencias son relativamente altas se utilizan balunes de
varios tipos para líneas de transmisión. El más común es el balún de
banda angosta, que a veces se llama choke, forro o balún bazuca, y se
ve en la figura 4b. Un choke de cuarto de onda se instala en torno al
conductor externo de un cable coaxial y se conecta con él. Así, la
impedancia que se ve hacia la línea de transmisión se forma por el
choke y el conductor externo, y es igual a infinito, es decir, el conductor
externo ya no tiene impedancia cero a tierra. Por lo anterior, un alambre
del par balanceado se puede conectar con el choke sin poner en corto la
señal. El segundo conductor se conecta al conductor interno del cable
coaxial.
1.3.2 LÍNEAS DE TRANSMISIÓN DE CONDUCTORES PARALELOS
1.3.2.1 LÍNEA DE TRANSMISIÓN DE ALAMBRE DESNUDO
Figura 5. Línea de transmisión de alambre desnudo
Una línea de transmisión de alambre desnudo es un conductor de dos
alambres paralelos a corta distancia y cuyo dieléctrico es el aire. Se
colocan espaciadores no conductores a intervalos periódicos para
sostenerlos y mantener constante la distancia entre ellos, esta distancia
entre los conductores comúnmente esta entre dos y seis pulgadas; la
única ventaja que presenta este tipo de línea de transmisión es su
facilidad de construcción ya que debido a la ausencia de blindaje este
sistema presenta altas perdidas por radiación y es muy susceptible al
ruido este tipo de líneas son consideradas como líneas balanceadas.
1.3.2.2 LÍNEA DE TRANSMISIÓN DE CONDUCTORES GEMELOS
Figura 6. Línea de transmisión de conductores paralelos
Los conductores gemelos son otra línea de transmisión de dos alambres
paralelos denominados comúnmente como cable de cinta.
Estos conductores son en esencia iguales que las líneas de transmisión
de conductores desnudos con la diferencia de que los separadores de los
dos conductores son remplazados por un dieléctrico macizo continuo. En
este tipo de líneas de transmisión las distancia entre los dos conductores
es de aproximadamente 5/16 de pulgada y los dieléctricos más
utilizados son el teflón y el polietileno.
1.3.2.3 CABLE DE PAR TRENZADO
Figura 7. Cable de par trenzado UTP
Un cable de par trenzado consiste en dos conductores aislados
enlazados entre si. El trenzado es utilizado para reducir la interferencia
debida a la inducción mutua entre los conductores.
Cada par forma un circuito que puede transmitir datos. La línea consiste
en un grupo de uno o más pares. Esta línea se conoce como UTP
(unshielded twisted pair) y es el tipo más común de línea usada en
redes de computadores. El cable de par trenzado no blindado (UTP) es
un medio de cuatro pares de hilos que se utiliza en diversos tipos de
redes. Cada uno de los 8 hilos de cobre individuales del cable UTP está
revestido de un material aislante. Además, cada par de hilos está
trenzado.
1.3.2.4 PAR DE CABLE BLINDADO
Figura 8. Cable de par trenzado blindado STP
Dentro de las funciones principales de las líneas de transmisión está la
de transportar una señal de un punto a otro idealmente sin pérdida o
atenuación alguna y sin ningún tipo de modificación o interferencia por
tal razón para reducir las pérdidas por radiación e interferencia se
acostumbra en muchos casos encerrar a la línea de transmisión en una
malla de alambre metálica y conductora la cual es conectada a tierra
cumpliendo funciones de blindaje.
Esta malla evita que se irradian señales fuera de ella y evita que
interferencias de tipo electromagnético llegue a los conductores de señal
en conclusión esta línea de transmisión esta constituida por dos
alambres conductores paralelos separados por un material dieléctrico
macizo y toda su estructura encerrada en un tubo conductor integrado
por una malla y finalmente es cubierto con una capa protectora de
plástico.
Comúnmente, con el fin de ofrecer un mayor rechazo a interferencia (en
particular el rechazo a modo común y la diafonía entre líneas) se rodean
los pares con un aislador. Esta línea se conoce como STP (shielded
twisted pair). Tanto UTPs como STPs se usan en instrumentación
electrónica, aviones y otras aplicaciones críticas de transmisión de
datos.
1.3.3 LÍNEAS DE TRANSMISIÓN CONCÉNTRICA O COAXIAL
Figura 9. Líneas de transmisión concéntricas o coaxiales:
(a) rígida llena de aire; (b) línea flexible maciza
Hasta el momento se habían expuesto las líneas de transmisión de
conductores paralelos, las cuales son ideales para aplicaciones con
señales a bajas frecuencias. Sin embargo, en las frecuencias altas, sus
pérdidas por radiación y pérdidas dieléctricas, así como su
susceptibilidad a la interferencia externa son excesivas.
Cuando se desean utilizar líneas de transmisión que brinden excelentes
comportamientos frente a señales de alta frecuencia se recomienda el
uso de conductores coaxiales. Debido, a que permiten reducir las
pérdidas y al mismo tiempo aíslan las trayectorias de transmisión. Un
cable coaxial básico consiste en un conductor central rodeado por un
conductor externo concéntrico a una distancia uniforme del centro. En
esencia existen dos tipos de cables coaxiales comúnmente utilizados
como líneas de transmisión de alta frecuencia: líneas rígidas llenas de
aire o líneas flexibles macizas. Es relativamente costoso fabricar los
cables coaxiales rígidos de aire, y para minimizar las pérdidas, el
aislador de aire debe estar relativamente libre de humedad. Los cables
coaxiales macizos tienen menos pérdidas y son más fáciles de fabricar,
instalar y mantener. Los dos tipos de cable coaxial son relativamente
inmunes a la radiación externa, irradian poco ellos mismos, y pueden
funcionar a mayores frecuencias que sus contrapartes de conductores
paralelos. Las desventajas básicas de las líneas coaxiales de transmisión
son su alto costo y que se deben usar en el modo desbalanceado.
1.4 CIRCUITO EQUIVALENTE DE UNA LÍNEA DE TRANSMISIÓN
1.4.1 IMPEDANCIA CARACTERÍSTICA
Cuando se hace uso de una línea de transmisión en un sistema de
comunicación, muchas veces es importante conocer sus características
eléctricas y la forma como estas interactúan entre si afectando la señal
transmitida. Las características de una línea de transmisión están
determinadas por sus propiedades eléctricas y físicas tales como: la
conductividad de los alambres, la constante dieléctrica del aislamiento
el diámetro del alambre y la distancia entre conductores; estas
propiedades son llamadas constantes eléctricas primarias: resistencia en
corriente continua en serie (R), inductancia en serie (L), capacitancia en
paralelo (C) y conductancia en paralelo (G). Estas constantes primarias
se encuentran distribuidas uniformemente a lo largo de la línea de
transmisión a continuación se explican aspectos importantes a cerca de
las líneas de transmisión.
Figura 10. Línea de transmisión de dos cables paralelos,
circuito equivalente eléctrico
La impedancia de entrada de una línea infinitamente larga a radio
frecuencias es resistiva igual a Ζo. Cuando una onda electromagnética
recorre la línea sin reflexiones, se dice que la onda se propagó por una
línea no resonante.
La relación de voltaje a corriente en cualquier punto de la línea es igual
a Ζo; en donde el voltaje y la corriente incidentes en cualquier punto de
la línea están en fase. Para el caso de una línea, las no resonantes
presentan unas pérdidas mínimas por unidad de longitud.
Toda línea de transmisión que finalice en una carga netamente resistiva
Z
ZO
Z
igual a O se comporta como una línea infinita en donde: IN
, no
hay ondas reflejadas, voltaje y corriente en fase y máxima transferencia
de energía de la fuente a la carga.
La expresión matemática que define la impedancia característica es:
R
G
ZO
jwL
jwC
Cuando se presentan en la línea de transmisión frecuencias bajas, las
componentes reactivas tienden a desaparecer, para lo cual se puede
decir que la impedancia característica es:
R
G
ZO
En caso de presentarse frecuencias extremadamente altas, ocurre el
efecto de que las componentes reactivas son mucho mayores que el
factor resistivo.
ZO
jwL
jwC
L
C
Con base en lo anterior, se puede observar que para el caso de
presentarse señales a muy alta frecuencia, la impedancia característica
de la línea tiende a ser constante e independiente de la frecuencia y la
longitud, dependiendo solamente de los factores inductivos y
capacitivos. Adicionalmente su resultado tiende a ser netamente
resistivo y con ello una absorción total de la energía incidente por parte
de la línea.
Figura 11. Diferenciación de la impedancia característica
En general, La impedancia característica determina, según la Ley de
Ohm, la relación que debe existir entre la tensión y la intensidad en la
línea. La cual se define como la impedancia que se ve desde una línea
infinitamente larga o la impedancia que se ve desde el largo finito de
una línea que se determina en una carga totalmente resistiva igual a la
impedancia característica de la línea.
El concepto de la impedancia característica, representa un valor
uniforme a lo largo de toda la línea, o bien, el valor de la impedancia en
cualquier punto en el caso de no existir señal reflejada, condición que se
cumple cuando la línea tiene una longitud infinita o bien en el caso de
que la impedancia de carga sea exactamente Zo.
Puesto que la
impedancia característica es la misma a lo largo de toda la línea, sus
unidades son de ohms.
La impedancia característica de una línea de transmisión para el caso de
dos conductores paralelos con aire como dieléctrico se puede calcular a
partir de la siguiente expresión:
ZO
276 log
D
r
en donde D r
D Distancia entre los centros de los dos conductores (pulgadas)
r
Radio del conductor (pulgadas)
Ejemplo:
Calcular la impedancia característica de una línea de transmisión en
donde su componentes eléctricas son: L 0.1 H / pie , C 20 pF / pie
Solución:
ZO
0.1 *10 6
20 *10 12
L
C
70.71
Ejemplo:
Calcular la impedancia característica de una línea de transmisión de dos
conductores paralelos con aire como dieléctrico con una relación
D / d 12.22
Solución:
ZO
276 log
D
r
276 log(12 .22 )
300
En resumen, la impedancia característica de una línea depende de la
inductancia de los conductores y de la capacidad entre ellos. Cuanto
mayor sea el diámetro de un conductor, menor inductancia por unidad
de longitud presenta y cuanto mayor es la distancia entre los dos,
menor capacitancia poseen. Por lo tanto dos conductores de diámetro
grande y pequeña separación, tienen impedancia característica baja ya
que L es pequeña y C es grande, por lo tanto, L/C será pequeña. En
forma viceversa, dos conductores de pequeño diámetro y gran
separación tendrán impedancia alta, ya que L será grande y C pequeña
con lo que L/C será grande.
En general la impedancia característica (Z0), de una línea de transmisión
es una cantidad compleja que se expresa en ohms. Involucrando, un
desfase temporal entre la onda de tensión y la onda de corriente, lo cual
implica disipación de energía (resistencia y conductancia) y dispersión
de la señal.
1.4.2 CONSTANTE DE PROPAGACIÓN
La constante de propagación [ ] se utiliza para expresar la atenuación
o pérdida de señal y el desplazamiento de fase por unidad de longitud
en una línea de transmisión. A esta constante de propagación también
se le conoce como el nombre de coeficiente de propagación.
Cuando una señal se propaga a través de una línea de transmisión esta
disminuye su amplitud a medida que aumenta la distancia recorrida.
Cuando una línea es de longitud infinita toda la potencia incidente se
disipa en la resistencia del conductor al avanzar la onda por la línea; por
tal razón, en una línea infinita no regresa o se refleja energía alguna
hacia la fuente.
La ecuación correspondiente a la constante de propagación es:
j
Constante de propagación
Coeficiente de atenuación (nepers por unidad de longitud)
Coeficiente de desplazamiento de fase (radianes por unidad de
longitud)
La constante de propagación se puede expresar en términos de
resistencia, inductancia, capacitancia y conductancia como sigue:
(R
jwL) * (G
jwC)
Como cada distancia igual a la longitud de onda se produce un
desplazamiento de fase de 2
2
A frecuencias intermedias y bajo los criterios wL R y wC G entonces:
R
2 * ZO
G * ZO
2
w LC
Con base en lo anterior se puede decir que la distribución de corriente y
voltaje a lo largo de la línea de transmisión que termina en una carga
igual a su impedancia característica (línea equilibrada) se pueden
calcular de acuerdo a las siguientes características:
I
ISe
L*
V
VS e
L*
V Voltaje en el extremo de la línea donde se encuentra conectada la
fuente
I
Corriente en el extremo de la línea que da a la fuente
Constante de propagación
L Distancia desde la fuente hasta el punto donde se desee calcular el
voltaje y la corriente
1.5 PROPAGACIÓN DE ONDAS EN UNA LÍNEA DE TRANSMISIÓN
1.5.1 FACTOR DE VELOCIDAD
Anteriormente se había hecho mención que las ondas electromagnéticas
viajaban a la velocidad de la luz cuando se propagan en el vació y a una
velocidad inferior cuando lo hacen a través de otro medio; sin embargo,
en las líneas de transmisión metálicas la velocidad varia mucho de
acuerdo al tipo de cable y a la frecuencia de la señal en cuestión.
Uno de los parámetros importantes a tener en cuenta en una línea de
transmisión es el factor de velocidad o constante de velocidad, la cual se
define como la velocidad real de propagación a través de
un
determinado medio con respecto a la velocidad de propagación en el
vació.
Vf
VP
c
Vf
Factor de Velocidad (adimensional)
VP
Velocidad real de propagación (m/s)
C = Velocidad de propagación a través del espacio libre (3x108 m/s)
La velocidad con la que viaja una onda electromagnética en una línea de
transmisión, no solamente depende de las propiedades eléctricas del
conductor sino también de la constante dieléctrica del material aislante
que separa de los dos conductores. Otra forma de expresar el factor o
constante de velocidad según la constante dieléctrica del material es:
1
Vf
R
Todo dieléctrico presenta características inductivas y capacitivas los
cuales afectan la velocidad de propagación de una onda
electromagnética a través de una línea de transmisión.
D
T
VP
D
LC
Si la distancia D se normaliza a 1 m, entonces:
VP
D
1
LC
LC
m/s
Como la longitud de onda, otro de los parámetros de interés en una
onda electromagnética está relacionada en forma directa con la
velocidad de propagación en cuyo caso la expresión para calcular este
parámetro es:
VP
f
c *V f
f
c
f*
R
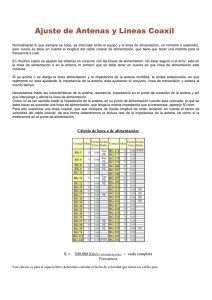
A continuación se ilustran dos tablas correspondientes a los factores de
velocidad y constantes dieléctricas más comunes.
Tabla 1. Factores de Velocidad
Tabla 2. Constantes Dieléctricas
Ejemplo:
Un tramo de línea de transmisión presenta una capacitancia distribuida
C=100pF/m, una inductancia distribuida L=250nH/m. Calcular la
velocidad de propagación y el factor de velocidad.
Solución:
Aplicando la expresión:
VP
1
LC
1
250 * 10
9
* 100 * 10
12
2 * 10 8 m / s
Vf
VP
c
2 *10 8
3 * 10 8
0.66
1.5.2 LONGITUD ELÉCTRICA DE UNA LÍNEA DE TRANSMISIÓN
Otro de los parámetros importantes que describe el comportamiento de
una onda electromagnética a través de una línea de transmisión es la
longitud de una línea de transmisión. A bajas frecuencias (grandes
longitudes de onda), el voltaje a lo largo de la línea de transmisión
permanecerá relativamente constante sin embargo cuando la señal
presenta altos niveles de frecuencia pueden estar presentes varias
longitudes de onda de la señal en la línea provocando con ello cambios
abruptos en el voltaje a lo largo de la línea en consecuencia la longitud
de la línea de transmisión se especifica comúnmente en longitudes de
onda y no en dimensiones lineales. Estos parámetros son aplicables a
líneas de transmisión largas. Una línea de transmisión larga es aquella
cuya distancia sea mayor a un dieciseisavo de la longitud de onda, de lo
contrario se considera una línea corta.
1.5.3 LÍNEAS DE RETARDO
Son aquellas líneas de transmisión diseñadas específicamente para
introducir un retardo de tiempo en la trayectoria de una onda
electromagnética. Este retardo es determinado por las características
inductivas y capacitivas del dieléctrico utilizado. El retardo se calcula de
la siguiente manera.
1.6 PÉRDIDAS EN LÍNEAS DE TRANSMISIÓN
Existen varias formas correspondientes a pérdidas en líneas de
transmisión las cuales pueden ocurrir por los siguientes factores:
pérdidas en el conductor, pérdidas por calentamiento del dieléctrico,
pérdidas por radiación, pérdidas por acoplamiento y el efecto corona.
1.6.1 PÉRDIDAS EN EL CONDUCTOR
Toda línea de transmisión posee internamente una resistencia finita, la
cual provoca pérdidas inevitables de potencia de la señal circulante a
través de la línea. Esta pérdida, es directamente proporcional a la
longitud de la línea, es decir que a mayor longitud mayor resistencia
interna y con ella mayor pérdida de potencia.
Las pérdidas en el conductor pueden variar desde una pequeña cantidad
de decibelios por cada cien metros en cables coaxiales rígidos con
dieléctrico de aire, hasta doscientos decibelios por cada cien metros en
una línea flexible de dieléctrico rígido.
Debido a que la resistencia se distribuye a lo largo de la línea de
transmisión, la pérdida por calentamiento del
conductor
es
directamente proporcional al cuadrado de longitud de la línea.
Además, porque la disipación de potencia es directamente proporcional
al cuadrado de la corriente, la pérdida del conductor es inversamente
proporcional a la impedancia característica.
Una alternativa para reducir las pérdidas del conductor, consiste
simplemente en recortar la línea de transmisión, o utilizar un cable de
diámetro más grande (debe tenerse en cuenta que al cambiar el
diámetro del cable, también cambia la impedancia característica y en
consecuencia, la corriente).
1.6.2 PÉRDIDAS POR RADIACIÓN
Si la separación entre los conductores de una línea de transmisión es
equivalente a una cantidad significativa de la onda, los conductores
pueden llegar a comportarse como antenas enviando y recibiendo
energía debido al comportamiento de los campos eléctricos y
electromagnéticos. La cantidad de energía irradiada depende de la
longitud de la línea, de la frecuencia de la señal, la distancia entre los
conductores y el material dieléctrico que lo separan. Estas pérdidas se
pueden reducir mediante un blindaje aplicado al cable en forma
adecuada.
1.6.3 PÉRDIDAS POR CALENTAMIENTO DEL DIELÉCTRICO
Como entre los conductores de una línea de transmisión existe una
diferencia de potencial y el dieléctrico, como tal, ofrece una resistencia
al paso de la corriente produciéndose con ello un consumo de potencia
reflejado en la línea de transmisión en forma de calor.
Cuando el dieléctrico es aire éstas pérdidas son despreciables de lo
contrario pueden ir aumentado a media que se presenten mayores
niveles de frecuencia en la señal.
1.6.4 PÉRDIDAS POR ACOPLAMIENTO
Este tipo de pérdidas ocurre cada vez que
diferentes líneas de transmisión debido a
eléctricas de cada una de ellas con lo
discontinuidades que tienden a calentar
potencia.
se hace la interconexión de
las características físicas y
cual se establece ligeras
irradiar energía y disipar
1.6.5 EFECTO CORONA
El arco voltaico es una descarga luminosa que se producen entre dos
conductores de una línea de transmisión, cuando la diferencia de
potencial entre ellos es mayor que el voltaje de rotura del dieléctrico
aislante. Cuando éste efecto ocurre la línea de transmisión se puede
considerar prácticamente destruida.
1.7 ONDAS INCIDENTES Y ONDAS REFLEJADAS
En general una línea de transmisión es considerada bidireccional, es
decir, emite la propagación de ondas en ambos sentidos. Cuando la
señal se propaga desde la fuente hacia la carga se denomina señal
incidente, y cuando la señal se propaga de la carga hacia la fuente se
denomina reflejada.
En una línea infinitamente larga, toda la potencia es considerada
incidente y queda almacenada en ella y con esto la no existencia de
potencia reflejada. Si la línea finaliza en una carga netamente resistiva
igual a la impedancia característica de la línea la carga absorbe toda la
potencia incidente considerándose el hecho de una línea de transmisión
ideal sin pérdida.
1.7.1 LÍNEAS DE TRANSMISIÓN RESONANTE Y NO RESONANTE
Cuando en una línea de transmisión no existe potencia reflejada se dice
que ésta línea es no resonante. Adicionalmente se puede obtener el
mismo resultado si la longitud de la línea de transmisión es infinita o si
termina en una carga netamente resistiva de igual valor que la
impedancia característica de la línea.
Cuando la carga no es igual a la impedancia característica de la línea,
parte de la potencia incidente es reflejada nuevamente hacia la fuente si
la carga es un circuito cerrado o abierto toda la potencia incidente es
reflejada hacia la fuente, en otras palabras, una línea resonante es
aquella en la cual la energía es transferida alternadamente entre los
campos eléctrico y magnético de la inductancia y capacitancia
distribuidos en la línea de transmisión, provocando con ello ondas
incidentes y reflejadas.
1.7.2 COEFICIENTE DE REFLEXIÓN
El coeficiente de reflexión es una cantidad vectorial que representa la
relación del voltaje reflejado entre el voltaje incidente.
E REF
E INC
Coeficiente de Reflexión
E INC Voltaje Incidente
E REF
Voltaje Reflejado
CAPITULO 2. ONDAS ESTACIONARIAS Y
IMPEDANCIA EN LÍNEAS DE TRANSMISIÓN
ANÁLISIS
DE
LA
2.1 DEFINICIÓN DE ONDA ESTACIONARIA
Una onda estacionaria deriva su nombre debido al efecto que producen
dando la impresión de permanecer estáticas, es decir, permanecer con
la misma forma en el mismo lugar y solo varían su amplitud. Las ondas
estacionarias presentan mínimos y máximos separados cada mitad de
longitud de onda. Estas ondas se forman debido a la descompensación
existente en una línea de transmisión provocando con ello la aparición
de ondas reflejadas que al interactuar con las ondas incidentes producen
el efecto de la onda estacionaria.
Figura 12. Ejemplo de una onda estacionaria de corriente y voltaje
2.1.1 RELACIÓN DE UNA ONDA ESTACIONARIA
La relación de una onda estacionaria (SWR), se define como la relación
entre voltajes Máximo y mínimo o corrientes máxima y mínima de una
onda estacionaria es una línea de transmisión. Su significado parte de la
descompensación existente entre la impedancia de carga y la
impedancia característica de una línea de transmisión. Su expresión
matemática es la siguiente:
SWR
VMAX
VMIN
Los voltajes máximos de voltaje ocurren cuando una onda incidente y
una onda reflejada se encuentran en fase y los voltajes mínimos ocurren
cuando las ondas incidente y reflejada están desfasadas 180 grados.
Con base en lo anterior, las expresiones matemáticas que permiten
calcular los voltajes máximo y mínimo son:
VMAX
E INCIDENTE
E REFLEJADA
VMIN
E INCIDENTE
E REFLEJADA
Al reemplazar las expresiones anteriores en SWR se obtiene el siguiente
resultado:
SWR
E INC
E INC
VMAX
VMIN
E REF
E REF
Con base en lo anterior se presentan las siguientes dos situaciones
particulares:
E REF
Situación 1:
E INC
En este caso SWR
“Compensación Total”
E REF
Situación 2:
tiende
hacia
el
infinito
denominándose
0
En este caso SWR=1, en donde la impedancia de carga es igual a la
impedancia característica y con ello, MÁXIMA TRANSFERENCIA DE
POTENCIA. Situación que es considerada ideal.
La relación de onda estacionaria SWR también se puede expresar en
función del coeficiente de reflexión
* E INC
SWR
E INC
E INC
E REF
E REF
E INC
E INC
E REF
( * E INC )
( * E INC )
1
1
En casos particulares donde la carga es netamente resistiva, SWR se
puede expresar de la siguiente forma:
SWR
ZO
ZL
SWR
ZL
ZO
Forma No. 1:
Forma No. 2:
Se escoge la que genere como resultado un valor superior a 1,
indicándose con ello que no existe una línea de transmisión equilibrada.
Aunque en la mayoría de las situaciones, las líneas pueden terminar en
una carga que sea equivalente a un circuito abierto o cerrado, se
pueden presentar situaciones no deseadas tales como:
Interferencias de ruido
Generación de imágenes fantasmas por efectos de las ondas
reflejadas
Aumento en las pérdidas de potencia
Aparición del efecto corona por mal estado del dieléctrico
La carga no recibe toda la potencia irradiada desde la fuente
2.1.2 ONDAS ESTACIONARIAS EN LÍNEA ABIERTA
Figura 13. Línea de Transmisión abierta
Cuando se tiene una línea de transmisión en la cual su terminación es
abierta las ondas incidentes de voltaje y corriente no son absorbidas
reflejándose toda la energía de nuevo hacia la fuente de la onda. Las
ondas cuando son reflejadas, mantienen la misma forma que la onda
incidente pero adquieren un desfase de 180º solo para el caso particular
de la corriente. Debido a este efecto se producen sobre la línea de
transmisión ondas estacionarias. Una onda estacionaria presenta un
valor máximo de voltaje en el extremo abierto y un mínimo a un cuarto
de longitud de onda del extremo. Sin embargo una onda estacionaria de
corriente presenta un valor mínimo en el extremo abierto y un valor
máximo a un cuarto de longitud de onda de la abertura.
Figura 14. Ondas estacionarias de voltaje y corriente para una
línea abierta
Las principales características de una línea de transmisión terminada en
abertura son:
la suma de las formas de onda de voltaje incidente y reflejado es
máximo en la abertura
la suma de las formas de onda de corriente incidente y reflejada
es mínima en la abertura
Una onda incidente de corriente se refleja y regresa desfasada
180º
Una onda incidente de voltaje se refleja y regresa sin ningún tipo
de desfasamiento
2.1.3 ONDAS ESTACIONARIAS EN UNA LÍNEA EN CORTO
Figura 15. Línea de Transmisión finalizada en corto circuito
En este tipo de línea, al igual que en el caso de la línea abierta la carga
no absorbe potencia alguna. Sin embargo, en la línea finalizada con
corto circuito ocurre el caso contrario de la línea finalizada en circuito
abierto, produciéndose un desfase de 180º de la onda reflejada con
respecto al incidente para el caso del voltaje; en el caso de la onda
incidente no se produce desfase alguno sobre la onda reflejada.
Figura 16. Ondas estacionarias de voltaje y corriente para una
línea en corto circuito
En el caso del voltaje presenta un valor mínimo en el extremo sobre el
cual se ubica el corto circuito y un valor máximo a un cuarto de longitud
de onda antes del corto en el caso de la onda estacionaria de corriente
presenta un valor máximo sobre el corto y un valor mínimo un cuarto de
longitud de onda antes del corto circuito.
Las características más importantes de una línea de transmisión
terminada en corto circuito son:
La sumatoria de las formas de onda incidente y reflejada de
voltaje sobre el corto circuito es cero
La suma de las formas de onda incidentes y reflejadas de corriente
es máxima en el corto circuito.
La onda estacionaria de corriente se refleja del mismo modo que
si hubiera continuado sin sufrir desfasamiento alguno
La onda estacionaria de voltaje se refleja respecto a la forma en
que continuarían con un desfase de 180º
Uno de los factores que se debe tener en cuenta a la hora de utilizar
líneas de transmisión terminadas en circuito abierto y en corto circuito
es que los valores de reflexión y SWR se encuentran en el peor de los
casos, situación en la cual el coeficiente de reflexión toma como valor 1
y la SWR es infinita.
2.2 IMPEDANCIA DE ENTRADA EN UNA LÍNEA DE TRANSMISIÓN
Uno de los aspectos que hay que tener en cuenta a la hora de realizar el
análisis de una línea de transmisión consiste en la forma como finaliza
ésta línea. Muchas veces puede terminar como un circuito abierto o
como un corto circuito, situación en la cual ocurre una inversión de la
impedancia cada cuarto de longitud de onda.
Provocando con ello que la impedancia de la línea se comporte
resistivamente, inductivamente o capacitivamente según las pérdidas y
los niveles de intensidad de las ondas incidentes y reflejadas.
En la mayoría de los casos, lo que se busca es que la potencia
suministrada por la fuente sea entregada totalmente a la carga; esto
sucede solamente cuando no existe reflexión de ondas caso en el cual la
impedancia de carga y la impedancia característica son iguales. Sin
embargo, esta situación es ideal y siempre existirán ondas reflejadas;
sin embargo, es posible reducir al máximo éstas perdidas y cantidad de
ondas reflejadas realizando acoplamiento de impedancias.
Figura 17. Resumen de impedancias en líneas de transmisión
Existen dos técnicas para realizar el acoplamiento de impedancias:
Adaptación con transformador de un cuarto de onda y adaptación con
línea de acoplamiento.
2.2.1 ADAPTACIÓN CON TRANSFORMADOR DE UN CUARTO DE
LONGITUD DE ONDA
Los transformadores son utilizados comúnmente para hacer acoples de
impedancias y ésta no es la excepción. En el caso particular de las líneas
de transmisión se acostumbra comúnmente el uso de transformadores
de un cuarto de longitud de onda, el cual esta encargado de realizar
procesos de compensación en las líneas de transmisión con cargas
netamente resistivas y de valor diferente a la impedancia característica
de la línea.
Figura 18. Transformador de un cuarto de longitud
Dependiendo del valor de la impedancia de carga, el transformador de
un cuarto de longitud de onda puede comportarse como un
transformador elevador o reductor cuando la impedancia de carga sea
inferior o superior a la impedancia característica respectivamente. Este
dispositivo no funciona dentro de un rango de frecuencias sino en una
sola frecuencia. A continuación se explica el comportamiento del
transformador de un cuarto de longitud de onda según el valor de la
impedancia de carga.
RL
ZO
: El transformador se comporta como un transformador 1:1,
quiere decir, que la señal de entrada es igual a la señal de salida
RL Z O
: El transformador se comporta como reductor
RL Z O
: El transformador se comporta como elevador
Un transformador de un cuarto de longitud de onda, en realidad no es
un transformador sino una línea de transmisión que presenta un
comportamiento semejante al de un transformador. Esta línea o
transformador se conecta entre la línea de transmisión y la carga. La
impedancia característica del transformador de un cuarto de longitud de
onda se calcula de la siguiente forma:
Z TRANSF
ZO * Z L
Z TRANSF
Impedancia característica de un transformador de un cuarto de
longitud de onda
ZO
Impedancia característica de la línea de transmisión
Z L Impedancia de la carga
Ejemplo:
Calcular la longitud e impedancia característica de un transformador de
un cuarto de longitud de onda, el cual se utilizará para compensar una
Z
50
línea de transmisión con impedancia característica O
, con una
carga resistiva de 200Ω y a una frecuencia de 100MHz.
Solución:
Para calcular lo longitud física, es necesario calcular el valor de
lo tanto:
c
f
3 * 10 8
100 * 10 6
4
3
4
/ 4 , por
3m
0.75m
Para calcular la impedancia característica basta simplemente con aplicar
la expresión:
Z TRANSF
ZO * Z L
50 * 200
100
2.2.2 ADAPTACIÓN CON LÍNEA DE ACOPLAMIENTO
Hasta el momento se han analizado cargas netamente resistivas. Sin
embargo, hay casos en los cuales las cargas son inductivas o capacitivas
en su totalidad, situación en la cual no hay absorción de energía, el
coeficiente de reflexión es 1 y a SWR es infinita. En los casos mas
comunes, las cargas presentan cargas resistivas y cargas reactivas
(inductivas o capacitivas), situación en la cual se habla de impedancia
compleja, en donde, es necesario eliminar o reducir al máximo la
componente reactiva para adaptar la línea de transmisión a la carga.
Figura 19. Adaptación con línea de acoplamiento
Una línea de acoplamiento consiste en un tramo adicional de una línea
de transmisión, la cual es conectada entre los hilos de la línea primaria
tan cerca como sea posible de la carga, en configuraciones de línea en
corto o abierta para realizar la adaptación, en donde se prefiere el uso
de líneas en corto debido a que las líneas abiertas tienden a irradiar
energía en presencia de frecuencias alta.
Para adaptar una carga a una línea de transmisión a través de líneas de
acoplamiento en corto es la siguiente:
1. Ubicar un punto tan cerca de la carga como sea posible en donde
Y
el componente inductivo de la admitancia de entrada ENT sea igual
a la admitancia característica de la línea de transmisión
YENT
Donde:
G
jB
G
1
ZO
2. Fijar la línea de acoplamiento en corto a la línea de transmisión en
el punto deseado
3. Realizar el ajuste longitud de la línea según el valor del
componente reactivo en el punto seleccionado.
YENT
G
jB
jB ACOPLADO
YENT
, en donde
B
B ACOPLADO
G
CAPITULO 3. FIBRA ÓPTICA
3.1 CARACTERÍSTICAS DE LA FIBRA ÓPTICA
Figura 20. Fibra óptica y principales tipos de conectores
La fibra óptica es uno de los medios físicos de transmisión más
importantes y utilizados en el mundo debido a las bondades que ofrece
en procesos de comunicación. La fibra óptica está constituida por
filamentos de vidrio (compuestos de cristales naturales) o plástico
(cristales artificiales), del espesor de un pelo (entre 10 y 300 micrones).
Llevan mensajes en forma de haces de luz que realmente pasan a través
de ellos de un extremo a otro, donde quiera que el filamento vaya
(incluyendo curvas y esquinas) sin interrupción.
Las fibras ópticas están reemplazando los
convencionales, tanto en pequeños ambientes
cables de cobre
autónomos (redes
hogareas), como en grandes redes geográficas (Internet y aplicaciones
de voz, video y datos en banda ancha).
El principio que permite enviar una señal a través de una fibra óptica se
basa en la transmisión de luz por reflexión interna total; la luz que viaja
por el centro o núcleo de la fibra incide sobre la superficie externa con
un ángulo mayor que el ángulo crítico, de forma que toda la luz se
refleja sin pérdidas hacia el interior de la fibra. Así, la luz puede
transmitirse a larga distancia reflejándose miles de veces.
Para evitar pérdidas por dispersión de luz debida a impurezas de la
superficie de la fibra, el núcleo de la fibra óptica está recubierto por una
capa de vidrio con un índice de refracción mucho menor; las reflexiones
se producen en la superficie que separa la fibra de vidrio y el
recubrimiento.
La fibra óptica es considerada como una guía de luz y que
adicionalmente en la fibra óptica la señal no se atenúa tanto como en el
cobre, debido a que en las fibras no se pierde información por refracción
o dispersión de luz consiguiéndose así buenos rendimientos, sin
embargo, en el caso del cobre, las señales se ven atenuadas por la
resistencia del material a la propagación de las ondas electromagnéticas
de forma mayor.
La mayoría de las fibras ópticas se construyen de arena o sílice, en
donde se puede decir que ésta materia prima es más abundante y
económica en comparación con el cobre. Con unos cuantos kilogramos
de vidrio pueden fabricarse aproximadamente 43 kilómetros de fibra
óptica.
Cuando se desea transmitir una señal a través de la fibra óptica, se
debe contar con un dispositivo capaz de convertir las ondas eléctricas en
ondas de luz, el cual puede ser un Diodo Emisor de Luz (LED) o un
LASER. Por ello se le considera el componente activo de este proceso.
Una vez es transmitida la señal luminosa por las minúsculas fibras, en
otro extremo del circuito se encuentra un tercer componente al que se
le denomina detector óptico o receptor, cuya misión consiste en
transformar la señal luminosa en energía electromagnética, similar a la
señal original.
Los diodos emisores de luz y los diodos láser son fuentes adecuadas
para la transmisión mediante fibra óptica, debido a que su salida se
puede controlar rápidamente por medio de una corriente de
polarización. Además su pequeño tamaño, su luminosidad, longitud de
onda y el bajo voltaje necesario para manejarlos son características
atractivas.
Los tipos más comunes de fibra óptica son:
3.2 FIBRA MONOMODO:
Son fibras de núcleo pequeño, presentan menor dispersión,
comúnmente utilizada en aplicaciones de transmisión hasta 3Km, utiliza
láser como fuente de luz debido al tamaño reducido del núcleo.
Potencialmente, esta es la fibra que ofrece la mayor capacidad de
transporte de información. Tiene una banda de paso del orden de los
100 GHz/km. Los mayores flujos se consiguen con esta fibra, pero
también es la más compleja de implantar.
Figura 21. Fibra Monomodo
La figura 21, muestra que sólo pueden ser transmitidos los rayos en
línea recta, por lo que se ha ganado el nombre de "monomodo" (modo
de propagación, o camino del haz luminoso, único). Son fibras que
tienen el diámetro del núcleo alrededor de los 10 micrones. Si el núcleo
está constituido de un material cuyo índice de refracción es muy
diferente al de la cubierta, entonces se habla de fibras monomodo de
índice escalonado. Los elevados flujos que se pueden alcanzar
constituyen la principal ventaja de las fibras monomodo, ya que sus
pequeñas dimensiones implican un manejo delicado y generan
dificultades de conexión.
3.3 FIBRA MULTIMODO:
Es un tipo de fibra que presenta un núcleo mayor que el de la fibra
monomodo entre los 50 y 65 micrones, con éstas fibras se presenta una
mayor dispersión de la señal y con ello mayores pérdidas de potencia,
se utiliza comúnmente en aplicaciones de larga distancia pero no tan
largas como las alcanzadas con una fibra monomodo logrando
establecer comunicaciones hasta 2Km de distancia. Debido a que no hay
necesidad de enviar un haz en línea recta, es posible el uso de LEDs
como fuentes de luz.
Figura 22. Fibra Multimodo
Las fibras multimodo de índice de gradiente gradual tienen una banda
de paso que llega hasta los 500MHz por kilómetro. Su principio se basa
en que el índice de refracción en el interior del núcleo no es único y
decrece cuando se desplaza del núcleo hacia la cubierta. Estas fibras
permiten reducir la dispersión entre los diferentes modos de
propagación a través del núcleo de la fibra.
3.4 VENTAJAS DE LA FIBRA ÓPTICA
Su principal ventaja es el gran ancho de banda que ofrece, el cual,
mediante técnicas de multiplexación por división de frecuencias
(WDM/DWDM), permiten enviar hasta 100 haces de luz (cada uno con
una longitud de onda diferente) a una velocidad de 10Gb/s cada uno por
una misma fibra, alcanzando velocidades de transmisión totales de
hasta 10Tb/s.
Otra de las ventajas interesantes es su inmunidad a las interferencias
electromagnéticas.
3.5 DESVENTAJAS DE LA FIBRA ÓPTICA
Dentro de las desventajas ofrecidas por la fibra óptica frente a otros
medios de transmisión se pueden mencionar:
La alta fragilidad de las fibras
Necesidad de usar transmisores y receptores más caros
Los empalmes entre fibras son difíciles de realizar, especialmente
en el campo, lo que dificulta las reparaciones en caso de rotura del
cable
No puede transmitir electricidad para alimentar repetidores
intermedios
La necesidad de efectuar, en muchos casos, procesos de
conversión eléctrica-óptica
La fibra óptica convencional no puede transmitir potencias
elevadas
No existen memorias ópticas
3.6 EJERCICIOS PROPUESTOS SOBRE LÍNEAS DE TRANSMISIÓN
1. Calcular las longitudes de onda para ondas electromagnéticas en el espacio
libre con las siguientes frecuencias: 2 KHz, 150 KHz, 1.2 MHz, 1.5 GHz
2. Calcular las frecuencias de ondas electromagnéticas en el espacio libre que
presentan las siguientes longitudes de onda: 10 mm, 15 cm, 2m, 50m, 2km,
3. Calcular la impedancia característica de un cable coaxial con inductancia L
= 0.2 µh/pie y capacitancia C= 20 pF/pie
4. Calcular el factor de velocidad y la velocidad de propagación en un cable
coaxial con capacitancia C = 50 pF/ m e inductancia L = 240 nH/m
5. Calcular el coeficiente de reflexión en una línea de transmisión con voltaje
incidente de 0.4 V y voltaje reflejado de 0.03V
6. Calcular el parámetro SWR en una línea de transmisión con amplitud
máxima de la onda estacionaria de voltaje de 10v y una amplitud mínima de
onda estacionaria de voltaje de 1V
7. Calcular la SWR para una línea de transmisión de 55Ω y una resistencia de
carga de 70 Ω
8. Calcular la impedancia de característica de un transformador de cuarto de
onda el cual se adapta a una línea de transmisión de 50 Ω y a una carga
resistiva de 65 Ω
3.7 PREGUNTAS
1. Defina los siguientes términos: velocidad de onda, línea de transmisión,
impedancia característica de una línea de transmisión, constante de
propagación, factor de velocidad, coeficiente de reflexión, longitud eléctrica
e impedancia de entrada
2. Explique brevemente que son línea de transmisión balanceadas y
desbalanceadas
3. Explique cuales son las propiedades físicas y eléctricas de una línea de
transmisión, que factores determinan su impedancia característica, su factor
de velocidad y su constante dieléctrica,
4. Haga un cuadro comparativo de una línea de transmisión que termina en
corto circuito y una que termine en circuito abierto ilustrando diferentes
situaciones que se puedan presentar de acuerdo con su longitud
5. Describa que técnicas existen para acoplamiento de impedancias y
explique brevemente cada uno de ellos
UNIDAD 2:
PROPAGACIÓN DE ONDAS ELECTROMAGNÉTICAS
OBJETIVOS DE LA UNIDAD
Esta unidad busca que el estudiante adquiera lo conceptos básicos y
comprenda las leyes que rigen el comportamiento de las Ondas
Electromagnéticas y su propagación en diferentes medios de
transmisión. Se desea que el estudiante adquiera la comprensión
conceptual de los problemas que deberá enfrentar en aplicaciones del
tratamiento de señales electromagnéticas, los parámetros que
gobiernan su comportamiento y su importancia en el campo de las
telecomunicaciones.
CAPÍTULO 4. INTRODUCCIÓN A LA PROPAGACIÓN DE ONDAS
4.1 PROPAGACIÓN DE ONDAS
Anteriormente se describieron las ondas electromagnéticas transversales
y se expuso como los conductores metálicos se pueden utilizar como
medio de transmisión de las señales de un punto a otro. Actualmente,
en los sistemas de comunicaciones basados en frecuencias no es
práctico el uso de hilos para interconectar dos equipos en forma física
debido a las grandes distancias que se deben recorrer para alcanzarse
mutuamente.
La propagación de ondas electromagnéticas por el espacio libre se suele
llamar: propagación de radiofrecuencia (RF); como se menciono
anteriormente, las ondas electromagnéticas en el espacio libre pueden
viajar a la velocidad de la luz. Sin embargo, en la atmósfera se
producen perdidas en la señal que en el vacío no se encuentran, las
ondas electromagnéticas transversales se pueden propagar a través de
cualquier material dieléctrica incluyendo el aire. No obstante, las ondas
no se propagan bien a través de conductores con pérdidas como
ejemplo: el agua de mar debido a que los campos eléctricos en este tipo
de materiales hacen que fluya corrientes que disipan con rapidez la
energía de las ondas.
Las ondas de radio se consideran ondas electromagnéticas como la luz y
al igual que ésta, viajan a través del espacio libre en línea recta con una
velocidad de 300,000,000 metros por segundo. Otras formas de ondas
electromagnéticas son los rayos infrarrojos, los ultravioleta, los rayos X
y los rayos gamma.
Las ondas de radio se propagan por la atmósfera terrestre con energía
transmitida por la fuente, posteriormente la energía se recibe del lado
de la antena receptora. La radiación y la captura de esta energía son
funciones de las antenas y de la distancia entre ellas.
4.2 POLARIZACIÓN ELECTROMAGNÉTICA
Una onda electromagnética contiene un campo eléctrico y uno
magnético perpendiculares entre sí. La polarización de una onda
electromagnética plana no es más que la orientación del vector de
campo eléctrico con respecto a la superficie de la tierra; es decir,
respecto al horizonte. Si la polarización permanece constante se
denomina polarización lineal. La polarización lineal puede ser de dos
tipos: polarización horizontal y polarización vertical. Si el campo
eléctrico se propaga en dirección paralela a la superficie de la tierra se
dice que la onda esta polarizada horizontalmente por otra parte si el
campo eléctrico se propaga perpendicularmente a la superficie terrestre
se dice que la onda esta polarizada verticalmente. Si el vector de
polarización gira 360º a medida que la onda recorre una longitud de
onda por el espacio y la intensidad de campo eléctrico es igual en todos
los ángulos de polarización se dice que la onda tiene polarización
circular; sin embargo, cuando la intensidad de campo eléctrico varia con
cambios en la polarización se dice que es una polarización elíptica.
4.3 RAYOS Y FRENTES DE ONDA
Una onda electromagnética es invisible y difícil de analizar en forma
directa; por tal razón, se deben utilizar métodos alternativos de análisis
para describir su comportamiento y poder realizar un análisis
aproximado de su comportamiento. Los conceptos de rayo y frentes de
ondas son mecanismos alternativos que permiten ilustrar los efectos de
la propagación de ondas electromagnéticas en el vacío.
Un rayo es una línea trazada a lo largo de la dirección de propagación de
una onda electromagnética, son comúnmente utilizadas para mostrar la
dirección relativa de una onda o de múltiples ondas. Un frente de onda
representa una superficie de ondas electromagnéticas de fase
constante; este se forma cuando se unen puntos de igual fase en rayos
que se propagan desde la misma fuente.
Figura 23. Frente de onda producido por una fuente puntual
Una fuente puntual es un solo lugar desde el cual se propagan rayos por
igual en todas las direcciones. El frente de una onda generado por una
fuente puntual se puede representar como una esfera de radio R y su
centro esta en el punto de origen de las ondas electromagnéticas.
4.4 RADIACIÓN ELECTROMAGNÉTICA
Cuando se analiza la radiación electromagnética existe la necesidad de
analizar dos parámetros importantes: densidad de potencia e
impedancia característica.
4.4.1 DENSIDAD
ELÉCTRICO
DE POTENCIA
E INTENSIDAD
DE CAMPO
Las ondas electromagnéticas representan el flujo de energía en la
dirección de propagación, la rapidez con la cual la energía pasa a través
de una superficie dada en el espacio libre se denomina densidad de
potencia; quiere decir, que la densidad de potencia es la energía por
unidad de tiempo y por unidad de área y se expresa en watts por metro
cuadrado. La intensidad de campo es la intensidad de los campos
eléctrico y magnético de una onda electromagnética que se propaga en
el vacío. El campo eléctrico se expresa en voltios por metro y el campo
magnético en amperios por metro.
La expresión que permite calcular la densidad de potencia es:
P
E*H
P Densidad de potencia (W/m2)
E Intensidad rms del campo eléctrico (Voltios/m)
H Intensidad rms del campo magnético (Amperios/m)
4.4.2 IMPEDANCIA CARACTERÍSTICA DEL ESPACIO LIBRE
Las intensidades de campo eléctrico y magnético de una onda
electromagnética en el espacio libre se relacionan a través de la
impedancia característica (resistencia en el espacio vacío). La
impedancia característica de un medio de transmisión sin perdidas es
igual a la raíz cuadrada de la relación de su permeabilidad magnética
entre su permitividad eléctrica y se le denomina como ZS.
ZS
O
O
ZS
O
O
1.26 *10 6
8.85 *10 12
377
Impedancia característica del espacio libre
6
Permeabilidad magnética del espacio libre ( 1.26 *10 H / m )
12
Permitividad eléctrica del espacio libre ( 8.85 *10 F / m )
Con base en lo anterior, aplicando la ley de Ohm se obtiene que:
P
E2
377
377 * H 2
P Densidad de potencia (W/m2)
E Intensidad rms del campo eléctrico (Voltios/m)
H Intensidad rms del campo magnético (Amperios/m)
4.5 FRENTE DE ONDA ESFÉRICO Y LEY DEL CUADRADO INVERSO
4.5.1 FRENTE DE ONDA ESFÉRICO
Figura 24. Frente de onda esférico producido por una fuente isotrópica
La figura 24 muestra una fuente puntual que irradia potencia a una tasa
constante y uniformemente en todas direcciones. Esa fuente se llama
radiador isotrópico. No existe un radiador realmente isotrópico; sin
embargo, se puede aproximar a una antena omnidireccional. Una fuente
puntual irradia potencia en forma constante y uniforme en todas las
direcciones; a esta fuente se le denomina radiador isotrópico. Un
radiador isotrópico produce un frente de onda esférico cuyo radio es R;
todos los puntos ubicados a una distancia R de la fuente tienen igual
densidad de potencia, es decir, que la potencia irradiada esta
uniformemente distribuida sobre la superficie total de una esfera. Por
ejemplo, en la figura 24, los puntos A y B están a igual distancia de la
fuente. En consecuencia, las densidades de potencia en ellos son
iguales. Esto es valido únicamente cuando se asume un medio físico de
transmisión sin pérdidas. Con base en lo anterior se define la densidad
de potencia en cualquier punto de la esfera como la potencia total
irradiada divida por el área total de la esfera.
La expresión que permite calcular la densidad de potencia irradiada
sobre un punto cualquiera sobre la superficie de un frente de onda
esférico es:
P
PRAD
4 R2
P Densidad de potencia (W/m2)
PRAD Potencia total irradiada (Watts)
R Radio de la esfera
Con base en lo anterior, el campo eléctrico se puede obtener a partir de
la potencia total irradiada, de la siguiente forma:
E
30 * PRAD
R
4.5.2 LEY DEL CUADRADO INVERSO
Cuando se tiene una fuente isotrópica entre más lejos va el frente de
onda respecto a la fuente, la densidad de potencia es más pequeña
debido a las atenuaciones y pérdidas producidas durante el proceso de
propagación en el medio. La potencia total distribuida en la superficie de
la esfera queda igual, sin embargo, como el área de la esfera aumenta
en proporción directa a la distancia de la fuente elevada al cuadrado la
densidad de potencia es inversamente proporcional al cuadrado de la
distancia de la fuente para cualquier punto sobre la superficie de una
esfera exterior la densidad de potencia es:
P2
PRAD
4 R2
2
Y la densidad de potencia en cualquier punto de la esfera interior es:
P1
PRAD
4 R1
2
Por consiguiente:
P2
P1
R1
R2
2
Según lo anterior se puede observar que a medida que se duplica la
distancia a la fuente la densidad de potencia decrece en potencia de
dos; esto es valido cuando se supone el uso de una fuente isotrópica o
simplemente que la velocidad de propagación en todas las direcciones
sea uniforme; un medio de propagación que cumpla con las condiciones
anteriores se le denomina medio isotrópico.
Ejemplo:
Una antena isotrópica irradia una potencia total de 150W. Calcular la
densidad de potencia con respecto a un punto ubicado a 1000 y 2000
metros
Solución
Para el caso de la densidad de potencia a 1000 metros (Punto Interior)
P1
PRAD
4 R1
150
4 (1000) 2
2
11.93 W / m 2
Para el caso de la densidad a 2000 metros (punto exterior)
P2
P1
R1
R2
2
1000
2000
2
0.25
P2
R
P1 1
R2
2
11.93 *10 6 * 0.25
2.98 W / m 2
4.6 ATENUACIÓN Y ABSORCIÓN DE ONDAS
4.6.1 ATENUACIÓN
Aunque en el espacio libre o vacío se considera que no hay pérdida de
energía al propagarse una onda a través de él de acuerdo con la ley de
cuadrado inverso, se pudo analizar que la onda sufre disminuciones en
la densidad de potencia a medida que la onda electromagnética se aleja
de la fuente que lo genero; a esto se le denomina atenuación. Como la
atenuación se debe a la dispersión esférica de la onda a veces se le
denomina atenuación espacial de la onda; esta atenuación se expresa
comúnmente en función del logaritmo de la relación entre densidades de
potencia. Por lo general, se suelen usar los decibelios (símbolo: dB)
como unidad de medida. La expresión matemática para la atenuación
es:
a
10log
Figura 25. Ejemplo de atenuación de una onda de radio
Cuando una onda de radio se estrella con un obstáculo, parte de su
energía se absorbe y se convierte en otro tipo de energía, mientras que
otra parte se atenúa y sigue propagándose. Es posible que otra parte se
refleje. La atenuación se da cuando la energía de una señal se reduce
en el momento de la transmisión. Cuando a es positivo, se denomina
amplificación, y cuando es negativo se denomina atenuación. En los
casos de transmisiones inalámbricas, la atenuación es más común.
La atenuación aumenta cuando sube la frecuencia o se aumenta la
distancia. Asimismo, cuando la señal choca con un obstáculo, el valor de
atenuación depende considerablemente del tipo de material del
obstáculo. Los obstáculos metálicos tienden a reflejar una señal, en
tanto que el agua la absorbe. El debilitamiento de la señal se debe en
gran parte a las propiedades del medio que atraviesa la onda. La tabla
siguiente muestra los niveles de atenuación para diferentes materiales:
Materiales
Grado de
atenuación
Ejemplos
Aire
Ninguno
Aire libre, patio interno
Madera
Bajo
Puerta, piso, medianera
Plástico
Bajo
Medianera
Vidrio
Bajo
Ventanas sin teñir
Vidrio teñido
Medio
Ventanas teñidas
Agua
Medio
Acuario, fuente
Seres vivientes
Medio
Personas, animales y plantas
Ladrillos
Medio
Paredes
Yeso
Medio
Medianeras
Cerámica
Alto
Tejas
Papel
Alto
Bobinas de papel
Concreto
Alto
Muros de carga, pisos, columnas
Vidrio a prueba de balas
Alto
Ventanas a prueba de balas
Metal
Muy alto
Concreto, espejos, armarios y cabinas metálicas
Tabla 3. Niveles de atenuación para diferentes materiales
4.6.2 ABSORCIÓN
La atmósfera terrestre no es un vacío. Más bien está formada por
átomos y moléculas de diversas sustancias gaseosas, líquidas y sólidas.
Algunos
de
esos
materiales
pueden
absorber
las
ondas
electromagnéticas. Cuando una onda electromagnética se propaga a
través de la atmósfera terrestre, se transfiere energía de la onda a los
átomos y moléculas atmosféricos. La absorción de onda por la atmósfera
es análoga a una pérdida de potencia I 2R. Una vez absorbida, la energía
se pierde para siempre, y causa una atenuación en las intensidades de
voltaje y campo magnético, y una reducción correspondiente de
densidad de potencia. La absorción de las radiofrecuencias en una
atmósfera normal depende por lo general de su frecuencia, y es
relativamente insignificante para frecuencias inferiores a 10 GHz. La
figura 26 muestra la absorción atmosférica, en decibeles por kilómetro,
debida al oxígeno y al vapor de agua, para radiofrecuencias mayores de
10 Ghz. Se aprecia que ciertas frecuencias se afectan más o menos por
la absorción, y se producen picos y valles en las curvas. La atenuación
de ondas debida a la absorción no depende de la distancia a la fuente de
radiación, sino más bien a la distancia total que la onda se propaga a
través de la atmósfera. En otras palabras, para un medio homogéneo,
cuyas propiedades son uniformes en todo él, la absorción sufrida
durante el primer kilómetro de propagación es igual que la del último
kilómetro. También, las condiciones atmosféricas anormales, como por
ejemplo lluvias intensas o neblina densa, absorben más energía que una
atmósfera normal. La absorción atmosférica se representa por η y, para
una onda que se propaga de R1 a R2, es (R2 – R1), siendo
el
coeficiente de absorción. Así, la atenuación de onda depende de la
relación R2/R1, y la absorción de onda depende de la distancia entre R1 y
R2. En el caso más real, es decir, en un medio no homogéneo, el
coeficiente de absorción varía mucho de acuerdo con el lugar y origina
difíciles problemas para los ingenieros de sistemas de radio.
Figura 26. Absorción atmosférica de las ondas electromagnéticas
CAPÍTULO 5. PROPIEDADES ÓPTICAS DE LA ONDA DE RADIO
5.1 PROPIEDADES
Cuando una onda electromagnética se propaga en la atmósfera los
frentes de onda y los rayos pueden cambiar su comportamiento con
relación al espacio libre o vacío debido a efectos ópticos tales como:
refracción, reflexión, difracción, e interferencia. A las ondas
electromagnéticas se les puede relacionar con propiedades ópticas,
debido a que las ondas luminosas son ondas electromagnéticas de alta
frecuencia regidas por las ecuaciones de Maxwell.
5.1.1 REFRACCIÓN
Figura 27. Refracción de una onda entre dos medios
La refracción electromagnética es el cambio de dirección de un rayo al
pasar de un medio a otro con distinta velocidad de propagación,
teniendo en cuenta que la velocidad de propagación de una onda
electromagnética es inversamente proporcional a la densidad del medio
en que se propagan el grado de refracción que hay en la interfase entre
dos materiales con diferentes densidades se puede calcular fácilmente
dependiendo de un parámetro conocido como el índice de refracción de
cada material. El índice de refracción para un material se puede calcular
como la relación entre la velocidad de la luz en el espacio vacío y la
velocidad de propagación de la luz a través del medio correspondiente
es:
n
c
v
n Índice de Refracción
c Velocidad de la luz en el espacio libre
v Velocidad de la luz en el material respectivo
La ley que predice el grado de desviación del haz refractado con
relación al haz incidente corresponde a la ley de Snell en la cual
conociendo los índices de refracción de cada material y el ángulo de
incidencia con respecto a la normal dará como respuesta el ángulo con
el cual saldrá el haz refractado con respecto a la normal.
La ley de Snell establece que:
n1 * Sin
n1 , n2
1
n2 * Sin
2
Índices de refracción de los materiales 1 y 2 respectivamente
1
Angulo de Incidencia
2
Angulo de refracción
Otra expresión matemática que relaciona los ángulos de incidencia y
refracción y las constantes dieléctricas de cada material es:
Sin
Sin
1
,
2
1
1
2
2
Constantes dieléctricas de los materiales 1 y 2 respectivamente
Aunque el índice de refracción también es función de la frecuencia en la
mayoría de las aplicaciones la variación del mismo es insignificante por
lo tanto se puede considerar despreciable para su análisis.
5.1.2 REFLEXIÓN
Figura 28. Reflexión de una onda entre dos medios
Cuando una onda electromagnética choca en el limite entre dos medios
de transmisión
diferentes, una parte de la onda es refractada
alcanzando a traspasar el material con el cual se produjo el choque y
parte de la onda es reflejada o regresada sin alcanzar lograr ingresar al
siguiente material; a este fenómeno de reflejar una onda
electromagnética se le denomina reflexión.
Como todas las ondas reflejadas no alcanzan a traspasar el segundo
material mantienen la misma velocidad de propagación que presenta la
onda incidente, como consecuencia de ello, el ángulo con el cual incide
el haz con respecto a la normal será igual al ángulo de reflexión con
respecto a la normal. Sin embargo, la amplitud del campo reflejado es
menor que la amplitud del campo incidente. La relación entre las
intensidades del voltaje reflejado y el voltaje incidente, se le denomina
coeficiente de reflexión, el cual es adimensional y depende no solamente
de las intensidades de voltaje sino también que los ángulos incidente y
reflejado.
La expresión matemática para calcular el coeficiente de reflexión es:
en la que:
= Coeficiente de reflexión (adimensional)
= Intensidad de voltaje reflejado (volts)
= Intensidad de voltaje incidente (volts)
= Angulo reflejado (grados)
= Angulo incidente (grados)
La relación de las densidades de potencia reflejada a incidente es . La
parte de la potencia incidente total que no es reflejada se llama
coeficiente de transmisión de potencia, T, o simplemente el coeficiente
de transmisión. Para un conductor perfecto, T=0. La ley de la
conservación de la energía establece que, para una superficie reflectora
perfecta, la potencia total reflejada debe ser igual a la potencia total
incidente y, en consecuencia,
Para los conductores imperfectos,
como
son funciones del
ángulo de incidencia, la polarización del campo eléctrico y las constantes
dieléctricas de los dos materiales. Si el medio 2 no es conductor
perfecto, algunas de las ondas incidentes penetran en él y se absorben.
Las ondas absorbidas establecen corrientes a través de la resistencia del
material, y la energía se convierte en calor. La fracción de la potencia
que penetra al medio 2 se llama coeficiente de absorción.
Cuando la superficie reflectora no es plana, sino curva, la curvatura
de la onda reflejada es distinta de la onda incidente. Cuando el frente de
la onda incidente es curvo, y la superficie reflectora es plana, la
curvatura del frente de la onda reflejada es igual a la del frente de la
onda incidente.
También se produce reflexión cuando la superficie reflectora es
irregular o áspera; sin embargo, esa superficie puede destruir la forma
del frente de onda. Cuando un frente de onda incidente choca con una,
se dispersa al azar en muchas direcciones. A esa condición se le llama
reflexión difusa, mientras que a la reflexión de una superficie
perfectamente lisa se le denomina reflexión especular o espejo. Las
superficies que se encuentran en un punto intermedio, entre lisas e
irregulares se les denominan superficies semiásperas. Esas superficies
causan una mezcla de reflexión difusa y especular. Una superficie
semiáspera no destruye en su totalidad la forma del frente de onda
reflejado. Sin embargo, hay una reducción de la potencia total. El
criterio de Raleigh establece que una superficie semiáspera refleja como
una superficie lisa siempre y cuando el coseno del ángulo de incidencia
sea mayor que λ/8d, donde d es la profundidad de la irregularidad de la
superficie, y λ es la longitud de la onda incidente.
La ecuación del criterio de Raleigh es:
Figura 29. Reflexión en una superficie semiáspera
5.1.3 DIFRACCIÓN
La difracción consiste en una modulación o redistribución de la energía
dentro de un frente de onda, al pasar cerca de la orilla de un objeto
opaco. La difracción es el fenómeno que permite que las ondas
luminosas o de radio se propaguen en torno a esquinas. Cuando un
frente de onda pasa cerca de un obstáculo o discontinuidad cuyas
dimensiones sean de tamaño comparable a una longitud de onda, no se
puede usar el análisis geométrico simple para explicar los resultados, y
es necesario recurrir al principio de Huygens, que se pude deducir de las
ecuaciones de Maxwell.
El principio de Huygens establece que todo punto sobre
determinado frente de onda esférico se puede considerar como una
fuente puntual secundaria de ondas electromagnéticas, desde la cual se
irradian y se alejan otras ondas secundarias. El principio de Huygens se
ilustra en la figura 30. En la figura 30a, se muestra la propagación
normal de ondas considerando un plano infinito. Cada fuente puntual
secundaria (p1, p2, etc.) irradia energía hacia afuera, en todas las
direcciones. Sin embargo, el frente de onda sigue en su dirección
original, y no se reparte, porque la anulación de ondas secundarias se
hace en todas las direcciones, excepto en la de avance. Por lo anterior,
el frente de onda permanece plano.
Cuando se considera un frente de onda plano y finito, como en la
figura 30b, es incompleta la anulación en direcciones aleatorias. En
consecuencia el frente de onda se reparte hacia afuera, o se dispersa. A
este efecto de dispersión se le llama difracción. La figura 30c, muestra
la difracción en torno a la orilla de un obstáculo. Se ve que la anulación
de ondulaciones sólo es parcial. Se lleva a cabo en torno a la orilla del
obstáculo, lo que permite que las ondas secundarias se “escurran” en
torno a las aristas de un obstáculo, a lo que se llama la zona de sombra.
Este fenómeno se puede observar cuando se abre la puerta de un cuarto
oscuro. Los rayos de luz se difractan en torno a la orilla de la puerta, e
iluminan lo que hay detrás de ella.
Figura 30. Difracción de las ondas electromagnéticas:
(a) principio de Huygens para un frente de onda plano; (b) frente de una onda
finita a través de una abertura; (c) frente de onda rodeando una arista
5.1.4 INTERFERENCIA
La interferencia consiste en el acto de oponerse o como su nombre lo
indica interferir con la forma normal de una onda; esta se produce
siempre que se combinen dos o más ondas electromagnéticas
provocando con ello alteraciones en la forma original de la señal,
degradando el óptimo funcionamiento del sistema. Los fenómenos de
refracción, reflexión y difracción son fenómenos propios de la óptica
geométrica, fundamentados principalmente en el comportamiento de
rayos y frentes de onda.
Sin embargo, la interferencia obedece al principio de la superposición
lineal de las ondas electromagnéticas el cual se presenta cuando dos o
más ondas ocupan el mismo punto del espacio en forma simultánea.
Este principio explica que la intensidad total de voltaje en un punto dado
en el espacio, corresponde a la sumatoria vectorial de cada una de las
señales incidentes.
La figura 31 muestra la interferencia entre dos ondas electromagnéticas
en el espacio libre. En el punto X las dos ondas ocupan el mismo lugar
en el espacio. Sin embargo la onda B ha recorrido una trayectoria
diferente a la de la onda A y, en consecuencia, sus ángulos de fase
relativos pueden ser distintos. Si la diferencia de distancias recorridas es
un múltiplo entero impar de la mitad de la longitud de onda, se presenta
la anulación total. Si la diferencia es un múltiplo entero par de la mitad
de la longitud de onda, tiene lugar un reforzamiento. Lo más probable
es que la diferencia de distancias sea intermedia entre las dos, y se
produce una anulación o reforzamiento parcial. Para frecuencias
menores que VHF, las longitudes de onda relativamente grandes evitan
que la interferencia sea un problema apreciable. Sin embargo, con UHF
o más, la interferencia ondulatoria puede ser grave.
Figura 31. Interferencia de las ondas electromagnéticas
5.2 PROPAGACIÓN TERRESTRE DE LAS ONDAS ELECTROMAGNÉTICAS
Toda aquella onda electromagnética que se propague dentro de la
atmósfera terrestre se le denomina onda terrestre y el proceso de
comunicación entre dos o más puntos de la tierra se conoce como radio
comunicación terrestre. Toda onda electromagnética terrestre
es
afectada por las condiciones atmosféricas y con ello se puede decir que
dependen de la clase de sistema y del ambiente propagándose en
diferentes formas viajando en línea recta o alterando su trayectoria.
Figura 32. Modos de propagación de ondas electromagnéticas
Existen tres formas de propagación de las ondas electromagnéticas en la
atmósfera terrestre: onda terrestre, onda espacial (compuesta por
ondas directas y ondas reflejadas en el suelo) y ondas celestes o
ionosféricas. Una de las características más importantes de las ondas
terrestres es que a frecuencias inferiores de 1.5MHz, las ondas
presentan mayor difusión y menor perdida en el momento de su
propagación las ondas celestes son utilizadas para aplicaciones de alta
frecuencia y las ondas espaciales se utilizan para aplicaciones de muy
alta frecuencia.
5.2.1 PROPAGACIÓN DE ONDAS TERRESTRES
Se denomina onda terrestre a toda aquella onda electromagnética que
viaje por la superficie de la tierra denominadas también ondas
superficiales. Una característica de las ondas terrestres es que deben
estar polarizadas verticalmente, ya que si el campo eléctrico de este tipo
de ondas se polariza horizontalmente quedaría en paralelo de la
superficie de la tierra generando un corto circuito debido a la
conductividad del suelo.
El campo eléctrico generado por una onda terrestre induce voltajes
provocando la circulación de corrientes semejantes a las de una línea de
transmisión. Como toda onda sufre pérdidas o atenuaciones a medida
que se propagan debido a la resistencia ofrecida por el ambiente y por el
medio de transmisión; a mayor frecuencia de este tipo de ondas mayor
es la cantidad de perdidas en la onda electromagnética. El uso de ondas
terrestres es común en aplicaciones de comunicación marítima y de
radio navegación.
Dentro de las ventajas del uso de ondas terrestres en el momento de
propagarse se pueden considerar:
Las ondas terrestres son poco afectadas por las condiciones
variables de la atmósfera
Se pueden realizar procesos de comunicación entre dos lugares
cualesquiera del mundo siempre y cuando se utilice la potencia
suficiente de transmisión
Las desventajas de la propagación de ondas terrestres son las
siguientes:
Las pérdidas en el terreno varían mucho de acuerdo con el
material superficial y su composición
Se limitan a frecuencias muy bajas, bajas e intermedias (VLF,LF y
MF) y requieren grandes antenas
Requieren una potencia de transmisión relativamente alta
5.2.2 PROPAGACIÓN DE ONDAS ESPACIALES
Las ondas espaciales son todas aquellas ondas que incluyen las ondas
directas, que son aquellas que viajan en línea recta o a línea de vista
entre las antenas trasmisoras y receptoras, las cuales pueden ser
irradiadas por varios kilómetros. La única restricción para este tipo de
propagación, es que esta limitada por la curvatura de la tierra.
Otro tipo de ondas espaciales son las ondas reflejadas en el suelo las
cuales se forman cuando son reflejadas por la superficie terrestre en el
momento de la propagación de la onda electromagnética entre antenas
transmisoras y receptoras.
Figura 33. Propagación de Ondas Espaciales
La curvatura de la tierra tal como se menciona es un obstáculo para la
propagación de ondas espaciales, esta curvatura, presenta un horizonte
de propagación dentro del cual se pueden realizar procesos de
comunicación a línea de vista denominado horizonte de radio.
Debido a la refracción atmosférica el horizonte de radio esta más allá del
horizonte óptico para la atmósfera estándar común. Un cálculo común
para determinar la longitud del horizonte de radio es que es equivalente
4/3 del horizonte óptico. Dentro de los métodos comunes para aumentar
el tamaño del horizonte de radio consiste en elevar las antenas de
transmisión o recepción lo más alto posible ubicándolas en torres, sitios
montañosos o edificios altos.
Una forma para calcular el horizonte de radio en función de la altura de
la antena es:
d
2 *h
d Distancia al horizonte de radio
h Altura de la antena
Y la distancia máxima entre antena transmisora y receptora es:
d
d
2 * hT
dT
dR
2 * hR
2 * ( hT
hR )
d Distancia total
hT Altura de la antena Transmisora
hR Altura de la antena Receptora
d T Distancia de radio a la antena transmisora
dR
Distancia de radio a la antena receptora
La distancia máxima entre un transmisor y receptor sobre un terreno
promedio se puede calcular por:
d MAX
17 hT
17 hR
17 * (hT
hR )
Figura 34. Ondas Espaciales y horizonte de Radio
5.2.3 PROPAGACIÓN POR ONDAS CELESTES
Las ondas electromagnéticas celestes son aquellas que se propagan con
polarización horizontal; en aplicaciones comunes, este tipo de ondas se
irradia en una dirección que forma un ángulo relativamente grande con
la tierra.
Son ondas que se irradian directamente hacía el cielo en donde son
reflejadas o refractadas hacía la superficie terrestre por la ionosfera, por
esta razón se le denomina propagación ionosférica. La ionosfera, es la
región del espacio que está entre 50 y 400 kilómetros sobre la superficie
terrestre; esta capa de la tierra es la encargada de absorber grandes
cantidades de energía solar ionizando moléculas de aire formando con
ello electrones libres.
Cuando una onda electromagnética atraviesa la ionosfera el campo
eléctrico de la onda ejerce una fuerza sobre los electrones libres
colocándolos en un estado vibrante provocando con ello la refracción de
la onda electromagnética de nuevo hacia la superficie terrestre, la
densidad de la ionosfera esta condicionada por el medio ambiente y la
temperatura.
Existen tres capas que componen la ionosfera la capa: d, e y f.
Figura 35. Capas Ionosféricas
5.2.3.1 CAPA D
Es la capa inferior de la ionosfera, se encuentra ubicada entre los 50 y
100 km sobre la superficie terrestre; por ser la más retirada al sol
presenta poca ionización y con ello tiene muy poco efecto sobre la
dirección de propagación de las ondas de radio. Esta capa refleja las
ondas de VLF y LF, y absorbe las ondas MF y HF.
5.2.3.2 CAPA E
Ubicada en la zona intermedia de la ionosfera entre los 100 y los
140Km. sobre la superficie terrestre, esta capa al igual que la capa D
desaparecen casi totalmente en horas de la noche alcanzando su
máxima densidad en horas en donde la energía solar presenta su mayor
incidencia sobre la tierra, esta capa favorece la propagación de ondas
superficiales como MF y refleja algo de ondas HF durante el día.
5.2.3.3 CAPA F
Es la capa superior de la ionosfera se encuentra subdividida en dos
capas F1 y F2, como la densidad de la ionosfera depende de la
temperatura, esta capa F presenta dos comportamientos: durante el día,
la capa F1 está entre los 140 y 250 Km sobre la superficie terrestre. La
capa F2 entre los 140 y 300 Km sobre la superficie terrestre durante el
invierno, y de 250 a 350 Km en el verano. Durante la noche, las capas
F1 y F2 se combinan y forman una sola capa. La capa F1 es la encargada
de absorber y atenuar algunas ondas de tipo HF, aunque la mayoría de
las ondas atraviesan la capa F2, donde son reflejadas hacia la tierra.
Figura 36. Comportamiento de las capas ionosféricas a
diferentes horas del día y algunos meses del año
CAPÍTULO 6. TÉRMINOS Y DEFINICIONES DE PROPAGACIÓN
6.1 FRECUENCIA CRÍTICA Y ANGULO CRÍTICO
La frecuencia crítica (FC), se define como la máxima frecuencia que se
debe propagar como ondas celestes y es reflejada por la ionosfera
nuevamente hacia la superficie terrestre. Esta frecuencia depende de la
densidad de ionización, la cual es susceptible de modificación acorde con
las condiciones atmosféricas y de radiación solar. Debido a éste
parámetro y con el fin de permitir la reflexión de las ondas celestes por
parte de las ionosferas, se acostumbra disminuir el ángulo vertical de
radiación debido a que al hacer esto se puede recorrer una distancia
mayor en la ionosfera y mayor probabilidad de ser reflejada nuevamente
hacia la superficie. Con base en lo anterior cada frecuencia tiene un
ángulo vertical máximo con el cual se puede propagar y reflejar por la
ionosfera a este ángulo se le denomina ángulo crítico.
Figura 37. Angulo Crítico
La técnica que permite cuantificar el ángulo critico se denomina sondeo
ionosférico, el cual consiste en propagar una señal directamente hacia
arriba, ir aumentando gradualmente la frecuencia de la señal irradiada
y a medida que se va aumentando la frecuencia las ondas son enviadas
y reflejadas nuevamente a la superficie hasta que llega un momento en
el cual la frecuencia no alcanza a ser reflejada por la ionosfera
propagándose directamente al espacio exterior; esa frecuencia con la
cual no fue posible su refracción es la que se conoce como frecuencia
crítica.
6.2 ALTURA VIRTUAL
Es aquella altura sobre la superficie terrestre desde la cual parece
reflejarse una onda esta altura virtual en la mayoría de los casos es
mayor que la altura real alcanzada por la onda en el momento de ser
refractada.
Figura 38. Altura Virtual
6.3 MÁXIMA FRECUENCIA ÚTIL
La máxima frecuencia útil (MUF), es la mayor frecuencia que se puede
utilizar para propagación de ondas celestes entre dos puntos de la
superficie terrestre la MUF se puede calcular de la siguiente forma:
La MUF es un parámetro útil para ser cálculos de frecuencias en
procesos de propagación de ondas celestes, sin embargo, debido a la
inestabilidad de la ionosfera a causa de las condiciones climáticas y de
radiación solar se recomienda trabajar con el 85 % del valor de la MUF
obteniéndose comunicaciones más confiables. A esta frecuencia se le
denomina frecuencia optima de trabajo (OWF), (optimun working
frequency).
6.4 DISTANCIA DE SALTO
Es la distancia mínima desde una antena de transmisión a la que
regresara a la tierra una onda celeste de determinada frecuencia:
Figura 39. Distancia de Salto
6.5 PÉRDIDAS EN TRAYECTORIA POR EL ESPACIO LIBRE
Las pérdidas en trayectoria por el espacio libre se definen como aquellas
pérdidas de una onda electromagnética que al propagarse en línea recta
por el vacío no corresponden a pérdidas producidas por absorción
reflexión u otros factores.
La expresión matemática que describe las perdidas en trayectoria por el
espacio libre es:
LP
4 D
2
4 *D* f
c
2
LP
Perdidas en trayectoria por el espacio libre (Adimensional)
D Distancia recorrida (Km)
Calculando su expresión equivalente en dB.
Cuando la frecuencia se expresa en MHz
LP (dB)
32 .4 20 log( f MHZ ) 20 log( DKm )
Cuando la frecuencia se expresa en GHz
LP (dB)
92 .4 20 log( f MHZ ) 20 log( DKm )
6.6 MARGEN DE DESVANECIMIENTO
Las pérdidas originadas en una onda electromagnética producidas por
perturbaciones meteorológicas, reflexión, refracción, se les denominan
desvanecimiento. Estas pérdidas se pueden presentar en ciertos lapsos
de tiempo con mayor o menor intensidad.
El margen de desvanecimiento, es una pequeña tolerancia que se
agrega a las perdidas normales en la trayectoria de una onda
electromagnética, dentro de las cuales se tienen en cuenta aquellas
pérdidas provocadas por factores impredecibles como por ejemplo:
atenuaciones por múltiples trayectorias, topografía del terreno,
condiciones atmosféricas temporales entre otras.
6.7 EJERCICIOS PROPUESTOS
PROPAGACION Y ONDAS ELECTROMAGNÉTICAS
1. Calcular la densidad de potencia de una antena isotrópica en donde la
potencia irradiada es 1000 vatios y la distancia de la antena es 20 kms
describa los efectos sobre la densidad de potencia si se triplica la distancia
a la antena de transmisión
2. calcular el horizonte de radio para una antena transmisora de 100 m de alto
y una antena receptora de 50m
3. Calcular la máxima frecuencia útil para una frecuencia crítica de 15 Mhz y
un ángulo de incidencia de 45º
4. Si la densidad de potencia en un punto es de 0.005 µW y en otro punto es
0.00005 µW calcular la atenuación en Db
5. Calcular la distancia máxima entre antenas de igual altura en donde la
altura de la antena es de 40 pies
6. Calcular el horizonte de radio para dos antenas transmisora y receptora de
200 m y 150 m respectivamente
7. Calcular la pérdida en trayectoria para las siguientes frecuencias y
distancias:
8. Calcular el ángulo de refracción para una relación de dieléctrico de 0.4 y un
ángulo de incidencia de 18 grados
6.8 PREGUNTAS
1.
2.
3.
4.
Describa un rayo electromagnético y un frente de onda
Qué es densidad de potencia e intensidad de voltaje
Explique la ley del cuadrado inverso
Defina los siguientes conceptos: atenuación, absorción, reflexión,
refracción, difracción
5. Cuales son las ventajas y desventajas de la propagación de ondas
terrestres, ondas espaciales y ondas celestes
6. Cuales son las capas que conforman la ionosfera, explique cada una de
ellas
7. Qué es máxima frecuencia útil
UNIDAD No. 3
ANTENAS Y GUÍAS DE ONDA
OBJETIVOS DE LA UNIDAD
Esta unidad facilita que el estudiante adquiera lo conceptos básicos y
comprenda las leyes que rigen el funcionamiento de las antenas y guías
de onda y su importancia en el campo de la propagación de información.
El estudiante al finalizar la unidad estará en capacidad de comprender y
calcular los principales parámetros que rigen el funcionamiento de las
antenas tales como: densidad de potencia, ganancia, potencia de
entrada, impedancia característica, pérdidas de propagación, entre otros
elementos indispensables para su óptimo funcionamiento.
La unidad Incentiva al estudiante a realizar procesos de investigación y
profundización en temas relacionados con los diferentes tipos de
antenas existentes, su aplicación, formas de diseño, cálculos de sus
principales parámetros y su importancia en el dinámico campo de las
telecomunicaciones.
CAPÍTULO 7. CONCEPTOS BÁSICOS DE ANTENAS
7.1 INTRODUCCIÓN A LAS ANTENAS
Una antena es un dispositivo constituido por un conductor metálico
capaz de radiar y capturar ondas electromagnéticas se utiliza
convencionalmente para acoplar líneas de transmisión con el espacio
libre, acoplando la energía de un transmisor y un receptor a la
atmósfera terrestre. Una antena es capaz de convertir energía eléctrica
en ondas electromagnéticas y viceversa. Una guía de onda es una línea
de transmisión especial utilizada para interconectar una antena con un
transceptor facilitando con ello el trabajo con ondas electromagnéticas.
Las Antenas están consideradas como uno de los elementos más
importantes
requerido en un proceso de comunicación inalámbrico;
estos dispositivos están específicamente diseñados para radiar o recibir
ondas electromagnéticas, adaptando en todo momento ondas guiadas,
las cuales se transmiten a través de conductores o guías, facilitando con
ello su propagación en el espacio libre.
Una definición mucho más técnica, establecida por el Institute of
Electrical and Electronics Engineers (IEEE), define una antena como
aquella parte de un sistema transmisor o receptor diseñada
específicamente para radiar o recibir ondas electromagnéticas (IEEE Std.
145-1983).
La misión de la antena es irradiar la potencia que se le suministra con
las características de direccionalidad adecuadas según su aplicación. Por
ejemplo, en radiodifusión o comunicaciones móviles se acostumbra el
uso de antenas que permitan irradiar una zona en forma
omnidireccional, caso contrario a las aplicaciones orientadas a las
radiocomunicaciones fijas en donde se busca que la radiación sea
enfocada hacia un solo sentido, es decir, requieren el uso de antenas
direccionales.
Las antenas pueden ser de diferentes tipos, esto varía según la
aplicación que se requiera y los parámetros de configuración y de
sintonía propios del sistema de transmisión o recepción, en donde el fin
principal es el de poder concentrar una cantidad de energía, lograr
irradiarla y poder en algún instante detectar ésta energía en un punto
distante y convertirla nuevamente en su forma original para realizar una
tarea específica.
Se puede decir que las funciones básicas de una antena son dos:
transmitir y recibir, definiendo cada aplicación condiciones particulares
sobre la direccionalidad de la antena, niveles de potencia que debe
soportar, frecuencia de trabajo y otros parámetros que serán expuestos
posteriormente.
Una onda presenta dos características principales: frecuencia (f) y
longitud de onda (λ), ambas se encuentran relacionadas por la
expresión que define la velocidad de propagación en el medio, en el
caso particular, las ondas electromagnéticas pueden viajar a la velocidad
de la luz (c=3*108 m/s=λf) considerándose la velocidad de propagación
de una onda en el vacío.
Debido a la gran cantidad de ondas electromagnéticas que viajan a
través del espacio constantemente, cada una de ellas con características
propias según la aplicación que las requiera, se ha visto la necesidad de
clasificar éstas ondas según rangos de frecuencias estableciéndose con
ello divisiones acordes con cada aplicación según sea el caso definidas
por organismos de normalización o estandarización
A continuación se ilustran unos cuadros que muestran claramente éstas
divisiones del espectro electromagnético y sus principales características
según sea requerido.
Tabla 4. Denominación de las bandas de frecuencias por décadas
En el caso de las frecuencias propias de las aplicaciones orientadas hacia
el uso de microondas existe una subdivisión la cual es ampliamente
utilizada en la actualidad.
Tabla 5. Denominación habitual de las bandas de frecuencias en
microondas
En el caso de las frecuencias superiores tales como ondas
electromagnéticas correspondientes al infrarrojo, visible, ultravioleta y
rayos X.
Tabla 6. Denominación de las bandas a frecuencias superiores
Según la aplicación que requiera el uso de antenas, es necesario tener
claro el valor de la frecuencia de la señal a irradiar; las antenas tienen
unas características de impedancia y de radiación las cuales dependen
directamente del valor de la frecuencia a utilizar. El análisis de dichas
características se realiza a partir de las ecuaciones de Maxwell en el
dominio de la frecuencia, utilizando las expresiones de los campos en
forma compleja o fasorial. Cada aplicación y cada banda de frecuencias
presentan características peculiares que dan origen a una gran variedad
de formas y tipos de antenas.
7.2 FUNCIONAMIENTO BÁSICO DE UNA ANTENA
En los sistemas de radiocomunicación los transmisores y los receptores
están conectados a través de una línea de comunicación acoplándose al
espacio libre a través de antenas. Una antena es un dispositivo pasivo el
cual no puede amplificar una señal, es considerado un dispositivo
reciproco porque las características y el desempeño de transmisión y
recepción son idénticas tales como: ganancia, directividad, frecuencia de
operación, resistencia de radiación, ancho de banda, eficiencia entre
otros parámetros.
Una antena permite acoplar un sistema de radio comunicación en forma
semejante a un transformador en donde son acopladas las ondas
electromagnéticas propagadas por el espacio libre con el sistema
electrónico. Un sistema de acoplamiento con una antena se puede
representar con una red de cuatro terminales, en donde, la energía
electromagnética debe ser transferida desde la antena trasmisora hacia
el espacio libre y una segunda etapa, donde la energía es tomada del
espacio libre hacia una antena receptora.
Las antenas de transmisión deben ser capaces de manipular potencias
grandes por lo cual exige su construcción con materiales resistentes, sin
embargo, para el caso de las antenas de recepción basta con alambres
de diámetros pequeños debido a que los voltajes y corrientes que se
circular a través de ellos son muy pequeños.
Existen casos en donde se utiliza la misma antena para enviar y recibir
señales, hay que tener en cuenta que las potencias utilizadas para
transmisión son elevadas y las potencias de recepción son bajas en cuyo
caso es necesario incorporar un sistema de aislamiento para transmisión
y recepción con la misma antena evitando que grandes cantidades de
potencia puedan alcanzar el circuito receptor el cual es bastante sensible
en cuyo caso es recomendado utilizar un elemento especial para tal fin
conocido como diplexor.
7.3 ASPECTOS FUNDAMENTALES DE LAS ANTENAS
La antena debe transferir la máxima cantidad de energía desde el cable
o guíaonda procedente del transmisor hacia la dirección donde se
encontrará la estación receptora correspondiente. Para ello, la
impedancia característica de la antena debe acoplarse a la impedancia
del cable o guíaonda a la cual está conectada.
Los cables coaxiales se producen con impedancias de 50 o 75 Ω. En
televisión se utiliza frecuentemente el valor de 75 Ω, pero en todas las
demás aplicaciones el valor predominante es de 50 Ω y es el que
utilizaremos en esta unidad. Cuando la impedancia de la antena es
diferente a la de la guíaonda o cable que la alimenta, parte de la energía
entregada a la antena se reflejará hacia el alimentador donde puede
inclusive causar daños en el transmisor. En todo caso disminuye la
cantidad de energía disponible para la comunicación, por lo que es
necesario siempre esmerarse para lograr que la impedancia del
alimentador se acople a la de la antena. Las pérdidas por
desacoplamiento de impedancia son fácilmente calculables. Un aspecto
fundamental de las antenas es el principio de reciprocidad, que
establece que el comportamiento de la antena en transmisión es
idéntico al comportamiento de la antena en recepción. Esto permite
enfocar nuestras ideas hacia la transmisión o recepción, según sea más
fácil, y luego extender el concepto hacia el comportamiento recíproco.
Así, una antena que transmita máxima señal en una dirección dada,
también recibirá máxima señal en esa misma dirección.
7.4 CARACTERÍSTICAS ESENCIALES DE LAS ANTENAS
Entre las principales características de las antenas podemos encontrar:
• Ganancia de la antena
• Diagrama de radiación o patrón de radiación
• Ancho del haz
• Impedancia de entrada
• Polarización
• Otras características, entre las cuales se encuentra el cociente entre la
ganancia del lóbulo principal y el lóbulo trasero o “ Front to back ratio”,
la Pérdida de retorno y el Ancho de banda.
7.4.1 GANANCIA DE ANTENA
Para comprender la idea de ganancia de las antenas primero debemos
entender un concepto básico:
Antena Isotrópica: Es la que irradia (o recibe) desde todas las
direcciones con la misma intensidad. Aunque es físicamente irrealizable,
el concepto de antena isotrópica se utiliza como modelo de comparación
con las antenas reales. Como irradia con igual eficacia en todas
direcciones, decimos que su diagrama o patrón de radiación es una
esfera. Un ejemplo de lo que se aproxima a una antena isotrópica es la
luz producida por un bombillo, que se proyecta en todas direcciones con
la misma intensidad, excepto en la base del bombillo.
Definimos a la ganancia de una antena dada como el cociente entre la
cantidad de energía irradiada en la dirección preferencial y la que
irradiaría una antena isotrópica alimentada por el mismo transmisor.
Este número lo expresamos en decibelios con relación a la isotrópica y
por ende se denota en dBi.
Las antenas inalámbricas no son diseñadas para difundir la energía en
todas direcciones en cambio se diseñan para dirigir la señal total de
radio en el área a la cual aspiramos a proveer de cobertura.
La ganancia de antena es una manera de medir cuán directiva es una
antena, en comparación con una antena isotrópica. Entre más grande
sea la ganancia de una antena, esta es más directiva y el haz de radio
és más angosto.
Es muy importante entender que las antenas son elementos pasivos que
no amplifican la señal de radio. Las antenas sólo concentran la señal en
la cierta dirección. Cuando se usa como transmisora la antena es
responsable de dirigir la potencia del radiotransmisor en la cierta
dirección; cuando actúa como receptora la antena colecta la potencia de
radio que le envió el receptor.
Aunque las antenas son elementos pasivos y no proveen ninguna
amplificación, desde el punto de vista de nuestros cálculos en el
presupuesto del enlace de radio, son consideradas como una "Ganancia"
de la señal de radio.
Si una antena tiene un ganancia de 3 dBi en cierta dirección, quiere
decir que la potencia transmitida o recibida en esa dirección es
equivalente a la potencia que será transmitida o recibida por una antena
isotrópica que usa doble de la potencia en el radiotransmisor.
La ganancia de una antena es el producto de la directividad
(determinada exclusivamente por factores geométricos) y la eficiencia
de la antena, que depende del material de la que está construida y
de las imperfecciones de manufactura. La eficiencia de la antena se
suele expresar con la letra griega eta [η] y varía normalmente entre
40% y 60%.
Algunas veces la ganancia de las antenas es expresada en dBd. En tal
caso la antena de referencia es una antena de dipolo (dipole). Una
antena dipolo tiene un ganancia de 2.14 dBi comparado con una antena
isotrópica. Por ello, si la ganancia de una antena dada se expresa en
dBd resultará en un valor inferior en 2,14 dB respecto a la ganancia de
la misma antena expresada en dBi.
Ganancia en dBd = Ganancia en dBi - 2,1
7.4.2 DIAGRAMA DE RADIACIÓN
El diagrama de radiación o patrón de radiación es una gráfica de la
potencia de la señal trasmitida en función del ángulo espacial, en ellos
podemos apreciar la ubicación de los lóbulos laterales y traseros, los
puntos en los cuales no se irradia potencia (NULOS) y adicionalmente
los puntos de media potencia.
Los diseñadores de antenas se esmeran por reducir al mínimo los
lóbulos secundarios, laterales y traseros ya que generalmente son
perjudiciales, esto se logra mediante la modificación de la geometría de
la antena. Desde el punto de vista formal, el campo electromagnético
producido por una antena a gran distancia corresponde a la
transformada de Fourier en dos dimensiones de la distribución de cargas
eléctricas en la antena.
Figura 40. Diagrama de radiación
Los diagramas de radiación son volúmenes y como tal se representan en
forma tridimensional, en la siguiente figura podemos ver dos diagramas
de radiación, en la misma observamos que se ha representado la
intensidad mínima por el color rojo y la máxima con el color azul.
a) Un Dipolo
b) Antena de bocina (horn) estándar
Figura 41. Diagrama de radiación Tridimensional
Normalmente los diagramas de radiación se representan de forma bidimensional en dos planos, el vertical y el horizontal, estos planos son
presentados en coordenadas rectangulares o en coordenadas polares
como se muestra a continuación
Figura 42. Representación de un diagrama de radiación en
coordenadas polares
Figura 43. Representación de un diagrama de radiación de una
antena Yagi en coordenadas rectangulares
7.4.3 ANCHO DEL HAZ (beamwidth)
El ancho del haz (beamwidth) es el ángulo subtendido por la radiación
emitida entre los puntos en que la potencia disminuye a la mitad, (3 dB)
respecto a la radiación máxima.
Figura 44. Puntos de media potencia en un diagrama de radiación
Usando el diagrama de radiación en la figura 44, podemos determinar la
cobertura espacial donde la antena ofrece buena cobertura. El ángulo
entre los puntos de media potencia es conocido como ancho del haz o
“beamwidth” en inglés y se define tanto para el plano horizontal como
para el plano vertical. Sólo en el caso de una antena con simetría
circular perfecta ambos ángulos son iguales. Existe una relación inversa
entre la ganancia y la extensión de la cobertura: una antena de alta
ganancia tendrá una anchura de haz muy pequeña.
7.4.4 IMPEDANCIA DE ENTRADA
Es el cociente entre el voltaje aplicado a los terminales de entrada y la
corriente resultante. En general tiene una parte resistiva y otra parte
reactiva. Para máxima transferencia de potencia la impedancia de la
antena debe estar acoplada a la de la línea de transmisión que la
alimenta. La calidad del acoplamiento se mide en términos de la relación
de onda estacionaria, VSWR (Voltage Standing Wave Ratio).
Idealmente debería ser la unidad, cuando las impedancias son
exactamente iguales. Cuando excede de 2 empieza a haber problemas,
Si es mayor que 3 el transmisor sufre peligro e implica desperdicio de
mucha potencia.
Figura 45. Transferencia de potencia desde una fuente a la
carga. En nuestro caso la fuente es el transmisor y la carga la
antena.
Cuando una antena es conectada a un transmisor, lo que se busca es
lograr radiar el máximo de potencia posible con un mínimo de pérdidas
en ella. Para lograrlo, la antena y el transmisor deben acoplarse de tal
forma que permita realizar una máxima transferencia de potencia.
Para medir la potencia radiada por una antena es importante conocer su
impedancia, la cual es medida a la entrada de la antena y es definida
como impedancia de entrada ( Z EN ) mediante relaciones tensióncorriente en ese punto.
La impedancia de una antena se define como la relación entre la tensión
y la corriente en sus terminales de entrada. Dicha impedancia es en
general compleja, con lo cual presentará una componente real (R) o
Resistiva y una componente imaginaria (X) o Reactiva, en donde ambas
dependen de la frecuencia.
El punto de la antena donde se conecta la línea de transmisión se
denomina Terminal de entrada de la entrada o simplemente punto de
alimentación
Z EN
V EN
I EN
La impedancia de entrada es un parámetro de gran trascendencia,
debido a que es la encargada de regir las tensiones que se deben aplicar
para obtener determinados valores de corriente en la antena y, en
consecuencia, una determinada potencia radiada. Si la parte reactiva es
grande, hay que aplicar tensiones elevadas para obtener corrientes
apreciables; si la resistencia de radiación es baja, se requieren elevadas
corrientes para tener una potencia radiada importante.
La impedancia que ve el transmisor debe ser igual a su impedancia de
salida, de otra manera se produce una onda reflejada que no sólo
disminuye la señal efectivamente irradiada, sino que puede llegar a
dañar al transmisor si es muy elevada.
7.4.5 POLARIZACIÓN DE LA ANTENA
Una onda electromagnética está formada por campos eléctricos y
magnéticos íntimamente ligados que se propagan en el espacio. La
dirección del campo eléctrico se corresponde con la polarización de esta
onda. La polarización de una antena corresponde a la dirección del
campo eléctrico emitido por una antena. Esta polarización puede ser:
Vertical, Horizontal y Elíptica, Circular (Hacia la derecha o hacia la
izquierda).
Cuando se habla de polarización de una antena, se hace referencia a la
orientación del campo eléctrico que se irradia de ella. Las antenas
pueden polarizarse linealmente (Polarización horizontal y vertical),
elípticamente o circularmente. Cabe recordar que, una onda
electromagnética contiene un campo eléctrico y uno magnético
perpendiculares entre si. La polarización de una onda electromagnética
plana no es mas que la orientación del vector de campo eléctrico con
respecto a la superficie de la tierra es decir respecto al horizonte si la
polarización permanece constante se denomina polarización lineal, la
polarización lineal; si el campo eléctrico se propaga en dirección paralela
a la superficie de la tierra se dice que la onda esta polarizada
horizontalmente por otra parte si el campo eléctrico se propaga
perpendicularmente a la superficie terrestre se dice que la onda esta
polarizada verticalmente.
Si el vector de polarización gira 360º a medida que la onda recorre una
longitud de onda por el espacio y la intensidad de campo eléctrico es
igual en todos los ángulos de polarización se dice que la onda tiene
polarización circular sin embargo cuando la intensidad de campo
eléctrico varia con cambios en la polarización se dice que es una
polarización elíptica.
7.4.5.1 POLARIZACIÓN VERTICAL
Si el campo eléctrico permanece en la dirección vertical durante toda la
trayectoria de una onda decimos que tiene polarización vertical, para un
dipolo el movimiento de los electrones dentro del alambre responde al
campo eléctrico y por lo tanto define la polarización.
Figura 46. Polarización Vertical
7.4.5.2 POLARIZACIÓN HORIZONTAL
Si colocamos el alambre horizontalmente, tendremos polarización
horizontal.
Figura 47. Polarización Horizontal
7.4.5.3 POLARIZACIÓN ELÍPTICA
La polarización elíptica se produce cuando el campo eléctrico va girando
en el plano perpendicular a la dirección de propagación, como un
sacacorchos. Tiene ciertas ventajas en transmisión satelital y es la
polarización producida por antenas helicoidales.
Un caso particular de la polarización elíptica es la polarización circular la
cual puede ser hacia la derecha o hacia la izquierda.
En general, se puede emplear cualquier tipo de polarización, lo
importante es que ambos extremos de un enlace utilicen el mismo tipo
de polarización. En polarización elíptica deben tener el mismo sentido
de giro.
7.4.5.4 POLARIZACIÓN CRUZADA
No importa la polarización que se escoja, todas las antenas deben tener
la misma polarización si pertenecen a la misma red de RF. La
polarización cruzada tiene lugar cuando un extremo del enlace tiene
polarización diferente del otro extremo. La polarización cruzada implica
una pérdida de señal que puede alcanzar 20 decibeles.
Esto se puede aprovechar para que dos señales a la misma frecuencia
compartan un mismo espacio geográfico, diferenciándose en la
polarización.
7.4.6 OTRAS CARACTERÍSTICAS DE LAS ANTENAS
7.4.6.1 COCIENTE ENTRE LA GANANCIA DEL LÓBULO PRINCIPAL
Y EL LÓBULO TRASERO
El “front to back ratio”, o cociente entre la ganancia del lóbulo principal
y el lóbulo trasero. Generalmente es expresado en dB. Es relevante
cuando se utilizan repetidores para aumentar el alcance de un enlace,
donde se quiere minimizar la potencia irradiada hacia atrás.
7.4.6.2 PÉRDIDA DE RETORNO
La pérdida de retorno es una forma de expresar la desadaptación de
impedancias. Es una medida logarítmica expresada en dB, que compara
la potencia reflejada por la antena con la potencia entregada por el
transmisor.
Siempre existe cierta cantidad de energía que va a ser reflejada hacia el
transmisor, pero una pérdida de retorno elevada implica un
funcionamiento inadecuado de la antena.
7.4.6.3 ANCHO DE BANDA
El ancho de banda consiste en el rango de frecuencias dentro del cual la
antena funciona satisfactoriamente. Para calcular el ancho de banda es
necesario identificar la diferencia entre las frecuencias de media
potencia y se acostumbra expresar en términos de porcentaje.
La expresión es la siguiente:
BW
f2
f1
f
* 100
f Frecuencia de operación óptima
f1 , f 2 Frecuencias de mitad de potencia o -3dB
BW Ancho de Banda
7.5 SISTEMAS COORDENADOS O REFERENCIALES
Un tema de gran importancia en el área de la propagación
electromagnética es el sistema de coordenadas a utilizar. La posición de
eventos en el espacio se define respecto de un punto fijo llamado origen
de coordenadas. La definición de un origen de coordenadas y un origen
de tiempos crea un sistema de referencia o referencial. El vector
posición es el vector que se dirige desde el origen de coordenadas hasta
la posición a definir. La posición de un punto en el espacio respecto a un
origen de coordenadas se determina mediante él vector posición.
Para operar en un sistema de referencia es útil definir coordenadas, que
son variables escalares que permiten expresar los campos escalares y
vectoriales así como los elementos de arco, superficie y volumen que
aparecen en las ecuaciones integrales.
Para elegir un sistema adecuado de coordenadas es necesario definir la
simetría del problema físico en cuestión. De los múltiples sistemas de
coordenadas que se pueden definir, la práctica ha privilegiado aquellos
sistemas llamados de coordenadas separables. Estos son sistemas que
permiten pasar de ecuaciones diferenciales a derivadas parciales, que
surgen de las ecuaciones físicas (en nuestro caso las ecuaciones de
Maxwell), a ecuaciones diferenciales a derivadas totales, que son más
sencillas de resolver dedicadas a la resolución numérica de las
ecuaciones del electromagnetismo.
Para cada ecuación diferencial a derivadas parciales, hay un número
limitado de sistemas donde la ecuación es separable. Por ejemplo, para
las ecuaciones de Laplace y Helmholtz, que son las esenciales en el
análisis de los problemas electromagnéticos, hay 11 sistemas separables
que corresponden a superficies de coordenada constante en la forma de
cuádricas confocales. De estos sistemas los más conocidos y usados en
la práctica de la ingeniería son los sistemas cartesiano, cilíndrico y
esférico.
7.5.1 SISTEMA CARTESIANO
Figura 48. Sistema de Coordenadas Cartesiano
Es el sistema de coordenadas más común que existe. En este sistema la
posición de un punto P en el espacio se describe mediante las
proyecciones del vector posición sobre tres ejes rectos mutuamente
perpendiculares que se cruzan en el origen de coordenadas:
En éste sistema, el punto P corresponde al punto de intersección de los
tres ejes, indicando la posición del punto en el espacio.
7.5.2 SISTEMA DE COORDENADAS CILÍNDRICO
En el sistema cilíndrico, la posición de un punto P en el espacio se
describe mediante las proyecciones del vector posición sobre un eje
recto (que habitualmente se asocia al eje z del sistema cartesiano
correspondiente) y el plano perpendicular al eje que pasa por el origen
de coordenadas y además por el ángulo formado por la proyección sobre
el plano y un eje recto del plano que pasa por el origen de coordenadas
(que habitualmente se asocia al eje x del sistema cartesiano
correspondiente):
Figura 49. Sistema de Coordenadas Cilíndrico
Las superficies de coordenada constante son en este caso planos
"horizontales" normales a la coordenada z constante, planos "verticales"
que contienen al eje z para la coordenada
constante y cilindros
coaxiales de radio variable
y eje coincidente con z, como el indicado
en la figura 49. Este sistema es uno de los más utilizados para la
descripción y cuantificación de campos electromagnéticos.
7.5.3 SISTEMA ESFÉRICO
Figura 50. Sistema de Coordenadas Esféricos
En el sistema esférico la posición de un punto P en el espacio se
describe mediante el módulo del vector posición y los ángulos que forma
con dos ejes perpendiculares que pasan por el origen de coordenadas,
que coinciden con los ejes z y x del sistema cartesiano correspondiente.
Las superficies de coordenada constante son en este caso conos de eje z
y cuyo vértice pasa por el origen de coordenadas para
constante,
planos "verticales" que contienen al eje z para la coordenada
constante y esferas de radio variable r y origen en el origen de
coordenadas, como la indicada en la figura.
En un sistema de coordenadas, los vectores se expresan por sus
componentes escalares y los vectores asociados a cada coordenada:
Figura 51. Diferentes tipos de vector posición
En el sistema cartesiano los vectores son constantes (no dependen de la
posición). En los sistemas cilíndrico y esférico los vectores sí dependen
de la posición.
7.6 DIAGRAMA DE RADIACIÓN
Un diagrama de radiación es un esquema que utiliza una gráfica en
coordenadas polares representando intensidades de campo (eléctrico y
magnético) o densidades de potencia en diversas posiciones en relación
con una antena.
Cuando el diagrama corresponde al esquema de intensidad de campo
eléctrico (E) o densidad de potencia (P) se denomina gráfica de
radiación absoluta, en donde se considera que la potencia es fija y la
variable de cambio es la distancia; en caso contrario se denomina
radiación relativa en la cual la potencia será variable y la distancia será
fija.
Aunque las gráficas de radiación son bidimensionales la radiación en una
antena es un esquema tridimensional, pero con el fin de facilitar su
análisis se realizan cortes mediante planos horizontales o verticales para
analizar los parámetros de radiación producidos por una antena en una
forma más sencilla.
Figura 52. Ejemplos de diagramas de Radiación
7.7 RESISTENCIA DE RADIACIÓN
Es la resistencia ofrecida por la antena al paso de la corriente alterna;
ésta resistencia es posible calcularla a través de la siguiente expresión:
Rr
PRAD
i2
Otro parámetro importante es la eficiencia de la antena, la cual consiste
en la relación de potencia irradiada por ella sobre la potencia total
(Potencia irradiada + potencia disipada).
PRAD
* 100
PENT
Eficiencia de la antena
PRAD Potencia irradiada (Watts)
PENT Potencia de entrada (Watts)
PD Potencia Disipada (Watts)
PRAD
PRAD
PD
* 100
Expresando la eficiencia en términos de resistencia
i 2 * Rr
i 2 * ( Rr Re )
Rr
Resistencia de Radiación
Re
Resistencia efectiva de la antena
Rr
( Rr
Re )
7.8 GANANCIA DIRECTIVA Y GANANCIA DE POTENCIA
La ganancia directiva es la relación de la densidad de potencia irradiada
hacia una dirección particular entre la densidad de potencia irradiada al
mismo punto pero por una antena de referencia, con la condición de que
ambas antenas deben estar irradiando la misma cantidad de potencia.
Para estos casos se asume que el tipo de antena utilizado es una antena
isotrópica. Cuando la ganancia directiva se considera máxima se le
denomina directividad.
Figura 53. Representación gráfica sobre la Directividad
La ganancia de potencia es lo mismo que la ganancia directiva salvo que
se utiliza es la potencia total de la antena teniendo en cuenta para ello
la deficiencia de la antena y que la antena de referencia no presenta
ningún tipo de pérdidas. Si la antena en mención se considera como una
antena sin pérdidas se dice que la antena irradia el 100 % de la
potencia de entrada concluyendo en ese caso particular que la ganancia
de potencia y la ganancia directiva son iguales. Comúnmente la
ganancia de potencia es expresada en decibelios.
La expresión que permite calcular la ganancia directiva o directividad
D
P
PREF
D Ganancia directiva
P Densidad de potencia en un punto con respecto a una antena
particular (Watts/m2)
PREF Densidad de potencia en el mismo punto con una antena de
referencia (Watts/m2)
La expresión para la ganancia de potencia es:
AP
D*
7.8.1 POTENCIA ISOTRÓPICA EFECTIVA IRRADIADA
La EIRP o potencia isotrópica efectiva irradiada se define como la
potencia equivalente de transmisión es decir es aquella potencia que
debería irradiar una antena isotrópica para alcanzar la misma densidad
de potencia en la dirección elegida y en un determinado punto que en
otra antena. Para calcular la densidad de potencia en un determinado
punto a una distancia R de la antena transmisora, se puede utilizar:
EIRP
PRAD * DT
PRAD Potencia irradiada (Watts)
DT Ganancia directiva de la antena de Transmisión
Otra forma de expresar la potencia Isotrópica, en función de la potencia
de entrada y la ganancia de potencia de la antena es:
EIRP
PENT
AT
PENT * AT
Potencia total de entrada (Watts)
Ganancia de potencia de la antena de Transmisión
Para calcular la densidad de potencia en un punto distante de la antena
transmisora a una distancia R, se logra por la siguiente expresión:
P
PENT * AT
4 R2
PRAD * DT
4 R2
Potencia irradiada (Watts)
Potencia de entrada (Watts)
AT Ganancia de potencia de la antena de Transmisión
DT Ganancia directiva de la antena de Transmisión
R=Distancia de un punto a la antena transmisora
PRAD
PENT
Ejemplo:
Se tiene una antena transmisora la cual presenta las siguientes
características: Ganancia de Potencia AT 20, Potencia de entrada
PENT 100w. Calcular:
a.
b.
c.
EIRP
Densidad de potencia en un punto distante a 15km de la antena
Densidad de potencia para una antena isotrópica
Solución:
a.
Para calcular EIRP se aplica la siguiente expresión:
EIRP
b.
es:
PENT * AT
100 * 20
2000 W
La densidad de potencia con respecto a un punto ubicado a 15km
P
PENT * AT
4 R2
100 * 20
4 (15000 ) 2
0.707 W / m 2
c.
En el caso de utilizar una antena isotrópica, la densidad de
potencia a 15km es 10 veces menor que la obtenida anteriormente. Para
obtener la misma densidad de potencia es necesario que la antena
isotrópica irradie 10 veces la potencia de la anterior antena, es decir,
1000w.
Ejemplo:
Se tiene una antena de transmisión con resistencia de radiación
Rr 72 , una resistencia efectiva Re 8 , una ganancia directiva D=20
y una potencia de entrada PENT 80W. Calcular:
a.
b.
c.
d.
Eficiencia de la antena
Ganancia de la antena
Potencia de radiación
EIRP
Solución:
a. La eficiencia de la antena se puede calcular utilizando la expresión:
Rr
( Rr
Re )
72
72 8
0 .9
90 %
b. Para calcular la ganancia de la antena
AP
D*
=20*0.9=18
c. La potencia irradiada es:
PRAD
PENT
PRAD
PENT *
80 * 0.9
72W
d. EIRP
EIRP
PENT * AT
80 *18
1440 W
7.9 DENSIDAD DE POTENCIA CAPTURADA
Una de las principales características de una antena consiste en su
capacidad para radiar y con una cierta direccionalidad, es decir, para
lograr concentrar la energía radiada hacia ciertas direcciones del espacio
según sea necesario. Para ello, es conveniente cuantificar este
comportamiento con un parámetro que permita establecer una
comparación entre distintas antenas.
Uno de los datos importantes para establecer éste cálculo es conocer
dónde está situada la antena que se desea analizar; en cuyo caso es
conveniente el uso de un sistema de coordenadas que permita definir
cómodamente una dirección del espacio por tal razón el sistema de
coordenadas por excelencia es el esférico. Las tres variables de un
sistema esférico son (r, θ, φ).
Figura 54. Esquema del Sistema de Coordenadas Utilizado
Una antena, es un dispositivo reciproco debido a que presenta la misma
resistencia de radiación, ganancia y directividad cuando se envían o
reciben ondas electromagnéticas, por lo tanto, se puede decir que la
densidad de potencia recibida o capturada por una antena corresponde
al producto de la densidad de potencia en el espacio que la rodea por su
ganancia directiva, es decir, la densidad de potencia en el espacio es
expresada en watts por metro cuadrado.
La expresión que permite calcular la densidad de potencia capturada es:
C
PENT * AT * AR
4 R2
C Densidad de potencia capturada (W/m2)
PENT Potencia de entrada (Watts)
AT Ganancia de potencia de la antena de Transmisión
R Distancia entre las antenas transmisora y receptora
AR Ganancia de potencia de la antena de Recepción
7.9.1 POTENCIA CAPTURADA
La potencia capturada es aquella disponible en los terminales de salida
de una antena, esta potencia puede ser entregada a totalidad en una
carga o una línea de transmisión; esta potencia, es directamente
proporcional a la densidad de potencia recibida y al área de captura de
la antena receptora para determinar el área de captura de una antena
se puede utilizar la siguiente expresión la cual relaciona la capacidad de
capturar energía electromagnética y el tamaño de la antena.
Para calcular el área efectiva de captura se utiliza la siguiente expresión:
AC
AR *
4
2
Ganancia de potencia de la antena de Recepción
Longitud de onda
AC Área efectiva de captura (m2)
AR
Con base en la expresión anterior, para calcular la potencia capturada
por la antena se hace uso de la siguiente expresión:
PCAP
PCAP
P * AC
PENT * AT * AR *
16 * ( R) 2
2
Potencia capturada (Watts)
Potencia de entrada (Watts)
AT Ganancia de potencia de la antena de Transmisión
R Distancia entre las antenas transmisora y receptora (metros)
AR Ganancia de potencia de la antena de Recepción
Longitud de onda (metros)
PENT
7.10 ABERTURA DEL HAZ DE LA ANTENA
La abertura del haz de la antena es el ángulo comprendido entre dos
puntos de media potencia (-3 dB) en el lóbulo mayor de la gráfica de
radiación en una antena.
La ganancia de una antena es inversamente proporcional a la abertura
del haz esto significa que entre más grande sea la abertura del haz
menor será la ganancia.
Figura 55. Abertura del haz de una Antena
Para el caso particular de una antena omnidireccional (isotrópica), la
cual irradia en todas direcciones de igual forma presenta una ganancia
de 1 y una abertura del haz de 360º; en el caso de antenas comunes se
pueden encontrar abertura de haz desde 30º a 60º.
CAPÍTULO 8. TIPOS DE ANTENAS
8.1 ANTENAS BÁSICAS
8.1.1 DOBLETE ELEMENTAL
El doblete elemental o dipolo corto, es el tipo más sencillo de antena
que existe; el termino corto significa que es inferior a media longitud de
onda, aunque físicamente es difícil su construcción es útil para
comprender antenas más prácticas.
Figura 56. Esquema y diagramas de radiación de un doblete
elemental
En éste tipo de antena se puede considerar una corriente variable en el
tiempo según la siguiente expresión:
i(t)=Corriente instantánea
I=Amplitud pico de la corriente de RF (amper)
Angulo de fase (radianes)
f Frecuencia (hertz)
t Tiempo instantáneo (segundos)
De acuerdo con las ecuaciones de Maxwell, el campo de radiación en un
punto lejano es:
E Intensidad del campo eléctrico (volts/metro)
L=Longitud de extremo a extremo del dipolo (metros)
R Distancia del punto al dipolo (metros)
I Corriente del dipolo (amper rms)
Longitud de onda (metros)
Angulo entre el eje de la antena y la dirección de radiación
La densidad de Potencia relativa se calcula de la siguiente forma:
P
E2
120
8.2 DIPOLO DE MEDIA ONDA
Figura 57. Apariencia física de un dipolo de media onda
El dipolo lineal de media onda es el tipo más común de antena para
frecuencias superiores a 2 MHz también llamada antena de Hertz.
Este tipo de antena es una antena resonante, esto significa, que tiene
un múltiplo de cuartos de longitud de onda de largo y un circuito abierto
en los extremos lejanos.
En éste tipo de antena, cada polo es visto como un tramo
correspondiente a una línea de transmisión de un cuarto de longitud de
onda, presentándose en él máximos de voltaje y corriente en sus
extremos y valores mínimos en la parte media. De acuerdo con lo
anterior, su impedancia varía, obteniéndose un valor máximo en los
extremos aproximadamente de 2500 Ω hasta un valor mínimo ubicado
en el punto de alimentación entre 68 Ω y 70 Ω.
8.3 ANTENA MONOPOLO O DE MARCONI
Figura 58. Apariencia física de una antena monopolo
Consiste en un tipo de antena de un cuarto de longitud de onda de
largo, colocada en posición vertical, en donde uno de sus extremos se
encuentra conectado a tierra o en forma directa al suelo. Sus
características son muy semejantes a las de la antena de dipolo de
media onda, presentando máximos valores de corriente y voltaje en sus
extremos, en particular, sobre el extremo aterrizado.
Las pérdidas en éste tipo de antenas se relacionan directamente con el
tipo del terreno donde se encuentra la antena aterrizado, es decir, si el
terreno es buen conductor (arcilloso) o mal conductor (arenoso), en
donde para reducir las pérdidas es necesario implementar un sistema de
polo a tierra mejorando la calidad y humedad del terreno a través de
técnicas y materiales especiales.
8.4 CONJUNTO O RED DE ANTENAS
Un conjunto de antenas o red de antenas se construye combinando dos
o más elementos de una antena para formar una sola antena. Todo
elemento de antena es un radiador o antena individual organizada de tal
forma que sus campos de radiación interactúen entre si provocando una
distribución optima de toda la radiación equivalente a la suma vectorial
de sus campos magnéticos y eléctricos individuales. Este tipo de
arreglos se usa comúnmente para aumentar la directividad de un
sistema de antenas y concentrar la potencia irradiada en un área
geográfica más pequeña.
Figura 59. Apariencia física de algunas agrupaciones de antenas
En esencia, hay dos tipos de elementos de antenas: excitación y de
parasítico (no excitado). Todo elemento excitado es aquel que se puede
conectar directamente con la línea de transmisión recibiendo la potencia
o energía directamente de la fuente.
Los elementos parasíticos son todos aquellos que no se conectan
directamente con la línea de transmisión solo reciben su energía
mediante procesos de inducción mutua con un elemento excitado; los
elementos parasíticos que son de mayor tamaño que los elementos
excitados, se les denomina comúnmente reflectores.
El termino reflector obedece a la propiedad de comportarse como un
espejo cóncavo reflejando la intensidad de la señal en dirección
contraria a como fue recibida provocando con ello la anulación del
campo eléctrico en una dirección y reforzándolo en el otro. Cuando un
elemento parasítico es más corto que un elemento excitado se le
denomina director aumentando con ello la intensidad de campo en su
dirección y reduciéndola en dirección opuesta.
Dentro de los tipos más importantes de redes de antena se pueden
mencionar: red de radiación lateral, red de radiación longitudinal y
antena rómbica.
A continuación se ilustran algunos patrones de radiación que se pueden
obtener utilizando arreglos o redes de antenas.
Figura 60. Algunos patrones de Radiación para redes de antenas
Las antenas individuales generan diagramas de radiación que no
siempre satisfacen las necesidades. Es posible modificar el diagrama de
radiación usando múltiples radiadores, causando interferencia entre los
campos emitidos por cada uno. Para ello es necesario que los radiadores
emitan en forma coherente, es decir, que haya una correlación de fase
entre los campos, lo que se logra habitualmente estableciendo una
correlación de fase entre las corrientes alimentadoras de los radiadores.
Estas disposiciones se conocen como redes o arreglos de radiadores, y
la mayoría de las antenas de uso actual se basan en ellas.
Figura 61. Red de antenas
8.4.1 RED DE RADIACIÓN LATERAL
Figura 62. Antena de radiación lateral:
(a) Red de radiación lateral (b) Gráfica de radiación
Es uno de los tipos más sencillos de redes de antenas se constituye por
varios dipolos resonantes de diferentes tamaños tanto en longitud como
en diámetro paralelos entre si y organizados en línea recta; este tipo de
antena irradia en ángulo recto con respecto al plano del conjunto. En
este tipo de arreglo de antenas la línea de transmisión se conecta en
forma de zigzag produciendo con ello corriente de los elementos en fase
y la radiación de las señales se hace en forma aditiva.
8.4.2 RED DE RADIACIÓN LONGITUDINAL
Figura 63. Antena de radiación longitudinal:
(a) Red de radiación longitudinal (b) Gráfica de radiación
Es otro tipo de arreglo de antenas el cual mantiene en esencia la misma
configuración de los elementos de la red de radiación lateral pero en
este caso la línea de transmisión no se conecta en zigzag como
consecuencia de ello los campos son aditivos y alineados con relación al
plano del conjunto.
8.4.3 ANTENA RÓMBICA
Figura 64. Antena rómbica: (a) Red rómbica (b) Gráfica de radiación
Este tipo de antena es no resonante, funciona óptimamente para anchos
de banda relativamente grandes, lo que la hace ideal para transmisiones
de HF (de 3 a 30 MHz). Esta constituida por cuatro elementos no
resonantes, cada uno de longitud de onda diferente. Este sistema
finaliza en un resistor, cada conjunto de elementos funciona como si
fuera una línea de transmisión terminada en su impedancia
característica provocando con ello que las ondas solo sean irradiadas
hacia delante. La función del resistor consiste en absorber más o menos
la tercera parte de la potencia total de entrada a la antena.
8.5 ANTENAS DE USO ESPECIAL
8.5.1 DIPOLO DOBLADO
Es un tipo de antena constituido por dos elementos, uno de ellos se
alimenta en forma directa mientras que el otro presenta un
acoplamiento inductivo en los extremos, cada elemento posee media
Figura 65. Representación de un Dipolo Doblado
longitud de onda de largo, la corriente de entrada es la mitad
correspondiente a un dipolo básico de media onda y su impedancia
básica es cuatro veces mayor, la impedancia de entrada de un dipolo
doblado es igual a la impedancia de un dipolo de media onda (72 Ω)
multiplicado por la cantidad de alambres doblados elevado al cuadrado.
En esencia es una estructura formada por dos dipolos paralelos,
cortocircuitados en su extremo. Uno de ellos se alimenta en el centro
con un generador.
Una de las principales características del dipolo doblado es que permite
un mayor ancho de banda que un dipolo básico de media onda con la
posibilidad de aumentar el ancho de banda aumentando el diámetro de
los elementos existentes en el dipolo. Se puede descomponer en el
modo par o modo antena, con la misma alimentación en los dos brazos,
y el modo impar o modo línea de transmisión, con dos generadores con
signos opuestos.
El dipolo doblado equivale a un dipolo simple con un transformador de
relación de tensiones 2:1 conectado a su entrada. El circuito equivalente
es dos impedancias en paralelo, de comportamiento reactivo opuesto
(líneas de transmisión en cortocircuito y en circuito abierto). El ancho de
banda del dipolo doblado es superior a la del dipolo simple, debido a que
las reactancias se compensan. En conclusión, un dipolo doblado,
equivale, desde el punto de vista de radiación a un dipolo simple con
corriente de valor doble, e impedancia 4 veces mayor.
8.5.2 ANTENA YAGI-UDA
Figura 66. Antenas Yagi-Uda
Es una de las antenas más populares la cual utiliza un dipolo doblado
como elemento excitador. Esta constituida por un dipolo y dos o más
elementos parasíticos, es decir, un reflector y dos o más directores.
La distancia entre los elementos comúnmente puede ser de 0.1 a 0.2
longitudes de onda, su directividad típica es de 7 a 9dB, se puede
aumentar el ancho de banda aumentando el numero de dipolos doblados
y su uso mas común es para recepción de señales de VHF comprendidas
entre el rango de 54 a 216 MHz.
El dipolo de media onda tiene una ganancia de apenas 2,1 dBi. Para
alcanzar grandes distancias, el Ingeniero japonés Uda desarrolló una
antena formada por un dipolo de media onda al que le añadió otro
dipolo ligeramente más largo en la parte posterior que funge como
reflector y varios dipolos de longitud ligeramente inferior que actúan
como directores, contribuyendo a enfocar la energía en la misma
dirección. Esta antena fue divulgada por el Profesor japonés Yagi en la
década de los treinta y constituye uno de los modelos más populares por
la facilidad de construcción. La ganancia de la antena se puede
aumentar al incrementar el número de elementos directores, lo cual
está limitado sólo por consideraciones mecánicas. En la banda de 2,4
GHz es fácil obtener ganancias de unos 14 dB.
Frecuentemente estas antenas son recubiertas por una envoltura
transparente a las ondas electromagnéticas que le proporciona
protección contra los elementos denominada radome. Es muy fácil de
construir sobre una amplia gama de frecuencias.
Figura 67. Antena Yagi-Uda para 800 MHz
Figura 68. Patrón de radiación de una antena Yagi-Uda
Figura 69. Antena Yagi-Uda con radome para 2.4 GHz
8.5.3 ANTENA DE TORNIQUETE
Consiste en una antena construida por dos dipolos cruzados de dos o
más reflectores (Yagi 2+2). Los dipolos deben ir desfasados 90º con un
latiguillo de ¼ de onda de 90 Ω. Provocando con ello una distribución de
potencia casi omnidireccional.
Figura 70. Antena de Torniquete
8.5.4 ANTENA LOG–PERIÓDICA
Este tipo de antenas se fundamenta en una estructura física repetitiva,
provocando con ello un comportamiento repetitivo de sus características
eléctricas. Esta constituida por varios dipolos de distinta longitud y
distancia los cuales se alimentan de la misma fuente, la línea de
transmisión se encuentra conectada en zigzag, las longitudes de sus
dipolos y su distancia se relacionan de tal forma que los elementos
adyacentes presentan una relación constante entre si, tal como lo
muestra la siguiente expresión:
R2
R1
R3
R2
R4
R3
1
L2
L1
L3
L2
L4
L3
En otras palabras:
1
RN
RN 1
LN
LN 1
R Distancia entre dipolos (metros)
L Longitud del dipolo (metros)
Relación del diseño
Los extremos de los dipolos se encuentran alineados formando un
ángulo denominado α en casos prácticos se considera α=30º y
0.7,
donde
se denomina la relación del diseño.
Figura 71. Antena Log-Periódica
Una de las principales ventajas de este tipo de antenas consiste en su
independencia en la resistencia de radiación y distribución de radiación
respecto a la frecuencia, brindado relaciones de ancho de bandas
superiores a 10; pueden ser unidireccionales o bidireccionales, tener alta
ganancia directiva y son utilizadas comúnmente en aplicaciones de
comunicaciones de HF y VHF.
La impedancia de ésta antena no es constante, varia en forma periódica
aunque no siempre describe funciones sinusoidales, ésta característica
es observable cuando se grafica en función del logaritmo de la
frecuencia; de allí surge el nombre de “log-periódica”.
La distribución de potencia, la directividad, la ganancia de la antena
entre otros factores importantes también presentan el mismo tipo de
comportamiento.
Para calcular la magnitud de un periodo de frecuencia-logarítmica
depende de la relación de diseño y, si suceden dos máximos
consecutivos en las frecuencias f1 y f2, están relacionadas por la fórmula
Con frecuencia, las antenas de TV anunciadas como de “alta ganancia” o
“alto rendimiento” son antenas logarítmicas periódicas.
8.5.5 ANTENA DE CUADRO
Figura 72. Antena de Cuadro
Consiste en una bobina de una sola vuelta de alambre mucho más corto
que una longitud de onda. Está rodeada por un campo magnético en
ángulo recto con el alambre, la distribución de radiación es homogénea.
Es utilizada comúnmente para aplicaciones de muy baja frecuencia, su
polarización es lineal. Se utilizan para aplicación de comunicaciones
móviles y su impedancia de radiación para una espira pequeña es:
Rr
31200 A 2
4
A= Área de la espira
Sin embargo, en caso de que la antena presente más de una espira
(para aplicaciones de muy baja frecuencia) la impedancia de radiación
será igual a la impedancia de radiación de una vuelta multiplicada por el
número de espiras.
8.5.6 ANTENAS DE CONJUNTO ENFASADO
Consiste en un arreglo de antenas conectadas de forma tal que
interactúan entre sí como una sola antena, cuya característica consiste
en que pueden cambiar su ancho de banda y dirección de radiación en
forma electrónica sin tener que mover físicamente algunas de las
antenas individuales o elementos que hacen parte del conjunto.
La principal ventaja consiste, en que no requieren dentro de su
construcción elementos de antena giratorios sus aplicaciones más
comunes son en radares.
Existen dos tipos básicos de estas antenas: el primero consiste en un
dispositivo de salida con manejo de potencia relativamente alto el cual
es el encargado de suministrar la potencia de transmisión al resto de
antenas pertenecientes al conjunto, el segundo tipo, utiliza más o
menos la misma cantidad de dispositivo de salida variables con menor
potencia que el tipo anterior.
En ambos tipos de conjuntos enfasados, la distribución de la radiación
se selecciona cambiando los retardos en las fases que introduce cada
desfasados permitiendo con ello controlar la potencia requerida para
cada una de las antenas que pertenecen al conjunto.
El principio básico de funcionamiento para este tipo de antenas se
fundamenta en la interferencia entre las ondas electromagnéticas en el
espacio libre, debido a que las energías de las ondas electromagnéticas
de diversas fuentes de radiación ocupan el mismo espacio y al mismo
tiempo provoca un efecto de combinación aditivo o destructivo según la
fase que presente cada señal en un instante dado.
Figura 73. Antena de Elementos Enfasados
8.5.7 ANTENA HELICOIDAL
Figura 74. Antena Helicoidal
Es un tipo de antena de VHF y UHF de banda ancha, ideal en
aplicaciones en donde se desea irradiar ondas electromagnéticas con
polarización circular. Se puede utilizar como un solo elemento o se
puede combinar para modificar los patrones de radiación y polarización,
aumentando con ello la ganancia y disminuyendo el ancho de banda en
el lóbulo primario. Con una antena helicoidal se presenta dos modos de
propagación: normal y axial.
En el modo normal la radiación electromagnética es en ángulo recto con
relación al eje de la hélice. En el modo axial la radiación va en dirección
axial provocando una distribución de banda ancha relativamente
direccional.
La ganancia de una antena helicoidal depende de varios factores tales
como: diámetro de la hélice distancia entre vueltas, frecuencia de
operación y la cantidad de vueltas en la hélice, para antenas comunes
se pueden encontrar desde 3 hasta 20 vueltas con ganancias de 15 a 20
dB.
La expresión que permite calcular la ganancia de una antena helicoidal
es:
AP (dB)
10 * log 15
D
2
NS
AP (dB) Ganancia de potencia de la antena en dB
Longitud de Onda (metros / ciclo)
D Diámetro de la boca de un reflector parabólico (metros)
N Numero de vueltas de la antena
S Paso o separación entre vueltas (metros)
Para calcular la abertura del haz a 3dB en una antena helicoidal se
utiliza la siguiente expresión:
Abertura del haz entre puntos de mitad de potencia (en grados)
8.6 Antenas Omnidireccionales
Las antenas omnidireccionales tienen un diagrama de radiación
constante sobre los 360 grados en el plano, es decir un círculo. Por este
motivo son muy utilizadas en estaciones bases, cuando se quiere cubrir
todas las direcciones. Tanto el dipolo de media onda como la antena de
Marconi son omnidireccionales, pero su ganancia es muy reducida, por
lo que para las estaciones bases se suela buscar antenas que ofrezcan
mayor ganancia, las cuales se pueden construir combinando antenas
elementales en lo que se conoce como “arreglos de dipolos”. La
ganancia de una antena omnidireccional de este tipo es de alrededor de
8 a 12 dBi. Son usadas para implementar enlaces punto a multipunto
(PtMP). Son muy buenas para coberturas de 1 a 5 kilómetros,
especialmente en combinación con antenas altamente directivas en las
instalaciones del cliente. Obsérvese que la ganancia en el plano
horizontal se obtiene disminuyendo la radiación hacia arriba y hacia
abajo, como puede constatarse en la siguiente figura.
Figura 75. Antena Omnidireccional de 6 dBi, con su respectivo
diagrama de radiación vertical
El anterior diagrama de radiación es típico de una antena
Omnidireccional
('Svenska
Antennspecialisten
V06/24').
Una
característica interesante de esta clase de antena es que aunque
irradian 360 grados en el plano horizontal, solamente proveen buena
cobertura a los clientes que están dentro de ± 20º en la vertical. Esto
quiere decir que la antena, no podrá alcanzar clientes que están justo
encima de o debajo de la torre.
8.7 Antenas Sectoriales
Las antenas sectoriales también se emplean en las estaciones bases,
donde ofrecen ventajas adicionales como, mejor ganancia (a expensas
de cubrir una zona más restringida) y posibilidad de inclinarlas para dar
servicio a las zonas de interés. Combinando varias antenas sectoriales
se puede dar cobertura en todo el plano horizontal, con mejor ganancia
que la ofrecida por una omnidireccional, pero a mayor costo.
Normalmente, una antena sectorial tiene una ganancia más alta que las
antenas Omnidireccionales (en el rango de 10 - 19 dBi). Este tipo de
antena se usa generalmente para servir en radios de 15 km.
Un valor común de ganancia para una antena sectorial es de 14 dBi para
un ancho del haz horizontal de unos 90º y un ancho del haz vertical de
20º.
Figura 76. Antena Sectorial de 180º
Una antena sectorial puede ser construida usando una antena
omnidireccional y un reflector en forma de V.
Figura 77. Típico modelo de radiación de una Antena Sectorial
La Figura 77 muestra un típico diagrama de radiación de una antena
sectorial. El diagrama de radiación horizontal muestra que la mayor
parte de la energía es irradiada en la parte frontal de la antena. Una
parte muy pequeña de la energía es irradiada en la parte de atrás de la
antena sectorial. El patrón de radiación vertical es muy similar a una
antena Omnidireccional donde el ancho del haz es muy angosto
normalmente no es más grande que 20º. Típicamente, una antena
sectorial está montada en una torre alta, ligeramente inclinada para
poder servir a un área justo debajo de ella.
Una antena sectorial con alta ganancia necesita
cuidadosamente en lo que respecta al ángulo de inclinación.
montarse
Figura 78. Ejemplo de antena sectorial: Antenn Specialisten
VP870/24 antena de paneles vertical 70°, 16.5 dBi.
¿Por qué necesitamos sectorizar?
Nos permite colocar múltiples puntos de acceso en una torre, y así
ofrecer más ancho de banda
Permite aislar áreas con más alto niveles de ruido de RF
Puede separar enlaces de larga y corta distancia (estabilidad)
8.8 Antena Plana o “Patch”
Esta antena es muy popular porque es visualmente poco impactante. Se
consigue con ganancias de hasta 23 dBi en nuestro rango de frecuencias
y a menudo se pegan a la caja que contiene el radio, en un solo objeto.
Figura 79. Antena Plana
Figura 80. Cubierta externa de una antena plana de 8 dBi
Figura 81. Antena plana de múltiples elementos (Path)
8.9 ANTENAS DE UHF Y MICROONDAS
Figura 82. Tipos de antenas para Microondas
Una de las características que presentan este tipo de antenas es que
deben ser muy direccionales, su ganancia es considerada aparente
debido a que se debe concentrar la potencia irradiada en un haz delgado
para se transmitido de igual forma en todas direcciones.
Para el caso de antenas de microondas, es común encontrar aberturas
de haz a mitad de potencia inferiores a un grado. Las antenas de UHF
se encuentran en el rango de frecuencia entre 0.3 y 3 GHz en el caso de
las microondas entre 1 a 100 GHz.
Las antenas de microondas presentan tres características importantes:
la eficiencia direccional, acoplamiento espalda con espalda y
acoplamiento lado a lado.
La eficiencia direccional o relación de frente a espalda consiste en la
relación de ganancia máxima en dirección delantera con respecto a la
ganancia máxima en dirección trasera; este valor puede ser inferior a 20
dB y es fundamental para el momento de su diseño.
En el caso de los acoplamientos de lado a lado y espalda con espalda,
indican las perdidas por acoplamiento entre antenas se expresan en dB.
Se recomienda que las perdidas por acoplamiento sean altas para evitar
que una señal de transmisión de una antena interfiera con una señal de
recepción de otra antena.
Las antenas de microondas deben ser muy direccionales deben enfocar
su energía en un haz angosto el cual se puede dirigir hacia una antena
receptora prácticamente a línea vista, permite aumentar varias veces la
magnitud de la potencia irradiada a comparación de otro tipo de antenas
en donde el tipo más común de antena tanto para transmisión como
para recepción es el reflector parabólico.
8.9.1 ANTENA DE REFLECTOR PARABÓLICO
Son antenas capaces de proporcionar ganancias y directividad de
radiación extremadamente altas usadas comúnmente para enlaces de
radio y satélite. Esta constituida por dos elementos principales: un
reflector parabólico y un mecanismo de alimentación. Este mecanismo
de alimentación comúnmente es un dipolo o una red de dipolos en
donde se irradian las ondas electromagnéticas hacia el reflector el cual
es el encargado de concentrar y direccionar todas las ondas individuales
enfasadas entre si.
Figura 83. Antena y reflectores parabólicos
El reflector parabólico se considera como el componente más importante
de una antena parabólica, es semejante a un plato y la reflexión que
produce depende de su construcción geométrica la cual es semejante a
una parábola.
Para calcular la abertura del haz de una antena parabólica a -3 Db se
utiliza la siguiente expresión:
70 * c
f *D
70 *
D
Abertura del haz entre puntos de mitad de potencia (grados)
Longitud de Onda (metros/ciclo)
D Diámetro de la boca de un reflector parabólico (metros)
Frecuencia de operación (Hz)
f
c Velocidad de propagación en el espacio libre ( 3 *108 m / s )
Para grandes alcances, el reflector parabólico es el más utilizado porque
permite obtener ganancias de hasta 30 dB a costos razonables. El
reflector puede ser una lámina sólida o perforada, y mientras que las
perforaciones no excedan de una décima parte de la longitud de onda,
su efecto en las prestaciones eléctricas de la antena no será notable,
siendo la resistencia al viento significativamente menor. En algunos
casos el reflector se fabrica con una malla o con una grilla de alambre.
Comercialmente hay varios fabricantes que producen estas antenas y se
consiguen a veces de segunda mano a precios muy atractivos. Como la
frecuencia de operación depende solamente del elemento activo o
alimentador, reflectores utilizados para aplicaciones satelitales a
frecuencias más altas pueden perfectamente ser utilizados a otras
frecuencias dotándolos del alimentador adecuado, como se ilustra en la
figura. Las antenas parabólicas son las preferidas para enlaces a larga
distancia, especialmente en frecuencias de microondas.
Figura 84. Reflector parabólico de malla alimentada con una
antena guía-onda a 2,4 GHz
El diagrama de radiación de una antena parabólica es bastante similar al
de una antena Yagi pero con un ángulo del servicio mucho más angosto.
Debido a que la mayor parte de la energía de RF apunta hacia un área
de servicio muy pequeña, una antena parabólica es mucho más difícil de
apuntar. Por consiguiente, la antena parabólica es más frágil al disturbio
físico y mecánico, el viento es especialmente un problema comparado
con una Yagi.
8.9.2 EFICIENCIA DE UNA ANTENA PARABÓLICA
En el caso de un reflector parabólico, la reflactancia de la superficie del
plato no es perfecta. Esto quiere decir, que una pequeña parte de la
señal irradiada es absorbida por el plato adicionalmente la energía
cercana a las orillas del plato no se refleja.
Un valor aproximado de la cantidad de energía que se puede irradiar
esta entre el 50 y el 75% de la señal irradiada por la fuente. Debido a
estas pérdidas comúnmente se considera que la eficiencia de una antena
parabólica es de un 55 %.
8.9.3 GANANCIA DE POTENCIA DE UNA ANTENA PARABÓLICA
La ganancia de potencia de una antena parabólica es inversamente
proporcional a la longitud de onda elevado al cuadrado por lo cual el
área del plato o reflector. Este parámetro juega un factor importante a
la hora de diseñar antenas parabólicas, el cual depende directamente de
la longitud de onda. La expresión matemática para calcular la ganancia
de una antena transmisora es:
AP
*D
2
AP Ganancia de potencia con respecto a una antena isotrópica
(adimensional)
Eficiencia de la antena: potencia irradiada por la antena en relación
con la potencia irradiada por el mecanismo de alimentación
(adimensional)
D Diámetro de la boca de un reflector parabólico (metros)
Longitud de Onda (metros/ciclo)
Como se considera que la eficiencia de una antena de éste tipo,
normalmente es del 55%, la anterior expresión se reduce a
5.4 * D 2 * f
c2
AP
2
en la que c es la velocidad de propagación, 3x108 m/s. En forma de
decibelios,
AP (dB)
20 * log( f )
20 * log( D)
42 .2
En donde,
AP Ganancia de potencia con respecto a una antena isotrópica
(decibelios)
D Diámetro de la boca de un reflector parabólico (metros)
f
Frecuencia en (megahertz)
42.2 = Constante (decibelios)
Para una eficiencia de antena de 100%, se agregan 2.66 dB al valor
calculado en la anterior ecuación.
Existe un término importante en los reflectores parabólicos denominado
área de captura, la cual es considerada el área real del reflector
encargada de recibir o capturar la mayor parte de la energía
electromagnética y puede ser calculada según la siguiente expresión:
AC
AC
k*A
Área de Captura (metros cuadrados)
k Eficiencia de abertura, la cual depende del tipo de antena y su
configuración. En aplicaciones prácticas éste parámetro puede ser
considerado como 0.55
A = Área real (metros cuadrados)
Con base en lo anterior, la ganancia de potencia para una antena
parabólica receptora será:
AP
4 * * AC
2
5.4
D
2
D Diámetro del plato (metros)
Longitud de Onda (metros/ciclo)
Ejemplo:
Para un reflector parabólico de 2.5 m de diámetro, 10W de potencia
irradiada por la fuente, la frecuencia de funcionamiento es de 7GHz y
con eficiencias de transmisión y eficiencia de abertura del 55%.
Calcular:
a.
b.
c.
d.
Abertura del haz
Ganancia de potencia de Transmisión
Ganancia de potencia de Recepción
Potencia isotropita efectiva irradiada (EIRP)
Solución:
a. La abertura del haz se calcula de la siguiente forma:
70 * c
f *D
70 * 3 *108
(7 *109 ) * (2.5)
1.2 O
b. La ganancia de potencia en la antena de transmisión
AP (dB)
AP (dB)
20 * log( f ) 20 * log( D) 42 .2
20 * log(7000 ) 20 * log(2.5) 42 .2
42 .66 dB
c. La ganancia de potencia en la antena de recepción
3 * 10 8
7 * 10 9
c
f
AP (dB) 10 * log 5.4
D
2
0.043 m / ciclo
2.5
10 * log 5.4
0.043
2
42 .61dB
d.
La EIRP, es el producto de la potencia irradiada por la ganancia de
la antena de transmisión en Decibelios
EIRP
AP (dB) PIRRADIADA(dBm)
42.61 10 * log(
10
)
0.001
82.61dBm
8.9.4 MECANISMOS ALIMENTADORES
Un dispositivo de alimentación es el que se encarga de irradiar la
energía electromagnética de una antena, su función es orientar esta
energía al reflector para ser direccionada hacia un punto particular.
Existen tres tipos principales de antenas parabólicas según el tipo de
alimentación: alimentación central, alimentación cónica y alimentación
de Cassegrain.
8.9.4.1 ALIMENTACIÓN CENTRAL
Es un tipo de antena que utiliza un reflector paraboloide alimentado en
el centro con un reflector esférico adicional; este reflector esférico
adicional contribuye a concentrar más energía en la dirección deseada
que el reflector utilizado convencionalmente, ayudando a bloquear
algunas reflexiones iniciales no deseadas.
Figura85. Antena parabólica con alimentación central
8.9.4.2 ALIMENTACIÓN POR BOCINA
Figura 86. Antena Cónica
Es un tipo de alimentación aplicado a antenas cónicas. La bocina
consiste en un material abocardado de guías de onda el cual es
colocado en el foco de la antena y se encarga de irradiar la potencia en
forma direccional hacia el reflector parabólico, su estructura puede tener
varias formas: piramidal, divergente, entre otros. La dirección de
propagación depende de la abertura de la boca del cuerno la cual se
calcula de la siguiente forma:
E
H
dE
dH
E
56 *
dE
H
56 *
dH
Abertura del haz de media potencia en el plano E (grados)
Abertura del haz de media potencia en el plano H (grados)
Longitud de Onda
Tamaño de la boca en el plano E (metros)
Tamaño de la boca en el plano H (metros)
Una antena de cuerno cónico consiste en un cono que se trunca en un
tramo circular de guía de onda esta guía de onda es conectada a la
antena cumpliendo funciones de una antena adicional, la longitud del
cono esta directamente relacionado con la ganancia de la antena, el
ángulo de conicidad o ángulo de apertura del cono comúnmente es de
50 grados junto con la longitud del cono se deben ajustar para obtener
máximo patrón de radiación en el reflector.
8.9.4.3 ALIMENTACION DE CASSEGRAIN
Consiste en una fuente de radiación primaria ubicada detrás de una
pequeña abertura en el vértice del paraboloide y no en el foco como las
anteriores antenas, esta antena primaria apunta hacia un pequeño
reflector secundario ubicado entre el vértice y el foco.
Los rayos emitidos por la antena primaria se reflejan en el subreflector y
estos a su vez son reflejados hacia el reflector parabólico principal,
ofreciendo con ello una mayor directividad de radiación lo cual los hace
óptimos para la recepción de señales extremadamente débiles o cuando
se requieran líneas de transmisión o tramos de onda extremadamente
largos. El subreflector debe tener una curvatura hiperbólica para reflejar
los rayos de la antena primaria de tal forma que funcione como una
fuente primaria.
CAPÍTULO 9. GUÍAS DE ONDA
9.1 TIPOS DE GUÍAS DE ONDA
Figura 87. Guía de Onda
Una línea de transmisión de hilos paralelos no puede propagar con
eficiencia energía electromagnética, inclusive en cables coaxiales, en
donde la frecuencia de la señal sea superior a 20 GHz. debido a
diferentes factores de atenuación propias de los materiales con los
cuales esta constituida la línea de transmisión. Otra limitante ocurre
cuando se desean propagar señales de alta potencia las cuales no se
pueden propagar por líneas de transmisión convencionales por tal razón
es necesario recurrir a medios físicos de transmisión alternativa capaz
de soportar estas adversidades en formas óptimas tales como: fibra
óptica y guías de onda.
Una guía de onda es un tubo de conductor hueco el cual puede ser
rectangular, circular o elíptico. Sus dimensiones rigen las condiciones
de propagación de ondas electromagnéticas por su interior sirviendo su
periferia como guía de conducción para las ondas, una guía de onda no
conduce corriente en el sentido estricto, más bien, sus paredes son
conductores y permiten reflejar la energía electromagnética en su
superficie.
En una guía de onda la propagación de la energía no ocurre sobre las
paredes sino a través del dieléctrico en el interior el cual en la mayoría
de los casos es aire, la energía electromagnética que viaja por una guía
de onda lo hace en trayectoria de zigzag reflejándose y rebotando sobre
las paredes que las constituyen.
9.1.1 GUÍA DE ONDA RECTANGULAR
Es el tipo de onda más popular que existe. Para que una onda
electromagnética pueda viajar a través de una guía de onda debe ser
capaz de satisfacer las ecuaciones de Maxwell, por tal razón, las ondas
electromagnéticas deben propagarse en el interior de la guía de onda en
forma de zigzag porque si lo hiciera en línea recta el campo eléctrico se
pondría en corto con las paredes de la guía de onda evitando que la
onda se propagara en su interior.
En las líneas de transmisión la velocidad de la onda no depende de su
frecuencia sin embargo existen dos clases de velocidad que se deben
tener en cuenta: velocidad de fase y velocidad de grupo.
La velocidad en fase es la velocidad aparente de una fase determinada
de la onda, es aquella con la que cambia de fase una onda en dirección
paralela a una superficie conductora a continuación se ilustra la
expresión que permite calcular la velocidad de fase la cual depende de la
frecuencia y longitud de onda de la señal.
VPH
fC
f
c
c
1 ( fC / f )2
Frecuencia de corte (Hz)
Frecuencia de operación (Hz)
Velocidad de propagación en el espacio libre ( 3 *108 m / s )
La velocidad de grupo como su nombre la indica, consiste en la
velocidad de un grupo de ondas, es decir, la velocidad con la que se
propaga la energía total de la señal. Las velocidades de grupo y de fase
presentan el mismo valor en el espacio libre o vació y en las líneas de
transmisión de hilos paralelos, sin embargo si son medidas con la misma
frecuencia a través de
una guía de
onda se obtendrán valores
diferentes para cada una.
Una característica particular es que la velocidad de fase siempre será
mayor o igual que la velocidad de grupo y si se multiplican estas dos
velocidades (fase y grupo) su resultado es igual al cuadrado de la
velocidad de propagación en el espacio libre es decir el cuadrado de la
velocidad de la luz.
c2
Vg *VPH
c Velocidad de propagación en el espacio libre ( 3 *108 m / s )
VPH Velocidad de Fase (m/s)
V g Velocidad de grupo (m/s)
La relación entre la longitud de onda en el espacio libre a través de la
guía de transmisión y la velocidad de la onda electromagnética es la
siguiente:
VPH
O
c
g
g
O
Longitud de onda en la guía (metros / ciclo)
Longitud de onda en el espacio libre (metros / ciclo)
c Velocidad de propagación en el espacio libre ( 3 *108 m / s )
VPH Velocidad de Fase (m/s)
9.1.1.1 FRECUENCIA DE CORTE Y LONGITUD DE ONDA DE CORTE
La frecuencia de corte es aquella frecuencia mínima de operación
presente en una guía de onda quiere decir que cualquier frecuencia por
debajo de este valor no se propagara por la guía de onda.
fC
fC
c
a
c
2a
Frecuencia de corte (Hz)
Velocidad de propagación en el espacio libre ( 3 *108 m / s )
Longitud de la sección transversal en metros
La longitud de onda de corte es la longitud de onda máxima posible de
una onda electromagnética que se pueda propagar a través de una guía
de onda. Para efectos prácticos en guías de onda rectangulares, aunque
según el valor de la frecuencia de corte, se pueden propagar ondas
electromagnéticas con frecuencias superiores a esta a través de una
guía de onda, es común restringir el rango de frecuencias de las ondas
electromagnéticas entre la frecuencia de corte y dos veces esta
frecuencia. La relación matemática para calcular la longitud de onda de
corte es la siguiente:
c
o
g
g
1 ( fC / f )2
f
2
fC
2
Longitud de onda en la guía (metros / ciclo)
f
Longitud de onda en el espacio libre (metros / ciclo)
Frecuencia de corte (Hz)
Frecuencia de operación (Hz)
c
Velocidad de propagación en el espacio libre ( 3 *108 m / s )
O
fC
Ejercicio:
Se tiene una guía de onda rectangular con una separación entre paredes
de 3cm y una frecuencia deseada de operación de 7GHz. Calcular:
a. Frecuencia de corte
b. Longitud de onda de corte
c. La velocidad de grupo
d. La velocidad de fase
Solución:
a. Para calcular la Frecuencia de corte se aplica la siguiente expresión
fC
c
2a
3 * 10 8 m / s
2 * (0.03 m)
b. La longitud de onda de corte es:
5GHz
c
fC
C
2a
2(3cm)
6cm
c. La velocidad de fase es:
VPH
3 *108
c
1 ( fC / f )
2
1 (5GHz / 7GHz)
4.286 *108 m / s
2
d. Velocidad de Grupo
Vg *VPH
Vg
c2
VPH
(3 *108 ) 2
4.286 *108
c2
2.1*108 m / s
9.1.1.2 IMPEDANCIA CARACTERÍSTICA
Toda guía de onda presenta una impedancia característica, la cual es
considerada análoga a la de una línea de transmisión de hilos paralelos
y se determina por la siguiente expresión:
ZO
377
1 ( fC / f )2
377
g
O
ZO = Impedancia Característica (Ω)
fC= Frecuencia de Corte
f= Frecuencia de operación (Hz)
Para casos prácticos, ZO es mayor que 377 Ω. Cuando la frecuencia
corresponde a la frecuencia de corte, ZO se vuelve infinita y al doble de
la frecuencia de corte (valor en el cual se restringe el rango máximo de
frecuencia) ZO=435 Ω.
9.1.1.3 BALANCEO DE IMPEDANCIA
Figura 88. Balanceo de impedancias en guías de onda
En las guías de onda es necesario el uso de elementos que permitan el
balanceo o compensación de impedancias de igual forma como ocurre
en las líneas de transmisión de hilos paralelos. Estos acoples deben ser
equivalentes a elementos reactivos tales como: inductancias o
capacitancias. Consisten en diafragmas o laminas metálicas delgadas
instaladas perpendicularmente a las paredes de las guías de onda unidas
a ella en sus orillas formando una abertura. Cuando la abertura es
paralela a las paredes cortas su comportamiento es inductivo pero si las
paredes son largas se considera capacitivo y su valor reactivo es
proporcional al tamaño de la abertura.
9.2 GUIA DE ONDA CIRCULAR
Cuando se presentan aplicaciones en donde es necesario propagar
ondas polarizadas vertical y horizontalmente por la misma guía de onda.
Tal como ocurre en aplicaciones de radar y microondas, es necesario el
uso de guías de ondas circulares. Su comportamiento es igual que el de
las guías rectangulares, sin embargo, la longitud de onda de corte se
calcula por la siguiente expresión:
O
1 .7 d
d: Diámetro de la guía de onda (metros)
Una de las principales ventajas de las guías de ondas circulares sobre
las rectangulares es que son más fáciles de fabricar y de empalmar.
Entre las desventajas está un área mucho mayor; complementándose
con el hecho de que una onda que viaja por una guía de onda circular
con polarización horizontal podría cambiar a polarización vertical y
viceversa.
Figura 89. Antena Guía de onda hecha con un tubo de desagüe.
Se está conectando a 10 km de distancia.
La antena de la figura 89, es de la más fácil de construir para la banda
de 2,4 GHz y presenta un excelente rendimiento, con ganancias de
hasta 12 dBi.
9.3 GUÍA DE ONDA RÍGIDA
La figura 90, muestra dos clases de guía de onda rígida. Esta clase de
guías es más costosa en su fabricación que las rectangulares normales;
sin embargo, permite también el funcionamiento a menores frecuencias,
para determinado tamaño. En consecuencia, es posible tener menores
dimensiones generales de guía de ondas cuando son con entrantes. Esta
característica, combinada con su mayor costo, limita su utilidad a
aplicaciones especializadas.
Figura 90. Guía de onda rígida. (a) un entrante; (b) doble entrante
9.4 GUÍA DE ONDA FLEXIBLE
La figura 91, muestra un tramo de una guía de ondas rectangular
flexible. Consiste de bandas en espiral, de latón o cobre. El exterior
esta recubierto con un dieléctrico suave, normalmente de hule, para
mantener hermética la guía de onda al aire y al agua. En los sistemas de
microondas se usan tramos cortos de guía de onda flexible, cuando se
interconectan varios transmisores y receptores con una unidad compleja
de combinación o de separación. También, se utilizan mucho las guías
de onda flexibles en los equipos de prueba de microondas.
Figura 91. Guía flexible de ondas
9.5 ANTENA DE RANURA
Puede parecer paradójico que una ranura u orificio pueda funcionar
como antena. Sin embargo, cuando se tiene una guía de onda, una
ranura de media longitud de onda se comporta exactamente como un
dipolo de media onda. Combinando de manera adecuada varias de estas
ranuras se puede obtener diferentes patrones de radiación, incluyendo
antenas sectoriales de 180º o inclusive omnidireccionales. En
http://www.trevormarshall.com/waveguides.htm,
encontrará
una
descripción completa de como construir este tipo de antenas.
Figura 92. Antena de Ranura
9.6 LA CARTA DE SMITH
La Carta de Smith es un método gráfico para calcular parámetros de
impedancia, admitancia entre otros, orientado hacia antenas y líneas de
transmisión. Fue desarrollada por PHILIP H. SMITH en 1939 y se
fundamenta en dos conjuntos de círculos ortogonales. El primer
conjunto representa la relación del componente resistivo de la
impedancia de la línea (R) a la impedancia característica de la línea
(Zo). El segundo conjunto representa la relación del componente
reactivo de la impedancia de la línea (jX) entre la impedancia
característica de la línea (Zo).
ZO
R
jX
Con la carta de Smith es posible graficar y calcular los siguientes
parámetros:
1. Atenuación entre dos puntos cualesquiera
Coeficiente de pérdida de una onda estacionaria
Perdidas por reflexión).
2. Longitud de la línea de transmisión entre dos puntos cualesquiera
expresado en longitudes de onda
3. La impedancia o admitancia en cualquier punto a lo largo de la línea
de transmisión
Magnitud del coeficiente de reflexión
Angulo del coeficiente de reflexión)
4. Relación de ondas estacionarias de voltaje o corriente
Relación de onda estacionaria
Limites de voltaje y corriente debido a ondas estacionarias
Como es sabido la impedancia de una línea de transmisión es compleja,
esto quiere decir que esta conformada por componentes reales e
imaginarias, en donde la parte real representa el componente resistivo y
la parte imaginaria el componente reactivo.
Uno de las consideraciones a tener en cuenta a la hora de trabajar en la
carta de Smith, consiste en que esta se fundamenta en el coeficiente de
reflexión compleja de acuerdo con la siguiente expresión:
z 1
z 1
Donde z corresponde a la impedancia normalizada a la impedancia
característica, es decir:
z
ZL
ZO
Con base en lo anterior, z podrá tomar valores entre 0 y 1, lo mismo
sucede con el valor del coeficiente de reflexión. Cuando z=1,
0;
sucede que la impedancia de carga es igual a la impedancia
característica (caso ideal).
Cuando se desea analizar la carta de Smith imaginémonos un plano
cartesiano en donde el eje horizontal de la carta representa el
componente resistivo y el eje vertical representa el componente
reactivo. Si el punto se encuentra sobre el eje vertical por encima del
eje horizontal representara valores positivos de reactancia equivalentes
a un comportamiento inductivo, de lo contrario, si el punto se encuentra
por debajo del eje horizontal representara valores negativos de
reactancia y su equivalente es un comportamiento capacitivo.
Figura 93. Diagrama de Coordenadas en la carta de Smith
La carta de Smith consiste en la representación gráfica, en el plano del
coeficiente de reflexión, de la resistencia y la reactancia normalizadas.
Esta herramienta gráfica permite la obtención de diversos parámetros
de las líneas de transmisión y la resolución de problemas de adaptación
de impedancias, evitando las operaciones con números complejos que
suelen implicar estos cálculos.
9.6.1 GRÁFICA DE IMPEDANCIAS EN LA CARTA DE SMITH
Para comprender mejor cómo graficar impedancias sobre la carta de
Smith es mejor hacerlo a través de un ejemplo.
Ejemplo 1:
Graficar en la carta de Smith una impedancia Z L
cuenta una impedancia característica Z O 50
20 , teniendo en
Solución:
Para graficar sobre la carta de Smith la impedancia en cuestión, lo
primero que se debe hacer es calcular la impedancia normalizada (z)
z
ZL
ZO
20
50
0,4
En el dibujo se observa el punto z, ubicado sobre el eje horizontal (R), el
cual representa el componente resistivo. Como en éste caso particular,
la impedancia normalizada tiene como valor 0,4 presentando solamente
un valor real, basta simplemente con identificar el circulo
correspondiente a la carta de Smith que tiene como valor 0,4 ubicando
el punto z en la zona donde éste circulo corta al eje R.
Nota: Vale la pena aclarar, que aunque la carta de Smith presenta una
gran cantidad de círculos de diferentes valores, solamente en el dibujo
por comodidad se ilustran los círculos correspondientes a 0, 0.2, 0.5,
1.0 y 2.0. El círculo que corresponde al valor de 0 es el círculo más
externo de la carta.
Ejemplo 2:
Graficar en la carta de Smith una impedancia Z L
cuenta una impedancia característica Z O 50
j 25 , teniendo en
Solución:
Nuevamente, para graficar sobre la carta de Smith la impedancia en
cuestión, lo primero que se debe hacer es calcular la impedancia
normalizada (z)
z
ZL
ZO
j 25
50
j 0,5
Como en éste caso, la impedancia normalizada no presenta componente
real o resistivo el valor de R=0, perteneciendo en la carta al circulo más
externo. Adicionalmente, teniendo en cuenta que el valor de la
impedancia arrojo una cantidad imaginaria positiva corresponde a una
impedancia inductiva. En caso de haber resultado negativa sería una
impedancia capacitiva.
Con base en la distribución de los parámetros en la carta de Smith, la
ubicación de las cantidades positivas imaginarias se encuentra en el
hemisferio superior de la carta. Por tal razón, nos ubicamos sobre el
valor 0 del eje horizontal (R) y nos desplazamos sobre éste círculo en
sentido de las manecillas del reloj hasta el valor (j0,5) en donde se
encuentra localizado el valor de z tal como se ilustra en la figura.
Ejemplo 3:
Graficar en la carta de Smith una impedancia Z L
cuenta una impedancia característica Z O 50
20
j 25
, teniendo en
Solución:
Nuevamente, para graficar sobre la carta de Smith la impedancia en
cuestión, lo primero que se debe hacer es calcular la impedancia
normalizada (z). Observemos que ésta vez el valor de la impedancia a
graficar presenta componente real y componente imaginario, lo que
indica valores Resistivos y Reactivos.
z
ZL
ZO
20
j 25
50
0,4
j 0,5
En éste nuevo caso, el resultado de la impedancia normalizada arrojo un
valor de 0,4 para el eje Resistivo y j0,5 para el eje Reactivo. Se debe
identificar primero el círculo que corresponde al valor R=0,4 que para el
caso se dibujo de color amarillo y luego, como el componente reactivo
es positivo y de valor j0,5 sobre el circulo amarillo nos desplazamos en
sentido hacia las manecillas del reloj hasta encontrar el punto que se
corte con el circulo que pertenece al valor j0,5; en donde finalmente se
encuentra el punto z tal como se ilustra en la figura. Si el componente
reactivo hubiera sido negativo, nos desplazaríamos sobre el mismo
círculo amarillo pero en sentido contrario, es decir, en contra de las
manecillas del reloj.
9.6.2 GRÁFICA DE ADMITANCIAS EN LA CARTA DE SMITH
Para comprender mejor cómo graficar admitancias sobre la carta de
Smith es mejor hacerlo nuevamente a través de un ejemplo. Para
calcular y graficar Admitancias, primero se deberá calcular la
impedancia normalizada y después de ubicar el respectivo valor sobre la
carta se dibujará un círculo desde el punto z con centro en el punto
(1,0), en donde finalmente se traza una línea desde el punto z con
respecto al valor (1,0) en la carta de Smith y prolongarla hasta que se
corte con algún punto que corte el circulo dibujado. Ese punto
corresponderá al valor de la admitancia normalizada de z. Con esto se
quiere decir que el valor de la admitancia se calculará dando un giro de
180 grados con respecto al valor de z tomando como centro o referencia
el punto (1,0) sobre la carta de Smith.
Ejemplo 1:
Graficar en la carta de Smith una impedancia para Z L
cuenta una impedancia característica Z O 50
20 , teniendo en
Solución:
Para graficar sobre la carta de Smith la admitancia en cuestión, lo
primero que se debe hacer es calcular la impedancia normalizada (z)
z
ZL
ZO
20
50
0,4
En el dibujo se observa el punto z, desde el cual se traza un círculo con
centro en el punto (1,0) identificado con el color amarillo. Después de
dibujado el circulo, se traza una línea que une el punto z con el punto
(1,0) y se prolonga hasta que ésta línea corte el circulo amarillo
nuevamente en donde se encuentra ubicada la Admitancia de z
etiquetada como (y).
En éste caso según la carta, y está ubicada aproximadamente sobre el
punto (2.5, 0)
Calculando matemáticamente el valor de la admitancia se obtiene:
y
1
z
1
0,4
2,5
Observando el valor calculado de la admitancia con el obtenido
gráficamente coincide. Verificándose con ello el método gráfico sobre la
carta de Smith para calcular admitancias.
La admitancia obtenida hasta el momento corresponde a la admitancia
normalizada. Para obtener el valor real de la admitancia, basta con
dividir el valor de la admitancia normalizada por el valor de la
impedancia característica Zo.
Y
y
ZO
2,5
50
0,05
Ejemplo 2:
Graficar en la carta de Smith la admitancia para Z L
en cuenta una impedancia característica Z O 50
20
j 25
, teniendo
Solución:
Nuevamente, para graficar sobre la carta de Smith la admitancia en
cuestión, lo primero que se debe hacer es calcular la impedancia
normalizada (z).
z
ZL
ZO
20
j 25
50
0,4
j 0,5
Realizando el mismo procedimiento anterior. Primero ubicamos el punto
z, después se dibuja un círculo desde el punto z con centro en el punto
(1,0) y finalmente, se traza una línea que una el punto z con el punto
(1,0) hasta que se corte con algún punto sobre el círculo dibujado.
Analizando el resultado del procedimiento anterior, se puede observar
que el punto y se toca con el circulo perteneciente al valor de R=1 y que
aproximadamente coincide con el circulo reactivo (de color azul) cuyo
valor es –j0,2.
Matemáticamente el valor de la admitancia es:
y
1
z
1
0,4
j 0,5
0,97
j1,21
Lo cual corrobora el resultado obtenido gráficamente.
Por lo tanto, el valor real de la admitancia será:
Y
y
ZO
0,97
j1,21
50
0,019
j 2,44 * 10
2
9.6.3 GRAFICAR EL SWR EN LA CARTA DE SMITH
Hasta el momento se ha explicado cómo es el proceso para graficar y
calcular impedancias y admitancias. Sin embargo, no son lo únicos
parámetros que se pueden obtener a través de la carta de Smith.
A continuación se explica el procedimiento para calcular el parámetro
SWR denominado Relación de Onda Estacionaria.
El procedimiento es muy semejante a los anteriormente expuestos y que
de igual forma es más fácil explicarlo a través de un ejemplo.
Para calcular el factor SWR, primero se deberá calcular y graficar el
valor z correspondiente a la impedancia normalizada. Después de
graficado éste punto, se dibujará un circulo desde el punto z con centro
en el punto (1,0) al igual que ocurría al calcular la admitancia; sin
embargo, la diferencia radica en que ésta vez no se trazará una línea
desde el punto z, sino que se buscará el punto sobre el cual éste circulo
corta al eje horizontal (R) y el valor de R en ese punto será igual al valor
de SWR.
Ejemplo 1:
Graficar en la carta de Smith el valor SWR para Z L
cuenta una impedancia característica Z O 50
20 , teniendo en
Solución:
Para graficar sobre la carta de Smith el parámetro SWR en cuestión, lo
primero que se debe hacer es calcular la impedancia normalizada (z)
z
ZL
ZO
20
50
0,4
Después de calculado y graficado el punto z, se traza un circulo con
centro en el punto (1,0) identificado con color amarillo. Ahora, se busca
el punto en el cual éste circulo corta el eje R. en éste caso particular
SWR=2.5 tal como se ilustra en la gráfica.
9.6.4 CÁLCULO DE LA IMPEDANCIA DE ENTRADA EN UNA LINEA
DE TRANSMISIÓN UTILIZANDO LA CARTA DE SMITH
Utilizando la carta de Smith es posible calcular la impedancia de entrada
en una línea de transmisión a cualquier distancia de la carga, indicando
la distancia deseada en función de la longitud de onda.
Para comprender mejor éste proceso es importante observar que en la
carta de Smith existen dos escalas externas a la carta las cuales indican
distancias en longitudes de onda.
La escala externa muestra la distancia de la carga al generador, la cual
aumenta en dirección a las manecillas del reloj; sin embargo, no se
indica en ninguna parte la ubicación de la fuente o de la carga. Una
vuelta completa (360 grados) representa una distancia correspondiente
a 0,5 , media vuelta (180 grados) corresponde a 0,25 y así
sucesivamente.
Existen dos casos particulares en éste análisis: el primero de ellos es
cuando se habla de una línea de transmisión que finaliza en circuito
abierto, en donde la impedancia es netamente resistiva e igual a
Infinito. Cuando ocurre ésta situación se representa en la carta sobre el
punto ( ,0 ) ubicado en el extremo derecho de la carta sobre el eje R tal
como se ilustra en la siguiente figura.
El segundo caso es cuando la longitud a recorrer es superior a 0,5 , en
cuyo caso de darán tantas vueltas cuanto sean necesarias teniendo en
cuenta que cada vuelta completa equivale a 0,5 .
Figura 94. Impedancia de una línea terminada en circuito abierto
El procedimiento para calcular la impedancia de entrada en una línea de
transmisión es el siguiente:
1. Calcular el valor de la impedancia z y graficarlo sobre la carta de
Smith.
2. Dibujar un círculo que pase por el punto z con centro en el punto
(1,0), el cual ilustra todos los valores de las impedancias que estarán
presentes sobre la línea de transmisión
3. Establecer un punto de referencia como punto de partida (A) para
calcular la impedancia basada en una distancia dada en longitudes de
onda. Éste punto se ubica sobre el círculo más externo de la carta en
donde se encuentran registradas las longitudes de onda, el cual deberá
ser en dirección normal al circulo dibujado perpendicular al punto z.
4. Girar en el sentido de las manecillas del reloj tantas longitudes de
onda como sean necesarias según la distancia establecida ubicando con
ello un punto A.
5. Trazar una recta que una el punto B con el punto (1,0) y el punto en
donde se corte el circulo dibujado según z con esta recta denominado C,
será el valor de la impedancia normalizada en entrada en la línea de
transmisión denominado z IN .
6. Calcular el valor real de la impedancia multiplicando el valor de la
impedancia z IN por la impedancia característica.
7. El punto donde el círculo dibujado se corte con el eje R, es el valor de
SWR (Punto D)
Ejemplo 1:
Determinar la impedancia de entrada de una línea de transmisión y su
valor de SWR ubicada a 1,25 de longitud, en donde Z L 30 j 40 , y la
impedancia característica Z O 50
Solución:
Primero se calcula la impedancia característica
z
ZL
ZO
30
j 40
50
0,6
j 0,8
Se traza el circulo con centro en (1,0) y luego la recta perpendicular al
punto z (Punto A) (Línea de color rosa).
A partir de ese punto se gira en sentido a las manecillas del reloj 1,25 ,
que corresponde a 2 vueltas completas y sobra 0,25 lo cual es lo que se
debe desplazar el punto después del punto A. Como el punto A está
ubicado a 0,12 con respecto al punto R=0. Entonces se puede decir que
0,25
0,37 con respecto al
la ubicación del punto B estará a 0,12
punto R=0 en la carta de Smith.
Luego se traza una línea desde el punto B hacia el punto (1,0) (línea
azul) y se ve que se corta con la circunferencia en el punto (0,63-j0,77)
el cual corresponde al punto C.
El punto D según la gráfica es el valor para SWR, que en éste caso es
SWR=2,9.
Finalmente, el valor de la impedancia de la línea de transmisión se
calcula multiplicando el valor de la impedancia obtenida en el punto C
por la impedancia característica:
Z IN
50 * (0,63
j 0,77 )
31,5
j 38,5
El resultado de éste proceso es el que se ilustra en la figura 95.
Figura 95. La carta de Smith para el ejemplo1
9.6.5 EJERCICIOS PROPUESTOS SOBRE ANTENAS Y GUÍAS DE ONDA
1. Una antena presenta las siguientes características: potencia de entrada 100
Wrms, amplitud de corriente 1.5 A y resistencia efectiva de 2 Ω. Calcular:
resistencia de radiación de la antena, potencia irradiada y eficiencia de la
antena.
2. Calcular la potencia isotrópica efectiva irradiada para una antena con
ganancia de potencia de 43 dB y una potencia irradiada de 200 W
3. Calcular la directividad de una antena en dB que produce una densidad de
potencia P = 2 µW/m2 en un punto en el que la antena de referencia
produce 0.2 µW/m2
4. calcular la potencia efectiva irradiada de una antena con directividad D =
350, una eficiencia de 0.65 y una potencia de entrada de 45 W
5. Calcular la eficiencia de una antena con resistencia de radiación de 20 Ω,
resistencia efectiva de 0.5 Ω y ganancia directiva de 150
6. Calcular la ganancia de potencia y la abertura de haz para una antena
helicoidal de radiación longitudinal con los siguientes parámetros: diámetro
de la hélice 0.12 m , numero de vueltas : 15 paso o separación entre
espiras: 0.03m y frecuencia de operación: 450 Mhz
7. Calcular la abertura del haz y las potencias de transmisión y recepción en
una antena parabólica con los siguientes parámetros: eficiencia del 55%,
frecuencia de operación: 3.5 GHz y diámetro del reflector 3 m
8. Una guía de onda rectangular con separación entre paredes de 3 cm y una
frecuencia de operación de 6 Ghz calcular: velocidad de fase, velocidad de
grupo, frecuencia de corte y longitud de onda de corte
9. En una antena con corriente rms de 4 A, una potencia de entrada de 350 W
y una resistencia de corriente continua de 4 Ω. calcular potencia irradiada
por la antena, eficiencia de la antena y resistencia de radiación.
10. Calcular la densidad de potencia en un punto a 15 km de una antena cuya
potencia de entrada es 35 W, directividad D= 16 dB y un eficiencia del 75 %
11. Calcular la densidad de potencia captura por una antena receptora con los
siguientes parámetros: potencia de entrada: 45W, ganancia de la antena de
transmisión: 30 dB, distancia entre antenas transmisor y receptora d = 25
km y ganancia directiva de la antena receptora 26dB
12. Calcular la ganancia de potencia en decibelios para una antena con
ganancia directiva D= 45 dB y una eficiencia del 70%
13. Calcular la potencia isotrópica efectiva irradiada para una antena con
ganancia de potencia de 30 dB y una potencia de radiación de 420 W
14. Calcular el valor de SWR y la impedancia de una línea de transmisión
ubicada a 0,25 de longitud, en donde Z L 10 j 20 , y la
impedancia característica Z O 50
15. Graficar la impedancia y la admitancia para los siguientes valores
de impedancia considerando una impedancia característica
Z O 55 :
Z L 15 j 20 , Z L j30 , Z L 40 , Z L 10 j 20
9.6.6 PREGUNTAS
1. Defina los siguientes conceptos: antena, campo eléctrico, campo
magnético, resistencia de radiación, eficiencia de una antena,
potencia irradiada isotrópica efectiva, polarización de una antena,
abertura del haz de una antena, antena no resonante, velocidad de
fase y velocidad de grupo.
2. Que es la directividad para una antena isotrópica
3. Cuales son las diferencias entre ganancia directiva y ganancia de
potencia
4. Haga un cuadro comparativo de los diferentes tipos de antenas
ilustrando sus principales características y sus aplicaciones
5. Describa brevemente que tipos de alimentación se utilizan
comúnmente en las antenas describiendo su funcionamiento
6. Describa brevemente algunos usos de la carta de Smith
BIBLIOGRAFÍA
TOMASI, Wayne. Sistemas de Comunicaciones Electrónicas. Prentice Hall, 4a Ed.
2003
CARDAMA, Angel. Antenas. AlfaOmega, 2da. Ed. 2003
HAYT, William. Teoría Electromagnética. McGraw-Hill. 2da Ed. 2000
BATALLER, Miguel. Líneas de Transmisión. Paraninfo. 2da. Ed. 1997
A.J. Giger, Low Angle Microwave Propagation: Physics and Modeling, Artech
House, Boston, 1991.
M.P.M. Hall, Effects of the Troposphere on Radio Communication, Peter
Peregrinus, Londres, 1979.
J.M. Hernando Rábanos, Transmisión por radio, Centro de Estudios Ramón
Areces, Madrid, 1993.
A. Ishimaru, Wave Propagation and Scattering in Random Media, Academic Press,
Nueva York, 1978.
A. Ishimaru, Electromagnetic Wave Propagation, Radiation and Scattering,
Prentice Hall, Englewood Cliffs, 1991.
W.C. Jakes, Microwave Mobile Communications, IEEE Press, Nueva York, 1974.
D.E. Kerr, Propagation of Short Radio Waves, M.I.T. Radiation Laboratory Series,
McGraw-Hill, Nueva York,1991,
J. Lavergnat, M. Sylvain, Radio Wave Propagation: Principles and Techniques,
John Wiley & Sons, Nueva York,
2000.
W.C.Y. Lee, Mobile Communications Engineering: Theory and Applications, 2.ª
ed., McGraw-Hill, Nueva York, 1998.