campos magnéticos inducidos y la corriente de

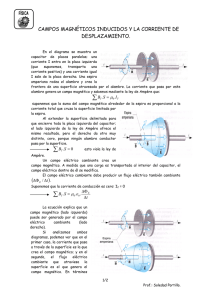
CAMPOS MAGNÉTICOS INDUCIDOS Y LA CORRIENTE DE
DESPLAZAMIENTO.
En el diagrama se muestra un
capacitor de placas paralelas; una
corriente I entra en la placa izquierda
(que
suponemos,
transporta
una
corriente positiva) y una corriente igual
I sale de la placa derecha. Una espira
amperiana rodea el alambre y crea la
frontera de una superficie atravesada por el alambre. La corriente que pasa por este
alambre genera un campo magnético y sabemos mediante la ley de Ampère que:
 B .S   .I
T
0
T
suponemos que la suma del campo magnético alrededor de la espira es proporcional a la
corriente total que cruza la superficie limitada por
la espira.
Al extender la superficie delimitada para
que encierre toda la placa izquierda del capacitor;
el lado izquierdo de la ley de Ampère ofrece el
mismo resultado, pero el derecho da otro muy
distinto, cero, porque ningún alambre conductor
pasa por la superficie.
 B .S  0
esto viola la ley de
T
Ampère.
Un campo eléctrico cambiante crea un
campo magnético. A medida que una carga es transportada al interior del capacitor, el
campo eléctrico dentro de él se modifica.
El campo eléctrico cambiante debe producir un flujo eléctrico también cambiante
 E / t  .
Suponemos que la corriente de conducción es cero: IC = 0
 B .S   .
T
0
0
.
 E
t
La ecuación explica que un
campo magnético (lado izquierdo)
puede ser generado por el campo
eléctrico
cambiante
(lado
derecho).
Si
analizamos
ambos
diagramas, podemos ver que en el
primer caso, la corriente que pasa
a través de la superficie es la que
crea el campo magnético; y en el
segundo,
el
flujo
eléctrico
cambiante que atraviesa la
superficie es el que genera el
campo magnético. En términos
1/4
Prof.: Soledad Portillo.
generales se deben explicar ambas formas de producir un campo magnético: a- una
corriente y b- con un flujo eléctrico cambiante.
Se modifica la ley de Ampère de forma tal que:
 B .S   .I   .
T
0
0
0
.
 E
t
La generalización de la ley de Ampère es obra de Maxwell.
Un campo magnético cambiante induce un campo
eléctrico (ley de Faraday), ahora vemos que un
campo eléctrico cambiante induce un campo
magnético.
En la figura se muestra como un campo magnético
inducido B, que es producido por el campo eléctrico
cambiante E.
2/4
Prof.: Soledad Portillo.
CORRIENTE DE DESPLAZAMIENTO.
En la generalización que realiza Maxwell sobre la ley de Ampère, vemos que el
término:
 0.
 E
tiene las dimensiones de una corriente; a pesar de que no hay
t
movimiento de cargas. A este término se le asigna el nombre de corriente de
desplazamiento.
ID   0.
 E
t
un campo magnético puede crearse mediante una corriente de
conducción IC o mediante una corriente de desplazamiento ID así obtenemos que:
 B .S   .I   .I
  B   I  I 
T
0
T
0
0
C
D
D
Si calculamos la corriente de desplazamiento I D en la separación del capacitor: la
carga q en las placas se relaciona con el campo eléctrico E en la separación por medio de
E
IC 

0
y entonces
q   0 .E. A (sabemos que   q
A
).
q  0 .E. A

t
t
La magnitud E. A es el flujo de campo eléctrico
podemos deducir que IC = ID e
I D   0.
 E
t
 E y, por lo tanto: I C   0 .
 E
t
concluimos que la corriente de desplazamiento en la
separación es igual a la corriente de conducción en
los alambres.
El concepto de corriente de desplazamiento
nos permite conservar la idea de que la corriente
es continua.
Una corriente de conducción ID entra el la
placa positiva y sale de la placa negativa. La
corriente de conducción no es continua en la
separación del capacitor, porque no se transporta
carga alguna a través de esta separación. No obstante, allí la corriente de desplazamiento
ID es exactamente igual a IC; con esto se mantiene el concepto de continuidad de la
corriente.
Cuando el capacitor está cargado por completo, la corriente de conducción
desciende súbitamente a cero (no fluye corriente en los alambres). El campo eléctrico
entre las placas se vuelve constante, por lo mismo la corriente de desplazamiento también
se reduce a cero.
3/4
Prof.: Soledad Portillo.
ECUACIONES DE MAXWELL.
Las ecuaciones de Maxwell no son meras especulaciones teóricas; cada una de ellas
fue formulada para explicar los resultados de experimentos obtenidos en laboratorios.
En la siguiente tabla se sinterizan las ecuaciones y los experimentos decisivos que
dio origen a cada una de ellas.
ILey de Gauss para la electricidad.
E.S 
E 
qneta
a- Cargas iguales se repelen y cargas diferentes se
atraen como el cuadrado del inverso de la separación.
0
qneta
b- Una carga en un conductor aislado se dirige a la
superficie exterior.
0
II-
Ley de Gauss para el magnetismo.
B.S  0
B  0
III-
Las líneas del campo magnético forman espiras cerrada; no
hay evidencia de que existan monopolos magnéticos.
Ley de inducción de Faraday.
 B
t
 B

t
Un imán de barra, introducido en una espira cerrada de
alambre, creará una corriente en está última.
E.S  
Eind
IV-
Ley de Ampère – Maxwell:
BT .S   0 .I C   0 . 0 .
BT .S   0 .I C   0 .I D
 E
t
 E 

E B  0  I C   0 .

t 

a- Una corriente en un alambre produce un campo
magnético cerca de él.
b- La velocidad de la luz se calcula exclusivamente con
mediciones electromagnéticas.
A partir de ellas se puede examinar:
1- Simetría: La inclusión de la corriente de desplazamiento ocasiona que las ecuaciones
III y IV se asemejen más, mejorando con ello su simetría. Si se confirmase la
existencia de los monopolos, las ecuaciones parecerían más similares.
2- Ondas electromagnéticas: las cuatro ecuaciones se conocían ya antes de la época de
Maxwell. Cuando se combinan estas ecuaciones surge otra predicción, la existencia de
ondas electromagnéticas y un valor de su velocidad (la velocidad de la luz). Estas ondas
fueron predichas por Maxwell y descubiertas por Heinrich Hertz en 1888, quince años
después de publicarse la teoría de Maxwell.
3- Electromagnetismo y relatividad: las ecuaciones de Maxwell son notables porque son
enteramente compatibles con la teoría especial de la relatividad; las ecuaciones no
cambian para ningún observador, cualquiera que sea su velocidad relativa. El
descubrimiento de Einstein de la relatividad se basó directamente en la interpretación
que éste dio a las leyes del electromagnetismo y a las ecuaciones de Maxwell.
4/4
Prof.: Soledad Portillo.