PRÁCTICA 1
Anuncio

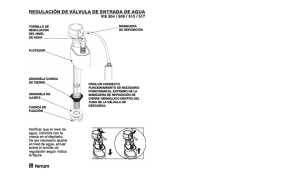
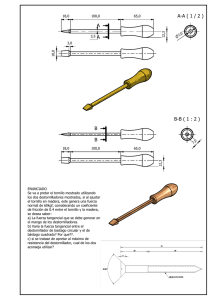
Fundamentos Físicos de la Ingeniería Ingeniería Industrial Prácticas de Laboratorio PRÁCTICA 1 Medidas geométricas. Errores de medida 1.1 Objetivos Aprender a utilizar 3 instrumentos básicos de medida de magnitudes geométricas: calibre (o pie de rey), tornillo micrométrico (o palmer) y esferómetro. Caracterizarlos por su sensibilidad y error de cero. Obtener medidas directas e indirectas con sus correspondientes errores. 1.2 Fundamento teórico 1.2.1 Calibre (o pie de rey) Es un instrumento utilizado para la medida de distancias, profundidades y separación entre partes de piezas. Consta de una escala lineal, a lo largo del eje del instrumento, sobre la que se desliza una cabeza graduada que define, entre las partes biseladas, la zona de medida. En esta cabeza móvil se encuentra situada una segunda escala, denominada nonius, que permite medir fracciones de la mínima unidad de medida de la escala principal. Ambas escalas pueden venir etiquetadas en Sistema Internacional, en milímetros, y en otras unidades como pulgadas y sus divisiones. Evidentemente, deben utilizarse únicamente las escalas en Sistema Internacional. El calibre suele incorporar un dispositivo de fijación (tornillo o mordaza) que inmoviliza la cabeza de medida una vez que se ha situado correctamente respecto a la pieza/distancia que se desea medir. Esta sujeción debe manejarse con especial atención y, en ningún caso, debe forzarse. 1 Fundamentos Físicos de la Ingeniería Ingeniería Industrial Prácticas de Laboratorio Para realizar una medida, una vez fijada la cabeza de lectura, buscamos los valores de la escala principal (longitudinal) entre los que se encuentra el cero de la escala secundaria (nonius). Esta posición nos indica las unidades de la escala principal, habitualmente milímetros. Las fracciones de esta unidad se leen a continuación observando la primera división (marca) del nonius que coincide exactamente con una división (marca) de la escala principal. 1.2.2 Tornillo micrométrico (o palmer) Es un instrumento utilizado para medir espesores de piezas. Consta de una mordaza con un vástago desplazable mediante un mecanismo de tornillo con dos escalas de medida: una escala longitudinal a lo largo del eje del tornillo y una escala circular alrededor del mismo. Cuando se gira una/dos vueltas el tornillo, avanza una unidad a lo largo de la escala longitudinal. Ésta suele estar graduada en milímetros mientras que la escala circular puede venir numerada de 1 a 50 o de 1 a 100, con un número variable de divisiones intermedias. Cuando la escala circular corresponde a un avance de media unidad de la escala longitudinal, en ésta suele incorporarse una marca intermedia que nos indica si, entre dos divisiones de la misma, nos encontramos en la primera o en la segunda vuelta de avance. La zona de medida está definida por dos superficies planas paralelas por lo que resulta especialmente adecuada para medir espesores, si bien debe tenerse especial cuidado en no apretar excesivamente el tornillo para no deformar el objeto a medir ni el mecanismo de apriete. 1.2.3 Esferómetro Es un instrumento utilizado para medir el radio de curvatura de una superficie. Consta de un trípode soporte, cuyas puntas de apoyo definen un triángulo equilátero de lado d, y un vástago central que se desplaza mediante un 2 Fundamentos Físicos de la Ingeniería Ingeniería Industrial Prácticas de Laboratorio mecanismo de tornillo (dotado de escalas longitudinal y circular, análogas a las del tornillo micrométrico). Puede demostrarse que, estando las tres patas en contacto con la superficie cuyo radio de curvatura se desea medir, cuando el vástago central está también en contacto con la superficie, la altura h que la punta central alcanza respecto al plano definido por las puntas de las otras 3 patas se relaciona con el radio de curvatura de la superficie por R= d 2 + 3h 2 6h 1.3 Montaje experimental El montaje experimental consta de los 3 instrumentos de medida (calibre, tornillo micrométrico y esferómetro) y de 4 piezas: paralelepípedo de madera, cilindro metálico, placa metálica y pieza esférica de vidrio. 1.4 Resultados que deben obtenerse Para cada uno de los 4 cuerpos (cilindro metálico, paralelepípedo de madera, placa metálica y casquete esférico de vidrio, deben tomarse las siguientes medidas (seleccionando los instrumentos adecuados, y corrigiendo las medidas con el error de cero, si existe) 1.4.1 Paralelepípedo de madera Mídase 3 veces cada uno de los 3 lados y calcúlense los valores medios. A partir de éstos, calcúlese –con su error- el volumen de la pieza, indicándose las expresiones utilizadas. 3 Fundamentos Físicos de la Ingeniería Ingeniería Industrial Prácticas de Laboratorio L11(mm) L12(mm) L13(mm) L1 (mm) L21(mm) L22(mm) L23(mm) L2 (mm) L31(mm) L32(mm) L33(mm) L3 (mm) Lado 1 medido Lado 1 corregido (con error de cero) Lado 2 medido Lado 2 corregido (con error de cero) Lado 3 medido Lado 3 corregido (con error de cero) Instrumento utilizado: _________________________ Sensibilidad: ___________ mm Error de cero: ___________ mm Expresiones: V= Ev = Valores: V ± EV = ____________________ mm3 4 Fundamentos Físicos de la Ingeniería Ingeniería Industrial Prácticas de Laboratorio 1.4.2 Placa metálica Mídase en 10 posiciones el espesor e de la misma. Calcúlense el valor medio, desviación estándar y el error de la medida. e1(mm) e2(mm) e3(mm) e4(mm) e5(mm) e6(mm) e7(mm) e8(mm) e9(mm) e10(mm) Espesor medido Espesor corregido (con error de cero) Espesor medido Espesor corregido (con error de cero) Instrumento utilizado: _________________________ Sensibilidad: ___________ mm Error de cero: ___________ mm e = ________ se = ________ Ee = ________ 1.4.3 Cilindro metálico: mídanse 3 veces la altura y el diámetro y calcúlense los valores medios. h1(mm) h2(mm) h3(mm) h (mm) Altura medida Altura corregida (con error de cero) Instrumento utilizado: _________________________ Sensibilidad: ___________ mm Error de cero: ___________ mm 5 Fundamentos Físicos de la Ingeniería Ingeniería Industrial Prácticas de Laboratorio d1(mm) d2(mm) d3(mm) d (mm) Diámetro medido Diámetro corregido (con error de cero) Instrumento utilizado: _________________________ Sensibilidad: ___________ mm Error de cero: ___________ mm 1.4.3.i) A partir de los valores medios, calcúlese el volumen del cilindro. Escríbase la expresión del error y calcúlese su valor numérico. Expresiones: V= EV = V±EV = __________________ mm3 Valores: 1.4.3.ii) Suponga que, por otro procedimiento, se ha calculado el volumen para un conjunto de 5 cilindros de igual radio Ro = 10.07 ± 0.03 mm y diferentes alturas h, obteniéndose los valores que se indican a continuación. V (mm3) 3160 6300 9399 12530 15723 h (mm) 10 20 30 40 50 6 Fundamentos Físicos de la Ingeniería Ingeniería Industrial Prácticas de Laboratorio Represente gráficamente V frente a h y calcule y trace la recta de mejor ajuste (pendiente a, ordenada en el origen, b, –con sus errores y unidades- y coeficiente de correlación lineal, ro). a±Ea = ________ b±Eb = ________ A partir de la pendiente, calcule el valor numérico de ro = ________ π con su error, indicando las expresiones utilizadas: Expresiones: π= Eπ = π ± Eπ Valores: = __________________ 1.4.4 Pieza esférica de vidrio Para caracterizar el esferómetro, mídase la distancia d entre las 3 puntas de apoyo y obténgase su valor medio (considerado sin error). d1(mm) d2(mm) d3(mm) d (mm) Distancia 7 Fundamentos Físicos de la Ingeniería Ingeniería Industrial Prácticas de Laboratorio Para conocer el radio de curvatura de la pieza, mídase en 2 posiciones la distancia h de la punta central al plano definido por los extremos de las 3 puntas de apoyo, corrigiéndolo con el error de cero h1(mm) h2(mm) h (mm) Altura medida Altura corregida (con error de cero) Sensibilidad: ___________ mm Error de cero: ___________ mm A partir de los valores medios obtenidos, calcúlese –con su error- el valor del radio de curvatura de la pieza. Indíquense las expresiones utilizadas. Expresiones: R= ER = Valores: R ± ER = __________________ mm 8