Resumen: teoría de juegos y estrategia competitiva I Ideas clave
Anuncio

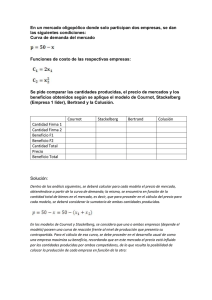
Resumen: teoría de juegos y estrategia competitiva I Cifras reducidas y comportamiento estratégico • Diversión y juegos con un ejemplo de dupolio – – – – Elección simultánea frente a secuencial Juego de una sola vez frente a juego repetido Cantidad frente a precio como la variable de elección Bien homogéneo frente a diferenciado • Repaso de la analítica Ideas clave • Conocer la situación estratégica (¿cuál es el juego?). • ¡Su competidor es tan listo como usted! • Piense en la respuesta de los demás • Equilibrio de Nash: todos los participantes hacen lo que pueden, dado el comportamiento de los competidores El juego (a) • • • • • Objetivo: Maximizar su beneficio Nº de juegos: 1 sólo Bien: Homogéneo Variable de elección: Cantidad Momento de la elección: Simultáneo Matriz de pagos Firma 2 (competidora) 15 Firma 1 (usted) 15 20 20 Matriz de pagos Firma 2 (competidora) 15 20 22,5 30 15 450, 450 375, 500 338, 506 225, 450 Firma 1 20 (usted) 500, 375 400, 400 350, 394 200, 300 22,5 506, 338 394, 350 338, 338 125, 150 30 450, 225 300, 200 150, 125 0, 0 El juego (a*) • • • • • Objetivo: Nº de juegos: Bien: Variable de elección: Momento de la elección: Maximizar su beneficio 2 Homogéneo Cantidad Simultáneo El juego (a**) • • • • • Objetivo: Nº de juegos: Bien: Variable de elección: Momento de la elección: Maximizar su beneficio 10 Homogéneo Cantidad Simultáneo Analítica: juego simultáneo de Cournot • Bien homogéneo, elección simultánea • Elección de cantidad, Q • Objetivo: Maximizar su beneficio • Demanda del mercado: P = 60 - Q • Producción: Q = Q1 + Q2 CM1 = CM2 = 0 ¿Cuál es la curva de reacción de la firma? (Firma 1 ejemplo) • Para el máximo beneficio, IM = CM R1 = PQ1 = (60 - Q)Q1 = 60Q1 - (Q1 + Q2)Q1 = 60Q1 - (Q1)2 - Q2Q1 IM 1 = dR1/dQ1 = 60 - 2Q1 - Q2 Disponga que IM1 = CM = 0, lo que arroja Q1 = 30 - ½ Q2 (curva de reacción de la firma 1) Equilibrio de Cournot • Curvas de reacción simétricas: (Firma 1) Q1 = 30 - 1/2 Q2 Q2 = 30 - 1/2 Q1 (Firma 2) • Equilibrio: Q 1 = Q2 = 20 • Cantidad total: Q = Q1 + Q2 = 40 • Precio: P = 60 - Q = 20 • Beneficios: Π 1 = Π2 = 20·20 = 400 Duopolio: versión gráfica Q2 60 Curva de reacción de la firma 1 Equilibrio de Cournot 30 20 15 Resultados colusivos Curva de reacción de la firma 1 15 20 30 60 Q1 Analítica del duopolio - Colusión Demanda: P = 60 – Q Π = P · Q - Costes = (60 - Q)·Q dΠ = 60 − 2Q = 0 dQ ⇒ Q = Q1 + Q2 = 30, P = 30 Total conjunto Π = 30(30) = 900 Si se divide por igual, Π1 = Π2 = 450 El juego (b) • • • • • Objetivo: Nº de juegos: Bien: Variable de elección: Momento de elección: Maximizar su beneficio 1 Homogéneo Q alguien va primero Matriz de pagos Firma 2 (competidora) 15 20 15 450, 450 375, 500 338, 506 225, 450 Firma 1 20 (usted) 500, 375 400, 400 350, 394 200, 300 22,5 506, 338 394, 350 338, 338 125, 150 30 300, 200 150, 125 0, 0 450, 225 22,5 30 Analítica de la primera intervención (La variable de decisión es Q) • Suponga que la Firma 1 actúa primero • Para establecer el resultado, la Firma 1 debe considerar como responderá la Firma 2 • Sabemos como responderá la Firma 2. Seguirá su curva de reacción de Cournot: Q2 = 30 - 1/2 Q1 • Por tanto, la Firma 1 maximizará su resultado teniendo en cuenta esta información Primera intervención: máximo Π dada la reacción del seguidor • Ingresos de la Firma 1: R1 = Q1P = Q1(60 - [Q1 + Q2]) = 60Q1 - (Q1)2 - Q1Q2 = 60Q1 - (Q1) 2 - Q1 (30 - ½ Q1) = 30Q1 - ½ (Q1)2 Reacción de la firma 1 • Ingreso marginal de la firma 1: IM 1 = dR1/dQ1 = 30 - Q1 Primera intervención - Resultado • Ingreso marginal de la Firma 1: IM 1 = 30 - Q1 • Determine IM1 = CM (= 0), y Q1 = 30 Q2 = 30 - ½ Q1 = 15 • Precio: P = 60 - (Q1 + Q2) = 15 • Beneficios: Π 1 = 30 ·15 = 450 Π2 = 15 ·15 = 225 El juego (c) • • • • • Objetivo: Maximizar su beneficio Nº de juegos: 1 Bien: Homogéneo Variable de elección: Precio Momento de la elección: Simultáneo Sustitutos estratégicos frente a complementos • Complemento estratégico: reacciones coincidentes – p.ej. precios bajos como reacción a la bajada de precios del competidor • Sustituto estratégico: reacciones encontradas – p.ej. reducción en la cantidad como reacción a la mayor cantidad del competidor • La competencia tiende a ser más agresiva con complementos estratégicos que con sustitutos El juego (c*) • Objetivo: Maximizar su beneficio • Nº de juegos: 1 • Bien: Diferenciado • Variable de elección: Precio • Momento de la elección: Simultáneo Cuestiones para recordar • La teoría de juegos permite el análisis de situaciones en las que existe interdependencia • Equilibrio de Nash : cada jugador actúa de la mejor manera posible, considerando lo que hace el otro • La competencia en complementos estratégicos (precio) tiende a ser más dura que en sustitutos (cantidad) • El compromiso es importante, ya que las reglas del juego las hace usted. Puede dar lugar a que el jugador que intervenga primero tenga ventaja • La repetición conduce a la cooperación, pero sólo cuando el juego final es incierto o está lejos Preparación para la próxima clase El caso práctico “Lesser Antilles Lines”: • Buen caso para desarrollar análisis de juegos y de pagos (suposiciones, beneficios, etc.). • NO es necesario que lo prepare para la clase (parte del boletín de problemas 5).