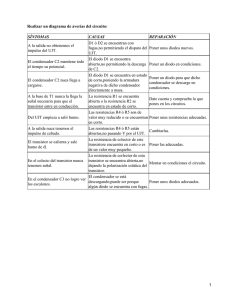
k xLn xx fCLn R x x x R T C CR CR Ln T RCLn f T 36 36378 6.01 1

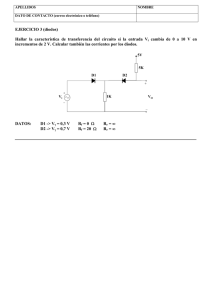
Examen de Electrónica Industrial.
1 de septiembre de 2006
Tiempo: 2:30 horas.
Problema 1 (1 punto)
En la figura 1 se muestra un circuito de disparo de tiristores usando un UJT. La tensión de
alimentación del circuito es Vs = 30V. Los parámetros del UJT son:
Relación de separación intrínseca µ = 0.6
Tensión del diodo interno del UJT Vd = 0.5V
Tensión y corriente de valle Vv = 4V, Iv = 13mA.
RB2 = 550 ohm
Corriente de pico Ip = 20m.
RB1=100 ohm
figura 1
Explicar el funcionamiento del circuito y escoger R y C para que la frecuencia de disparo del tiristor
sea aproximadamente de 120Hz y el ancho del pulso de disparo o tiempo de descarga del
condensador sea aproximadamente T2 = 50µs (tiempo transcurrido desde el valor máximo de
tensión en el condensador hasta que esta cae a 0.1 veces su tensión máxima).
Solución:
De las ecuaciones:
1
1
= RCLn
f
1− µ
T2 = − Ln0,1RB1C ≈ 2 RB1C
T=
T2
50 x10 −6
C≈
=
= 2.5 x10 −7
2 RB1
2 x100
R=
1
fCLn
1
1− µ
=
1
120 x 2.5 x10 −7 xLn
1
1 − 0 .6
Sabemos que para que conduzca el diodo, mínimo
= 36378 ≈ 36k
entonces
por otra lado
Con estas relaciones sabemos que el valor de R debe estar:
2Kohm <R<575kohm
Problema 2 (1 punto)
Se conectan dos diodos de 1800 V en serie para soportar una tensión de 2.7 kV. La pendiente de la curva
característica cuando el diodo está en corte es de 15 µA/V y 10 µA/V para cada uno de los diodos
respectivamente.
a)
b)
Determinar como se reparte la tensión entre los dos diodos (0.25 puntos).
Seleccionar el valor de las resistencias que se deben colocar en paralelo con los tiristores
(idéntico para los dos tiristores), de manera que la tensión máxima en cualquiera de ellos no
supere los 1500 V. (0.5 punto).
Calcular la potencia disipada en las dos resistencias del apartado b) (0.25 puntos).
c)
Solución:
a)
La resistencia equivalente de los diodos en corte es:
R1 = 1/15 µA/V = 67 Kohm
R2 = 1/10 µA/V = 100 Kohm
Los dos diodos en serie equivalen a un divisor de tensión resistivo, y las tensiones en cada uno
serán:
V1 = 2700V x R1/(R1+R2) = 1083V
b)
V2 = 2700V x R2/(R1+R2) = 1617V
Para ecualizar la tensión de los diodos se coloca en paralelo con ellos dos resistencias de
idéntico valor R.
V1+V2 = 2700 de hecho V1 = 1200, V2 = 1500 y
Despejando R = 103 k
c)
Las potencias serán
V1/(R1|| R) = V2 / (R2||R)
2
P1= (V1) /R =1200 x 1200 / 103000 = 14W
y
2
P2= (V2) /R =1500 x 1500 / 103000 = 21,8 W
Problema 3 (1 punto)
Tras medir la corriente de entrada de un rectificador AC-DC monofásico con una tensión de entrada
sinusoidal se ha obtenido la siguiente tabla de armónicos.
Nº armónico
3
5
7
9
11
13
15
17
19
21
23
37
7.5
2.1
2.1
1.8
1.5
1.01
0.93
0.90
0.63
0.5
La corriente no tiene componente continua y su componente fundamental (I1) se halla en fase
respecto a la tensión de entrada. Determine el factor de potencia (PF) y la distorsión armónica total
(THD) en los siguientes dos casos:
-Hasta el armónico de orden 23
-Hasta el armónico de orden 13
Calcule el porcentaje de error entra ambas mediciones.
Solución
∞
∑I
THD =
2
n
n=2
I1
I
= ∑  n
n = 2  I1
∞



2
PF =
1
I
1 + ∑  n
n= 2  I 1
∞




2
=
1
1 + THD 2
Problema 4 (2 puntos)
En un rectificador monofásico de media onda, se dispone de una batería de carga con capacidad de
100W-h y tensión E = 12V. La corriente media es Idc=5A. La tensión eficaz de entrada es Vp = 60V,
50Hz. Calcular:
A) Intervalo de conducción del diodo
B) Valor de la resistencia limitadora de corriente (R).
C) Valor de la potencia disipada en R.
D) El tiempo de carga de la batería (T) expresado en horas.
E) La eficiencia del rectificador.
F) La tensión inversa de pico en el diodo (PIV)
figura 2
Solución
a) 163.74º; b) 4.26W; c) 286.4W); d) 1.667h; e) 17.32%; f) 96.85V.
a) El diodo comienza a conducir cuando la tensión de entrada supera la tensión de la batería y deja
de conducir cuando se hace menor que la tensión de la batería, de manera que el intervalo de
conducción del diodo vale d = w t2-w t1 :
d = wt2-wt1=163,74°
b) La corriente media de carga la calcularemos mediante la expresión:
de donde obtenemos que:
c) La corriente eficaz en la batería será:
d) Calculamos ahora la potencia PDC entregada a la batería:
la capacidad de la batería es de 100 W-h de manera que el tiempo de carga de la misma en horas es
e) El rendimiento o eficiencia del rectificador valdrá:
f) La tensión inversa de pico en el diodo será:
Problema 5 (1.5 puntos)
Un convertidor DC-DC elevador (Boost) proporciona una tensión de salida constante (Vo = 24 V ) a
partir de una tensión de entrada (Vi) variable entre 12V y 20V. El convertidor opera a una frecuencia
de 100 kHz y el condensador de salida es de 1 mF. La corriente de carga mínima es de 2 A y la
máxima de 5A. Obtener:
a)
b)
c)
El valor mínimo de la inductancia del circuito para que este opere en régimen de conducción
continua (CCM) con una tensión de entrada de 16 V en todo el rango de corrientes.
Con el valor de la inductancia calculado previamente obtener el valor máximo de la corriente
media por el diodo dentro del rango de operación descrito.
Obtener el rizado de la tensión de salida en función de la tensión de entrada (Vi) y de la corriente
de salida. Nota: El convertidor opera siempre en régimen de conducción continua.
Solución
a)
El límite entre CCM y DCM se obtiene con la mínima corriente de salida, I o= 2A.
Para obtener una tensión de salida de 24V con 16V de salida en régimen continuo o en el límite
con el régimen discontinuo ( Vo = Vi/(1-D) ) el ciclo de trabajo es D = 1 – Vi/Vo = 0.333
Po=Pi ---- Vo x Io = Vi x Ii -------- (teniendo en cuenta que la corriente de entrada es igual a la
corriente de la bobina ------------ IL=Ii = Vo x Io / Vi = 24 x 2 / 16 = 3A.
El rizado de la corriente en la bobina es ∆ IL = VL x D x T/ L = VI x D x T/ L
En el límite entre CCM y DCM IL = ∆ IL / 2 -------------- ∆ IL = 6A
Lmin = VI x D x T / ∆ IL = VI x D / ( f x∆ IL) = 16 x 0.333 / (100000 x 6) = 8.9 µH.
b)
El valor medio de la corriente por el diodo es igual a la corriente de carga (Valor medio de la
corriente por el condensador = 0), por lo tanto
IDmax = 5A.
c)
Del dibujo de la corriente en el condensador (Ic(t) = Id(t) –Io(t))
El
Ic
ILmax-Io
ILmin-Io
+
t
DT
1-DT
-Io
El rizado de la tensión es
∆ Vo_pico-pico = area (+)/C = area (-) / C = Io x D x T/ C = Io x (1 – Vi/Vo )/ (f x C)
El rizado es independiente de L y se obtiene el valor máximo para Iomax y Vimin.
∆ Vo_pico-picomax=5 x ( 1-12/24)/(100000 x 0.001) = 25 mV
Problema 6 (1.5 puntos)
El circuito de la figura es un inversor monofásico. Si la carga es de tipo RC (en serie),
suponiendo que opera en régimen permanente y el período es T = 4RC. Obtener:
a)
b)
Expresión de la corriente por la carga
Intervalo de conducción de los IGBT-s y los diodos.
figura 3
Solución
a)
En el semiciclo positivo
Vin = Ri (t ) +
−t
di (t ) 1
1 t
+ i (t )
i (t )dt + Vc (0) ------- derivando 0 = R
∫
0
C
dt
C
[
i (t ) = Ae τ ∈ 0, T
2
]
con
τ = RC
Sustituyendo en la ecuación inicial en el semiciclo positivo , teniendo en cuenta que T = 4RC :
1 0
i (t )dt + Vc (0) = RA + Vc (0) → Vc (0) = Vin − RA
C ∫0
1 T /2
Vin = Ri (T ) + ∫ i (t )dt + Vc (0) = RAe − 4 RC / 2 RC + Vc (T ) → Vc (T ) = Vin − RAe − 2
2 C 0
2
2
Vin = Ri (0) +
Debido a la simetría de la onda en el semiciclo negativo
− t +T / 2
i (t ) = Be
τ
[
∈ T ,T
2
]
Vc (T / 2) = −Vc (0) A =
, B = -A y
[
De manera que
]
 I e − t τ ∈ 0, T
 0
2
i (t ) = 
t −T / 2
−
− I 0 e τ ∈ T , T

2
[
]
donde I 0 =
2Vin
= I0
R 1 − e −2
(
2Vin
R 1 − e −2
(
)
)
b) En este caso solo conducen los transistores, en el semiciclo positivo T1 y T2 y en
el negativo T3 y T4, ya que la corriente mantiene el signo en cada uno de los
intervalos.