Segunda prueba de control resuelta y comentada

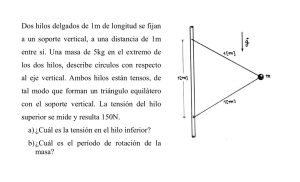
Departamento de Física Aplicada III
Escuela Superior de Ingenieros
Camino de los Descubrimientos s/n
41092 Sevilla
Fı́sica II
Segunda Prueba de Control
Grado en Ingenierı́a de Tecnologı́as Industriales. Primer Curso.
Mayo de 2011
APELLIDOS:
NOMBRE:
Este test se recogerá una hora y media después de ser repartido.
El test se calificará sobre 10 puntos, repartidos equitativamente entre todas las preguntas.
Las respuestas erróneas restarán 1/3 de la puntuación de una correcta. Las respuestas en blanco
no contribuyen a la nota del test. Caso de que la nota total resulte negativa, la puntuación final
será cero.
En cada pregunta, solo una de las respuestas es correcta. Marque la respuesta correcta con
×). Si desea modificar una respuesta, tache la ya escrita (2 ) y escriba una cruz sobre
un aspa (2
la nueva.
T.1 La figura adjunta muestra un hilo de corriente muy largo que pasa por la arista de un cubo
imaginario de lado d. Indique qué relación es válida para el módulo del campo magnético
creado por el hilo en los puntos de los vértices del cubo que se indican en la figura.
2 A.
2 B.
× C.
2
2 D.
B1 = B2 = B3 = B4 .
B1 = B2 > B3 > B4 .
B1 = B2 = B3 > B4 .
B1 > B2 > B3 > B4 .
El módulo del campo magnético del hilo decrece con la inversa de la distancia al hilo. Los
puntos 1,2 y 3 están
√ a la misma distancia (d) del hilo mientras que el punto 4 está a una
distancia mayor ( 2d).
T.2 Sea una espira plana de corriente situada en una región donde existe un cierto campo
magnético externo. Debido a la acción de este campo magnético externo la espira en
general...
× A.
2
2 B.
2 C.
2 D.
podrı́a rotar y desplazarse.
podrı́a rotar, pero no se desplaza en ningun caso.
no rota ni se desplaza a no ser que esté fabricada con un material ferromagnético.
podrı́a desplazarse, pero no rotar.
En general puede aparecer un momento de rotación y también una fuerza neta sobre la
espira que puede hacer que se desplace. La fuerza neta es nula solamente si el campo es
uniforme.
T.3 Se dispone en el laboratorio de una bobina o solenoide de 1000 vueltas y 50 cm de longitud
(solenoide A) y de otro de 3000 vueltas y 60 cm de longitud (solenoide B). Se hace pasar
una corriente de 100 mA por el solenoide A y se obtiene un valor determinado del campo
magnético en su interior. ¿Qué corriente es preciso hacer pasar por el solenoide B para
obtener en su interior el mismo valor del campo magnético?
2 A.
× B.
2
2 C.
2 D.
250 mA.
40 mA.
33,3 mA.
120 mA.
El campo en el interior de un solenoide es B = µ0 nI. El primer solenoide tiene una densidad
de bobinado nA = 1000/50 = 20 vueltas/cm y el segundo nB = 3000/60 = 50 vueltas/cm.
Si ambos dan el mismo valor del campo tenemos: µ0 nA IA = µ0 nB IB , de donde: IB =
nA IA /nB = 2IA /5 = 40 mA.
T.4 La figura muestra tres hilos conductores muy largos que transportan las corrientes que se
muestran. ¿Qué sentido tiene la resultante de la fuerza que los hilos 1 y 3 ejercen sobre el
hilo 2?
2 A.
2 B.
× C.
2
2 D.
Es una fuerza dirigida hacia el hilo 1.
Es una fuerza dirigida hacia el hilo 3.
Es una fuerza nula.
No puede determinarse con los datos que se suministran.
Las fuerza entre dos corrientes paralelas es atractiva. Por tanto ambos hilos (1 y 3) atraen
al hilo 2. Es decir, ejercen fuerzas paralelas y de sentidos contrarios. El módulo de la
fuerza por unidad de longitud entre corrientes paralelas es proporcional al producto de las
intensidades e inversamente proporcional a la distancia entre los hilos (F ∝ I1 I2 /d). Para
los hilos 1 y 2 I1 I2 = 6 A2 mientras que para 3 y 2 I2 I3 = 12 A2 . Sin embargo se observa
en el dibujo que la distancia entre los hilos 2 y 3 es el doble que la distancia entre 1 y 2.
En consecuencia el producto de las intensidades partido por la distancia entre hilos sale
idéntico para ambas parejas de hilos. Eso significa que las fuerzas son iguales y de sentidos
contrarios y entonces la resultante es nula.
T.5 Un hilo recto que transporta una corriente I atraviesa una región donde existe un campo
magnético uniforme y perpendicular al hilo, tal como se muestra en la figura. El campo
tiene un módulo B y ejerce sobre el hilo una fuerza de módulo F . ¿Qué modificación
habrı́a que hacer en este sistema para que la fuerza sobre el hilo vea doblado su módulo
(es decir, sea 2F ) y apunte hacia arriba (eje y)?
× A.
2
2 B.
2 C.
Doblar el valor de la intensidad que recorre el hilo.
2 D.
Doblar el valor de la intensidad que recorre el hilo e invertir su sentido.
Doblar el módulo del campo magnético e invertir el sentido de la corriente.
Ninguna de las modificaciones propuestas permite obtener una fuerza con esa dirección y sentido.
La fuerza sobre un hilo recto de corriente debida a un campo magnético uniforme es
⃗ × B,
⃗ que en este caso apunta hacia arriba. Lo único que hace falta para obtener el
F⃗ = I L
resultado que se pide es doblar el módulo de la fuerza, lo que se puede lograr multiplicando
la intensidad en el hilo por 2.
Fı́sica II - Segunda Prueba de Control
Mayo de 2011
APELLIDOS:
NOMBRE:
T.6 En la figura se muestran tres situaciones de movimiento relativo entre una barra imantada
y un anillo conductor. Se representa también la corriente inducida en el anillo en cada
caso. ¿Para cuál de los tres casos el sentido de la corriente que se representa es incorrecto?
2 A.
2 B.
2 C.
× D.
2
Para el caso 1.
Para el caso 2.
Para el caso 3.
Los tres son correctos.
Aplicación directa de la Ley de Lenz. Alternativamente, es posible razonar pensando que
el anillo en cada caso debe comportarse como un momento magnético (imán) orientado de
tal forma que la fuerza entre la barra imantada y el anillo se oponga al movimiento.
T.7 Una baterı́a de 9 voltios está conectada a una bobina (devanado primario) tal como muestra
la figura adjunta. En el instante t = 0 se abre el interruptor presente en el circuito. ¿En
qué momento es posible medir una diferencia de potencial V2 a la salida del devanado
secundario?
2 A.
2 B.
× C.
2
2 D.
En cualquier instante de tiempo antes de t = 0.
En cualquier instante de tiempo a partir de t = 0.
Durante un lapso de tiempo inmediatamente después de t = 0.
En ningún momento.
Según la Ley de Faraday la fem inducida en el devanado secundario aparece cuando lo
atraviesa un campo magnético variable en el tiempo. Esto solamente ocurre en un
breve intervalo de tiempo desde que se abre el interruptor, en el cual el campo magnético
está pasando de un valor inicial constante a cero.
T.8 Una espira circular cerrada con una bombilla (equivale a una resistencia) se sitúa en un
plano en el que hay un cable conductor muy largo que transporta una corriente variable
I. La grafica muestra la variación de I con el tiempo. ¿En cuál de los instantes de tiempo
representados brillará con más intensidad la bombilla?
2 A.
2 B.
× C.
2
2 D.
En t1 .
En t2 .
En t3 .
No brilla en ningún caso.
A mayor fem inducida en la espira mayor será el brillo de la bombilla (P = ε2 /R). Según
la Ley de Faraday la fem es proporcional a la rapidez con la que el flujo magnético que
atraviesa la espira cambia con el tiempo. Calcular el flujo magnético en este caso no es
fácil, pero no hace falta: como el campo magnético creado por el hilo es directamente
proporcional a su intensidad, el flujo magnético también lo es y de ahı́ se deduce que la
fem es proporcional a dI/dt, es decir, a la pendiente de la curva I(t). En la gráfica se
observa a simple vista que el punto de mayor pendiente es el que corresponde a t3 .
T.9 En termodinámica un sistema cerrado se define como aquel que...
2 A.
× B.
2
2 C.
2 D.
no intercambia masa ni energı́a con el entorno.
no intercambia masa con el entorno, pero sı́ energı́a.
no intercambia energı́a con el entorno, pero sı́ masa.
posee una frontera conocida.
T.10 El Principo Cero de la Termodinámica permite...
2 A.
2 B.
× C.
2
2 D.
establecer el cero absoluto de temperaturas.
definir el concepto de magnitud termométrica.
definir el concepto de temperatura.
establecer los puntos fijos de la escala Celsius de temperatura.
T.11 ¿Qué propiedad termométrica utiliza el termómetro de gas a volumen constante?
2 A.
2 B.
× C.
2
2 D.
La longitud.
El volumen.
La presión.
La densidad.
Lo que se mide es la presión del gas mantenido a volumen constante.
Fı́sica II - Segunda Prueba de Control
Mayo de 2011
APELLIDOS:
NOMBRE:
T.12 En un calorı́metro adiabático que contiene 500 g de agua a 20o C se introduce una masa
de hielo a -4o C. En el estado final de la mezcla se comprueba que se ha fundido justo la
mitad del hielo. ¿Qué masa de hielo se ha usado?. Datos: Calor especı́fico del agua: ca = 1
cal/g·K, del hielo: ch = 0, 5 cal/g·K y calor latente de fusión del hielo: Lf = 80 cal/g.
2 A.
× B.
2
2 C.
2 D.
250 g
238 g
263 g
244 g
Si llamamos: ma = 500 g, Ta = 20 o C, Th = −4 o C y T0 = 0 o C Se puede imponer que el
agua cede un calor igual al absorbido por el hielo mediante la ecuación: mh ch (T0 − Th ) +
0, 5mh Lf = ma ca (Ta − T0 ), donde mh es la masa de hielo que se ha añadido. Ésta es la
incógnita a despejar.
T.13 Sea un gas ideal que, a partir de ciertas condiciones de equilibrio iniciales, absorbe una
cantidad determinada de calor a presión constante alcanzando cierta temperatura final. Si
el gas, a partir de las mismas condiciones iniciales, hubiese absorbido ese mismo calor a
volumen constante habrı́a alcanzado una temperatura final...
2 A.
2 B.
× C.
2
2 D.
menor.
igual.
mayor.
mayor, igual o menor. Depende del gas.
Si imponemos que los calores absorbidos en ambos procesos son iguales: Qv = Cv ∆T1 =
Qp = Cp ∆T2 , como en un gas Cp > Cv se deduce que ∆T1 > ∆T2 . Es decir, el gas
experimenta un mayor incremento de temperatura en el proceso a volumen constante.
Alternativamente puede pensarse en términos del Primer Principio: en el proceso a volumen
constante todo el calor absorbido se invierte en incrementar la energı́a interna del gas
(Qv = ∆U = Cv ∆T ). Por contra, a presión constante parte de la energı́a absorbida como
calor se invierte en trabajo de expansión (negativo) y en consecuencia el incremento de
energı́a interna (y por tanto de temperatura) será menor para el mismo calor absorbido.
T.14 Un gas ideal parte de una condiciones iniciales de equilibrio y experimenta un proceso de
compresión de manera que en el estado final su presión se ha multiplicado por 2 mientras
que su volumen se ha visto reducido a la mitad. En ese proceso, la energı́a interna del
gas...
× A.
2
2 B.
2 C.
2 D.
no ha cambiado.
ha aumentado.
ha diminuido.
puede haber variado, pero con estos datos no se puede saber si aumenta o disminuye.
En este proceso se conserva el producto de presión por volumen: Pi Vi = Pf Vf . Entonces, en
virtud de la ecuación de estado del gas ideal (P V = nRT ) se deduce que las temperaturas
inicial y final son iguales: Ti = Tf . Como la energı́a interna de una gas ideal es función
exclusivamente de su temperatura podemos decir que en este proceso ∆U = 0.