9 SISTEMAS EXPERTOS
Anuncio

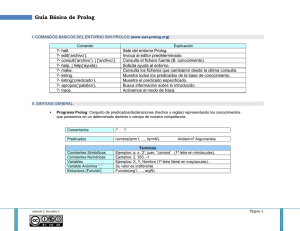
9 SISTEMAS EXPERTOS En este capítulo abordaremos uno de los productos típicos de la Inteligencia Artificial: los Sistemas Expertos. Normalmente, usamos herramientas de desarrollo conocidas con shells para construir este tipo de sistemas, pero si necesitamos configurar un shell para una aplicación en particular, es necesario conocer como es que un sistema experto se construye desde cero. El capítulo constituye el segundo ejemplo del uso de Prolog para resolver problemas típicos de la Inteligencia Artificial. Los sistemas expertos (SE) son aplicaciones de cómputo que involucran experiencia no algorítmica, para resolver cierto tipo de problema. Por ejemplo, los sistemas expertos se usan para el diagnóstico al servicio de humanos y máquinas. Existen SE que juegan ajedrez, que planean decisiones financieras, que configuran computadoras, que supervisan sistemas de tiempo real, que deciden políticas de seguros, y llevan a cabo demás tareas que requieren de experiencia humana. Los SE incluyen componentes del sistema en sí e interfaces con individuos con varios roles. Esto se ilustra en la figura 26. Los componentes más importantes son: • Base de conocimientos. La representación declarativa de la experiencia, muchas veces en forma de reglas IF-THEN. • Almacén de trabajo. Los datos específicos al problema que se está resolviendo. • Máquina de inferencia. El código central del SE que deriva recomendaciones con base en la base de conocimientos y los datos específicos del problema. • Interfaz del usuario. El código que controla el diálogo entre el usuario y el SE. Para entender un SE es necesario entender también el rol de los usuarios que interaccionan con el sistema: • Experto del Dominio. El o los individuos que son los expertos en resolver el problema que el SE intentará resolver. • Ingeniero de Conocimiento. El individuo que codifica el conocimiento de los expertos en forma declarativa, para que pueda ser usado por el SE. • Usuario. El individuo que consultará el SE para obtener los consejos que esperaría de un experto del dominio. Muchos SE se producen en ambientes de desarrollo conocidos como shells. Un shell es un sistema que contiene la interfaz del usuario, un formato de conocimiento declarativo para la base de conocimientos y una máquina de inferencia. El ingeniero de conocimiento usa el shell para construir un SE que resuelve problemas en un dominio particular. Si el sistema se construye desde cero, o utilizando shells configurados para cierto tipo de aplicaciones, otro individuo entra en escena: 89 90 �������� �������� Usuario Experto en el Dominio Interface con el Usuario Experiencia Ingeniero del Conocimieno Máquina de Inferencia Base de Conocimiento Ingeniero en Sistemas Almacén de Trabajo Figura 26: Componentes de un sistema experto e interfases humanas • Ingeniero de Sistemas. La persona que construye la interfaz del usuario, diseña el formato declarativo de la base de conocimientos, e implementa la máquina de inferencia ¿adivinan cual es su rol? En realidad eso depende de la talla del proyecto: El ingeniero de conocimiento y el ingeniero del sistema, pueden ser la misma persona. El diseño del formato de la base de conocimientos y su codificación están íntimamente relacionados. Al proceso de codificar el conocimiento de los expertos, se le conoce como ingeniería del conocimiento. Siendo ésta una tarea complicada, se espera el uso de los shells haga posible la reutilización del conocimiento codificado. En estas sesiones nos concentraremos en la programación en Prolog de los SE al margen del uso de las shells. �.� ��������������� �� ��� �� Los SE poseen las siguientes características, en menor o mayor grado: • Razonamiento guiado por las metas y encadenamiento hacia atrás. Una técnica de inferencia que usa las reglas IF-THEN para descomponer las metas en submetas más fáciles de probar. • Manejo de incertidumbre. La habilidad del SE para trabajar con reglas y datos que no son conocidos con precisión. • Razonamiento guiado por los datos y encadenamiento hacia adelante. Una técnica de inferencia que usa las reglas IF-THEN para deducir soluciones a un problema a partir de los datos iniciales disponibles. • Representación de datos. La forma en que los datos específicos a un problema dado, son almacenados y accesados por el SE. • Interfaz del usuario. La parte del SE que se usa para una interacción más amigable con el usuario. �.� ��������������� �� ��� �� • Explicación. La habilidad del SE para explicar sus procesos de razonamiento y su uso en el cómputo de recomendaciones. �.�.� Razonamiento basado en metas El encadenamiento hacia adelante, o razonamiento basado en metas, es una forma eficiente de resolver problemas que pueden ser modelados como casos de “selección estructurada”; donde la meta del SE es elegir la mejor opción de entre varias posibilidades enumeradas. Por ejemplo, los problemas de identificación caen en esta categoría. Los problemas de diagnóstico tambien caben aquí, pues se trata de elegir el diagnóstico adecuado. El conocimiento se codifica en reglas que describen como es que cada caso posible podría ser seleccionado. La regla rompe el problema en sub-problemas. Por ejemplo, las siguientes reglas formarían parte de un SE para identificar aves: 1 IF 2 familia es albatros AND color es blanco THEN ave es albatros laysan. 3 4 5 6 7 IF 8 familia es albatros AND color es negro THEN ave es albatros de pies negros. 9 10 11 El sistema puede usar otras reglas para resolver las sub-metas planteadas por las reglas de alto nivel, por ejemplo: 1 IF 2 orden es tubonasales AND tamaño es grande AND alas es grandes anguladas THEN familia es albatros. 3 4 5 6 �.�.� Incertidumbre Es muy común en la resolución de problemas de selección estructurada, que la respuesta final no es conocida con total certeza. Las reglas del experto pueden ser vagas, o el usuario puede estar inseguro sobre sus respuestas. Esto es fácilmente observable en el diagnóstico médico. Los SE normalmente usan valores numéricos para representar certidumbre. Existen diveras maneras de definirlos y usarlos en el proceso de razonamiento. 91 92 �������� �������� �.�.� Razonamiento guiado por los datos Para muchos problemas no es posible enumerar las soluciones alternativas a las preguntas planteadas con antelación. Los problemas de configuración caen en esta categoría. El encadenamiento hacia adelante, o razonamiento guiado por los datos, usa reglas IF-THEN para explorar el estado actual en la solución del problema y moverse a estados más cercanos a la solución. Un SE para acomodar el mobiliario puede tener reglas para la ubicación de un mueble en particular. Una vez que un mueble ha sido colocado, se puede proceder con los demás. La regla para colocar la TV enfrente del sofá es como sigue: 1 2 3 4 5 6 IF no_colocada tv AND sofá en pared(X) AND pared(Y) opuesta a pared(X) THEN colocar tv en pared(Y). Esta regla toma un estado del problema con la televisión no situada y regresa un estado nuevo, donde la televisión ya ha sido colocada. Puesto que la televisión ya ha sido colocada en su lugar, esta regla no volverá a ser disparada por el SE. Otras reglas serán usadas para colocar el resto de los muebles hasta terminar. �.� ������ �� ������� �� ���������� �� ������ Como pueden haber adivinado, Prolog posee una máquina de inferencia por encadenamiento hacía atrás. Esta máquina puede usarse parcialmente para implementar algunos SE. Las reglas de Prolog serán usadas para representar conocimiento y su máquina de inferencia será usada para derivar conclusiones. Otras partes del sistema, como la interfaz con el usuario deberán escribirse usando Prolog. Usaremos el problema de identificación de aves norteamericanas para ilustrar la construcción de un SE con Prolog. La experticia del SE se basa en un subconjunto de las reglas reportadas en Birds of North America de Robbins, Bruum, Zim y Singer 1 . Las reglas del SE estarán diseñadas para ilustrar como se pueden representar varios tipos de conocimiento, en vez de buscar una identificación precisa de las aves. �.�.� Reglas Las reglas de un SE normalmente toman el siguiente formato: 1 2 3 4 5 6 IF primera premisa AND segunda premisa AND ... THEN conclusión 1 La versión extendida en línea de este libro puede encontrarse en http://bna.birds.cornell.edu/bna/ �.� ������ �� ������� �� ���������� �� ������ La parte IF de la regla se conoce con el lado izquierdo de la regla (LHS), y la parte del THEN se conoce como el lado derecho de la regla (RHS). Esto es equivalente a la semantica de la regla Prolog: 1 2 3 4 conclusión :primera premisa, segunda premisa, ... Esto puede ser confuso pués la regla en prolog dice más THEN-IF que IF-THEN. Retomemos los ejemplos anteriores, si queremos representar en Prolog la regla: 1 IF 2 familia es albatros AND color es blanco THEN ave es albatros laysan 3 4 5 Tendríamos que escribir: 1 2 3 ave(albatros_laysan) :familia(albatros), color(blanco). Las siguientes reglas distinguen entre dos tipos de albatros y cisne (Ver la figura 27). Todas son cláusulas del predicado ave/1: 1 2 3 4 5 6 7 8 9 10 11 12 ave(albatros_laysan) :familia(albatros), color(blanco). ave(albatros_patas_negras) familia(albatros), color(obscuro). ave(cisne_silbador) :familia(cisne), voz(suave_musical). ave(cisne_trompetero) :famila(cisne), voz(alta_trompeta). :- Para que estas reglas tengan éxito al distinguir un ave, necesitamos almacenar hechos acerca del ave que deseamos identificar con el SE. Por ejemplo, si agregamos estos hechos al programa: 1 2 familia(albatros). color(obscuro). Ahora podemos usar la pregunta siguiente: ?- ave(X). X = albatros_patas_negras Yes 93 94 �������� �������� Figura 27: Cisne Trompetero en ilustración de John James Audubon (1838). Observen que aún en esta etapa temprana tenemos un SE completo, donde la experticia consiste en distinguir entre cuatro aves. La interfaz con el usuario es el REPL de Prolog y los datos de entrada se almacenan directamente en el programa. �.�.� Reglas para relaciones jerárquicas El siguiente paso será representar la naturaleza jerárquica del sistema de clasificación de un ave. Esto incluirá reglas para identificar la familia y el orden del ave. Continuando con el albatros y el cisne, los predicados para orden/1 y familia/1 son: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 orden(nariz_tubular) :fosas(externas_tubulares), habitat(mar), pico(gancho). orden(acuatico) :patas(membrana), pico(plano). familia(albatros) :orden(nariz_tubular), tamaño(grande), alas(muy_largas). familia(cisne) :orden(acuatico), cuello(largo), color(blanco), vuelo(pesado). Ahora el SE puede identificar al albatros a partir de observaciones fundamentales sobre el ave. En la primer versión, familia/1 fue implementada como un hecho. Ahora familia/1 es implementada como una regla. Los hechos del SE ahora reflejan más datos primitivos: �.� ������ �� ������� �� ���������� �� ������ 1 2 3 4 5 6 fosas(externas_tubulares). habitat(mar). pico(gancho). tamaño(grande). alas(muy_largas). color(obscuro). La consulta siguiente reporta: ?- ave(X). X = albatros_patas_negras Yes �.�.� Reglas para otras relaciones El ganso canadiense puede usarse para agregar complejidad al sistema. Debido a que esta ave pasa los veranos en Canadá y los inviernos en los Estados Unidos, su identificación se ve afectada por donde ha sido vista y en que estación. Dos reglas serán necesarias para cubrir estas situaciones: 1 2 3 4 5 6 7 8 9 10 11 12 ave(ganso_canadiense) :familia(ganso), estacion(invierno), pais(estados_unidos), cabeza(negra), pecho(blanco). ave(ganso_canadiense) :familia(ganso), estacion(verano), pais(canada), cabeza(negra), pecho(blanco). Estas metas pueden hacer referencia a otros predicados en una jerarquía diferente: 1 2 3 4 5 6 pais(estados_unidos) :- region(oeste_medio). pais(estados_unidos) :- region(sur_oeste). pais(estados_unidos) :- region(nor_oeste). pais(estados_unidos) :- region(atlantico_medio). pais(canada) :- provincia(ontario). pais(canada) :- provincia(quebec). 7 8 9 10 region(nueva_inglaterra) :estado(X), member(X,[massachusetts, vermont, connecticut, maine]). 11 12 13 14 region(sur_oeste) :estado(X), member(X,[florida, mississippi, alabama, nueva_orleans]). 95 96 �������� �������� Figura 28: Pato común del norte (Mallard) en ilustración de John James Audubon (1838). Otras aves necesitarán de predicados múltiples para ser identificada. Por ejemplo, el Mallard (Anas platyrhynchos) macho, o pato común del norte (Figura 28), tiene la cabeza verde con un anillo blanco; la hembra tiene la cabeza café moteada: 1 2 3 4 5 6 7 8 ave(mallard):familia(pato), voz(graznido), cabeza(verde). ave(mallard) :familia(pato), voz(graznido), cabeza(cafe_moteada). Basicamente, cualquier situación del libro de las aves norte americanas puede ser expresado fácilmente en Prolog. Las reglas expresadas forman la base de conocimientos del SE. El único punto débil del programa es su interfaz con el usuario, que requiere que los datos sean introducidos como hechos del programa. �.� �������� ��� ������� El sistema puede mejorarse considerablemente si proveemos una interfaz para el usuario, que pregunte por la información cuando esto sea necesario, en lugar de forzar al usuario a introducirla como hechos del programa. Antes de pensar en un predicado pregunta, es necesario entender la estructura de los datos que serán preguntados. Todos los datos, manejandos hasta ahora, han sido de la forma atributo–valor. Por ejemplo, los atributos del pato del norte Mallard, son mostrados en el Cuadro 2. atributo familia voz cabeza valor pato graznido verde �.� �������� ��� ������� Cuadro 2: Atributos valor para el mallard Esta es una de las representaciones más simples usadas en los SE, pero es suficiente para muchas aplicaciones. Existen representaciones más expresivas, como los tripletes objeto–atributo–valor, o las redes semánticas, o los marcos. Como estamos programando en Prolog, la riqueza del lenguaje puede usarse directamente en el SE. Por ejemplo, los pares atributo–valor han sido representados como predicados unarios de la forma atributo(valor): familia(pato), voz(graznido), cabeza(verde). Pero en region/1 usamos la membresia en listas para su definición. Usaremos el predicado pregunta para determinar con ayuda del usuario, cuando un par atributo–valor es verdadero. El SE debe modificarse para determinar que atributos son verificables por el usuario. Esto se logra con reglas para los atributos que llaman a pregunta: 1 2 3 4 5 6 7 8 9 fosas(X) :- pregunta(fosas,X). habitat(X) :- pregunta(habitat,X). pico(X) :- pregunta(pico,X). tamano(X) :- pregunta(tamano,X). come(X) :- pregunta(come,X). pies(X) :- pregunta(pies,X). alas(X) :- pregunta(alas,X). cuello(X) :- pregunta(cuello,X). color(X) :- pregunta(color,X). Ahora, si el SE tiene como meta probar color(blanco), llamará a pregunta/2 en lugar de consultar su base de conocimientos. Si pregunta(color, blanco) tiene éxito, entonces color(blanco) también lo tiene. La pregunta es como sigue: 1 2 3 4 pregunta(Atrib,Val):write(Atrib:Val), write(’? ’), read(si). El predicado read/1 tendrá éxito sólo si el usuario responde “si” y falla si el usuario responde cualquier otra cosa. Ahora el programa puede ser ejecutado sin datos de trabajo iniciales. La misma llamada a ave/1 inicia la consulta al SE. ?- ave(X). fosas:externas_tubulares? si. habitat:mar? si. pico:gancho? si. tamano:grande? si. alas:muy_largas? si. color:blanco? si. X = albratros_laysan Yes. 97 98 �������� �������� El problema con este enfoque es que si el usuario responde “no” a la última pregunta, la regla para ave(albratros_laysan) falla, llevandonos a un backtracking. De esta manera el SE nos preguntaría nuevamente información que ya sabe. De alguna manera deberíamos implementar un predicado pregunta que recuerde lo preguntado. ?- ave(X). fosas:externas_tubulares? si. habitat:mar? si. pico:gancho? si. tamano:grande? si. alas:muy_largas? si. color:blanco? no. fosas:externas_tubulares? si. habitat:mar? si. pico:gancho? si. tamano:grande? si. alas:muy_largas? si. color:obscuro? si. X = albratros_patas_negras Yes. Definiremos un nuevo predicado conocido/3 que nos ayude a recordar las respuestas del usuario. Las respuestas no se guardarán directamente en memoria, sino que serán guardadas dinámicamente con asserta/1 cuando pregunta provea información nueva para el SE: 1 pregunta(A,V) :- conocido(si,A,V), !. 2 3 pregunta(A,V) :- conocido(_,A,V), !, fail. 4 5 6 7 8 9 10 pregunta(A,V) :write(A:V), write’? : ’), read(Resp), asserta(conocido(Resp,A,V)), Resp == si. También es posible utilizar menues contextuales para el caso de atributos multivariados. La idea es que para atributos de un solo valor, la interfaz por el usuario pregunte una sola vez: 1 2 3 4 5 6 pregunta(A,V) :not(multivariado(A)), conocido(si,A,V2), V \== V2, !, fail. Una guía sobre los valores válidos para un atributo se implementa con el predicado menu_pregunta que trabaja de manera análoga a pregunta: 1 2 3 4 �.� �� ����� ������ tamaño(X) :menu_pregunta(tamaño, X, [grande, mediano, pequeño]). color(X) :menu_pregunta(color,X,[blanco,verde,cafe,negro]). La definición de menu_pregunta/3 es: 1 2 3 4 5 6 7 8 menu_pregunta(A,V,MenuLista) :write(’Cual es el valor para ’, write(A), write(’? ’), nl, write(MenuLista),nl, read(Resp), checar(Resp,A,V,MenuLista), asserta(conocido(si,A,X)), X == V. 9 10 11 checar(X,A,V,MenuLista) :member(X,MenuLista), !. 12 13 14 15 �.� checar(X,A,V,MenuLista) :write(’Ese valor no es válido, intente nuevamente’), nl, menu_pregunta(A,V,MenuLista). �� ����� ������ El ejemplo de identificación de aves tiene dos partes: una base de conocimientos, que incluye la información específica sobre las aves; y los predicados para controlar la interfaz con el usuario. Al separar estas dos partes, podemos crear un shell de SE. Con ello podemos crear un nuevo SE que identifique, por ejemplo, peces y reutilizar la parte de control de la interfaz. Un cambio mínimo es necesario para separar las dos partes de nuestro SE. Necesitamos un predicado de alto nivel que inicie el proceso de identificación. Puesto que no sabemos de antemano lo que el SE va a identificar, el shell buscará satisfacer un predicado llamado meta. Cada base de conocimiento deberá tener definido meta/1, por ejemplo, para el caso de identificación de aves tendríamos: 1 meta(X) :- ave(X). como primer predicado en la base de conocimientos aves. El shell tendrá un predicado solucion/0 que llevará a cabo labores de mantenimiento del SE, para luego resolver la meta/1: 1 2 3 4 5 solucion :abolish(conocido,3), define(conocido,3), meta(X), write(’La respuesta es: ’), write(X), nl. 6 7 8 solucion :write(’No se encontró una respuesta.’), nl. 99 100 �������� �������� El predicado Prolog abolish/2 se usa para eliminar los hechos definidos previamente con conocido/3, cada vez que una consulta se va a ejecutar. Esto permite al usuario ejecutar solucion multiples veces en una sola sesión. El predicado define/2 permite indicarle a Prolog que conocido estará definido en el SE, de forma que no cause error la primera utilización de este predicado. Este predicado puede variar dependiendo de la versión de Prolog utilizada. De esta manera tenemos que el SE ha sido dividido en dos partes. Los predicados en el shell son: • solucion, • pregunta, • menu_pregunta, • los predicados auxiliares de éstos. Los predicados en la base de conocimientos son: • meta, • las reglas sobre el conocimiento del SE, • las reglas sobre los atributos provistos por el usuario, • las declaraciones de los atributos multi-variados. Para usar este shell en Prolog, tanto el shell como la base de conocimientos deben ser cargados: 1 2 3 4 5 6 ?- consult(shell). yes ?- consult(’aves.kb’). yes ?- solucion. fosas_nasales : externas_tubulares ? ... �.�.� REPL El shell puede ser mejorado construyendo un ciclo de comandos read-eval-print loop. Para ello definiremos el predicado se: 1 2 3 4 5 6 7 8 se :bienvenida, repeat, write(’> ’), read(X), do(X), X == quit. �.� �������������� ����� ����� ��� ������������� Interfaz del Usuario se pregunta menu_pregunta Máquina de inferencia solucion cargar Base de Conocimientos Memoria de trabajo meta reglas mulivaluado preguntado conocido Figura 29: El shell del SE. 9 10 11 bienvenida :write(’Este es el shell de su SE.’), nl, write(’Escriba: cargar, consultar, o salir en el prompt.’), nl 12 13 14 do(cargar) :cargar_bd, !. 15 16 17 do(consultar) :solucion, !. 18 19 do(salir). 20 21 22 23 24 do(X) :write(X), write(’ no es un comando válido.’), nl, fail. 25 26 27 28 29 cargar_bd :write(’Nombre del archivo: ’), read(F), reconsult(F). La arquitectura obtenida de esta forma se muestra en la figura 29. �.� �������������� ����� ����� ��� ������������� Como hemos mencionado, el encadenamiento hacía adelante resulta conveniente cuando los problemas a resolver son del tipo selección estructurada, como en el ejemplo de la clasificación de aves. Sin embargo, en además de que hemos asumido que la información completa está disponible para resolver el problema, también hemos asu- 101 102 �������� �������� mido que no hay incertidumbre, ni el los datos provistos por el usuario, ni en las reglas de los expertos. Por ejemplo, el albatros puede ser observado en la bruma, con lo que sería difícil precisar si su color es blanco u obscuro. Es de esperar que un SE que maneje incertidumbre, pueda contender con este tipo de problemas. Desarrollaremos un shell que permita manejar reglas con incertidumbre y encadenamiento de ellas hacía atrás. Evidentemente, este SE tendrá un formato de reglas propio, diferente a las reglas de Prolog, y por lo tanto, una máquina de inferencia propia. �.�.� Factores de certidumbre La forma más común de trabajar con la incertidumbre consiste en asignar un factor de certidumbre a cada pieza de información en el SE. La máquina de inferencia deberá mantener los factores de incertidumbre conforme el proceso de inferencia se lleve a cabo. Por ejemplo, asumamos que los factores de certidumbre (precedidos por cf) son enteros entre -100 (definitivamente falso) y +100 (definitivamente verdadero). La siguiente base de conocimientos en formato del SE está diseñada para diagnosticar un auto que no enciende. Esto ilustra el comportamiento de los factores de certidumbre: 1 GOAL problema. 2 3 4 5 6 RULE 1 IF not arranca AND bateria_mala THEN problema is bateria. 7 8 9 10 RULE 2 IF luces_debiles THEN bateria_mala cf 50. 11 12 13 14 RULE 3 IF radio_debil THEN bateria_mala cf 50. 15 16 17 18 19 RULE 4 IF arranca AND olor_gasolina THEN problema is fuga cf 80. 20 21 22 23 24 RULE 5 IF arranca AND indicador_gasolina is vacio THEN problema is tanque_vacio cf 90. 25 26 27 28 29 RULE 6 IF arranca AND indicador_gasolina is bajo THEN problema is tanque_vacio cf 30. 30 31 32 ASK arranca MENU (si no) 33 �.� �������������� ����� ����� ��� ������������� PROMPT ’Su motor arranca? ’. 34 35 36 37 ASK luces_debiles MENU (si no) PROMPT ’Sus luces están débiles? ’. 38 39 40 41 ASK radio_debile MENU (si no) PROMPT ’Su radio está débil? ’. 42 43 44 45 ASK olor_gasolina MENU (si no) PROMPT ’Huele a gasolina?’. 46 47 48 49 ASK indicador_gasolina MENU (vacio, medio, lleno) PROMPT ’Que indica al aguja de gasolina? ’. Por el momento la inferencia usaría encadenamiento hacía atrás, similar al que usa Prolog. La regla GOAL indica que el proceso buscará un valor para problema. La regla 1 causará que la sub-meta bateria_mala sea procesada, etc. Observen que las reglas especifican también factores de certidumbre. Las reglas 2 y 3 proveen evidencia de que la batería está en mal estado, pero ninguna es conclusiva al respecto. Un diálogo con este sistema sería como sigue: 1 2 3 4 5 6 7 8 9 10 11 consultar, reiniciar, cargar, listar, trazar, cómo, salida : consultar Su motor arranca? : si Huele a gasolina? : si Qué indica la aguja de la gasolina? : vacio problema-tanque-vacio-cf-90 problema-fuga-cf-80 problema resuelto Observen que a diferencia de Prolog, el sistema no se detiene al encontrar el primer posible valor para problema. En este caso se computan todos los valores razonables para problema y se reporta el valor de certidumbre asociado a estas soluciones. Recordemos que estos factores de certidumbre no son probabilidades, solo ponderan de alguna manera las respuestas. De igual manera, el usuario podría ofrecer factores de certidumbre sobre sus respuestas, por ejemplo: 1 2 3 4 5 : consultar ... Huele a gasolina? si cf 50 ... Existen diversas maneras de capturar el concepto de factor de certidumbre, pero todas ellas deben de confrontar las mismas situaciones básicas: 103 104 �������� �������� • Reglas cuyas conclusiones son inciertas, • Reglas cuyas premisas son inciertas, • Datos provistos por el usuario inciertos, • Combinación de premisas inciertas con conclusiones inciertas, • Actualizar los factores de incertidumbre en los datos almacenados en el espacio de trabajo, • Establecer un umbral sobre el cual las premisas se consideran conocidas. �.�.� Factores de certidumbre à la MYCIN MYCIN [5], uno de los SE más conocidos en IA, introduce factores de certidumbre diseñados para producir resultados intuitivos desde la perspectiva de los expertos. Revisemos el uso de estos factores por casos. El más simple, sería aquel donde las premisas son totalmente ciertas: 1 2 arranca cf 100. olor_gas cf 100. disparan la regla 4 y por tanto, problema fuga cf 80 deberá agregarse al almacén de trabajo. Sin embargo, este es un caso poco probable. Normalmente no estamos totalmente seguros de las premisas de una regla y lo normal sería tener hechos como: 1 2 arranca cf 80. olor_gas cf 50. Cuando esto sucede, la incertidumbre en las premisas de la regla debe combinarse con las de la conclusión de la misma de la siguiente manera: CF = CFregla ⇥ mı́n CFpremisa/100 Dado el ejemplo, la regla 4 se activaría con un cf = 50 (el mínimo de las dos premisas) y dada la fórmula anterior, agregaríamos problema fuga cf 40 al almacén de trabajo. Para que una regla dispare, su factor de certidumbre debe superar un umbral que normalmente se fija en 20. Así que bajo la definición anterior, la regla 4 dispararía. Si tuviésemos olor_gas cf 15, entonces la regla no dispararía. Ahora consideren el caso donde hay más de una regla que da soporte a cierta conclusión. En ese caso, cada una de las reglas que disparan contribuirá al factor de certidumbre de la conclusión. Si una regla dispara y la conclusión ya se encontraba en el almacén de trabajo, las siguientes reglas aplican: CF(X, Y) = X + Y(100 - X)/100. Ambos X, Y > 0 CF(X, Y) = X + Y/1 - mı́n(|X|, |Y|). CF(X, Y) = -CF(-X, -Y). Uno de X, Y < 0 Ambos X, Y < 0 �.� �������������� ����� ����� ��� ������������� Por ejemplo, si disparamos la regla 2 (luces débiles) con su premisa sin incertidumbre, tendríamos que agregar al almacén de trabajo bateria_mala cf 50. Luego si disparamos la regla 3 (radio débil), el factor de certidumbre de este hecho debe modificarse a bateria_mala cf 75. Lo cual resulta intuitivo (hay más evidencia de que la batería tiene problemas). Lo que también resulta intuitivo es que necesitamos programar nuestra propia máquina de inferencia. �.�.� Formato de las reglas Como programaremos nuestra propia máquina de inferencia, podemos elegir la estructura de hechos y reglas. Las reglas tendrán la estructura general: regla(Nombre, Premisas, Conclusion). El Nombre opera solo como un identificador de la regla. El lado izquierdo de la misma Premisas implica al lado derecho Conclusion (conclusión). Como usaremos encadenamiento hacía atrás, cada regla será usada para validar una pieza de información, de manera el RHS contiene una meta con su factor de certidumbre asociado: conclusion(Meta, CF). mientras que las premisas toman la forma de una lista de metas: premisas(ListaMetas). Las metas serán representadas, para comenzar, como pares atributo–valor: av(Atributo, Valor). cuando Atributo y Valor son átomos, la estructura general de las reglas se ve como: 1 2 3 regla(Nombre, premisas( [av(A1,V1), av(A2,V2), ... ] ), conclusion(av(Attr,Val), CF)). Por ejemplo, la regla 5 quedaría representada como: 1 2 3 regla(5, premisas([av(arranca,si), av(indicador_gasolina,vacio)]), conclusion(av(problema,fuga), 80)). Estas reglas no son fáciles de leer, pero tienen una estructura adecuada para ser procesadas por Prolog. Otras herramientas de Prolog como las gramáticas de cláusula definitivas (DCG) o la definición de operadores, puede ayudarnos a simplificar esta representación. 105 106 �������� �������� �.�.� La máquina de inferencia Dado el formato de las reglas del SE deseamos que la inferencia tome en cuenta los siguientes aspectos: • Combine los factores de certidumbre como se indico anteriormente. • Mantenga el espacio de trabajo con la información actualizada con las nuevas evidencias obtenidas. • Encontrar toda la información acerca de un atributo en particular cuando se pregunte por él, y poner esa información en el espacio de trabajo. Primero, los hechos serán almacenados en la memoria de trabajo de Prolog, con el siguiente formato: 1 hecho(av(A,V),CF). De forma que un predicado meta/2 haría la llamada para resolver un problema dado en estos términos. Por ejemplo, en el caso del arranque del auto, tendríamos como meta: 1 ?- meta(av(problema,X),CF). El predicado meta/2 debe de contender con tres casos: • El atributo–valor se conoce de antemano; • Existen reglas para deducir el atributo–valor; • Se debe preguntar al usuario. El sistema puede diseñarse para preguntar al usuario automáticamente por el valor de un atributo, ante la ausencia de reglas; o bien, se puede declarar que atributos pueden ser preguntados al usuario. Este último enfoque hace que el manejo de la base de conocimientos sea más explícito y provee mayor control sobre los diálogos usuario – SE. Podemos definir un predicado pregunta/2 para declarar el atributo a preguntar y la frase para ello: 1 pregunta(pais_residencia,’¿En qué país vive? ’). Veamos ahora los tres casos para meta/2. El primero de ellos ocurre cuando la información ya está en la memoria de trabajo: 1 2 3 meta(av(Atr,Val),CF) :hecho( av(Atr,Val), CF), !. El segundo caso se da cuando el valor del atributo no se encuentra en la memoria de trabajo, pero el es posible preguntar por ello al usuario: �.� �������������� ����� ����� ��� ������������� 1 2 3 4 5 6 meta(av(Atr,Val), CF) :\+ hecho( av(Atr,_),_), pregunta(Atr,Msg), preguntar(Atr,Msg), !, meta(av(Atr,Val), CF). Para ello, el predicado preguntar/2 interroga al usuario. El usuario responde con un valor para la atributo Atr y un factor de certidumbre asociado CF. El mensaje Msg da la información necesaria para guiar al usuario en estas consultas: 1 2 3 4 5 preguntar(Atr,Msg) :write(Msg), read(Val), read(CF), asserta(fact(av(Atr,Val),CF)). El tercer caso para meta/2 es cuando el valor del atributo es desconocido, pero se puede deducir usando las reglas definidas en el sistema, en ese caso la llamada es: 1 2 meta(Meta,CFactual) :buscaReglas(Meta,CFactual). Esta llamada hace uso de la máquina de inferencia que diseñaremos para nuestro SE con incertidumbre. El factor de certidumbre se etiqueta como actual, porque es posible que cambie de valor al ir aplicando las reglas definidas en el sistema. El predicado buscaReglas/2 se encarga de encontrar aquellas reglas cuya conclusión unifica con la Meta en cuestión y de actualizar el factor de certidumbre con base en las premisas de estas reglas. Si la Meta es un hecho conocido, no hay nada que hacer, sólo regresar true: 1 2 3 4 5 6 7 8 buscaReglas(Meta,CFactual) :regla(N, premisas(ListaPremisas), conclusion(Meta,CF)), probar(ListaPremisas,Contador), ajustar(CF,Contador,NuevoCF), actualizar(Meta,NuevoCF,CFactual), CFactual == 100, !. 9 10 11 buscaReglas(Meta,CF) :hecho(Meta,CF). Dada una lista de premisas pertenecientes a una regla encontrada para satisfacer la Meta del SE, es necesario que buscaReglas/2 las pruebe. Para ello definimos probar/2: 1 2 probar(ListaPremisas, Contador) :probAux(ListaPremisas, 100, Contador). 3 4 probAux([],Contador,Contador). 107 108 �������� �������� 5 6 7 8 probAux([Premisa1|RestoPremisas],ContadorActual,Contador) :meta(Premisa1,CF,Cont), Cont >= 20, probAux(RestoPremisas,Cont,Contador). El ajuste de los factores de certidumbre se lleva a cabo de la siguiente manera: 1 2 3 ajustar(CF1, CF2, CF) :X is CF1 * CF2 / 100, int_redondear(X,CF). 4 5 6 7 int_redondear(X,I) :X >= 0, I is integer(X + 0.5). 8 9 10 11 int_redondear(X,I) :X < 0, I is integer(X - 0.5). La actualización de la memoria de trabajo se lleva a cabo de la siguiente manera: 1 2 3 4 5 6 actualizar(Meta,NuevoCF,CF) :hecho(Meta,ViejoCF), combinar(NuevoCF,ViejoCF,CF), retract(hecho(Meta,ViejoCF)), asserta(hecho(Meta,CF)), !. 7 8 9 actualizar(Meta,CF,CF) :asserta(hecho(Meta,CF)). 10 11 12 13 14 15 combinar(CF1, CF2, CF) :CF1 >= 0, CF2 >= 0, X is CF1 + CF2*(100 - CF1)/100, int_redondear(X,CF). 16 17 18 19 20 21 22 combinar(CF1,CF2,CF) :CF1 < 0, CF2 < 0, X is -( -CF1-CF2*(100+CF1)/100), int_redondear(X,CF). 23 24 25 26 27 28 29 combinar(CF1,CF2,CF) :(CF1 < 0 ; CF2 < 0), (CF1 > 0 ; CF2 > 0), abs_minimum(CF1,CF2,MCF), X is 100 * (CF1 + CF2) / (100 - MCF), int_redondear(X,CF). �.� �������������� ����� ����� ��� ������������� �.�.� Interfaz con el usuario La interfaz con el usuario es muy parecida a la definida en la sección anterior. Se incluyen predicados auxiliares necesarios en su definición: 1 2 3 4 5 6 7 se :repeat, write(’consultar, cargar, salir’), nl, write(’: ’), read_line(X), ejec(X), X == salir. 8 9 10 11 ejec(consultar) :metas_principales, !. 12 13 14 15 ejec(cargar) :cargar_reglas, !. 16 17 ejec(salir). 18 19 %% % Auxiliares 20 21 22 23 24 25 26 metas_principales :meta_principal(Atr), principal(Atr), imprime_meta(Atr), fail. metas_principales. 27 28 29 30 31 principal(Atr) :meta(av(Atr,Val,CF)), !. principal(_) :- true. 32 33 34 35 36 37 38 39 40 41 imprime_meta(Atr) :nl, hecho(av(Atr,Val), CF), CF >= 20, salidap(av(Atr,Val),CF), nl fail. imprime_meta(Atr) :write (’Meta: ’), write(Attr), write(’ solucionada.’), nl, nl. 42 43 44 45 46 47 48 49 salidap(av(Atr,Val),CF) :output(Atr,Val,ListaImprimir), write(Atr-’cf’-CF), imprimeLista(ListaImprimir), !. salidap(av(Atr,Val),CF) :write(Atr-Val-’cf’-CF). 109 110 �������� �������� 50 51 52 53 imprimeLista([]). imprimeLista([X|Xs]) :write(X), imprimeLista(Xs).