Distancia focal de una lente convergente (método del
Anuncio

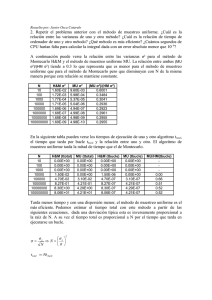
Distancia focal de una lente convergente (método del desplazamiento) Solucionario Tabla 1 S1/cm en fotografía 24,8 24,5 24,0 23,5 21,1 18,4 21,6 S2/cm en fotografía 25,0 24,6 24,0 23,4 21,0 18,4 21,3 Factor de escala, en la primera fotografía, fE1 S1 real/cm 60,0 18,2 60,0 18,3 81,8 60,0 20,2 60,0 20,3 72,8 50,0 18,9 50,0 18,8 63,5 50,0 20,3 50,0 20,3 57,9 50,0 21,4 50,0 21,3 49,3 50,0 21,5 50,0 21,5 42,8 40,0 21,2 40,0 21,1 40,8 S2 real/cm 82,0 72,7 63,8 57,6 49,3 42,8 40,4 S1 + S 2 en cm 2 d1/cm en fotografía 81,9 72,8 63,7 57,8 49,3 42,8 40,6 3,6 4,0 4,6 5,3 5,9 6,7 9,4 d2/cm en fotografía 21,5 20,5 19,3 18,3 15,1 11,7 11,6 d1 real/cm 11,9 11,9 12,2 13,1 13,8 15,6 17,7 d2 real/cm 70,5 60,6 51,3 45,1 35,4 27,2 22,0 d real d = d2-d1 en cm S2-d2 en cm2 58,6 48,7 39,1 32,0 21,6 11,6 4,3 3,29.103 2,93.103 2,53.103 2,32.103 1,96.103 1,70.103 1,63.103 4 S en cm 3,28.102 2,91.102 2,55.102 2,31.102 1,97.102 1,71.102 1,62.102 Factor de escala, en la segunda fotografía,fE2 S= Gráficas 1.- Con los valores de la tabla 1, represente en el eje Y (S2-d2), y en el eje X (4S). Determine la pendiente de la recta y el valor de la distancia focal imagen de la lente. lente convergente 2 2 (S -d )= 9,9945 (4S) - 4,2094 R2 = 0,9998 3,50E+03 2,50E+03 2,00E+03 2 2 S -d /cm 2 3,00E+03 1,50E+03 1,00E+03 5,00E+02 0,00E+00 1,00E+02 1,50E+02 2,00E+02 2,50E+02 3,00E+02 3,50E+02 4*S/cm La distancia focal de la lente convergente es f´ = 9,99 cm ≈ 10,0 cm 2.- En el apartado anterior la ordenada en el origen de la recta debe ser cero, pero el ajuste que haya hecho automáticamente la hoja de cálculo dará un valor diferente. Vuelva a hacer la representación del apartado 1 con la hoja de cálculo y ahora obligue a la recta a pasar por el origen de coordenadas. De la ecuación de esta recta, determine el valor de la distancia focal de la lente. Compare los dos valores obtenidos. (S2-d2) = 9,9775 (4S) R2 = 0,9998 lente convergente 3,50E+03 2,50E+03 2,00E+03 2 2 S -d /cm 2 3,00E+03 1,50E+03 1,00E+03 5,00E+02 0,00E+00 1,00E+02 1,50E+02 2,00E+02 2,50E+02 3,00E+02 4*S/cm La distancia focal es f´= 9,98 cm ≈ 10,0 cm 3,50E+02 3.- Represente en el eje de abscisas S frente a d2-d1 en el de ordenadas. Observe la curva y determine aproximadamente el valor de S cuando d2-d1 tiende a cero. Estime a partir de ese valor la distancia focal de la lente. Compárela con los valores obtenidos en los apartados anteriores. lente convergente 70 60 d/cm 50 40 30 20 10 0 30 40 50 60 70 80 90 S/cm De la gráfica anterior parece deducirse que cuando d =0, S = 40 cm. Si d = d2-d1 = 0, se deduce que d2 = d1 = 20 cm, esto nos indica que el objeto y la imagen se encuentran a la misma distancia del centro óptico de la lente y precisamente al doble de la distancia focal. Teniendo en cuenta la reversibilidad de la marcha de los rayos se deduce que la imagen y el objeto tienen el mismo tamaño. La distancia focal es aproximadamente, f´ = 10 cm , valor que está en buen acuerdo con los anteriores.