propuesta didáctica en formato pdf.
Anuncio

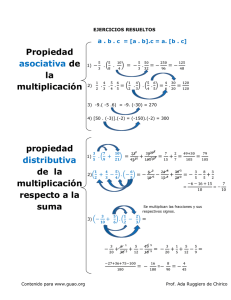
Propuesta didáctica: ¿De cuántas formas? Clase: 2º año Contenido programático: Producto de medidas (combinaciones) Autor: Maestras Milena Martín y Esther Moleri - Uruguay Educa. Tiempo de aplicación: El que cada docente estime conveniente. Descripción: Conjunto de cuatro actividades pensadas para trabajar uno de los significados de la multiplicación: producto de medidas, en 2º año. Se presentan cuatro problemas y algunas sugerencias didácticas que pueden resultar útiles. Propósitos: • Desarrollar y organizar el pensamiento combinatorio. (“Producto de medidas” – Vergnaud) • Percibir semejanzas en problemas en aparentemente distintos. • Crear condiciones que favorezcan la percepción de la multiplicación en ciertos problemas combinatorios. Criterios de evaluación: La evaluación sobre el aprendizaje logrado por los alumnos dependerá de lo que cada docente considere oportuno considerar. 1 Actividades: La secuencia Actividad 1 – Construcción de la “máquina de las posibilidades” Se les solicita a los alumnos que traigan a la clase vasos descartables como los de la imagen para construir la “máquina de las posibilidades”. Para realizar tal tarea pueden reunirse en duplas de compañeros o tríos. Procedimiento: • En uno de los vasos pegar dos etiquetas de diferente color, como lo ilustra la imagen. • En el segundo vaso pegar otras cinco, diferentes de las anteriores. Actividad 2 - El vestuario de Valentina Consigna: _______________________________________________________________ - Reunidos en duplas o ternas, leer el enunciado del siguiente problema y responder a la pregunta que plantea: Valentina tiene dos remeras de diferente color (rojo y verde) y cinco calzas: amarilla, rosada, roja, marrón y violeta. ¿De cuántas mareras diferentes podrá vestirse Valentina? - Comprobar que estén todas y comparar entre equipos de trabajo, la respuesta encontrada. ________________________________________________________________ 2 Cada uno de las etiquetas del vaso arriba expuesto representa el color de las remeras, y las etiquetas del segundo vaso, los colores de las calzas con las que Valentina podrá combinar su vestuario. Girando los vasos, fácilmente podrán reconocer todas las combinaciones posibles. Orientar a los estudiantes para que seleccionen una estrategia que les permita tener el control y registro de todas las combinaciones posibles, de manera de no repetir ninguna y de que todas estén contempladas. Puede ser empleando alguno de los programas de las XO como el Social Calc, el editor de texto, la actividad dibujar o la que cada dupla o trío considere óptimo. Una vez concluido el trabajo de los equipos, socializar las respuestas y compararlas para encontrar coincidencias y diferencias. Se recomienda, en esta etapa de la secuencia, hacer uso del video adjunto. Actividad 3 – ¿Cuántas parejas se pueden formar? Nuevamente empleando vasos descartables para facilitar la exploración de las combinaciones posibles, solicitarles a los alumnos que encuentren todas las parejas que se pueden formar partiendo de los nombres que ya se presentan sobre el material ilustrado en la siguiente imagen: 3 En uno de los vasos se pegan etiquetas con el nombre de tres varones, ejemplo Luis, Mauro y Joaquín. En el otro vaso, las etiquetas con el nombre de cuatro niñas: Laura, Carolina… -¿Cuántas parejas se pueden formar combinando los nombres presentados? -Si se agrega una niña más, ¿cuántas parejas más podrían formarse? -¿Pasaría lo mismo si se agregara un varón en vez de una niña? ¿Por qué? ________________________________________________________________ Actividad 4- El candado Para abrir un candado codificado es preciso conocer la combinación exacta de números que posibilita su apertura. Es preciso girar el disco de encima hasta colocar determinado algoritmo en la posición del medio. Después, es necesario hacer lo mismo con el disco de abajo. En cierto candado, en el disco superior se encuentran los números 1, 3, 5 y 7. En el inferior están los números 0, 2, 4 y 6. Para representar al candado del problema, recurriremos nuevamente a la “máquina de las posibilidades”. En este caso, las etiquetas tendrán registrados los números de cada uno de los discos del candado. 4 ________________________________________________________________ ¿Cuáles son los códigos posibles de formar combinando los dos discos? ¿Cuántos son? Registrar las respuestas. Los niños, luego de varios problemas, podrán utilizar progresivamente estrategias que les permitan organizar la información y “no olvidarse” de ninguna posibilidad. Posteriormente se analizará con los alumnos la pertinencia de resolverlos por medio de una multiplicación y finalmente reconocer que las escrituras 2 x 5 ó 5 x 2 también representan el problema (en el caso del vestuario de Valentina). Estos cálculos pueden ser propuestos por los alumnos o incorporados por el docente para someterlos a análisis. Asimismo se considera muy productivo, promover discusiones con ellos en torno a: - la necesidad de combinar todos los elementos con todos los otros, - cómo hacer para no olvidarse de ninguno, - la conveniencia de resolverlo de varias formas para estar más seguro, - la posibilidad de hacer dibujos, listas, cuadros de doble entrada, flechitas, etc. - la utilidad de ir anotando al lado números para después no confundirse al contar. - que luego de resolver el problema se pueden hacer al final las sumas o anotar cuál podría ser la multiplicación que resolvería el problema. Para que se produzcan avances en los procedimientos de resolución es necesario que los alumnos se enfrenten a este tipo de problemas durante cierto 5 tiempo y que el docente oriente la marcha de la clase hacia el control de la exhaustividad y la economización de estrategias. Por ejemplo, frente al problema de combinar dos remeras y cinco calzas, habrá niños que hagan listas, dibujos; otros encontrarán el resultado con sumas y probablemente, habrá quienes lo resuelvan con la multiplicación "2 x 5 ó 5 x 2". La introducción de variables didácticas que tornen antieconómico el empleo de "máquinas de posibilidades" u otro tipo de registro gráfico como cuadros de doble entrada o diagramas de árbol, promoverá en el alumno, la necesidad de recurrir al cálculo, como la estrategia ganadora, por ejemplo cuando desde la consigna se emplean números muy grandes. Ejemplo: ________________________________________________________________ En una fábrica se confeccionan prendas con 42 variedades de telas (algodón, sintético, imitación cuero, etc.) y de 89 colores diferentes. ¿Cuántas prendas de diferente tela y color podrán confeccionarse? ________________________________________________________________ Socializar todas las estrategias empleadas para llegar a la solución hará que se logren avances significativos. Para complementar lo que en esta secuencia se expuso, se recomienda acceder a los sitios sugeridos y consultar la bibliografía citada. Sitios sugeridos: Texto: “¿De cuántas formas? Combinatoria (Primera parte)” Texto: “Multiplicación de 1º a 6º”. Video: “Alterados por Pi – Capítulo 11” Sitio: "Matemática, ¿estás ahí? (Adrián Paenza) Sitio desde el que se puede acceder al libro de Adrián Paenza sobre números, problemas y curiosidades. Contempla además, contenidos relacionados con probabilidad. Incluye las soluciones de los problemas presentados. Texto: "El niño, las matemáticas y la realidad" - G. Vergnaud . 6 Texto: "Orientaciones didácticas para la enseñanza de la multiplicación en los tres ciclos de la EGB" Bibliografía: -SADOVSKY, Patricia: "Enseñar Matemática hoy. Miradas, sentidos y desafíos." Libros del Zorzal, Buenos Aires, 2005. -BELCREDI, Luis y ZAMBRA, Mónica: "Gauss 3. Matemática Tercer año del Ciclo Básico"- (Capítulo 6: "Estadística y Probabilidad"). La Flor de Itapebí, Montevideo, 2000. -RODRÍGUEZ, Milton: "Tratamiento de la estadística y la probabilidad a nivel escolar" en "Curso de Actualización en la Enseñanza de la Matemática para Inspectores de Educación Primaria. ANEP, Montevideo, 2003. -CHAMORRO, María del Carmen (Coordinadora): Matemáticas". Pearson Educación, Madrid, 2003. "Didáctica de las -VERGNAUD, Gérard: "El niño, las Matemáticas y la realidad. Problemas de la enseñanza de las Matemáticas en la escuela primaria". Editorial Trillas, México, 1991. Materiales: Seis vasos descartables o material similar. Etiquetas de diferentes colores. Adhesivo o pegamento. 7 Sugerencias: Variar los contextos en los que el contenido “producto de medidas” esté presente. Anexo: La combinatoria es una de las secciones de las matemáticas; ésta es necesaria para los representantes de las más diversas especialidades. Con los problemas combinatorios tienen que enfrentarse los físicos, los químicos, los lingüistas, los ingenieros y muchos otros trabajadores científicos-técnicos. El estudio de la combinatoria es la base para la solución de muchos problemas de la teoría de probabilidades y sus aplicaciones. Tradicionalmente, la enseñanza de la multiplicación fue pensada como contenido de segundo año bajo el supuesto de que los niños debían aprender primero a realizar las "cuentas", para luego aplicarlas en situaciones problemáticas. Aprender a multiplicar ha sido identificado con el aprendizaje de las “tablas” y las "cuentas". Hoy se sabe, sin embargo, que la construcción de conocimientos sobre la multiplicación no se logra cuando se aborda la enseñanza del algoritmo. Fácilmente se constata que muchos niños saben resolver los cálculos, pero no reconocen cuál es el conjunto de problemas que se resuelven con dicha operación. Asimismo, los niños pueden resolver problemas multiplicativos aún cuando no dominen estrategias de cálculo. Si aprender a multiplicar y a dividir no es terreno exclusivo de las cuentas, ¿qué significa entonces saber multiplicar y dividir? La construcción de estos conocimientos lleva varios años a los niños. ¿Cómo hacerlos “crecer” en cada año? ¿Cuáles son los diferentes tipos de problemas, los diversos procedimientos de resolución y estrategias de cálculo que se pueden abordar en cada ciclo? Ofrecer elementos para responder a estas preguntas es la finalidad de este documento. 8