¿Cuál es la distancia máxima que se puede recorrer, en una línea
Anuncio
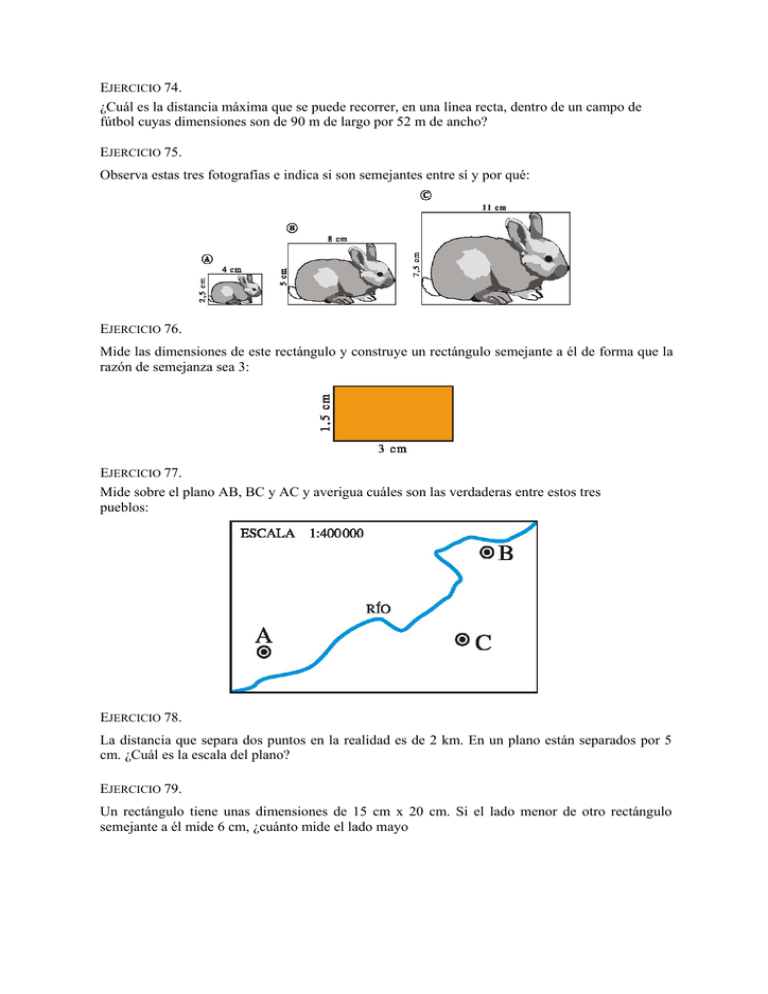
EJERCICIO 74. ¿Cuál es la distancia máxima que se puede recorrer, en una línea recta, dentro de un campo de fútbol cuyas dimensiones son de 90 m de largo por 52 m de ancho? EJERCICIO 75. Observa estas tres fotografías e indica si son semejantes entre sí y por qué: EJERCICIO 76. Mide las dimensiones de este rectángulo y construye un rectángulo semejante a él de forma que la razón de semejanza sea 3: EJERCICIO 77. Mide sobre el plano AB, BC y AC y averigua cuáles son las verdaderas entre estos tres pueblos: EJERCICIO 78. La distancia que separa dos puntos en la realidad es de 2 km. En un plano están separados por 5 cm. ¿Cuál es la escala del plano? EJERCICIO 79. Un rectángulo tiene unas dimensiones de 15 cm x 20 cm. Si el lado menor de otro rectángulo semejante a él mide 6 cm, ¿cuánto mide el lado mayo EJERCICIO 80. Sabiendo que las rectas a, b, c y d son paralelas calcula la longitud de x e y: EJERCICIO 81. Calcula el valor de x e y en esta construcción: EJERCICIO 82. Razona, apoyándote en los criterios de semejanza, por qué dos triángulos rectángulos con los catetos proporcionales son semejantes. EJERCICIO 83. Calcula la altura de un árbol que proyecta una sombra de 12 metros en el momento en que otro árbol que mide 2,5 m proyecta una sombra de 4 metros. EJERCICIO 84. Observa las medidas del gráfico y calcula la altura del faro: TERCERA EVALUACIÓN 9. Poliedros. EJERCICIO 85. Escribe el nombre de cada uno de los elementos de este poliedro: EJERCICIO 86. ¿Cuáles de las siguientes figuras son poliedros? ¿Por qué? EJERCICIO 87. Indica qué tipo de poliedro es cada uno de estos: EJERCICIO 88. Describe el siguiente poliedro y clasifícalo atendiendo a sus características: EJERCICIO 89. Las dimensiones de un ortoedro son a = 6 cm, b = 4 cm y c = 12 cm. Dibuja esquemáticamente su desarrollo y calcula su área. EJERCICIO 90. Las bases de un prisma recto son rectángulos de 6 x 8 cm. La altura del prisma es 16 cm. Dibuja su desarrollo y calcula el área total. EJERCICIO 91. Dibuja esquemáticamente el desarrollo de esta pirámide y calcula su área total sabiendo que su base es un cuadrado de 12 cm de lado y su arista lateral es de 15 cm: EJERCICIO 92. Dibuja de forma esquemática el desarrollo de este tronco de pirámide de base cuadrada y calcula su área total con las dimensiones del dibujo: EJERCICIO 93. Observa este poliedro. Indica por qué es regular, completa la tabla y dibuja esquemáticamente su desarrollo: EJERCICIO 94. ¿Qué poliedro regular está formado por ocho caras triangulares? Dibuja su desarrollo esquemáticamente. 10. Cuerpos de revolución EJERCICIO 95. Identifica cuáles de las siguientes figuras son cuerpos de revolución y nómbralos: EJERCICIO 96. Dibuja esquemáticamente el desarrollo de un cilindro de 2 m de radio y 8 metros de altura, y calcula su área lateral y su área total. EJERCICIO 97. Calcula el área lateral y el área total de un cono cuya generatriz mide 10 cm y el radio de su base es de 2,5 cm. Dibuja esquemáticamente su desarrollo y señala sobre él los datos necesarios. EJERCICIO 98. La generatriz de un tronco de cono mide 10 cm y sus bases tienen, respectivamente, 3 cm y 5 cm de radio. Calcula su área lateral y su área total. Dibuja esquemáticamente su desarrollo y señala sobre él los datos necesarios. EJERCICIO 99. Halla la superficie de una zona esférica de 40 cm de altura perteneciente a una esfera de 60 cm de radio. EJERCICIO 100. En una esfera escolar de 40 cm de radio están señaladas las zonas climáticas. Sabemos que cada casquete polar tiene 5 cm de altura y cada zona templada 10 cm de altura. Halla la superficie de cada zona climática. EJERCICIO 101. ¿Qué cantidad de chapa se necesita para construir un depósito cilíndrico cerrado de 0,7 m de radio de la base y 1 metro de altura? Dibuja esquemáticamente su desarrollo y señala sobre él los datos necesarios. EJERCICIO 102. Calcula el área lateral y el área total de un cono cuya generatriz mide 20 cm y el radio de su base es de 10 cm. Dibuja esquemáticamente su desarrollo y señala sobre él los datos necesarios. EJERCICIO 103. La generatriz de un tronco de cono mide 20 cm y sus bases tienen, respectivamente, 8 cm y 10 cm de radio. Calcula su área lateral y su área total. Dibuja esquemáticamente su desarrollo y señala sobre él los datos necesarios. EJERCICIO 104. Indica cuáles de las siguientes figuras son cuerpos de revolución y traza la figura plana que los genera: 11. Medida del volumen EJERCICIO 105. EJERCICIO 106. Expresa en cm3: a) 1 3 b) m 5400 3 c) mm 3 3 dam EJERCICIO 107. Expresa en distintas unidades (en forma compleja) o en una sola (en forma incompleja), según corresponda: 3 a) 256 895 450 cm 3 3 3 3 b) 3 km 234 hm 25 dam 2 m EJERCICIO 108. Calcula el volumen de estos cuerpos: EJERCICIO 109. Halla el volumen de este prisma cuyas bases son triángulos equiláteros: EJERCICIO 110. Calcula el volumen de una pirámide regular cuya base es un cuadrado de 8 cm de lado y su arista lateral es de 8 cm. EJERCICIO 111. Calcula el volumen de un cono cuya generatriz mide 12 cm y el radio de su base es de 5 cm. EJERCICIO 112. Calcula el volumen del tronco de pirámide y del tronco de cono: EJERCICIO 113. Teniendo en cuenta las medidas señaladas, calcula el volumen de esta figura: EJERCICIO 114. Para medir el volumen de una piedra pequeña utilizamos una vasija cilíndrica y echamos agua hasta su mitad. El diámetro interior de la vasija es de 10 cm y la altura que alcanza el agua es de 15 cm. Al introducir la piedra el nivel del agua sube 2 cm. ¿Cuál es el volumen de la piedra? 12. Funciones EJERCICIO 115. Escribe las coordenadas de los puntos A y B y sitúa en el eje de coordenadas los puntos C=(–2, 5) y D=(1, 3) EJERCICIO 116. Di cuál de las siguientes gráficas corresponde a una función y cuál no, e indica el porqué: EJERCICIO 117. Analiza la siguiente función y señala los intervalos constantes, los de crecimiento y los de decrecimiento: EJERCICIO 118. Halla algunos puntos de la función y = x + 3 y represéntala: EJERCICIO 119. Representa la siguiente función, indica qué tipo de función es y señala cuál es su pendiente: y = – 3x EJERCICIO 120. Representa la siguiente función, indica qué tipo de función es y señala cuál es su pendiente: EJERCICIO 121. Indica cuál es la pendiente de esta función. ¿Corta al eje Y? EJERCICIO 122. Señala cuál es la pendiente y el punto de corte con el eje vertical en la función: EJERCICIO 123. Indica cuál es la ecuación de esta función: EJERCICIO 124. Escribe la ecuación de una función que se represente mediante una recta paralela al eje horizontal y represéntala. 13. Estadística EJERCICIO 125. Estos son los meses en los que cumplen los años los 36 chicos y chicas de 2ºde ESO: a) Construye una tabla de frecuencias con estos datos. b) Realiza un diagrama de barras que represente estos datos. EJERCICIO 126. Estas son las velocidades a las que han pasado, un cierto día, los primeros 50 vehículos por una vía urbana: 22 54 81 24 51 36 18 28 34 65 28 49 57 49 65 37 39 56 73 83 67 39 23 64 75 23 45 65 71 34 15 63 34 87 39 28 32 72 34 21 54 73 95 94 38 46 23 89 24 63 a) Construye una tabla de frecuencias con estos datos agrupándolos en los intervalos de extremos: 0 - 20 - 40 - 60 - 80 - 100 b) Realiza el histograma correspondiente. c) ¿Cuántos vehículos han pasado a una velocidad superior a 60 km/h? d) ¿Cuántos no superaban los 40 km/h? e) Si la velocidad máxima permitida en esa vía es de 50 km/h, ¿cúantos vehículos han circulado por encima de esa velocidad? EJERCICIO 127. Halla la media, la mediana y la moda de las siguientes distribuciones de datos: a) 22, 26, 26, 26, 29, 29, 31, 32, 33 b) 101, 101, 105, 134, 134, 145, 145, 145, 166, 166 c) 7,5; 7,8; 7,8; 7,9; 7,9; 7,9; 8,2; 8,2 d) 45, 7, 23, 7, 4, 7, 23, 7, 23, 26, 7, 26, 32, 23, 7, 7







