Unidad 15. Integrales definidas. Aplicaciones.

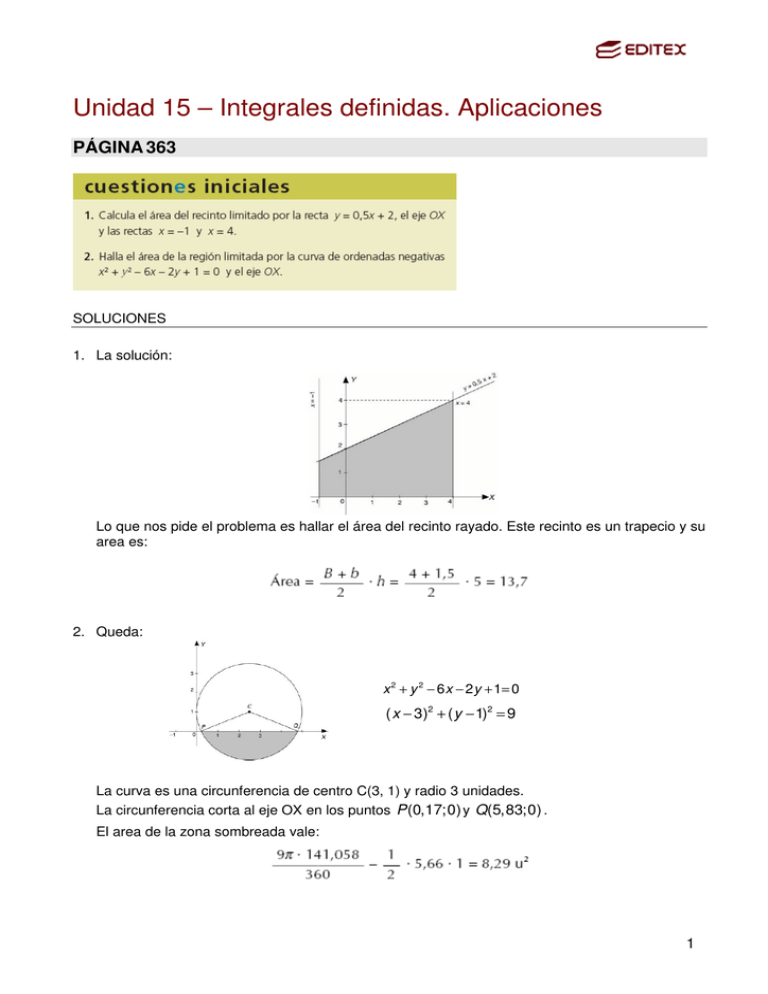
Unidad 15 – Integrales definidas. Aplicaciones
PÁGINA 363
SOLUCIONES
1. La solución:
Lo que nos pide el problema es hallar el área del recinto rayado. Este recinto es un trapecio y su
area es:
2. Queda:
x 2 + y 2 − 6 x − 2 y + 1= 0
( x − 3)2 + ( y − 1)2 = 9
La curva es una circunferencia de centro C(3, 1) y radio 3 unidades.
La circunferencia corta al eje OX en los puntos P (0,17; 0) y Q(5, 83; 0) .
El area de la zona sombreada vale:
1
PÁGINA 381
SOLUCIONES
1. Puesto que tanto el nombre de pila como los dos apellidos pueden comenzar por cualquiera de
las 26 letras del alfabeto, por el principio de multiplicación de la combinatoria tenemos
26 ⋅ 26 ⋅ 26 = 17 576 , conjuntos ordenados distintos de tres iniciales.
Por el principio de distribución, el numero minimo de habitantes necesarios para garantizar que
existen dos con las mismas iniciales será 17 577.
En esta situación los nidos son r = 17 576 , es decir, los conjuntos ordenados distintos de tres
iniciales; y las palomas son el número mínimo de habitantes, n = 17 577 .
2. Seleccionaremos una persona, digamos A. Mantiene correspondencia con las 16 restantes.
Como solamente hay tres temas, según el principio del palomar, debe escribirse al menos con
seis de ellas sobre el mismo tema.
Para fijar ideas, supongamos que A se escribe al menos con 6 de las restantes 16 sobre el tema
I. Si alguna de estas seis se escribe con otra sobre el tema I, entonces ya hay tres
escribiéndose sobre el tema I.
Supongamos que estas seis personas se escriben sobre los temas II y III. Si B es una de estas
seis, entonces, por el principio del palomar, debe escribirse al menos con tres de las otras 5
sobre uno de los dos temas, por ejemplo el tema II.
Ahora hay ds posibilidades para estas ultimas tres personas. Si alguna se escribe con otra sobre
el tema II, ya hemos encontrado tres personas que se escriben sobre el tema II. Si, por el
contrario, ninguna de las tres se escribe con las otras sobre el tema II, entonces las tres deben
escribirse entre si sobre el tema III, con lo que esta probada la afirmación del enunciado.
2
PÁGINA 386
3
SOLUCIONES
1. La suma superior es:
La suma inferior es:
2. La suma superior es:
s(P ) = (2 − 1) ⋅ 3 + (3 − 2) ⋅ 10 = 3 + 10 = 13
La suma inferior es:
s(P ) = (2 − 1) ⋅ 1+ (3 − 2) ⋅ 3 = 1+ 3 = 4
3. La solución es:
El teorema del valor medio dice que ∃c ∈ (0, 3) tal que:
Por tanto, como c ∈ (0, 3) , el valor pedido es c = 3
El teorema del valor medio dice que ∃c ∈ (0, 2) tal que
Obtenemos dos valores de C, pero esto no contradice el teorema, ya que este teorema
garantiza que exista un valor cero no dice que este valor sea único.
4
c) no es aplicable el teorema del valor medio ya que la función y = f (x ) no es continua en el
intervalo [- 1, 1], al cumplirse:
d)
Por el teorema de la media:
4. La solución es:
5
5. La solución queda:
a) la derivada es: F ′( x ) = 2e 4 x
2
El valor buscado es F ′(0) = 2 ⋅ e 4 ⋅ 0 = 2.
b) la derivada de la función F (x ) es F ′( x ) = ln x . Esta no se anula en el intervalo [2, 10]. La
derivada es positiva en intervalo citado.
Teniendo en cuenta los hechos anteriores la función F (x ) no tiene extremos relativos y si
extremos absolutos que se alcanzan en los extremos del intervalo.
Para F ( 2) = 0, 39 se obtiene el numero de la función y en F (10) = 14, 04 tiene máximo
absoluto.
c) En este caso:
d) F ′( x ) = x ⋅ cos x
2
e) G′( x ) = e − x (1+ x 2 )
2
2
f) F ′( x ) = e − x ; F ′′ ( x ) = − 2 ⋅ e − x ; F ′′′ ( x ) = ( 4 x 2 − 2) ⋅ e − x
2
Por tanto como F ′′ (0) = 0 y F ′′′ (0) ≠ 0 la función F(x) tiene un punto de inflexión en el punto
de abscisa 0.
g) F ′(x ) = e
x4
2
·2 x − e
x2
2
6
PÁGINA 387
7
SOLUCIONES
6. La solución queda:
6
a)
4 dx
x +3
∫
1
Calculamos la integral indefinida por integrales inmediatas:
Haciendo C = 0 y aplicando la regla de Barrow, obtenemos:
1
b)
ex
∫0 e x + 2 dx operando de forma análoga a las anteriores, obtenemos:
8
c)
3
dx operando de manera análoga a las anteriores, obtenemos:
1+ x
∫
0
3
d)
dx
∫ 1+ x
2
dx operando de forma análoga, obtenemos:
1
π2
π2
sen x
2
1
e) ∫
dx = ∫ sen x ⋅
dx =
3 0
2 x
0 3 x
8
2
f)
∫
0
dx
9 − x2
queda:
3
x3
g) ∫
dx determinamos la integral indefinida por el método de integración de funciones
( x − 1)2
2
racionales:
Determinamos la integral definida haciendo C = 0 y aplicando la regla de Barrow:
9
5
h)
∫
2
x2 +1
dx calculamos la integral indefinida por el método de integración de funciones
x3 − x
racionales:
Haciendo C = 0 y aplicando Barrow, obtenemos la integral definida:
9
i)
x
∫ x+
dx resolvemos la integral indefinida por cambio de variable, haciendo:
x
x = t 2 ⇒ dx = 2t dt .
4
10
π /2
∫ sen 2x ⋅ dx
j)
calculemos la integral indefinida:
0
1
∫ (x
k)
−1
4x
dx operando de forma análoga a las anteriores, obtenemos:
+ 2) 4
2
4
l)
∫
9 + 4 x dx operando de manera análoga a las anteriores, obtenemos:
0
2
m)
∫ 4x
2
(1+ x 3 )5 dx operando de manera análoga a las anteriores, obtenemos:
0
11
Calculamos la integral definida haciendo C = 0 y aplicando la regla de Barrow:
1
ñ)
x
x
∫ ( x − e cos x ) dx = ∫ x dx − ∫ e cos x dx =
0
x2
−l
2
12
1
o)
∫ (x
0
dx
dx
3
+ 1)
13
6
p)
∫x
x − 2 dx resolvemos la integral indefinida por el método de cambio de variable,
3
haciendo x − 2 = t 2 ⇒ dx = 2t dt .
3
q)
∫
2
x 4 + 2x − 6
dx resolvemos la integral indefinida por el método de integración de funciones
x 3 + x 2 − 2x
racionales:
14
5
r)
ln x
dx calculamos la integral indefinida:
x
3
∫
π /2
s)
∫ sen 2x ⋅ dx
calculamos la integral indefinida:
0
3
t)
dx
∫ x + b con b > 0 operando de forma análoga a las anteriores, obtenemos:
1
4
u)
∫
1
x −1
dx obtenemos la integral haciendo el cambio: x − 1= t 2 ⇒ dx = 2t dt .
x
15
π /4
v)
∫ tg x dx
calculamos la integral indefinida por el método de integrales inmediatas y después
−1
calculamos la definida haciendo C = 0 y aplicando Barrow.
3
w)
∫x
2
x
dx determinamos la integral indefinida por el método de integrales inmediatas y
−1
2
después la integral definida haciendo C = 0 y aplicando Barrow:
6
x)
∫
3
2x − 3
2x − 3 − 1
dx resolvemos la integral mediante el cambio: 2 x − 3 = t 2 ⇒ dx = t dt .
16
1
y)
∫
0
x2 −1
dx esta integral no está definida en [0, 1].
x
Resolvemos la integral indefinida en el campo complejo por el método de cambio de variable,
haciendo x 2 − 1= t 2 ⇒ dx =
t dt
.
x
1
z)
∫x
2
⋅ ln x dx esta integral no está definida en el intervalo [-1,1].
−1
17
7. Las integrales quedan:
b)
c)
d)
e)
f)
18
8. Las integrales quedan:
Ambas integrales son iguales a cero, pues al ser las funciones impares y simetricas respecto
al origen se anulan entre si las areas de las regiones que se obtienen.
9. El área viene dada por:
El área del recinto sombreado viene dada por:
Directamente este recinto es un trapecio y su area vale:
Con lo que queda comprobado el resultado anterior.
10. Queda:
Recinto sombreado:
19
PÁGINA 388
20
SOLUCIONES
11. Queda:
Queremos calcular el area del recinto sombreado:
12. La solución es:
El área pedida es la del recinto sombreado.
13. Queda:
El área del recinto limitado por la curva, el eje OX y las rectas x = −
π
2
y x=
π
2
vale:
21
14. La solución queda:
a)
b)
Las curvas y 2 = 9 x; y 2 = 4( x + 1) se cortan en los puntos de abscisa x = 0, 8 pues:
El área pedida es la de la zona sombreada y vale:
22
c)
Estas curvas se cortan en los puntos solución del sistema:
Otra forma de hallar el area del recinto buscado:
23
15. La solución es:
Las curvas se cortan en x = 0 y x = 1. Calculamos el area de la zona sombreada.
Resolvemos por el método de integración por partes la integral indefinida:
Haciendo C = 0 y aplicando la regla de Barrow, calculamos la integral definida que nos
permite calcular el area pedida:
24
16. La solución es:
El área del recinto sombreado buscado vale:
17. La solución:
El circulo de radio R queda limitado por la circunferencia de ecuación: x 2 + y 2 = R 2
R
Área = 4
∫
R 2 − x 2 dx
0
Calculamos la integral indefinida
∫
R 2 − x 2 dx mediante el cambio de variable:
25
Haciendo C = 0 y aplicando la regla de Barrow, calculamos la integral definida que nos da el
area del circulo buscado:
Calculamos la integral indefinida
Por el método de cambio de variable, para ello hacemos x = a sen t ⇒ dx = a cos dt
Haciendo C = 0 y aplicando la regla de Barrow, calculamos la integral definida que nos da el
área encerrada por la elipse dada:
26
18. Los volúmenes son:
b)
c)
19. Los volúmenes quedan:
a)
b)
c)
d)
27
20. El volumen es:
21. El volumen es:
22. el volumen de la esfera es:
23. el volumen del elipsoide es:
28
PÁGINA 389
29
SOLUCIONES
24. La suma superior es:
La suma inferior es:
25. Aplicando este teorema obtenemos :
26. La solución en cada caso es:
La primera derivada es:
La segunda derivada es:
27. La solución es:
a) La derivada es:
b) El límite produce una indeterminación del tipo
0
.
0
Aplicando la regla de L´Hopital obtenemos:
30
28. Las derivadas de la función son:
La primera derivada se anula y obtenemos:
En el punto (− 1, 0) , al ser F ′′( − 1) = 8 > 0 existe un minimo relativo.
En el punto (1, 0), al ser F ′′(1) = 8 > 0 existe un mínimo relativo.
En el punto (0, 2/3), al ser F ′′(0) = − 2 < 0 , existe un máximo relativo.
29. Tenemos que:
30. En cada caso queda:
a) haciendo el cambio e x = t , obtenemos:
31
31. La solución es:
Calculamos la integral indefinida por el método de interacion por partes:
32. El área es:
La zona sombreada es la región de plano limitada
por las curvas dadas.
32
33. Ecuacion de la recta tangente a f(x) = ln x, en el punto (e, 1):
33
34. La solución es:
Llamando d a la distancia buscada, se cumple:
A una distancia de 3 unidades.
35. La parábola y la recta se cortan en los puntos:
Ponemos el valor absoluto, pues el área puede ser diferente según sea a > 0 o a < 0.
34
La integral se resuelve del siguiente modo:
36. La superficie viene dada del siguiente modo:
El área de la zona sombreada viene dada por:
35
37. La superficie viene dada del siguiente modo:
Hallamos los puntos de inflexión:
Los puntos de inflexión son:
36
PÁGINA 390
37
SOLUCIONES
38. Haciendo la integral definida por partes obtenemos:
e
e
ln x
1
2
 1
∫1 x 2 dx =  − x ln x − x 1 = 1 − e = 0,2642
39. La solución es:
π
a) El área =
∫ x·senx·dx = ( − x cos x + sen x )
π
0
= π unidades cuadradas.
0
b) la recta tangente en el punto dado tiene por ecuación y = π ( x − π)
0
El área buscada es: Área =
∫ π ( x − π ) dx =
π
π3
= 15,50314 unidades cuadradas.
2
40. Imponiendo las condiciones del enunciado al polinomio tenemos el sistema:
3a + 2b + c = 0
b = 0

de donde obtenemos que a = −1 ; b = 0 ; c = 3 ; d = 1
d = 1
5
5

a
c
5
 + +1=
 4 2
4
Por tanto el polinomio es P ( x ) = −
1 3 3
x + x +1
5
5
41. Resolvemos esta integral por descomposición en fracciones simples y obtenemos:
a
2
  x + 3 2 
 5(a + 3) 
16
∫0 15 + 2x − x 2 dx = ln  x − 5   = ln  −3(a − 5) 

0
a
Igualando esta expresión a la que nos da el enunciado obtenemos que a puede tomar valores
3 y 9.
42. La solución es:
2
a)
∫
0
2
 5x 2 − 4 
4 − 2i
dx = 
no tiene soluciones reales.
 =
5
5

 0
5x 2 − 4
x
b) todas las primitivas son de la forma
5x 2 − 4
+ C imponiendo las condiciones del
5
enunciado obtenemos que la primitiva buscada es F ( x ) =
5x 2 − 4 4
+
5
5
38
43. La función dad es creciente en ( − ∞, 0 ) y decreciente en ( 0, + ∞ ).
 1 21   1
Tiene un máximo relativo en el punto (0,e) y dos puntos de inflexión en 
,e  y  −
,e2

2
2

 
1

.


Tiene una asíntota horizontal de ecuación y = 0.
Su grafica es:
3
∫ x·f ( x )·dx = ∫ x·e
1− x 2
Calculamos a integral pedida:
1
1
3
 e1− x 
e −1
·dx = 
= 0,5
 =
8
 −2 1 2e
2
3
44. En cada caso diremos:
•
f(x) es continua en [-2,-1] , por lo que aplicando el teorema del valor medio tenemos que
∃b ∈ [− 2,−1] tal que:
−1
∫ f (t )dt = f (b)( −1 + 2) = f (b)
−2
•
f(x) es continua en [1,2] , por lo que aplicando el teorema del valor medio tenemos que
2
∃c ∈ [1,2] tal que: ∫ f (t )dt = f (c )(2 − 1) = f (c )
1
De ambas igualdades concluimos que f (b ) = f (c ) con b ≤ -1 y c ≥ 1
45. La solución queda:
La cuerda tiene por ecuación y − e =
e2 − 1
( x − 1)
2e


e2 − 1
2
e
+
( x − 1) − e x dx = = 0,74
∫−1 
2e
e

e
Calculamos el area:
39
46. La solución es:
Aplicando el teorema fundamental del calculo integral obtenemos: F´( x ) =
senx
x
Por lo que las abscisas de sus extremos relativos en un periodo son:
π
3π
Máximo relativo en x = y mínimo relativo en x =
.
2
2
47. La solución es:
1
Aplicando la integración por partes obtenemos:
1
1
∫ f ( x )dx = [ x·f ( x )]0 − ∫ x·f ´( x )dx = f (1) −
0
0
1
1
=−
2
2
48. Imponiendo las condiciones del enunciado obtenemos:

b = 0

3 + 2a + b = 4 de donde a = 12 ; b = 0 ; c = 7 12
1 1
 + +c =1
4 6
49. La solución queda:
Aplicando el teorema fundamental del calculo integral obtenemos:
(
)
F´( x ) = x 2 − 1 ·e − x
2
y
(
)
F´´( x ) = 4 x − 2 x 3 ·e − x
2
La función es creciente en (− ∞,−1) ∪ (1,+∞ ) y decreciente en (-1 , 1)
(
) ( )
La función es cóncava hacia las y negativas en ( − 2,0 ) ∪ ( 2, +∞ )
La función es cóncava hacia las y positivas en −∞, − 2 ∪ 0, 2
40