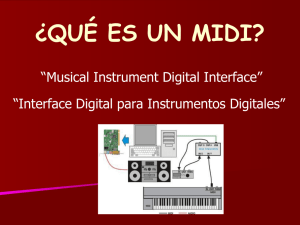
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES

SÍNTESIS DIGITAL DE
INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE
PIANOS ELECTRÓNICOS
DEPARTAMENTO DE
TEORÍA DE LA SEÑAL Y
COMUNICACIONES
CURSO 2004/2005
Autor: Daniel Gómez Díaz-Pinés
Tutor: Rubén Martín Clemente
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
1. Prólogo……………………………………………………………………. 3
2. Análisis del mecanismo del piano………………………………………... 5
2.1 Breve historia del piano………………………………………………. 6
2.2 Aspectos básicos de la acústica del piano……………………………. 8
2.3.Efectos de segundo orden…………………………………………….. 13
3. Afinación del piano. Introducción al sistema temperado………………… 20
3.1 Bases acústicas de la escala………………………………………….. 21
3.2 Proporciones interválicas ……………………………………………. 24
3.3 El sistema temperado………………………………………………… 28
4. Modelos de síntesis……………………………………………………….. 29
4.1. Modelos de señal…………………………………………………….. 30
4.1.1. Métodos de síntesis global…………………………………. 31
4.1.2. Métodos lineales………………………………………….... 46
4.1.3. Métodos de liberación de muestras………………………… 54
4.2. Modelos físicos………………………………………………………. 66
4.2.1. Método de diferencias finitas………………………………. 67
4.2.2. Síntesis modal……………………………………………… 72
4.2.3. Guiado digital de onda……………………………………... 73
5. El Sistema MIDI………………………………………………………….. 92
5.1 Aspectos básicos……………………………………………………… 93
5.2 Mensajes MIDI……………………………………………………….. 95
5.3 Secuenciadores y archivos MIDI……………………………………... 102
5.4 Sistema General MIDI (GM)…………………………………………. 104
6. Efectos de sonido comunes……………………………………………….. 105
6.1 Reverberación………………………………………………………… 106
6.2 Otros………………………………………………………………….. 117
7. Evolución y futuro de los métodos de síntesis…………………………….120
8. Análisis y síntesis de sonidos de piano……………………………………124
8.1. Análisis de sonidos PCM…………………………………………….. 124
8.2. Análisis de sonidos FM……………………………………………….129
8.3. Síntesis de sonidos FM………………………………………………. 131
Bibliografía…………………………………………………………………… 134
Apéndice……………………………………………………………………… 136
Agradecimientos……………………………………………………………… 139
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
1. PRÓLOGO
3
1. PRÓLOGO
Desde tiempos inmemoriales, la música ha jugado un papel muy
importante en todos los órdenes de la sociedad, tanto a nivel artístico como
humano y social. La música es característica de prácticamente todas las
culturas y civilizaciones, lo que sugiere que el instinto de hacer música es
fundamental en la naturaleza humana.
Con la aparición de la tecnología digital, se desarrollan los primeros
instrumentos electrónicos, dispositivos que intentan simular la respuesta
natural de un instrumento mecánico. En primer lugar, puede surgir la
pregunta: ¿por qué utilizar una copia, que por muy elaborada siempre será
imperfecta, pudiendo utilizar el original?. En este sentido los instrumentos
electrónicos poseen muchas ventajas respecto a los originales mecánicos.
En primer lugar, poseen siempre una afinación perfecta, ya que los
parámetros de dicha afinación se encuentran almacenados en un chip de
silicio y no son modificables por cualidades ambientales, atmosféricas o de
cualquier otro tipo. Además la afinación puede variarse en cualquier
momento sin más que modificar los parámetros numéricos de afinación
almacenados, lo cual resuelve de un plumazo los problemas de afinación al
interpretar piezas del repertorio antiguo, por no hablar del problema de la
afinación de un conjunto de instrumentos como puede ser una orquesta.
En segundo lugar, dado que la información relevante para la
generación del sonido se encuentra concentrada en un microprocesador
digital, el instrumento puede transportarse de manera cómoda, sobre todo
en el caso de un piano, con sus evidentes problemas de movilidad y
transporte. Dejando de lado características estéticas, el instrumento puede
implementarse con cualquier apariencia y forma, con tal de que el interfaz
sea el adecuado para la interpretación musical
Por último, pero no menos importante, la cuestión económica. Los
instrumentos tradicionales suelen construirse mediante un proceso de
elaboración laborioso que se basa generalmente en sistemas de fabricación
muy cercanos a la artesanía. Los instrumentos electrónicos, por el
contrario, pueden fabricarse en serie una vez que el prototipo ha sido
desarrollado, garantizando además una respuesta única y uniforme para
todos los ejemplares
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
1. PRÓLOGO
4
Por todo ello, gracias al desarrollo de los instrumentos electrónicos,
sería posible, por un espacio comparado a un escritorio de oficina y por un
precio no muy superior, disponer de un auténtico piano de concierto,
comparable al mejor de los Steinways y que además permanece siempre en
la más perfecta afinación.
Aunque la situación actual se encuentra lejos todavía de reproducir
de manera completamente fiel la respuesta de los instrumentos mecánicos,
el progreso imparable puede hacer que en un futuro no muy lejano, los
instrumentos electrónicos puedan reemplazar a los mecánicos en la
ejecución de alto nivel, sin prejuicio de la expresión artística. De hecho, ya
actualmente los estudios de grabación utilizan gran cantidad de técnicas de
procesamiento digital en sus grabaciones, algunas de las cuales se derivan
del estudio de la síntesis digital de los instrumentos involucrados.
En este trabajo se analizarán, haciendo hincapié en los sonidos de
piano en particular, los distintos métodos de síntesis, es decir los diferentes
algoritmos que logran producir sonidos realistas y musicalmente
interesantes en tiempo real. El propósito de este documento no es mostrar
con exactitud los detalles de cada método, sino ofrecer una visión de
conjunto de varios métodos de síntesis sonora. Las técnicas de síntesis
analizadas fueron elegidas como ejemplos representativos del modelo de
síntesis general al que se refieren.
No obstante, para comprender el motivo de determinadas
operaciones en los modelos de síntesis, es necesario realizar un estudio
previo, aunque somero, del instrumento objeto de estudio, El Piano, así
como del sistema musical occidental general, que es la base para cualquier
generación de sonidos, ya sea natural o artificial. Estos conceptos se
explican en capítulos previos a las técnicas de síntesis.
Posteriormente, y como complemento, es necesario incluir aspectos
relacionados con los instrumentos musicales digitales que, aunque no
intervienen directamente en la generación del sonido, son totalmente
imprescindibles para su elaboración y forman una parte importante del
resultado final, por lo que no pueden pasarse por alto. Estos aspectos son el
protocolo MIDI, indispensable para la comunicación entre el músico y el
sintetizador y los efectos sonoros, tan relevantes en la consecución de una
respuesta musical artísticamente satisfactoria.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
2. ANÁLISIS DEL MECANISMO DEL PIANO
5
2. ANÁLISIS DEL MECANISMO DEL PIANO
En este capitulo se analizarán los aspectos más relevantes de la
mecánica del piano que serán necesarios a la hora de sintetizar un sonido
realista del instrumento. Sólo se tendrán en cuenta las particularidades
asociadas con la generación del sonido, dejando de lado otros aspectos de
la mecánica relacionados con la técnica pianística (dureza de tecla,
transferencia de peso….) que, aunque muy importantes para la ejecución
pianística, no son objeto de estudio del presente trabajo.
Así pues se analizarán los distintos elementos generadores del
sonido: martillos, cuerdas, tabla armónica, apagadores…, focalizando
nuestra atención más en los efectos sonoros que producen cuya simulación
es el objetivo de todo modelo de síntesis, y menos en el mecanismo físico
que los producen, aunque en muchas ocasiones causa y efecto se
encuentran tan indisolublemente unidos que se hace absolutamente
necesario estudiar ambos en conjunto.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
2. ANÁLISIS DEL MECANISMO DEL PIANO
6
2.1. Breve historia del piano
Hasta el siglo XVIII convivieron tres grandes familias de
instrumentos de teclado. Los instrumentos de cuerda pinzada, como el
clave, virginal o espineta; los instrumentos de cuerda golpeada, como el
clavicordio; y finalmente el órgano, cuyo mecanismo de producción del
sonido lo asemeja más a la familia de los vientos.
El clavicordio, que puede considerarse el antecedente directo del
piano, permitía realizar matices dinámicos (piano, forte), realizar fraseo, e
incluso imitar a los cantantes en el vibrato. Su principal inconveniente era
su reducido volumen de emisión del sonido, lo que impedía la ejecución en
público, por pequeño que fuera el auditorio. De la búsqueda de un mayor
incremento dinámico y de riqueza de contrastes, surge en 1705, en los
talleres de un constructor de instrumentos de teclado llamado Cristofori, el
nuevo Gravicembalo col piano e forte que pronto fue conocido con el
nombre de fortepiano.
El fortepiano primitivo, no alcanzaba una gran sonoridad, ni una
elevada variedad tímbrica, pero poseía características que han llegado hasta
nuestros días como la percusión desde abajo, un sistema que permitiera a la
cuerda vibrar libremente tras la percusión, y una palanca suficientemente
larga y sensible para transmitir eficazmente las variaciones de velocidad
durante el descenso de la tecla.
Durante el siglo XIX conviven dos tipos de fortepianos. Los de
mecánica vienesa, conectaban directamente el macillo a la tecla mediante
una bisagra y poseían por tanto una acción ligera y de pequeño calado. En
los de mecánica inglesa, en cambio, el macillo estaba atado al instrumento,
y una serie de palancas, permitía multiplicar la velocidad del macillo,
mientras que la tensión de las cuerdas implicaba un bastidor más sólido y
resistente
El camino que conduce hasta el moderno piano de concierto no es
más que un perfeccionamiento progresivo de la mecánica inglesa, unido al
mecanismo de doble repetición inventado por Sebastián Erard, a mediados
del siglo XIX y que permite al macillo volver a percutir la cuerda antes de
que vuelva a su posición de reposo.
En el siglo XX, pocas modificaciones de relieve se han añadido al
diseño del piano, que esencialmente es el mismo de finales del XIX. Sin
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
2. ANÁLISIS DEL MECANISMO DEL PIANO
7
embargo a finales del siglo XX, aparece el “piano electrónico” al que
podríamos perfectamente designar como un nuevo instrumento, dadas las
diferencias de mecánica, así como de generación del sonido. La idea del
sintetizador, que busca inicialmente la imitación, por síntesis digital, de los
instrumentos sinfónicos, pronto se visualiza como un camino potencial para
la búsqueda de nuevas sonoridades y nuevos medios de expresión. Sin
embargo, en lo que respecta concretamente a la imitación del sonido del
piano, queda aún mucho trabajo por hacer en este campo.
A la vista del rápido desarrollo de nuevos instrumentos basados en
generación digital del sonido, surge la tentación de especular sobre el
futuro de los instrumentos tradicionales. Es más que probable, que en el
futuro, conseguida ya una imitación perfecta del sonido y la mecánica del
piano, la mayor parte de la música se interprete con instrumentos
electrónicos, ya que pueden lograrse extrapolaciones a nuevos sonidos,
matices y niveles dinámicos, que no eran accesible por los originales, así
como resuelven el fastidioso problema de la afinación.
Es difícil deducir a priori, si los sonidos de piano pertenecen al grupo
de sonidos tradicionales que perdurarán frente a los sonidos de nueva
generación. No obstante, habida cuenta de la actual popularidad del piano y
de la lenta evolución en cuestión de gusto musical, es posible profetizar que
el sonido pianístico gozará de una salud envidiable al menos por otros 300
años.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
2. ANÁLISIS DEL MECANISMO DEL PIANO
8
2.2. Aspectos básicos de la acústica del piano
Mecánica básica
Las distintas piezas de la mecánica básica de la percusión de un
piano de concierto se muestran en la figura 2.1
Figura 2.1. Niveles horizontales en la construcción del piano
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
2. ANÁLISIS DEL MECANISMO DEL PIANO
9
El elemento productor del sonido es una cuerda de acero. Cada una
de las cuerdas se enrolla por uno de sus extremos alrededor de una clavija y
por el otro está sujeta a la armazón metálica gracias a unos clavos o puntas
de sujeción. Cercano a las puntas de sujeción se encuentra el puente
conectado a su vez a un amplio panel de madera llamado tabla de armonía
o tabla de resonancia. La altura del puente es ligeramente mayor que las
terminaciones metálicas, causando por tanto una presión hacia abajo en la
tabla de armonía.
Figura 2.2. Mecanismo básico del piano
La cuerda es golpeada por un macillo, que se eleva una vez pulsada
la tecla mediante un complicado sistema de palancas denominado acción
Figura 2.3. Detalle del mecanismo de la acción
El martillo o macillo golpea siempre en una posición cercana al
clavijero. Concretamente, llamando L a la longitud nominal de la cuerda y
d a la distancia del punto de colisión a la cuerda, la relación d/L suele
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
2. ANÁLISIS DEL MECANISMO DEL PIANO
10
oscilar entre 1/7 y 1/9. Reducir la distancia d generalmente proporciona un
tono débil, debido a que el primer armónico tendrá menos energía.
Aumentarla demasiado puede provocar un tono borroso y poco claro.
Generación del sonido
Cuando el macillo golpea la cuerda, ésta se deforma en el punto de
colisión apareciendo dos ondas en la cuerda, viajando en direcciones
opuestas. El frente de ondas resultante es un pulso, cuya anchura va
aumentando hasta que uno de los frentes de onda se refleja en la clavija
(que es la terminación más cercana al punto de colisión). Dado que el
clavijero puede considerarse como una terminación rígida, el coeficiente de
reflexión es negativo, lo que significa que la onda, se refleja hacia abajo,
invirtiendo el sentido de la perturbación y devolviendo el desplazamiento al
nivel de equilibrio. Por tanto el frente de ondas que se desplazaba
inicialmente hacia la izquierda se convierte ahora en la cola trasera de un
pulso de anchura fija. Cuando el pulso llega al puente sufre de nuevo una
reflexión y así sucesivamente.
La longitud de la cuerda, junto con la velocidad de propagación en el
medio determina el tiempo de ida y vuelta del pulso y por tanto el periodo
de la onda pulsante resultante del recorrido del pulso por la cuerda.
La velocidad de propagación del pulso en la cuerda queda
determinada por la tensión (a mayor tensión mayor velocidad) y la masa
por unidad de longitud (cuanto más ligera sea la cuerda mayor velocidad).
La frecuencia fundamental de la onda resultante o lo que es lo mismo la
frecuencia del tono percibido queda determinada pues la longitud de la
cuerda, su tensión y su densidad lineal. En particular, la longitud y
densidad suelen intercambiarse para reducir el tamaño del instrumento,
sobre todo en los bajos, que requerirían de una longitud excesiva (a menor
frecuencia, mayor periodo y por tanto mayor longitud). Por ello, con objeto
de disminuir la longitud, las cuerdas graves, también llamadas bordones, se
fabrican en acero hilado en cobre.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
2. ANÁLISIS DEL MECANISMO DEL PIANO
11
Figura 2.4 Propagación del pulso inicial y Análisis espectral del pulso
viajero.
La onda formada por el pulso recorriendo la cuerda en toda su
longitud puede descomponerse en suma de los armónicos de la cuerda
vibrante. El armónico fundamental, cuya longitud de onda es el doble de la
longitud de la cuerda determina la frecuencia del tono percibido, mientras
que los armónicos secundarios proporcionan el timbre característico del
sonido del piano. En pianos reales, las frecuencias de resonancia de las
cuerdas no son exactamente armónicas, por lo que la relación entre los
armónicos no es proporcional. Esto significa que la vibración de la cuerda
no será completamente periódica conforme el tiempo avance, lo que
confiere una cualidad menos mecánica y más “viva” al sonido resultante
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
2. ANÁLISIS DEL MECANISMO DEL PIANO
12
Amplificación del sonido
Desafortunadamente, la cuerda vibrante por sí sola no puede generar
ningún sonido de forma eficaz y necesita por ello de un mecanismo
amplificador. Esto se consigue en un piano mediante la tabla armónica o
tabla de resonancia, que es un radiador mucho más eficiente del sonido y a
la que se conectan las cuerdas por medio del puente. Sin embargo, la tabla
de armonía es mucho más pesada que la cuerda, lo que significa que la
cuerda no podrá hacer vibrar a la tabla de resonancia y la energía seguirá
atrapada en la cuerda
En términos ingenieriles, existe una desadaptación de impedancias
entre la cuerda y la tabla. Desde el punto de vista de la cuerda, la tabla tiene
una gran impedancia de entrada, lo que significa que para adaptar
impedancias debemos incrementar la impedancia mecánica de la cuerda.
Esto puede lograrse haciendo la cuerda más pesada o bien incrementando la
tensión. En cualquier caso esto afecta a la rigidez y por tanto al timbre
deseado del piano. Por ello, la solución más común consiste en usar para
cada nota dos o tres cuerdas afinadas a la misma frecuencia (o casi),
aumentando así la energía transferida y por tanto el volumen sonoro
Sin embargo la amplificación sonora supone un sacrificio en la
duración del sonido. Ya sabemos que el pianista no puede suministrar
continuamente energía a la cuerda y por tanto la nota emitida está
condenada a extinguirse. Pero la velocidad de decaimiento está reñida con
la amplificación sonora, de modo que si ajustamos demasiado las
impedancias de la cuerda y la tabla de resonancia obtendremos un tono de
gran volumen sonoro pero de escasa duración, en cambio si usamos
cuerdas más ligeras y menos tensas, obtendremos un tono más duradero
pero de menor sonoridad.
Este compromiso entre duración y volumen es un difícil de conciliar,
ya que la impedancia de la tabla de resonancia puede variar bruscamente de
nota a nota.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
2. ANÁLISIS DEL MECANISMO DEL PIANO
13
2.3. Efectos de segundo orden
Rigidez no lineal del martillo
Volviendo a la excitación original de la cuerda por el golpe de
martillo, no solo la amplitud del pulso cambia con la fuerza del impacto,
sino también la forma del mismo. Esto significa que una nota en forte no
es solo la versión amplificada de una nota en piano. Esto tiene
consecuencias muy importantes en la síntesis digital del sonido de piano.
La razón de este efecto reside en una peculiaridad de los macillos
denominada rigidez no lineal. Esta característica consiste en que el
martillo, es sentido como un material suave por la cuerda cuando es
golpeada a un nivel dinámico pequeño (menor velocidad) y se transforma
en un material mucho más rígido cuando la cuerda es golpeada a gran
velocidad. Esta diferencia de rigidez en el martillo según el nivel dinámico,
hace que una nota en forte, genere un pulso inicial mucho más abrupto que
una nota en piano, por lo que la primera tendrá un componente espectral
mucho mayor que la segunda.
Figura 2.5. Diferencias en el espectro de los distintos niveles dinámicos.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
2. ANÁLISIS DEL MECANISMO DEL PIANO
14
Acoplamiento entre cuerdas
Otro efecto de segundo orden en la generación del tono en el piano
se obtiene por el hecho comentado anteriormente de la necesidad de usar
más de una cuerda por nota para lograr un compromiso adecuado entre
volumen y duración del tono.
En la figura, se muestra la función típica de decaimiento para un tono
de piano. La cuerda es golpeada aproximadamente en t = 2 y el apagador se
libera aproximadamente en t = 17 . Se observa claramente que la curva
puede dividirse en dos regiones. La región inicial, a la que podríamos
denominar tono transitorio, decae con mayor rapidez que en la segunda
región, que podríamos denominar tono permanente.
Figura 2.6. Nivel de Presión sonora frente al tiempo.
El comportamiento de la curva se explica mediante la existencia de
dos modos distintos de vibración, un modo con polarización vertical y otro
con horizontal. El modo polarizado verticalmente, es el principal modo
excitado por el martillo, así que comienza a una amplitud mucho mayor
que el horizontal. Sin embargo, dado que el puente, mediante el que se
conecta la cuerda a la tabla de resonancia, no opone tanta resistencia en la
dirección horizontal como en la vertical, el decaimiento del modo
verticalmente polarizado es mucho más rápido. Por tanto, una cantidad
relativamente apreciable de vibración horizontal se convierte, tras el
transitorio, en la componente dominante.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
2. ANÁLISIS DEL MECANISMO DEL PIANO
15
Sin embargo, el principal mecanismo en la generación de este tono
permanente, no es la existencia de estos dos modos, sino el acoplamiento
dinámico entre las 2 o 3 cuerdas golpeadas por el mismo martillo.
Para simplificar la cuestión, pensemos en dos cuerdas atadas al
mismo puente. Para estas cuerdas es posible vibrar en fase (modo
simétrico), o en oposición de fase (modo antisimétrico). En el caso
antisimétrico, las fuerzas ejercidas por el puente se cancelarán,
transmitiendo poca energía a la tabla de resonancia, con lo que el
decaimiento del tono será lento. En el caso simétrico, la fuerza en el puente
será mucho mayor que en el caso de una sola cuerda, así que la energía
transmitida a la tabla de resonancia será mayor así como la tasa de
decaimiento.
En la figura puede apreciarse la diferencia entre el decaimiento del
tono para una sola cuerda y para dos cuerdas acopladas. Puede verse
claramente, que un nuevo modo de vibración aparece, en el cual la cuerda
original puede vibrar por un tiempo mucho mayor antes de perder
totalmente su energía. Este es el modo denominado anteriormente como
antisimétrico.
Figura 2.7. Diferencias entre el decaimiento para una cuerda y dos cuerdas
conectadas al mismo puente.
Sin embargo, el modo en que el cerebro procesa los sonidos permite
tomar ventaja de esta situación. Un sonido es percibido como fuerte si
comienza fuerte, incluso aunque decaiga rápidamente y es percibido como
sostenido, incluso si es muy débil. Por tanto, un sonido que comience con
un volumen elevado transitorio y que decaiga rápidamente a un régimen
permanente de tono sostenido aunque débil, será percibido conjuntamente
como forte y sostenuto
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
2. ANÁLISIS DEL MECANISMO DEL PIANO
16
Inarmonicidad
Los armónicos del sonido de piano, no son exactamente múltiplos
enteros de la frecuencia fundamental. El espectro completo está algo más
expandido y la diferencia entre parciales es mayor que la frecuencia
fundamental. Típicamente, el décimo parcial toma la frecuencia del que
sería el undécimo en un caso totalmente armónico. En principio, puede
pensarse que esta inarmonicidad, es un factor a minimizar. Sin embargo,
contribuye a la formación del tono de piano y es un responsable principal
de su singularidad, añadiendo cierta “calidez” al sonido. Mediante
simulación, puede demostrarse que un piano sin inarmonicidad sonaría
artificial, por tanto será un factor a tener en cuenta a la hora de modelar el
sonido de piano.
Este fenómeno puede atribuirse a la rigidez inherente a las cuerdas
del piano, que produce una fuerza elástica que tiende a restaurar el estado
inicial oponiéndose a la perturbación. Esto lleva a la dispersión de las
ondas durante la propagación. La velocidad de fase de las ondas de alta
frecuencia es mayor que las de baja frecuencia y por tanto las frecuencias
más altas alcanzan el puente en un tiempo algo menor.
Considerando la ecuación de ondas de una cuerda rígida y sin
pérdidas:
2
4
∂2 y
2 ∂ y
2 ∂ y
=
c
−
K
∂t 2
∂x 2
∂t 4
(2.1) c =
T
ρ
K=
EI
ρ
I=
πd 0 4
64
(2.2)
Donde y es el desplazamiento transversal, x la posición a lo largo de
la cuerda, t el tiempo, c la velocidad de onda, K el coeficiente de rigidez, ρ
la masa lineal y T la tensión. E es el módulo de Young de la cuerda e I su
momento de inercia que depende del diámetro de la cuerda d 0 . Resolviendo
la ecuación de onda para rigidez pequeña (K<<1), se obtienen los
siguientes modos:
f n = nf 0 1 + Bn
2
para n>0
(2.3)
1 T
EIπ 2
f0 =
B=
2L ρ
TL2
Donde f 0 es la frecuencia fundamental, B el factor de inarmonicidad.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
(2.4)
2. ANÁLISIS DEL MECANISMO DEL PIANO
17
Puede verse por tanto, que el factor de inarmonicidad es proporcional
al diámetro de la cuerda (a su cuarta potencia). A mayor diámetro, la
cuerda tiene mayor rigidez, asemejándose cada vez más a una barra rígida.
Esta es otra razón por la cual, las cuerdas del registro grave se fabrican en
acero hilado en cobre, de forma helicoidal y no simplemente aumentando el
grosor de la cuerda.
El factor de inarmonicidad es también inversamente proporcional a
la longitud de la cuerda (a su cuadrado). Por tanto, los pianos de cola son
menos inarmónicos que los pianos verticales.
Al oído, los sonidos de piano parecen más inarmónicos en el registro
grave que en el agudo. Una de las razones es que las cuerdas graves
contienen más parciales que las agudas, permitiendo una mayor percepción
de la inarmonicidad. Otra razón es que el umbral de audición está cercano a
la inarmonicidad del piano en el rango agudo.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
2. ANÁLISIS DEL MECANISMO DEL PIANO
18
Modos resonantes en la tabla armónica
La tabla armónica, como todo cuerpo físico, exhibe unas frecuencias
o modos resonantes. El problema reside en que, al ser un elemento muy
grande, las frecuencias resonantes estarán en el rango de audición y por
tanto deben ser tenidas en cuenta a la hora de modelar el sonido del piano
En la siguiente figura, pueden verse los 4 primeros modos resonantes
para una tabla armónica típica
Figura 2.8. Modos resonantes en una tabla armónica.
Para visualizar el patrón de onda estacionaria, la tabla armónica se
cubre uniformemente con una mezcla de partículas finas y se conecta a un
vibrador. El vibrador se sintoniza lentamente hasta alcanzar una de las
frecuencias resonantes, momento en el cual se observará un incremento en
el nivel sonoro emitido por la tabla armónica. En ese momento las
partículas se acumularán en los nodos mientras que los vientres
permanecerán limpios.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
2. ANÁLISIS DEL MECANISMO DEL PIANO
19
La frecuencia del modo resonante más bajo suele estar en torno a los
50 Hz. En este modo, el centro de la tabla armónica vibra violentamente
(vientre) mientras que los bordes permanecen estáticos (nodos). La tabla
armónica pierde rápidamente su efectividad como elemento radiante y
amplificador del sonido a frecuencias por debajo de las del primer modo
resonante, así que los tonos por debajo de 50 Hz no suelen tener mucha
energía en su primer armónico.
El patrón de vibración de la tabla armónica, con sus modos
resonantes, deberá tenerse en cuenta a la hora de modelar el sistema de
síntesis, especialmente en los modelos físicos, en los cuales se busca
simular el mecanismo físico de generación del sonido.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
3. AFINACIÓN DEL PIANO. INTRODUCCIÓN AL SISTEMA TEMPERADO
20
3. Afinación del piano. Introducción al sistema temperado
A la hora de diseñar nuestro modelo de síntesis, es necesario conocer
los fundamentos del fenómeno físico armónico y sus efectos sobre la
afinación del piano moderno. La relación en frecuencia entre los intervalos
más importantes así como entre semitonos consecutivos es de capital
importancia en la construcción de modelos de síntesis, en los cuales a
menudo se generan tonos secundarios a partir de un conjunto de tonos
básicos. Por tanto es necesario describir, aunque someramente, la estructura
matemática del sistema musical occidental y su aplicación práctica en la
afinación del piano.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
3. AFINACIÓN DEL PIANO. INTRODUCCIÓN AL SISTEMA TEMPERADO
21
3.1. Bases acústicas de la escala
En la Grecia antigua, los matemáticos sabían que las relaciones
interválicas más sencillas entre los sonidos corresponden con exactitud a
proporciones simples, expresadas en números enteros pequeños, entre las
longitudes de una cuerda vibrante. Si una cuerda pulsada que produce un
determinado sonido se acorta, por ejemplo, la mitad exacta de su longitud,
el sonido resultante es una octava más aguda que el original, suponiendo
que la tensión de la cuerda se mantiene constante. La misma cuerda
acortada sólo un tercio de su longitud, suena una quinta justa más aguda;
otras proporciones simples dan otros intervalos.
Los intervalos simples y las proporciones de longitud de la cuerda se
pueden comprobar con facilidad utilizando un monocordio, que en realidad
es una cuerda con un soporte fijo y el otro móvil, montado sobre una regla
apropiada. Si tomamos una cuerda de cualquier longitud (que supondremos
1 sin pérdida de generalidad) entre dos soportes fijos y la dividimos
mediante otro soporte situado entre ellos, podemos obtener las notas
representadas por la longitud
1
1
y 1 − , siendo n un número entero.
n
n
Figura 3.1. Monocordio para generar la serie armónica.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
3. AFINACIÓN DEL PIANO. INTRODUCCIÓN AL SISTEMA TEMPERADO
22
Supongamos que la cuerda sin dividir, de longitud 1, suena como el
Do-2 a dos octavas por debajo del Do-4 central del piano. Comprobaremos
que las longitudes de los segmentos mostrados en el diagrama anterior
sonarán de la siguiente manera:
Figura 3.2. Generación de los cuatro primeros armónicos de la nota Do-2.
El proceso de división no se puede prolongar demasiado sin llegar a
longitudes de la cuerda tan pequeñas que resultarían impracticables. Sin
embargo, suponiendo que podamos medirlas exactamente, las longitudes
darían los siguientes sonidos:
Figura 3.3. Serie armónica de Do.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
1
n
3. AFINACIÓN DEL PIANO. INTRODUCCIÓN AL SISTEMA TEMPERADO
23
Estos sonidos forman la llamada serie armónica de Do. Los números
son los ordinales de los armónicos en la serie. El número de cada sonido, es
también el denominador de la fracción que representa la longitud del
segmento de la cuerda que produce el sonido. El asterisco indica aquellos
sonidos que según los patrones musicales están demasiado desafinados, por
razones que pronto aclararemos.
Todos los sistemas naturales vibrantes generan armónicos. En
condiciones normales, una cuerda vibrante, no produce sólo el sonido
fundamental, sino que a la vez suenan todos los armónicos juntos. Los
armónicos sobre la fundamental están presentes en el sonido, pero con una
intensidad mucho más débil que la fundamental; su fuerza relativa decrece
cuanto más alto es el número del armónico, y en la mayoría de los casos, no
son audibles en absoluto más allá del decimosexto armónico.
La intensidad relativa de los armónicos sobre una fundamental
contribuye a nuestra percepción del timbre y de la individualidad
instrumental; la distribución de estas intensidades relativas da como
resultado una forma de onda característica. Un sonido puro, es decir una
fundamental sin armónicos, tiene una sonoridad clara y pobre como un
zumbido.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
3. AFINACIÓN DEL PIANO. INTRODUCCIÓN AL SISTEMA TEMPERADO
24
3.2. Proporciones interválicas
La serie de armónicos del ejemplo precedente consta de sonidos que
mantienen relaciones interválicas entre sí, pero estas relaciones permanecen
constantes sea cual sea la fundamental. Por ejemplo, los seis primeros
armónicos del Fa# bajo el Do-4 central son:
Figura 3.4. Primeros armónicos de Fa#.
Se puede comprobar con facilidad, experimentando con cuerdas de
diferente afinación, que la proporción de la longitud de la cuerda para
cualquier intervalo debe ser constante, suponiendo que la tensión y la
densidad de la cuerda permanezcan constantes.
En el plano frecuencial, podemos determinar que las frecuencias de
los sonidos de la escala corresponden logarítmicamente a números enteros.
Esto es bastante fácil de ver con la relación de octava. Si partimos de una
frecuencia f, su octava superior será 2f, la superior 2 2 f, la siguiente 2 3 f y
así sucesivamente. Estos coeficientes corresponden a los números de la
serie de armónicos.
Para el intervalo de octava más quinta justa, la relación en frecuencia
sería 1:3 es decir, 3f. El sonido a dos octavas por encima sería 2 2 ·3f y así
sucesivamente. El principio que se desprende es que cuando se suman
intervalos, sus proporciones en frecuencia se multiplican. Esto es
comparable a un procedimiento logarítmico en base 2.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
3. AFINACIÓN DEL PIANO. INTRODUCCIÓN AL SISTEMA TEMPERADO
25
Esta propiedad sugiere que debería ser posible obtener sonidos que
no aparecen en la serie armónica de Do, y por tanto generar toda la escala
cromática en un ámbito dado. Por ejemplo, podríamos generar doce alturas
diferentes a partir del Do más grave del piano y afinar los sonidos con
quintas justas pitagóricas.
Figura 3.5. Serie de Quintas de Do.
Puesto que cada una de estas quintas tiene una relación de frecuencia
de
3
2
(lo que equivale a una longitud de cuerda de ), para sumar quintas
2
3
sucesivamente, tenemos que multiplicar la frecuencia más grave por
factores sucesivos de
3
. Los números del ejemplo son los multiplicadores
2
y el Do más grave es la frecuencia básica (que según el patrón internacional
de afinación es de 32.70 Hz). La serie de once quintas superpuestas
proporciona los doce sonidos de la escala cromática y acaba con el Mi#
agudo. Si afinamos las notas correspondientes en el piano con las
frecuencias indicadas, el resto es una cuestión sencilla, pues partiendo de
las notas afinadas basta añadir octavas hacia arriba o hacia abajo.
Por desgracia, este procedimiento da resultados muy poco
satisfactorios. Para ver el porqué, calculemos la frecuencia de la siguiente
quinta ascendente de la serie, el Si# agudo, que enarmónicamente
corresponde al Do más agudo del piano. Su frecuencia en relación con la
del Do más grave, a partir del procedimiento de las quintas sucesivas sería
12
⎛3⎞
⎜ ⎟ = 129,746 . Sin embargo, si consideramos que este Do está a siete
⎝2⎠
octavas sobre el Do más grave, su relación con la frecuencia inicial sería
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
3. AFINACIÓN DEL PIANO. INTRODUCCIÓN AL SISTEMA TEMPERADO
26
2 7 = 128 . Esto significa que el Si# obtenido afinando quintas ascendentes
desde el Do grave será algo más agudo que el Do obtenido afinando
octavas ascendentes. El cociente entre las dos alturas, expresada como la
proporción interválica 1.014 se llama coma pitagórica, que es algo más
pequeña que un cuarto de tono, pero fácilmente perceptible.
Una coma comparable no se podía haber evitado afinando los
sonidos mediante cuartas justas, como demuestra el ejemplo siguiente.
Figura 3.6. Serie de Cuartas de Do.
La proporción de la cuarta justa
4
multiplicada doce veces, da un
3
resultado algo menor que el de cinco octavas mediante un factor de 1.014,
12
4
al igual que en el caso precedente: ⎛⎜ ⎞⎟ = 31.569 2 5 = 32 y el Rebb final será
⎝3⎠
fastidiosamente más grave que el Do correspondiente.
Una pequeña investigación adicional bastará para descubrir que
ninguna de las proporciones que representan intervalos simples dará una
división de la octava libre de comas
Figura 3.7. Afinación por serie armónica y por quintas sucesivas.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
3. AFINACIÓN DEL PIANO. INTRODUCCIÓN AL SISTEMA TEMPERADO
En el primer caso el Mi se obtiene como
1 de
5
27
la longitud inicial lo
que significa una frecuencia 5 veces mayor. En el segundo caso el Mi se
4
3
obtiene tomando quintas sucesivas lo que supone ⎛⎜ ⎞⎟ = 5.0625
⎝2⎠
El resultado práctico de cualquiera de estas afinaciones es que las
notas más agudas en la superposición de intervalos repetidos están cada vez
más desafinadas. Las desigualdades derivadas de la multiplicación,
inherentes a las proporciones interválicas, se pueden comprobar en la
propia serie armónica.
La proporción de esta diferencia
81
, llamada coma sintónica, revela
80
un hecho sorprendente. En el caso de las otras comas, era evidente que
existía una diferencia de notación entre Si#, Rebb y Do, y podríamos haber
supuesto que estas diferencias de notación eran el resultado de las
diferencias naturales en el método empleado para generar las frecuencias.
En el caso de los dos Mi del ejemplo anterior, no existe esta diferencia de
notación, ambos son el mismo Mi.
Examinemos de nuevo la serie armónica. Una propiedad que
podemos advertir, es que los intervalos entre armónicos adyacentes se van
haciendo cada vez más pequeños (p.ej.
10
=1.1111 es más pequeño que
9
9
=1.125). Pero esto no es evidente en la notación. En el ejemplo, la
8
distancia entre Do y Re es una segunda mayor, al igual que entre Re y Mi.
Así existe una desigualdad entre la serie armónica que podemos
generar y la notación musical que hemos elegido para representarla. En
otras palabras, nuestro sistema familiar de notación no puede representar en
detalle las notas de la serie armónica, o al menos no todas las notas.
Sabemos que la notación musical que utilizamos, aunque complicada e
incómoda de aprender, es adecuada para representar la música de nuestra
experiencia habitual, y quizás resulte algo alarmante descubrir que está en
desacuerdo con la realidad acústica
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
3. AFINACIÓN DEL PIANO. INTRODUCCIÓN AL SISTEMA TEMPERADO
28
3.3. El sistema temperado
La respuesta a esta evidente contradicción la proporciona el
temperamento igual, inventado a principios del siglo XVII, pero que no
gozó de amplia difusión hasta la época de J.S.Bach (que contribuyó en gran
medida a popularizarlo). En el temperamento igual, la octava se divide en
doce intervalos de semitono exactamente iguales, lo que significa que cada
semitono de la octava, allí donde esté situado, está representado por una
proporción constante, a saber 12 2 = 1.05926 . La segunda mayor temperada
2
3
viene representada por 2 12 y la tercera menor 2 12 y así sucesivamente a lo
largo de toda la escala cromática, de modo que la octava viene representada
12
por 2 12 =2.
El factor 12 2 es un número irracional y no puede expresarse como
fracción de dos enteros, por tanto, el semitono temperado no puede ser el
intervalo exacto entre ningún par de sonidos de la serie armónica (aunque
un valor muy aproximado es
18
)
17
Lo que esto significa es que de todos los intervalos de la escala
cromática temperada, sólo las octavas están afinadas con exactitud. Desde
el punto de vista de la afinación “ideal”, medida por la serie armónica, esto
es una desventaja general, desde el punto de vista de la interpretación y la
notación musical práctica, sin embargo, la ventaja es inmensa. Las comas
desaparecen y las diferencias de entonación entre los intervalos se dividen
por igual a lo largo de toda la escala y son demasiado pequeñas para ser
percibidas en la interpretación
En nuestro sistema de notación musical, su base diatónica permite un
subsistema den notas cromáticas con signos de sostenidos y bemoles, y que
el temperamento igual acomoda a la perfección esas notas cuando se
emplea la equivalencia enarmónica.
Un pequeño cálculo demuestra que la proporción de la quinta justa
7
temperada (siete semitonos) es 2 12 =1.498, ligeramente más pequeña que
1.5, la quinta pitagórica. La tercera mayor temperada es 1.2599, más
grande que la tercera mayor de la serie armónica 1.25. En definitiva, todos
los intervalos excepto la octava están imperceptiblemente desafinados.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
29
4. MODELOS DE SÍNTESIS
Podemos distinguir dos principales categorías de algoritmos de
síntesis: modelos de señal y modelos físicos. Los modelos de señal aspiran
a reconstruir el efecto sonoro perceptual sin analizar la fuente específica
que provoca el sonido, mientras que los modelos físicos buscan simular el
comportamiento de la fuente sonora.
El siguiente esquema muestra una posible clasificación de los
distintos tipos de modelos de síntesis
Modelos no lineales
Modelos de señal
Modelos lineales
Liberación de muestras
Modelos de síntesis
Diferencias finitas
Modelos físicos
Síntesis modal
Guiaonda digital
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
30
4.1. Modelos de señal
Los modelos de señal usan una descripción matemática del sonido.
Sus ventajas son la simplicidad y la fácil implementación. El problema de
estos modelos radica en el control del proceso de síntesis, sobre todo en lo
que se refiere a parámetros que intervienen en el discurso musical. De
modo que la mayoría de algoritmos se derivan heurísticamente y no
guardan relación alguna con el proceso real de generación del sonido, con
las consiguientes consecuencias negativas para la interpretación musical.
Esta es la razón por la cual es más difícil sintetizar sonidos
preexistentes como los de piano, que producir sonidos abstractos con los
modelos de señal, es decir, sonidos que nuestra percepción no puede
relacionar con un mecanismo de producción, o imaginar una fuente para
ellos. Es por ello que los modelos de señal se utilizan profusamente para la
generación de nuevos sonidos en música electrónica
Podemos distinguir básicamente tres tipos de modelos de señal:
métodos de síntesis global o no-lineales, métodos lineales o sinusoidales y
métodos de muestreo de forma de onda.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
31
4.1.1. Métodos de síntesis global
Los métodos de síntesis global persiguen el objetivo de generar el
sonido modelando una señal simple (una sinusoide, por ejemplo) usando
una función. Estos métodos son no-lineales ya que las operaciones
realizadas sobre la portadora no son simples adiciones o amplificaciones.
Este tipo de síntesis usa algoritmos relativamente simples con un pequeño
número de parámetros, pero el proceso de análisis es complicado. Es
generalmente difícil controlar la forma del sonido mediante estos métodos
dado que el timbre está relacionado con los parámetros de control de una
forma no-lineal.
Síntesis FM simple
Síntesis AFM
Modelos de síntesis global
Síntesis DFM
Síntesis PD
Otros modelos no-lineales
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
32
Síntesis FM
El ejemplo más conocido de síntesis global, es la modulación en
frecuencia o síntesis FM, expuesta originalmente por John Chowning en
1973. Este método de síntesis ha sido adaptado de la teoría de FM para
radiofrecuencia a la síntesis de audio.
A comienzo de los 80, la conocida marca de instrumentos musicales
Yamaha, presenta un método digital de síntesis de sonido denominado
Síntesis FM. El método de Yamaha estaba basado en los estudios de John
Chowning sobre esta materia y concretamente en su ensayo Síntesis de
espectros complejos de audio mediante Modulación en Frecuencia
publicado en 1973
En realidad, no era un enfoque totalmente nuevo, pues los métodos
de modulación en frecuencia, habían sido utilizados desde antaño por los
ingenieros de telecomunicación en la transmisión de señal, sobre todo en
aplicaciones de radio. El trabajo de Chowning era, sin embargo, la primera
aplicación práctica de estos conceptos en el ámbito del modelado digital de
audio.
La síntesis FM está basada, como su propio nombre indica, en la
modulación en frecuencia. La frecuencia de una onda determinada se
modula por otra onda de distinta frecuencia. El resultado contiene
elementos de ambas frecuencias junto con nuevos armónicos relacionados
matemáticamente con las frecuencias originales. Se puede demostrar
teóricamente que cualquier sonido, por complejo que sea, puede ser
modelado mediante una serie de modulaciones en frecuencia de ondas
senoidales.
Análisis FM
La ecuación general de la modulación FM es:
t
y (t ) = Ac cos(2πf c t + 2πk f ∫ m(τ )dτ )
(4.1)
o
Por tanto la frecuencia instantánea es:
f i (t ) = f c + k f m(t )
(4.2)
Lo que significa que la frecuencia instantánea de la señal modulada
oscila en torno a la frecuencia de portadora con una desviación máxima de
∆f = k f max m(t ) . Este parámetro recibe el nombre de desviación en
frecuencia.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
33
En la síntesis FM, la señal moduladora es siempre una señal senoidal
así que:
m(t ) = Am cos(2πf m t )
(4.3)
Introduciendo la moduladora dada por Ec. 4.3. en la ecuación de
análisis dada por la Ec. 4.2. tenemos que la ecuación de la síntesis FM es
t
y (t ) = Ac cos(2πf c t + 2πk f ∫ cos(2πf mτ )dτ = Ac cos(2πf c t + k f
o
Am
sin( 2πf mτ ))
fm
(4.4)
= Ac cos(2πf c t + β sin( 2πf mτ ))
Donde β , índice de modulación, se define como:
β=
∆f
fm
(4.5)
Ya que en este caso, la desviación de pico es ∆f = k f max m(t ) = k f Am
En la síntesis FM, la salida de un oscilador se aplica al control de
frecuencia de otro oscilador. El oscilador que controla la frecuencia es
denominado modulador, mientras que el oscilador que proporciona la señal
a controlar es denominado portador.
Figura 4.1. Diagrama de un sistema de síntesis FM
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
34
Si el modulador se sintoniza por debajo del nivel de frecuencia
audible (20 Hz aprox,), se tiene modulación FM sub-audio también
conocida como vibrato. La profundidad del vibrato se determina mediante
la amplitud de la onda moduladora.
Si por el contrario, el modulador se sintoniza por encima de 20 Hz,
frecuencias adicionales denominadas bandas laterales aparecen
simétricamente alrededor de la frecuencia de portadora.
Tanto las frecuencias exactas como la amplitud relativa de las bandas
laterales pueden determinarse usando tecnología digital controlando todos
los parámetros con precisión. La Síntesis FM clásica, también conocida
como Chowning FM, utiliza sólo ondas senoidales, resultando por tanto
una modulación lineal. Puede describirse analíticamente mediante la
ecuación:
y (t ) = A(t ) cos(2πf c t + β (t ) cos(2πf m t + φ m ) + φ c )
(4.6)
Donde A(t) es la envolvente en amplitud, f c es la frecuencia de
portadora, f m es la frecuencia moduladora y φm , φ c son constantes
arbitrarias de fase. La función β (t ) , denominada envolvente del índice de
modulación, determina el contenido armónico del sonido. Podemos
determinar la frecuencia instantánea del sonido sin más que derivar la fase:
1 d
1 d
(2πf c t + β (t ) cos(2πf m t + φ m ) + φ c )
θ (t ) =
2π dt
2π dt
1 dβ (t )
= f c − β (t ) f m sin(2πf m t + φ m ) +
cos(2πf m t + φ m )
2π dt
f i (t ) =
(4.7)
Determinar la relación precisa del índice de modulación β (t ) en el
contenido armónico requeriría de un análisis más preciso, sin embargo, es
posible obtener alguna información por simple inspección de la ecuación
anterior. La cantidad β (t ) f m multiplica una variación sinusoidal de la
frecuencia. Si β (t ) es constante, su derivada es cero, y por tanto desaparece
el último término, de modo que β (t ) proporciona la máxima desviación en
frecuencia con respecto a la frecuencia nominal de la portadora f c . Por
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
35
tanto si β (t ) es pequeño, se producen bajas frecuencias, por el contrario si
es grande pueden producirse armónicos de nivel alto. Dado que β (t ) es una
función del tiempo, el contenido armónico de la señal también puede
cambiar con el tiempo.
Normalmente tanto A(t) como β (t ) suelen ser constantes sobre un
gran intervalo temporal y dejan de serlo normalmente hacia el comienzo o
final del sonido para tener en cuenta efectos transitorios como
consecuencia del ataque de tecla.
Las bandas laterales poseerán armónicos parciales a las frecuencias
f c ± nf m .
Figura 4.2. Espectro de la señal Y(f)
En el caso de armónicos a frecuencias negativas, tendremos bandas
reflejadas, a la misma frecuencia en valor absoluto pero con un desfase de
180º. Cuando al reflejarse coinciden con otros armónicos parciales, la
cancelación parcial o total tiene un gran impacto en el timbre
Si f c y f m son ambos racionales, en una relación 1:N, el espectro
resultante será armónico pero sin incluir los parciales que sean múltiplos de
N. Por ejemplo para una relación 1:2, las frecuencias resultantes son f c ,
3 f c , 5 f c … Esta propiedad es muy útil para sintetizar instrumentos de
embocadura cilíndrica como el clarinete, los cuales se caracterizan por
incluir en el espectro sólo los armónicos impares del tono fundamental.
Si f c o f m son irracionales, entonces el espectro resultante será
inarmónico. El resultado para el oyente, que no será capaz de fundir los
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
36
sonidos en una resultante armónica se traduce una amplia paleta de timbres
brillantes y vibrantes, incluyendo tañidos de campana y similares. Estos
espectros inarmónicos, tienen al menos el doble de los componentes en
frecuencia de un espectro armónico, y en caso de bandas reflejadas pueden
obtenerse efectos de trémolos y de chorus
Figura 4.3. Ejemplo de espectro inarmónico creado por reflexión de
bandas laterales.
Para espectros armónicos, habrá usualmente implicada una
frecuencia fundamental, aunque no necesariamente ha de ser la frecuencia
de portadora. Para que sea así, f m debe ser mayor o igual que 2 f c , ya que
de este modo, todas las frecuencias negativas reflejadas serán superiores a
f c y ésta será considerada como el tono fundamental.
No obstante, el timbre percibido por el oyente no está determinado
solamente por las frecuencias presentes, sino también por sus amplitudes
relativas. Las bandas superior e inferior tienen amplitudes simétricas. La
amplitud de cada parcial se calcula en base al índice de modulación β (t )
que puede suponerse constante sobre el intervalo de tiempo sobre el que se
calcule el espectro β (t ) = β .
La amplitud de cada parcial f c ± nf m es J n ( β ) donde J n es la función
de Bessel de orden n, de modo que el espectro puede describirse
analíticamente por:
Y ( f ) = Ac
∞
∑J
n = −∞
n
( β )δ ( f c + nf m )
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
(4.8)
4. MODELOS DE SÍNTESIS
37
Lo que significa que en el dominio del tiempo, la ecuación de
síntesis puede escribirse como:
y (t ) = Ac
∞
∑J
n = −∞
n
( β ) sin((ω c + nω m )t )
(4.9)
Figura. 4.4. Funciones de Bessel de distinto orden
Para β =0, es decir sin modulación, la portadora tiene toda la energía
y no hay parciales. Conforme I aumenta, la portadora pierde fuerza y
aumenta la energía de los parciales. Una estimación de cuantos parciales
serán audibles para un valor dado de β es β +1, donde β se redondea al
entero más cercano. Los valores de la amplitud pueden ser negativos.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
38
Figura. 4.5. Ejemplo de bandas laterales para β =1
Figura 4.6. Ejemplo de bandas laterales para β =4
En general, conforme β aumenta, podemos inferir que mayor
cantidad de frecuencias serán audibles. Esto puede ser un verdadero
problema para síntesis digital, donde las bandas superiores podrían alcanzar
la frecuencia de Nyquist y producir aliasing. Dado que la señal FM no está
limitada en banda, la mayoría de sintetizadores digitales tienen un límite en
el máximo valor de β .
Uno de los inconvenientes de la síntesis FM es que la simetría lineal
en las amplitudes de las bandas superior e inferior. El oído humano
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
39
requiere más energía en las frecuencias inferiores para ser consideradas de
un determinado volumen que para frecuencias superiores. Por consiguiente,
la síntesis FM clásica parece estar sobrecargada en los agudos, y los bajos
suenan débiles. Esto puede subsanarse empleando técnicas más complejas
como la modulación previa de la moduladora o del propio índice de
modulación.
Mediante la técnica de síntesis FM pueden crearse espectros más
complejos sin más que aumentar el número de portadoras o de
moduladoras.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
40
Síntesis AFM
Como se dijo anteriormente, la simetría entre las bandas inferior y
superior de la síntesis FM clásica supone una limitación al grado de control
de la forma de la amplitud espectral deseada para la forma sintetizada.
Mediante una sencilla modificación en la ecuación de la síntesis FM clásica
podemos introducir cierta asimetría. Tomando de la ecuación Ec. 4.9.
y (t ) = Ac sin(ω c t + β sin(ω m t )) = Ac
∞
∑ Jn(β ) sin(ω t + nω
n = −∞
c
m
t)
Introducimos el un factor multiplicativo r n , sobre la amplitud de los
armónicos del espectro.
∞
∑r
n = −∞
n
J n ( β ) sin(ω c t + nω m t )
(4.10)
En la siguiente figura pueden verse las diferentes formas del espectro
para valores de r de 0.4 a 4.
Figura 4.7. Envolventes del espectro AFM para distintos valores de r
Puede verse, que conforme r aumenta, la envolvente del espectro se
desplaza hacia la derecha, lo que explica la ventaja de la síntesis AFM
sobre la FM convencional. El pico de la envolvente coincide con la
frecuencia de portadora cuando r alcanza el valor 1, ya que en este caso
AFM coincide con FM.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
41
Dos Portadoras
Además del espectro general, otra característica muy importante del
sonido es la presencia de formantes. Los formantes describen ciertas
regiones del espectro donde tienen lugar resonancias fuertes y pueden
localizarse como picos en la envolvente del espectro.
En la síntesis FM, los picos en la envolvente espectral pueden
controlarse usando un oscilador de portadora adicional. En el caso de un
único oscilador, el espectro generado estará centrado en torno a una
frecuencia formante. Cuando se añaden dos señales, sus espectros pueden
combinarse. Si el mismo oscilador se usa para modular ambas portadoras
(aunque usando distinto índice de modulación), y las frecuencia del
segundo oscilador es múltiplo entero de la del primero, el espectro de
ambas señales puede combinarse de modo que solapen las componentes
creándose un pico formante en la frecuencia del segundo oscilador.
En la figura, ambas portadoras son moduladas por el mismo
oscilador con frecuencia f m . El índice de modulación para la primera y
segunda portadora es β 1 β 2 . El valor β 2 es normalmente menor que β 1 , de
modo que el cociente β 2 / β 1 es pequeño y el espectro no se extiende más
allá de la región del formante
La frecuencia de la segunda portadora f c 2 se elige de manera que sea
un armónico, es decir, múltiplo entero de la frecuencia fundamental f o (que
normalmente coincidirá con la frecuencia de la primer portadora f c1 ) y que
además esté lo más cercana posible a la deseada frecuencia formante f f .
f c 2 = nf o = int(
ff
fo
+ 0.5) f o
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
(4.11)
4. MODELOS DE SÍNTESIS
42
De esta manera aseguramos que la frecuencia de la segunda
portadora está armónicamente relacionada con la de la primera. Si f o varía,
la frecuencia de la segunda portadora permanecerá lo más cercana posible a
la deseada frecuencia formante f f y a la vez seguirá siendo un múltiplo
entero de f o .
Figura 4.8. Síntesis FM con dos portadoras para la obtención de
formantes.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
43
Dos Moduladoras
Así como puede aumentarse el número de portadoras, también puede
hacerlo el de moduladoras. Para conseguir una mayor variedad espectral, la
forma de onda moduladora puede consistir en la suma de varias sinusoides
Si la frecuencia de portadora es f c y las frecuencias moduladoras son
f m1 y f m 2 , el espectro resultante contendrá componentes de frecuencia en
los valores f c ± if m1 ± kf m 2 , con i,k enteros. Además existen múltiples
combinaciones de las parejas i,k que proporcionan la misma frecuencia, de
modo que la amplitud final será la resultante de todas las contribuciones a
esa frecuencia.
Los índices de modulación serán en general distintos para cada
componente, β 2 β 1 . La amplitud de la banda lateral Ai ,k viene dada por el
producto de las funciones Bessel:
Ai , k = J i ( β 1 ) J k ( β 2 )
(4.12)
Análogamente al caso de una moduladora simple, las frecuencias
negativas se reflejan con un cambio de signo en la amplitud que puede
contribuir a la cancelación total o parcial de ciertas componentes.
La DFM (Double Frequency Modulation) proporciona un método
alternativo de síntesis digital, en el que las frecuencias armónicas pueden
ser generadas a partir de dos frecuencias dadas y ofrece otra alternativa
para generar espectros asimétricos con menor coste computacional que
AFM.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
44
Síntesis FM para sonidos de piano.
Para sintetizar un sonido de piano, es necesario crear una señal con
armónicos que no sean múltiplos enteros de la frecuencia fundamental. El
índice de inarmonicidad del n-ésimo parcial del sonido de una nota del
piano f n , puede expresarse como, a partir de la ecuación Ec. 2.3. como
In =
fn
= 1 + Bn 2
nf 0
(4.13)
Donde B suele ser del orden de una centésima de semitono.
Usando una serie de términos moduladores, cada uno con un índice
de modulación relativamente pequeño, de manera que cada uno solo genere
una frecuencia en cada banda lateral pero en una frecuencia de modulación
que no esté armónicamente relacionada con la fundamental, podemos
sintetizar un sonido de piano.
Síntesis PD
Este modelo de síntesis fue usado ampliamente en los teclados Casio
que aparecieron a mediados de los 80 y superaba algunas limitaciones de
los sintetizadores Yamaha que usaban su modelo patentado de síntesis FM
La síntesis PD es en muchos aspectos similar a la síntesis FM, pero
las operaciones fundamentales realizadas en la forma de onda no son las
mismas. En concreto, la síntesis PD provoca una distorsión en la fase de la
onda portadora de forma periódica. En la síntesis FM, la frecuencia de la
onda portadora está modulada por otro oscilador. En el caso de PD, la
forma de onda no está modulada por otro oscilador, sino distorsionada por
algún tipo de algoritmo de forma de onda arbitraria como pueden ser ondas
cuadradas, triangulares, ruido blanco, etc.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
45
Otros métodos no lineales
Otro método basado en la distorsión no lineal de una señal de entrada
es el método Le Brun. Este consiste básicamente en implementar un
mapeado de la señal sinusoidal x(n) con una función arbitraria de distorsión
w. La función w es almacenada una tabla y es indexada con x(n) para
producir y(n) en el mismo rango [-1,1].
Los armónicos producidos pueden ser controlados usando
polinomios de Chebyshev como funciones de distorsión. De hecho,
utilizando polinomios de Chebyshev de orden n, se obtienen sinusoides
puras de frecuencia n. Por consiguiente, usando una combinación lineal de
polinomios de Chebyshev como funciones de distorsión, pueden controlarse
exactamente las amplitudes de los distintos armónicos. Además la señal
puede limitarse en banda evitando así el aliasing.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
46
4.1.2. Métodos lineales
Los modelos lineales como la síntesis aditiva o sustractiva tienen
como objetivo construir la señal usando representación en frecuencia,
buscando emular el proceso de la percepción humana que analiza las
señales de audio de acuerdo a sus contenidos espectrales. Una amplia gama
de sonidos pueden producirse usando estas técnicas, pero generalmente, un
gran número de parámetros es necesario para la descripción del sonido.
La linealidad de dichos modelos les confiere una gran versatilidad
aunque puede suponer un inconveniente para modelar sonidos de
naturaleza fuertemente no-lineal.
Síntesis aditiva
Síntesis granular
Modelos lineales
Síntesis SMS
Síntesis sustractiva
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
47
Síntesis aditiva
La síntesis aditiva es una de las más simples e intuitivas de estas
técnicas espectrales. Se basa en el Teorema de Fourier según el cual
cualquier forma de onda periódica puede ser modelada como suma de
sinusoides con distintas amplitudes y frecuencias. La síntesis aditiva fue de
las primeras técnicas de síntesis utilizadas en la elaboración de música
sintética. Uno de los primeros trabajos sobre el tema fue publicado por el
profesor James A. Moorer en la revista Computer Music Journal.
Este método persigue la construcción un tono complejo mediante la
suma de sonidos elementales, generalmente sinusoides moduladas en
amplitud y en frecuencia. Puede interpretarse como un método para
modelar el espectro variante en el tiempo de un tono mediante un conjunto
de líneas discretas en el dominio de la frecuencia. Se necesitan tres
funciones de control para cada oscilador sinusoidal: amplitud, frecuencia y
fase de cada componente. En muchos casos, la fase puede dejarse a un lado
y la señal de salida puede representarse como:
y ( n) =
M −1
∑ A (n) sin[2πF (n)]
k =0
k
k
(4.14)
Donde y es la señal de salida, M es el número de osciladores
sinusoidales, Ak (n) y Fk (n) son la amplitud variante en el tiempo del késimo parcial y su frecuencia respectivamente. Para sonidos periódicos o
cuasi-periódicos, estos componentes tienen frecuencias que son múltiplos
de una frecuencia fundamental. Mediante métodos de análisis de Fourier,
se puede descomponer el sonido a modelar en una suma de señales
sinusoidales. Las amplitudes y frecuencias necesarias pueden determinarse
usando la STFT de la señal original (Transformada de Fourier de corto
plazo)
Una ventaja de este método es la flexibilidad y el potencial para
modificaciones dinámicas del sonido. Pero su inconveniente es el alto
número de parámetros de control. Con objeto de evitar eso, se ha
desarrollado una técnica de síntesis aditiva de grupos. En esta técnica, los
parciales son agrupados en torno a una frecuencia común y a una
envolvente de amplitud. Estos parciales agrupados se combinan para
formar tablas de onda.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
48
Síntesis granular
Otra técnica de síntesis lineal es la síntesis granular. Se basa en
sintetizar sonidos a partir de pequeños elementos de señal en el dominio del
tiempo llamados sonidos atómicos o granos. Estos granos pueden tener una
duración comprendida entre un milisegundo y más de cien. Los métodos de
síntesis granular pueden ser clasificados en función de cómo los granos son
obtenidos.
En la síntesis granular asíncrona (AGS), los granos son dispersados
sobre una región en el dominio de la frecuencia denominada nube. Los
granos pueden tener formas de onda similares o diferentes. La forma de
onda puede ser una sinusoide enventanada, una señal muestreada o bien
obtenida mediante un modelo físico.
En la síntesis granular síncrona de Pitch (PSGS), los granos se
obtienen de la STFT de la señal original. La longitud de la ventana
rectangular usada en la STFT es el periodo del sonido sintetizado, y cada
grano corresponde por tanto a un periodo de la señal.
Esta técnica de síntesis se usa para conseguir efectos interesantes y
sonidos derivados pero no para sintetizar los propios sonidos de piano.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
49
Síntesis por modelado de espectro
La síntesis por modelado de espectro o SMS, es un método que
busca sintetizar el sonido añadiendo separadamente los componentes
deterministas y estocásticos. El componente determinista del sonido se
obtiene calculando en primer lugar la STFT de cada porción enventanada
de señal. A partir del espectro complejo obtenido por la STFT, los picos
prominentes y sus trayectorias se extraen mediante algoritmos complejos.
El componente estocástico se calcula restando la parte determinista a la
señal original en el dominio de la frecuencia.
Cualquier modelo de síntesis sonora da por supuestas ciertas
características de la forma sonora a sintetizar o del mecanismo de
generación del sonido. El sonido producido por instrumentos musicales
puede ser modelado por la suma de un conjunto de sinusoides a las que se
añade un ruido residual. La componente sinusoidal o determinística,
corresponde normalmente a los principales modos de vibración del sistema.
La componente de ruido representa la energía producida por el mecanismo
de excitación que no se transforma en vibraciones estacionarias o bien otro
tipo de componentes que no son de naturaleza sinusoidal y se modelan
como aleatorias por comodidad. En el caso de sonidos de piano, la
componente sinusoidal es el resultado de los principales modos de
vibración de la cuerda mientras que el ruido caracterizaría la percusión
violenta del martillo contra la cuerda, así como otros comportamientos nolineales del sistema resonante.
La componente determinista queda descrita por una suma de
componentes cuasi-sinusoidales (es decir, sinusoides cuya amplitud y
frecuencia varían de forma suave con respecto a su frecuencia nominal).
Cada sinusoide modela un componente de banda estrecha del sonido
original y queda descrito por una función de la amplitud y de la frecuencia.
La componente estocástica, es decir, el ruido, queda descrito
completamente por su densidad espectral de potencia que proporciona la
potencia de señal frente a la frecuencia. Para las señales estocásticas, no es
necesario tener en cuentas detalles de fase instantánea o valores exactos de
la magnitud.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
50
Por consiguiente el modelo completo del sistema puede expresarse
de forma analítica como:
N
s (t ) = ∑ An (t ) cos[θ n (t )] + e(t )
(4.15)
n =1
Donde An (t ) y θ n (t ) son la amplitud instantánea y la fase de la nésima sinuoside respectivamente, y e(t ) es la componente de ruido. El
modelo asume que las sinusoides son armónicos parciales estables del
sonido y que cada uno tiene un cambio suave de amplitud y frecuencia. La
fase instantánea puede derivarse a partir de la frecuencia instantánea como
t
θ n (t ) = ∫ ω n (τ )dτ
(4.16)
0
Donde ωn (τ ) es la frecuencia instantánea de la n-ésima sinusoide.
Para la señal e(t ) , ésta puede ser descrita como un ruido blanco filtrado.
t
e(t ) = ∫ h(t , τ )u (τ )dτ
(4.17)
0
Donde u (τ ) es el ruido blanco y h(t ,τ ) es la respuesta de un filtro
variante en tiempo. La integral representa la convolución de un ruido
blanco con un filtro con una frecuencia de corte determinada.
Este modelo tiene problemas con sonidos que incluyen parciales
ruidosos, como los producidos por el vibrato, donde la frecuencia nominal
no puede determinarse con exactitud. Debido a estos problemas, la
separación entre componente determinista y estocástica es normalmente
complicada, y la implementación de estos procesos debe ser lo
suficientemente flexible para incluir sonidos con estos problemas
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
51
El proceso de generación es parecido al de los codificadores híbridos
de voz que involucran predicción lineal. En la siguiente figura se muestra la
figura de un posible diagrama de implementación
Figura 4.9. Diagrama de implementación del proceso de análisis.
En primer lugar preparamos la próxima sección del sonido a analizar
multiplicando la forma de onda con una ventana de análisis apropiada. El
espectro se obtiene mediante la aplicación de la FFT y los picos
prominentes del espectro son detectados y utilizados en un algoritmo de
decisión que detecta la magnitud, frecuencia y fase de cada uno de los
parciales presentes en el sonido original. Cuando el sonido no es
completamente armónico, como en el caso de sonidos de piano, un paso
previo de detección de pitch puede mejorar el análisis usando la
información de la frecuencia fundamental para elegir el tamaño de la
ventana de análisis.
La componente estocástica de la trama analizada se calcula
generando en primer lugar la señal determinista mediante síntesis aditiva de
los distintos parciales, y luego sustrayéndola de la forma de onda original
en el dominio del tiempo. Esto es posible siempre y cuando haya
concordancia de fase en ambas formas de onda. La representación
estocástica se obtiene mediante un ajuste espectral del cual se obtienen los
parámetros más relevantes.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
52
Figura 4.10. Diagrama del proceso de síntesis.
En el diagrama superior, la señal determinista, es decir, las
componentes sinusoidales, se construyen a partir de la información de
magnitud y frecuencia para cada parcial mediante síntesis aditiva. Esto
puede ser implementado en el dominio del tiempo con el tradicional banco
de osciladores o bien en el dominio frecuencial utilizando en enfoque
basado en la FFT.
La señal estocástica sintetizada es el resultado de generar una señal
de ruido con las características espectrales obtenidas del módulo anterior.
Dicha señal puede generarse mediante síntesis substractiva que puede
implementarse en el dominio del tiempo mediante una convolución o en el
dominio de la frecuencia partiendo de un ruido blanco y coloreándolo
adecuadamente.
El bloque que recibe el nombre de transformaciones musicales
permite una representación de elementos musicales basados en el análisis.
Teóricamente, su objetivo es controlar todos los parámetros musicales
relevantes del sonido como forma espectral, vibrato, amplitud total y
evolución en frecuencia. Estos parámetros pueden ser extraídos,
modificados y reintroducidos en el sistema antes de que se complete la
síntesis sin perjuicio alguno del sonido resultante. Este proceso puede
implementarse de forma sencilla cuando la entrada es una nota aislada, en
este caso la parametrización musical puede ser bastante completa.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
53
Síntesis sustractiva
En la síntesis sustractiva, el proceso es el opuesto al utilizado en la
síntesis aditiva. El sonido se construye, eliminando componentes
indeseados a partir de un sonido inicial complejo como puede ser un ruido.
Este método esta íntimamente relacionado con la teoría de filtrado digital.
En su forma más básica, la síntesis sustractiva es un proceso muy
simple en el que intervienen tres elementos: generador, filtro y
amplificador. La fuente o generador puede ser cualquier tipo de sonido
pero suele usarse un ruido de banda ancha. El filtro colorea el ruido
adecuadamente y el amplificador controla el volumen del sonido. El
proceso completo puede emular la característica espectral de un
instrumento.
La síntesis fuente-resonador es un ejemplo de este tipo de síntesis.
Una excitación de banda ancha es filtrada usando filtros resonantes. Esta
aproximación corresponde a lo que sucede en muchos sistemas físicos,
asumiendo que no existe realimentación del resonador a la fuente. Para
modelar sonidos percusivos como el del piano, se suelen hacer dos
aproximaciones: primero, el cuerpo vibrante genera un sonido compuesto
de sinusoides con decaimiento exponencial, segundo, independencia entre
la fuente y los valores de frecuencia. Desde un punto de vista físico, las dos
partes del modelo pueden interpretarse de la siguiente manera: Las cuerdas,
que corresponden a la estructura vibrante son representadas por el filtro
resonante, y el martillo que es el excitador físico, es representado por una
señal de corta duración.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
54
4.1.3. Métodos de liberación de muestras
Los métodos de liberación de muestras son de los más utilizados en
pianos digitales comerciales. Consiste en reproducir un sonido que ha sido
previamente grabado. Estos métodos son muy precisos a la hora de
reproducir un sonido específico pero no es capaz de reproducir cambios en
las condiciones de ejecución pianística. Los pianos que implementan este
tipo de síntesis, almacenan tonos separados del instrumento en memoria y
los reproducen cuando la tecla es presionada. Varias muestras de una
misma nota son necesarias para simular la modificación del timbre con la
dinámica. Dado que este método requiere una gran cantidad de datos, solo
unos pocos segundos son grabados. Tras el ataque, la forma de onda se
reconstruye mediante repetición de la sección estacionaria del tono. Por
consiguiente la amplitud y la evolución del timbre deben simularse
mediante un generador de envolvente y un filtro variante con el tiempo.
Con objeto de minimizar el espacio en memoria, solo se almacenan notas
cada 3 ó 4 semitonos. El resto de tonos se obtienen mediante
desplazamiento del pitch o pitch shifting.
El inconveniente de estos métodos es que el sonido inmediato al
ataque de la tecla suena bastante artificial. Además las técnicas de
compresión utilizadas para almacenar tal cantidad de datos tienden a
degradar la calidad del sonido percibido. No obstante, muchos pianos de
gama alta utilizan esta técnica. El concepto es sencillo y la implementación
del algoritmo relativamente simple. El problema es que mediante esta
técnica se sintetizan las notas separadamente, lo que significa que
fenómenos físicos como la transferencia de energía entre cuerdas, o la
acción del doble escape a la hora de ejecutar notas repetidas no son tenidos
en cuenta. Este método ha sido implementado con éxito durante mucho
tiempo, ya que el pianista no puede actuar sobre el sonido una vez que la
tecla es golpeada, lo cual favorece bastante a esta filosofía de síntesis. Sin
embargo, dada su naturaleza estática, es incapaz de recrear esa interacción
tan profunda entre pianista e instrumento que crea su propio tono personal,
más allá de la simple recreación de un sonido invariable y carente de vida.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
55
Síntesis PCM o Wavetable
En la síntesis PCM o Wavetable (tabla de onda), los sonidos
muestreados se almacenan directamente tras un cuantificador PCM sin
ningún tipo de codificación, por lo que su tamaño en memoria es elevado.
De hecho, los sistemas que implementan síntesis PCM tienen como
parámetro más crítico el espacio en memoria y por tanto, todos los
esfuerzos de desarrollo en esta síntesis han tenido como objeto último
optimizar dicho espacio. No obstante, con el abaratamiento de los
dispositivos de memoria y las nuevas tecnologías, cada vez más reducidas,
de almacenamiento de memoria, éste suele ser un problema cada vez
menos importante, por lo que la síntesis PCM se ha impuesto sobre las
demás en la mayoría de modelos comerciales.
Repetición en Bucle y Generación de Envolvente
Una de las técnicas usadas en sintetizadores basados en tabla de onda
para ahorrar espacio en memoria, es el looping o repetición mediante bucle
de pequeños fragmentos muestreados del sonido de un piano.
Para el piano, el sonido puede ser modelado, como ya se discutió en
el análisis del mecanismo del piano, mediante dos secciones principales.
Un régimen transitorio inmediatamente posterior al ataque de la tecla y un
régimen permanente con un tono sostenido de menor volumen. En la
sección transitoria o parte inicial del sonido, la amplitud y las
características espectrales del sonido pueden cambiar muy rápidamente. En
la sección permanente, por el contrario, las características del sonido
poseen menos cambios de forma dinámica.
La figura muestra una forma de onda del sonido de un piano con las
secciones transitoria y permanente indicadas. En este ejemplo las
características espectrales de la forma de onda permanecen constantes a lo
largo de la sección permanente, mientras que la amplitud decrece a una tasa
aproximadamente constante. Este ejemplo no es realista, pues en pianos
auténticos, tanto las características espectrales como la amplitud continúan
cambiando durante toda la emisión del sonido.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
56
Figura 4.11. Secciones Permanente y Transitoria de un sonido de piano.
El looping o repetición en bucle se realiza a partir de un pequeño
segmento, típicamente dos periodos de la sección permanente con el fin de
ahorrar espacio en memoria, que suele ser el factor más limitante en los
instrumentos que implementan este tipo de síntesis.
Figura 4.12. Repetición en bucle de una muestra
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
57
Para simular el decaimiento de la amplitud de la señal, se utiliza un
filtro de ganancia variable con el tiempo. La envolvente de amplitud de un
sonido de piano, puede modelarse como un filtro de ganancia lineal a
trozos. El más usado es el modelo ADSR (Attack-Decay-Sustain-Release)
consistente en 4 trozos lineales correspondientes a la fase de Ataque,
Decaimiento, Sostenido, y Liberación.
Figura 4.13. Típica envolvente de amplitud ADSR.
La sección Attack o de ataque simula el efecto provocado por la
colisión del martillo con la cuerda. En esta sección tiene lugar un aumento
rápido de la amplitud a partir del nivel mínimo como consecuencia de la
generación del sonido. Las secciones Decay y Sustain, son ambas secciones
de decaimiento progresivo del tono de piano como consecuencia de las
pérdidas de energía producidas por la vibración del instrumento. La
diferencia entre ambas tiene como objeto separar la sección transitoria de la
permanente, ya que, como se vio en el capítulo 2, ambos sonidos son de
naturaleza muy diferente. En este sentido merece la pena comparar la
envolvente ADSR con la curva de presión sonora de la figura 2.6. en la
cual se muestra la diferencia de comportamientos en relación a los distintos
modos y al acoplamiento entre cuerdas.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
58
Figura 2.6. Presión sonora frente al tiempo para un tono de piano.
La sección Release, o de liberación, implementa el efecto de retirar
el dedo de la tecla o bien de bajar los apagadores, en caso de que el pedal
derecho estuviera accionado.
Figura 4.14. Envolvente ADSR aplicada a la forma de onda resultante.
Un sistema típico de síntesis por tabla de onda almacena datos
muestreados de la sección de ataque y de la sección permanente del sonido
de piano. El sonido inicial es reproducido solamente una vez, mientras que
el sonido permanente se repite mediante un bucle hasta que termina la nota.
La longitud de las secciones de Ataque y Decaimiento de la envolvente
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
59
generalmente son fijas para un instrumento concreto, mientras que las otras
suelen ser configurables por el usuario
Longitud de Bucle
La longitud del bucle, medida en número de muestras debe ser igual
a un número entero de periodos del tono fundamental del sonido
reproducido. En caso contrario se obtiene un indeseable desplazamiento del
pitch. En la práctica la longitud del segmento de bucle para un piano suele
ser de varios periodos con respecto a la frecuencia fundamental del tono
generado.
Edición de Muestras y Procesamiento
Existe un cierto número de procesos de edición y procesamiento de
las muestras para preparar los sonidos muestreados previo a su utilización
en un sistema de síntesis por tabla de onda.
En primer lugar, es necesario alinear los extremos del segmento de
muestra a repetir en bucle para que sean compatibles. Si la amplitud y la
pendiente de la forma de onda al comienzo del segmento no se corresponde
con la del final, aparecerá un ruido indeseable o glitch durante la
reproducción del bucle.
En segundo lugar, es necesario un procesamiento adicional para
comprimir el rango dinámico del sonido con el fin de mejorar la relación
señal/ruido. Esta relación está determinada por el tamaño de palabra
(número de bits por muestra) y por la amplitud de la señal digitalizada. Los
sonidos de piano alcanzan su amplitud de pico muy rápidamente y de
forma inmediata comienza a decaer lentamente. Como es sabido, la
sensibilidad del oído se ajusta dinámicamente al nivel de señal, así que
incluso para un tamaño de palabra pequeño, el nivel de ruido se enmascara
cuando el nivel de señal está cercano a la máxima amplitud. Sin embargo,
conforme el nivel de señal decae, el oído se vuelve más sensible y el nivel
de ruido parecerá incrementarse. Usar un gran tamaño de palabra de
memoria, reduce el ruido de cuantización pero aumenta también el espacio
a utilizar en memoria.
Por tanto, se utilizan técnicas de compresión para mejorar la relación
señal/ruido de cuantización que consisten en reducir el rango dinámico de
las muestras de sonido almacenadas en memoria. Los datos muestreados
son descomprimidos durante la reproducción para restaurar el rango
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
60
dinámico de la señal. Esto permite el uso de muestras con una longitud
menor de palabra de memoria. Existen diferentes técnicas de compresión
que pueden ser usadas para comprimir el rango dinámico de una señal.
Además existe un cierto efecto de compresión inherente en la técnica
del looping descrita anteriormente, ya que si el procesador y el convertidor
A/D usados en la reproducción tienen un rango dinámico mayor que el
disponible en memoria, la aplicación de una envolvente de decaimiento
tendrá un efecto similar a la descompresión mencionada en el párrafo
previo.
Desplazamiento del Pitch (Pitch Shifting)
Con el fin de optimizar el espacio en memoria disponible, los
sistemas de síntesis por tabla de onda utilizan técnicas de desplazamiento o
transposición del pitch, o frecuencia fundamental del tono, para generar
diferentes notas a partir de un único sonido muestreado. Por ejemplo, si una
célula de memoria contiene el sonido muestreado del Do central de un
piano, esta misma muestra puede usarse para generar Do# o Re, es decir
sonidos situados uno o dos semitonos sobre la nota muestreada.
El desplazamiento de pitch se consigue accediendo a la muestra
almacenada a diferentes tasas. Por ejemplo, si se reproducen las muestras
de una en una, secuencialmente obtendremos el pitch original, mientras que
si se reproducen de dos en dos, el pitch resultante tendrá una frecuencia
doble que la original y por tanto el sonido percibido será una octava
superior.
En el ejemplo anterior, el puntero que accede a memoria se
incrementa solo un número entero de muestras (de una en una, o de dos en
dos). Esto permite solamente un número limitado de desplazamientos en
memoria. En un caso más general, el puntero a memoria podría constar de
una parte entera y una parte fraccional y el incremento podría ser un
número fraccionario de muestras. El puntero a memoria se denomina a
menudo acumulador de fase, y el valor del incremento, incremento de fase.
Por ejemplo, si el valor del incremento de fase fuera de 0.5, el tono
decrementaría una octava. Para un incremento de fase de 12 2 (1.05946), la
frecuencia del tono se incrementaría en un semitono.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
61
Evidentemente, cuando el valor del incremento no es entero, el valor
deseado se encuentra entre dos muestras disponibles. En la figura se
representa un esquema simplificado de direccionamiento en el cual, tanto la
dirección como el valor del incremento tienen una parte entera y
fraccionaria de 4 bits. En el ejemplo, el valor del incremento es 1.5
muestras. Los sistemas más simples simplemente ignoran la parte
fraccional de la dirección cuando determinan el valor a enviar al
convertidor analógico digital. Un diagrama de un sistema simple puede
verse en la siguiente figura
Figura 4.15.
interpolación.
Esquemas
de
direccionamiento
para
sistemas
sin
Supongamos que la nota almacenada es Do. Para averiguar el tono
resultante de multiplicar la frecuencia por 1.5, calculamos en cuántos
semitonos hemos de aumentar la frecuencia original para lograr una
frecuencia 1.5 mayor.
(12 2 ) n = 1.5
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
62
Donde, tomando logaritmos y redondeando al entero más próximo,
se obtiene:
n=
log 1.5
log 12 2
= 7.01955 ≈ 7
Un aumento de 7 semitonos significa que la nota generada a partir
del Do inicial es Sol. En este caso se podría haber deducido directamente a
partir del incremento
3
que corresponde uno de los intervalos básicos, en
2
concreto al intervalo de quinta justa.
Sin embargo, los sistemas más sofisticados, pueden realizar algún
tipo de interpolación matemática entre los datos disponibles para obtener
un valor más adecuado a reproducir. La precisión en frecuencia será la
misma en ambos casos, pero la salida estará severamente distorsionada en
los sistemas que no usen interpolación
Figura. 4.16. Esquema de direccionamiento con interpolación
Existen diferentes algoritmos para interpolar entre dos valores de
muestras. El más simple es interpolación lineal, consistente en la media
ponderada de las dos muestras más cercanas, con la parte fraccional de la
dirección usada como constante de ponderación. Por ejemplo si el puntero
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
63
de dirección indica una dirección de (n + K ) , donde n es la parte entera y K
la fraccional, entonces el valor interpolado puede ser calculado como:
s (n + k ) = (1 − K ) s (n) + ( K ) s (n + 1)
(4.18)
Donde s(n) es la muestra n-ésima de la señal. Aunque pueden
utilizarse técnicas más sofisticadas de interpolación para reducir la
distorsión, éstas suelen ser costosas computacionalmente y no suelen
utilizarse más que en instrumentos de alta precisión.
Otra técnica utilizada para suavizar el desplazamiento del pitch es el
sobremuestreo (Oversampling). De esta forma, los datos interpolados
durante la reproducción estarán más cercanos al valor real, debido al
incremento en el número de puntos para representar la forma de onda.
Evidentemente, esto tiene un alto coste en términos de requerimientos en
memoria.
En muchos casos, la mejor aproximación consiste en utilizar
interpolación lineal combinada con varios grados de sobremuestreo en los
casos que sean necesarios. La interpolación lineal proporciona una
precisión razonable en la mayoría de los casos, mientras que para los tonos
que necesiten mayor precisión, como por ejemplo en los agudos, se emplea
sobremuestreo. El efecto combinado de ambos puede producir excelentes
resultados
Divisiones (Splits)
Cuando el pitch de un sonido muestreado se modifica mediante
desplazamiento, el timbre del sonido también se ve afectado. El efecto pasa
desapercibido para pequeños cambios en el pitch, del orden de unos pocos
semitonos. Pero para un gran desplazamiento del pitch, la distorsión es
considerable. Así que para obtener un sonido natural de piano, y cubrir el
rango completo del instrumento, es necesario tomar un número diferente de
muestras, de forma que cada una cubra un rango de notas. La
implementación resultante se conoce a menudo como instrumento
multimuestreado. Esta técnica puede concebirse como un teclado dividido
en distintos campos, con una nota representativa para cada campo. Cada
uno de estos campos se conoce como división o split
El término división en velocidad o Velocity Splits hace referencia al
uso de diferentes muestras para diferentes velocidades de nota (p, mf, f), de
forma que una muestra se utiliza para una nota particular cuando es tocada
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
64
suavemente (p), mientras que una muestra diferente se utiliza para la
misma nota si es tocada a gran dinámica (f). Esta técnica no suele utilizarse
en pianos de gama baja debido al coste en memoria, aunque se incluye en
casi todos los de la gama media y alta.
Ruido de Aliasing
Las técnicas de interpolación para desplazamiento del pitch descritas
anteriormente también pueden resultar en la introducción de ruido de
aliasing en el sonido del piano. La generación de ruido de aliasing, y no
solo la distorsión del timbre, puede también limitar la cantidad de
desplazamiento de pitch que puede aplicarse a un sonido muestreado. Los
sonidos ricos en contenido armónico a alta frecuencia (como los sonidos en
forte) tendrán generalmente más problemas con ruido de aliasing. Un
filtrado paso-bajo aplicado tras la interpolación puede ayudar a eliminar el
indeseado efecto del ruido de aliasing así como las técnicas de
sobremuestreo.
Multicapa (Layering )
El término Layering hace referencia a una técnica en la cual se
utilizan múltiples sonidos para cada nota. Se utiliza en pianos de gama alta
para generar sonidos de gran riqueza.
Filtrado digital
Como se mencionó previamente, el filtrado paso-bajo puede ser
utilizado para eliminar ruido generado durante el proceso de
desplazamiento de pitch. Existen también otras aplicaciones del filtrado
digital en la generación del timbre para mejorar el sonido resultante. En
estas aplicaciones, la implementación del filtro es polifónica, es decir, que
un filtro distinto es implementado para cada voz y que debe ser ajustable
dinámicamente en parámetros como su frecuencia de corte o su factor de
calidad
Como ya sabemos, para el sonido del piano, el carácter del tono
cambia drásticamente en función del nivel de amplitud, siendo muy
brillante en los tonos fuertes y más suave en los débiles. Esto puede
solucionarse con la técnica de división en velocidad comentada
anteriormente, pero también pueden usarse filtrado digital implementando
un filtro paso de baja con una frecuencia de corte que varíe en función de la
velocidad de la nota. Este filtro digital ajusta dinámicamente el espectro en
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
65
frecuencia de la señal resultante en función de la velocidad de la nota,
permitiendo una recreación muy eficaz de este efecto pianístico tan
importante.
Otra importante aplicación del filtrado digital es el suavizado de las
transiciones entre muestras. Como se comentó, las muestras almacenadas
llevan incorporado este suavizado haciendo corresponder las muestras
inicial y final de cada segmento. Sin embargo al realizar desplazamiento
del pitch, puede perderse esta correspondencia. Por ello suele utilizarse
algún tipo de filtrado para suavizar este efecto.
También en la técnica de división del teclado, en la frontera entre
divisiones, existen notas provenientes de diferentes muestras. Una de estas
muestras ha sido generada aumentando el pitch mientras que la otra puede
provenir de una disminución del pitch, y por tanto el timbre de cada nota
puede ser significativamente diferente. Este problema puede aliviarse,
empleando un filtro digital que use el número de nota para controlar las
características del filtro. Dichas características se diseñan para compensar
el desplazamiento del pitch asociado con la división del teclado en splits.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
66
4.2. Modelos físicos
Al contrario que los modelos de señal, que buscan modelar la señal
resultante, la principal característica de los modelos físicos es que
describen los sistemas de generación del sonido con respecto a su
comportamiento físico. Dichos sistemas pueden reconstruirse bien a partir
del conocimiento de las leyes físicas que gobiernan las partes vibrantes del
sistema y expresándolas como ecuaciones diferenciales, o bien
directamente a partir del comportamiento de la solución de la solución de
dichas ecuaciones.
Existen dos razones fundamentales para utilizar modelos físicos de
señal. Una es la comprensión del fenómeno físico involucrado en la
producción del sonido y otra es la síntesis misma del sonido. Pero si el
propósito es modelar un piano real y reproducir su tono lo más fielmente
posible, estas dos motivaciones están inexorablemente relacionadas y la
precisión del sonido sintetizado validará el diseño del modelo físico.
Los modelos físicos dan una respuesta realista a la interacción del
pianista, dado que los parámetros del modelo están directamente
relacionados con las características físicas del instrumento y por
consiguiente con la gesticulación del pianista. Estos modelos son
generalmente complicados y requieren un elevado coste computacional.
Un problema añadido del modelado físico es que, para cada
instrumento, se necesita un modelo completamente nuevo para producir un
sonido realista. Si los fabricantes quieren ofrecer una amplia variedad de
instrumentos, necesitan sistemas hardware más flexibles, como puede ser
un dispositivo de propósito general, es decir un ordenador, con los
consiguientes problemas de síntesis en tiempo real, debido a la gran
cantidad de parámetros a procesar.
Los músicos experimentados querrán tener control total sobre el
instrumento, para conseguir interpretaciones realmente expresivas, pero los
amateurs prefieren crear sonidos convincentes sin necesidad de años de
práctica. Este problema limita por ahora el modelado físico a sintetizadores
especialitos más que a módulos de propósito general, panorama que puede
cambiar con la creciente velocidad de crecimiento de la potencia de los
procesadores.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
67
4.2.1. Método de diferencias finitas
El primer método usado en modelado físico estaba basado en
ecuaciones de diferencias finitas. El principio básico era obtener la
ecuación matemática que describe el movimiento vibratorio y resolverla en
un conjunto finito de puntos. La ecuación en diferencias finitas así obtenida
simula la propagación de las ondas en el sistema. Hiller y Ruiz son los
primeros en proponer el primer método de diferencias finitas para
propósitos de síntesis de sonido. Chaigne y Askenfelt, proponen uno de los
modelos más realistas de cuerda de piano percutida, combinando el trabajo
de Hiller y Ruiz con un modelo no-lineal de martillo. Un modelo más
completo de piano, tomando en consideración la tabla de armonía fue
presentado por Hikichi y Osaka.
Descripción del fenómeno sonoro
El piano es un ejemplo de cuerda golpeada de forma no lineal. La
descripción física es simple en el sentido de que sólo la velocidad del
martillo constituye una variable de control cuando la cuerda es golpeada,
puesto que el dedo que presiona la tecla no tiene conexión mecánica
significativa con el martillo una vez que éste es lanzado hacia la cuerda.
Este hecho es el responsable de que el sistema MIDI proporcione una
representación suficiente para describir la ejecución pianística, ya que la
dimensionalidad del control (dejando a un lado los pedales), se confina a un
grado de libertad por tecla, el parámetro velocidad.
Las cuerdas del piano, son uniformes, bastante tensas y con un
terminación casi rígida. Por tanto, se comportan de modo altamente lineal
bajo condiciones normales de ejecución. El modelo de guiaonda digital
para modelado de cuerdas resulta por tanto muy conveniente para una
cuerda de piano individual. Sin embargo, otros factores nada despreciables
como la rigidez de las cuerdas o el acoplamiento entre las mismas
incrementan el coste de la implementación. Menos importante es la
existencia de los dos modos de vibración longitudinal y transversal, así
como el acoplamiento entre todas las cuerdas cuando el pedal derecho está
activado.
Con el fin de simplificar el sistema, tomaremos inicialmente en
consideración solamente las vibraciones en el plano vertical para una sola
cuerda por tecla. Por supuesto, en un sistema de alta calidad, debe
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
68
implementarse el número apropiado de cuerdas dado que proporcionan
efectos sonoros importantes en el sonido pianístico.
La tabla de armonía y la caja de madera pueden considerarse
ampliamente lineales e invariantes en el tiempo. Sin embargo, al ser
grandes objetos vibrantes, poseen más modos resonantes en el rango de
audición que los objetos pequeños. Por tanto la propagación en la tabla de
armonía así como en el recubrimiento no puede confinarse a una sola
dimensión como en la cuerda.
A pesar de que sólo la velocidad es necesaria para especificar el
estado del martillo antes de golpear la cuerda, la colisión es altamente nolineal, debido a la rigidez no-lineal de los martillos, que ya se discutió en la
primera sección.
Ecuación de la cuerda vibrante
En la figura se muestra un esquema de la cuerda vibrante de un piano
Figura 4.17. Cuerda vibrante ideal
La ecuación de ondas para la cuerda vibrante ideal (sin pérdidas,
lineal y flexible) es:
Ky ′′ = ε&y&
(4.19)
Donde K es la tensión de la cuerda, ε es la densidad lineal de masa,
y es el desplazamiento de la cuerda desde su nivel de equilibrio y las
derivadas representan:
y = y (t , x)
y& =
∂
y (t , x)
∂t
y′ =
∂
y (t , x)
∂x
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
69
La ecuación de ondas Ec. (4.19), puede interpretarse a la luz de la
segunda ley de Newton F = ma , en una escala microscópica. Dado que
estamos interesados en las vibraciones transversales de la cuerda, la fuerza
recuperadora relevante (por unidad de longitud) viene dada por la fuerza
restauradora de los materiales elásticos, es decir, F = Ky ′′ . Es proporcional
a la tensión de la cuerda K y depende del desplazamiento con respecto al
nivel de equilibrio. Esta fuerza recuperadora es equilibrada en todos los
puntos por la fuerza inercial por unidad de longitud de la cuerda que viene
dada por la ley F = ε&y& , donde &y& no es más que la aceleración transversal y
ε la densidad de masa.
Para crear un modelo computacional a partir de una ecuación
diferencial, aplicamos la aproximación de diferencias finitas, mediante el
cual, la diferenciación se sustituye por una diferencia finita.
y& (t , x) ≈
y (t , x) − y (t − T , x)
T
(4.20) y ′(t , x) ≈
y (t , x) − y (t − T , x)
X
(4.21)
Donde T es el intervalo de muestreo temporal usado en la simulación
y X es el intervalo de muestreo espacial. Estas aproximaciones pueden
derivarse directamente de la definición de derivada parcial. Las
aproximaciones se vuelven exactas tomando límite cuando los intervalos de
muestreos tienden a cero. Para las derivadas de segundo orden, las
aproximaciones de diferencias finitas se definen como:
y (t + T , x) − 2 y (t , x) + y (t − T , x)
T2
y (t , x + X ) − 2 y (t , x) + y (t , x − X )
y ′′(t , x) ≈
X2
&y&(t , x) ≈
(4.22)
(4.23)
Sustituyendo la aproximación de diferencias finitas o FDA en la
ecuación de ondas se obtiene:
K
y (t + T , x) − 2 y (t , x) + y (t − T , x)
y (t , x + X ) − 2 y (t , x) + y (t , x − X )
=ε
2
X
T2
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
(4.24)
4. MODELOS DE SÍNTESIS
70
Que puede resolverse obteniendo una fórmula recursiva para el
desplazamiento de la cuerda y:
KT 2
y (t + T , x) =
[ y(t , x + X ) − 2 y(t , x) + y(t , x − X )] + 2 y(t , x) − y(t − T , x)
εX 2
En una implementación práctica, es común tomar T = 1 , X =
(4.25)
K
ε
T, y
evaluar la recursión en los enteros t = nT y x = mX para obtener la ecuación
en diferencias:
y (n + 1, m) = y (n, m + 1) + y (n, m − 1) − y (n − 1, m)
(4.26)
Por consiguiente, para actualizar los valores del desplazamiento de la
cuerda y (n + 1) , necesitamos los valores anteriores en los instantes n y
n − 1 , para cualquier punto m de la cuerda.
La adición a la ecuación de onda de términos correspondientes a
fenómenos de pérdidas y dispersión proporciona más términos de la forma
y (n − l , m − k ) . Estos términos pueden agruparse bajo una forma más general
∞
∞
∑∑α
k =0 l =0
k ,l
∂ k ∂ l y (t , x) ∞ ∞
∂ m ∂ n y (t , x)
= ∑∑ β m,n
∂t k ∂x l
∂t m ∂x n
m =0 n =0
(4.27)
Descomposición de onda viajera
La ecuación de ondas unidimensional Ky ′′ = ε&y& admite como solución
general:
x
x
y (t , x) = y r (t − ) + yl (t + )
c
c
(4.28)
que se conoce como solución de D’Alembert
x
c
Donde c = K ε es la velocidad de onda. yr (t − ) representa la onda
x
c
viajera desplazándose hacia la derecha mientras que yl (t + ) representa la
onda viajera desplazándose hacia la izquierda. Ambas funciones deben ser
doblemente diferenciables.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
71
Esta solución tiene la ventaja de que una función de dos variables
y (t , x) ha sido reemplazada por dos funciones de una sola variable en
unidades temporales, lo que reduce notablemente el cálculo computacional.
Además cada onda viajera satisface la ecuación de ondas ideal:
y r′ =
x
∂
x
−1 ∂
−1
y r (t − ) =
y r (t − ) =
y& r
c
c ∂t
∂x
c
c
∂
x 1∂
x 1
yl′ =
yl (t + ) =
yl (t − ) = y& l
∂x
c
c ∂t
c
c
2
1
⎛ 1⎞
y r′′ = ⎜ − ⎟ &y&r = 2 &y&r
c
⎝ c⎠
(4.29)
2
1
⎛1⎞
yl′′ = ⎜ ⎟ &y&l = 2 &y&l
c
⎝c⎠
(4.30)
Por lo que &y& = c 2 y ′′ para ambas ondas viajeras
Una solución para la ecuación de ondas de la cuerda vibrante puede
hallarse mediante una exponencial de la forma:
y (t , x) = e st +vx
(4.31)
Sustituyendo en la ecuación de onda Ec. 4.19. se obtiene:
Ky ′′ = Kv 2 y = ε&y& = εs 2 y
De donde
K
ε
=
s2
= c2
v2
(4.32)
Así que la solución puede escribirse como:
y (t , x) = e s (t ± x c )
(4.33)
Por superposición, una solución más completa es:
y (t , x) = ∑ A ( si )e si ( t − x / c ) + A − ( si )e si ( t + x / c )
+
(4.34)
i
Donde A+ ( si ) y A− ( si ) son funciones arbitrarias de variable compleja.
Tomando s = jw y extendiendo la suma a una integral, tenemos de nuevo la
solución D’Alembert.
x
x
y (t , x) = y r (t − ) + yl (t + )
c
c
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
(4.28)
4. MODELOS DE SÍNTESIS
72
4.2.2. Síntesis modal
La síntesis modal está basada en la premisa de que cualquier objeto
productor de sonido, puede ser representado como un conjunto de
subestructuras vibrantes, que quedan definidas por su caracterización
modal. Las subestructuras están acopladas entre sí y pueden responder a
excitaciones externas.
Este método es general dado que puede ser aplicado a estructuras de
complejidad arbitraria. Sin embargo, el coste computacional necesario, se
incrementa con rapidez al aumentar la complejidad del sistema lo que
impone serias aplicaciones prácticas a su implementación, sobre todo a la
hora de desarrollar instrumentos musicales en tiempo real.
La caracterización modal para una subestructura dada, consiste en las
frecuencias y los coeficientes de amortiguamiento de los modos resonantes
de la estructura así como la forma de cada uno de esos modos. Un modo
resonante se define esencialmente como un movimiento particular del
sistema en el que cada punto de la estructura vibra con la misma
frecuencia. Cualquier movimiento arbitrario de esa estructura puede ser
expresado como la suma de las contribuciones de cada uno de esos modos.
Los modos son excitados por una fuerza externa aplicada a un punto
dado de la estructura. La energía de excitación se distribuye entre los
modos según la forma de la excitación. Se asume normalmente que no
existe intercambio de energía alguno entre los modos. En la práctica, el
patrón de vibración resultante no puede ser completamente descrito por un
modo único, sino por la suma de infinitas contribuciones. No obstante, para
poder implementar la respuesta numéricamente, la estructura continua debe
ser dividida en un conjunto finito de puntos.
La caracterización modal puede ser obtenida analíticamente para
estructuras vibratorias simples, a partir de las ecuaciones diferenciales que
gobiernan su movimiento. Para estructuras complejas, el cálculo directo de
los datos no es posible y puede utilizarse un análisis basado en medidas
experimentales. Para una estructura mecánica dividida en N puntos, la
velocidad instantánea de cada punto puede calcularse en función de la
contribución de cada modo y de la fuerza externa ejercida. Conocidos
estos, puede calcularse la velocidad de cada punto del sistema lo que
proporciona la respuesta sonora buscada.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
73
4.2.3. Guiado digital de Onda
A partir del algoritmo Karplus-Strong (KS) se desarrolla el concepto
de Síntesis por Guiaonda Digital. Este algoritmo es una extensión de la
técnica de síntesis por tabla de onda, donde el contenido de dicha tabla
evoluciona con el tiempo. La tabla de onda cambia cada vez que una
muestra es leída. Un filtro paso de baja implementa el decaimiento del
tono.
Figura 4.18. Implementación del algoritmo KS
La función de transferencia del filtro es
H ( z) =
1
2(1 + z −1 )
(4.35)
Julius O. Smith ha extendido este algoritmo para desarrollar el
concepto de Síntesis de Guiaonda Digital. El enfoque mediante guiaonda
digital, proporciona eficientes modelos computacionales para síntesis de
sonidos de piano. Este método está relacionado con el de las diferencias
finitas pues ambos están basados en la discretización de la ecuación de
onda. La eficiencia de esta técnica reside en el hecho de concentrar todas
las pérdidas y dispersión de la estructura en un único punto (asumiendo que
el sistema es LTI). Las guiaondas digitales han sido desarrolladas
específicamente para síntesis de piano.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
74
Guiaonda digital
Una guiaonda digital se define como una línea de retardo
bidireccional de una cierta impedancia de onda R
Figura 4.19. Guiaonda digital. Una simulación muestreada de onda viajera
para ondas propagándose en cuerdas ideales.
Cada línea de retraso contiene una onda viajera acústica muestreada,
una viajando hacia la izquierda y otra hacia la derecha, ya que la vibración
de una cuerda ideal puede describirse como la suma de dos ondas viajeras
en diferentes direcciones. Esta línea de retraso bidireccional o guiaonda
digital puede modelar cualquier sistema acústico unidimensional, como
puede ser la cuerda de un piano. Por supuesto en cuerdas reales, el modelo
unidimensional debe incluir pérdidas y dispersión, lo que puede tomarse en
consideración mediante la inserción de filtrado.
Las variables físicas como presión, fuerza, velocidad…. , se obtienen
sumando componentes de onda viajera como se muestra en la figura:
Figura 4.20. Obtención de una señal física de una guiaonda digital usando
puntos de extracción.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
75
La magnitud física buscada se obtiene sumando las dos ondas
viajeras. Una onda viajera en sí misma no tiene significado físico al menos
que la señal en sentido opuesto sea nula. Las ondas viajeras son eficientes
para la simulación, pero no pueden medirse directamente en la realidad
física.
Modelado por guiaonda digital
Para transportar la solución de onda viajera al dominio digital es
necesario muestrear la amplitud de las ondas viajeras a una tasa de
f s = 1 / T muestras por segundo donde T es el periodo de muestreo. La
elección natural para el intervalo de muestreo espacial X es la distancia que
recorre el sonido en un periodo de muestreo T, X = cT . El muestreo se lleva
a cabo formalmente mediante el cambio de variables:
xm = mX
(4.36)
t n = nT
Sustituyendo en la solución de D’Alembert (4.28) tenemos:
y (t n , x m ) = y r (nT − mX / c) + y l (nT + mX / c) =
y r [(n − m)T ] + y l [(n + m)T ] = y + (n − m) + y − (n + m)
(4.37)
Donde hemos llamado y + (k ) = y r (kT ) , y − (k ) = yl (kT )
El término y + (n − m) puede interpretarse como el resultado de un
retraso de m muestras a la señal cuyo valor es y + (n) , mientras que el
término y − (n + m) puede verse como la señal de entrada a una línea de
retraso cuya salida es y − (n) . Esto lleva al siguiente esquema:
Figura 4.21. Simulación digital de una guiaonda sin pérdidas.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
76
Dado que y + (n) es la componente que viaja hacia la derecha, le
asignamos el rail superior. Análogamente ocurre para y − (n) . Nótese que la
posición a lo largo de la cuerda xm = mX = mCT está colocada de izquierda a
derecha en el diagrama, dando así una interpretación física a su
horizontalidad.
Finalmente, las ondas viajeras en ambos sentidos pueden sumarse
para generar una salida con significado físico de acuerdo a la fórmula:
y (t n , x m ) = y + (n − m) + y − (n + m)
(4.37)
Por tanto, podemos calcular el desplazamiento físico de la cuerda en
cualquier intervalo de muestreo xm mediante la simple suma de los raíles
superior e inferior, como puede verse en la figura en las posiciones x = 0 y
x = 3 X . El diagrama es similar a las estructuras de filtrado en escalera o
lattice, excepto por los retrasos en el raíl superior, la ausencia de uniones
de scattering, y la interpretación física directa. Para obtener un filtro en
escalera bastaría simplemente con introducir una terminación rígida en el
límite derecho y conmutar los retrasos del raíl superior al raíl inferior.
Cualquier guiaonda ideal unidimensional puede simularse de esta
forma. Es importante advertir que la simulación es exacta en los instantes
de muestreos, dentro de la precisión numérica de las muestras. Para evitar
el aliasing asociado al muestreo, se requiere que todas las formas de onda
que viajan sobre la cuerda sean inicialmente limitadas en banda a la mitad
de la frecuencia de muestreo. En otras palabras, el espectro de las
señales y r (t ) yl (t ) no debe exceder la frecuencia temporal de muestreo
f s = 1 T , así como las frecuencias espaciales no pueden exceder la mitad de
la frecuencia espacial de muestreo.
Un diagrama de simulación más compacto que permite representar
simulaciones de guiaondas tanto muestreadas como continuas se muestra
en la figura. La figura enfatiza que la guiaonda ideal sin pérdida es
simulada por una línea de retraso bidireccional, y que la interpolación
espacial limitada en banda puede usarse para obtener un resultado para una
posición x que no sea múltiplo de cT. La interpolación limitada en banda
sirve además para evaluar la forma de onda en un tiempo arbitrario que no
sea necesariamente un múltiplo de T
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
77
Figura 4.22. Diseño simplificado de la simulación de una guiaonda ideal
Idealmente, la interpolación limitada en banda se implementa
mediante la convolución de una función sampling sinc(x)= sin(πx) / πx con las
muestras de señal. Específicamente, para evaluar la señal en un tiempo
arbitrario t o , basta convolucionar la señal muestreada x(t n ) con la función
sinc [(t n − t o ) / T ] . Esta función es la respuesta impulsiva del filtro ideal cuya
frecuencia de corte es la mitad de la tasa de muestreo.
En la práctica, la función sinc de interpolación debe ser enventanada
a una duración finita. Lo que significa que el filtro paso bajo asociado
deberá exhibir una banda de transición en la que la respuesta frecuencial
pueda caer a cero a la mitad de la tasa de muestreo. La calidad de la
interpolación en la banda de paso puede ajustarse a la resolución del oído
humano eligiendo un producto ventana por ancho de banda de transición
suficientemente largo.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
78
Relación con la recursión en diferencias finitas
Puede demostrarse que la técnica de simulación por guiaonda digital
es equivalente a la recursión producida por el esquema de aproximación
por diferencias finitas aplicado a la ecuación de ondas que proporcionaba:
y (n + 1, m) = y (n, m + 1) + y (n, m − 1) − y (n − 1, m)
(4.26)
Para comparar esta ecuación con la descripción por guiaonda
sustituimos la descomposición en onda viajera
y (n + 1, m) = y + ((n + 1) − m) + y − ((n + 1) + m) =
= y (n, m + 1) + y (n, m − 1) − y (n − 1, m)
[
]
= y + (n − (m + 1)) + y − (n + (m + 1)) + y + (n − (m − 1)) + y − (n + (m − 1)) − y + (n − 1 − m) + y − (n − 1 + m) =
+
−
+
−
+
−
= y (n − m − 1) + y (n + m + 1) + y (n − m + 1) + y (n + m − 1) − y (n − m − 1) + y (n + m − 1) =
= y + (n − m + 1) + y − (n + m + 1)
= y (n + 1, m)
Luego observamos que efectivamente el resultado de la recursión
FDA es exacto en el caso sin pérdidas, pues es equivalente al método de
simulación por guiaonda digital, que es exacto en los instantes de muestreo.
La última identidad puede rescribirse como:
y (n + 1, m) = y + (n − m + 1) + y − (n + m + 1) =
= y + ((n + 1) − m) + y − ((n + 1) + m)
(4.27)
= y + (n − (m − 1)) + y − ((n + (m + 1))
Lo que significa que el desplazamiento de la cuerda en el tiempo
n + 1 , posición m , es la superposición de las ondas viajeras derecha e
izquierda en las posiciones m − 1 y m + 1 respectivamente en el tiempo n .
En otras palabras, la variable física puede calcularse para el siguiente
instante como la suma de las componentes de onda viajera a izquierda y
derecha.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
79
Ecuación de la cuerda vibrante con pérdidas
En cualquier cuerda vibrante real, hay pérdidas de energía debidas a
las terminaciones flexibles, rozamiento con el aire y fricción interna en la
cuerda. Aunque las pérdidas en los sólidos varían generalmente de un
modo complicado con la frecuencia, pueden aproximarse normalmente con
un pequeño número de términos aditivos en la ecuación de ondas. En el
caso más simple, la fuerza de rozamiento es directamente proporcional a la
velocidad transversal de la cuerda.
Ky ′′ = ε&y& + µy&
(4.28)
En este caso, las pérdidas son independientes de la frecuencia. Un
modelo más realista de aproximación de las pérdidas incluiría más
derivadas temporales de orden impar, proporcionando pérdidas
dependientes con la frecuencia.
Tomando y (t , x) = e st +vx en la ecuación de ondas, tenemos:
Ky ′′ = Kv 2 y = ε&y& + µy& = εs 2 y + µsy
v2 =
εs 2 + µs
v=±
K
=
ε
K
s 2 (1 +
Kv 2 = εs 2 + µs
(4.29)
µ
µ
s2
) = 2 (1 + )
εs c
εs
s
µ
(1 + )
c
εs
(4.30)
Donde c es la velocidad de onda en el caso sin pérdidas. Para altas
frecuencias (gran s ), o cuando el coeficiente de fricción µ es pequeño en
comparación con la densidad de masa ε , podemos aproximar
µ
1µ
(1 + ) 2 = 1 +
εs
2 εs
1
(4.31)
De modo, que para bajas pérdidas, obtenemos la siguiente relación
entre frecuencia temporal y espacial
1
µ
v ≈ ± (s + )
c
2ε
(4.32)
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
80
La solución de la ecuación de ondas es por tanto:
y (t , x) = e
st + vx
=e
st ± ( s +
µ x
)
2ε c
=e
x
µ x
s (t ± ) ±
c
2ε c
(4.33)
e
Las componentes de onda viajera a la derecha y a la izquierda son
−
µ x
2ε c
x
s (t − )
c
y e
respectivamente: e e
en la dirección de propagación.
µ x
2ε c
e
x
s (t + )
c
. Ambas decaen exponencialmente
Tomando s = jw , y usando superposición para construir formas
arbitrarias de onda, se obtiene la solución general en el dominio del tiempo:
y (t , x) = e
−
µ x
2ε c
µ x
x
x
y r (t − ) + e 2ε c yl (t + )
c
c
(4.34)
Muestreando ambas componentes en intervalos temporales de
separación T y espaciales de separación X=cT obtenemos:
y (t n , x m ) = e
=e
−
µmT
2ε
−
µ mX
2ε c
µ mX
y r (nT − mX / c) + e 2ε
y r [(n − m)T ] + e
µmT
2ε
c
y l (nT + mX / c) =
y l [(n + m)T ] =
(4.35)
= g m y + ( n − m) + g − m y − ( n + m)
−
µT
2ε
Donde g = e es el factor de pérdidas. El diagrama de simulación
para la guiaonda digital con pérdidas se obtiene directamente:
Figura 4.23. Simulación discreta de la guiaonda ideal con pérdidas.
Como en el caso sin pérdidas, la simulación en tiempo discreto de la
solución de onda viajera es una implementación exacta de la solución en
tiempo continuo en los instantes de muestreo. Es importante observar que
las pérdidas, que están distribuidas en la solución continua son
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
81
consolidadas o aglomeradas en posiciones discretas en la simulación. El
factor de pérdidas g, que resuma la pérdida distribuida actúa en un intervalo
de muestreo.
La aglomeración de las pérdidas distribuidas no introduce error de
aproximación alguno en los puntos de muestreo. Además, la interpolación
limitada en banda puede ofrecer reconstrucción precisa entre muestras, con
la única restricción de que todas las excitaciones iniciales estén limitadas
en banda a la mitad de la tasa de muestreo. Esta consolidación de las
pérdidas puede realizarse a mayor escala, de cara a reducir el coste
computacional, conmutando las pérdidas de las secciones internas y sin
observación de la guía de onda y consolidándolas en un número mínimo de
puntos. Dado que la simulación digital es lineal e invariante en el tiempo, el
diagrama de la figura 4.24. es exactamente equivalente al diagrama previo
de la figura 4.23.
Figura 4.24. Aglomeración de las pérdidas en los instantes de observación
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
82
Modelado del sistema completo
La tabla de armonía y el cuerpo del piano pueden modelarse
fácilmente en el sentido de que son componentes altamente lineales, e
invariantes en tiempo. Los problemas de implementación se derivan de su
gran tamaño, ya que los objetos vibrantes de grandes dimensiones tienen
generalmente mayor cantidad de modos resonantes en el rango de audición
humana que los objetos pequeños. Además la propagación de guiaonda en
el cuerpo del piano no está confinada a una dimensión como en la cuerda.
Esto significa que serían necesarias tres estructuras de guiaonda para
modelar la tabla de resonancia y el cuerpo del piano, lo que daría lugar a
modelos complejos y computacionalmente muy costosos. Esta dificultad
puede superarse incluyendo la respuesta compleja del elemento vibrante en
la propia excitación (modificada adecuadamente, claro está, por la colisión
martillo-cuerda). La misma técnica puede aplicarse igualmente a la
particularmente compleja aportación del número de cuerdas que vibran por
simpatía al presionar el pedal derecho o sostenuto. La conmutatividad de
estos elementos solo es posible debido a que poseen propiedades altamente
lineales.
El modelado del martillo resulta algo más complejo. A pesar de que
solo la velocidad es necesaria para especificar el estado inicial previo a la
colisión, sabemos ya que ésta es altamente no-lineal. Esta no-linealidad
proviene del fieltro que recubre el martillo, que al comprimirse actúa como
un muelle de constante elástica variable. Además, deben tenerse en cuenta
casos complejos como la posibilidad de que el martillo golpee la cuerda
una segunda vez antes de que la primera excitación haya desaparecido
completamente. Exceptuando al martillo, el resto del instrumento exhibe
características que pueden ser aproximadas satisfactoriamente usando un
modelo lineal.
La observación clave a la hora de modelar el instrumento es notar
que la interacción entre martillo y cuerda consiste esencialmente en unos
pocos eventos discretos para cada golpe de martillo siempre y cuando la
cuerda se encuentre inicialmente en reposo. Por tanto, la interacción
martillo-cuerda puede aproximarse mediante uno o pocos impulsos
discretos filtrados convenientemente para incluir la no-linealidad del
martillo.
Cuando el martillo golpea por primera vez la cuerda en reposo
encuentra una impedancia equivalente a una cuerda de longitud infinita.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
83
Por tanto, el pulso resultante de la colisión puede ser modelado como un
impulso unitario filtrado convenientemente. La perturbación se propaga en
ambas direcciones pero dado que el martillo golpea cerca del clavijero, la
onda reflejada en la clavija regresará al punto de colisión antes de que
tenga lugar cualquier otra interacción. Puesto que la onda reflejada es una
versión ligeramente filtrada del pulso original puede representarse también
por un impulso unitario filtrado. Este pulso secundario discurre sobre el
martillo. Si el martillo ya no está en contacto con la tecla no hay más
interacción y el pulso original es la excitación completa. Sin embargo, esto
no es lo usual debido a la cercanía del clavijero al punto de colisión, lo que
significa que se emitirá un nuevo pulso que viajará alejándose del punto de
colisión de una forma similar a la excitación original. En pianos reales, hay
generalmente dos o tres interacciones antes de que el martillo se separe de
la tecla, excepto para tonos muy agudos.
En gran medida, el número de impulsos generados viene
determinado por la cuerda que es golpeada. Por tanto, dado el número de la
cuerda y la velocidad del martillo, junto con la actual velocidad de cuerda,
se puede predecir de forma aceptable la amplitud y cronología de todos los
impulsos. Existe sin embargo una relativa imprecisión que ignoraremos en
relación con el hecho de que cuando el martillo golpea una cuerda que ya
está vibrando, el historial completo de la vibración de la cuerda interviene
en los detalles de la interacción martillo-cuerda. Afortunadamente, este es
un efecto de segundo orden que puede no ser deseable en la simulación.
Todo pianista ha observado alguna vez una nota inesperadamente brillante,
correspondiente quizá a la colisión de una cuerda vibrante cuando ésta se
aproxima al martillo, y que supone una ruptura de la continuidad dinámica
en el caso de un pianissimo. De modo que quizá supone una mejora el
hecho de eliminar la incertidumbre en la interacción martillo-cuerda. En
caso contrario, puede añadirse un grado adecuado de impredecibilidad
introduciendo perturbaciones aleatorias en los niveles del impulso de
colisión en función de la amplitud de las vibraciones previas al golpe de
martillo. De forma más precisa, la velocidad de la cuerda en el momento
del impacto v s puede usarse para corregir apropiadamente la amplitud del
impulso de colisión.
La amplitud de cada impulso de colisión determina la configuración
del filtro que convierte el impulso unitario en la forma de onda adecuada a
las condiciones dadas. Para el golpe inicial, el pulso puede calcularse
usando un modelo de martillo de piano golpeando una cuerda con
velocidad de colisión vc = v h − v s , donde vh denota la velocidad del martillo
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
84
y v s la velocidad de la cuerda. Por el momento, ignoraremos el estado
vibratorio de la cuerda previo a la colisión de modo que tomaremos v s = 0
y v h = vc .
Si el martillo fuera una masa puntual y la cuerda fuera una cuerda
ideal sin pérdidas, el pulso tendría una envolvente de decaimiento
exponencial y su amplitud sería una función lineal de la velocidad de
colisión. El fieltro no-lineal que envuelve al martillo da lugar a un pulso
que asciende y decae de forma parecida a la convolución de dos
exponenciales. Cuanto más fuerte es el golpe, es decir, cuanto mayor es la
velocidad de colisión, más estrecho y abrupto es el pulso resultante. Este es
el principal efecto de la no-linealidad del martillo y no puede ser ignorado
en la síntesis de sonidos de piano de alta calidad
El segundo pulso de colisión, si existe, es un poco más complicado.
En este caso, el martillo permanece en contacto cuando el primer eco del
golpe original regresa. Por consiguiente, tenemos una colisión entre un
martillo estático y un pulso de onda viajera en la cuerda. Si el martillo fuera
un elemento lineal, podríamos simplemente calcular los pulsos reflejados y
transmitidos a partir de la impedancia del martillo. Sin embargo, dado que
es un elemento no lineal, no puede usarse una descripción de impedancia y
debe calcularse el pulso reflejado numéricamente usando un modelo no
lineal.
El supuesto de velocidad inicial cero en la cuerda nos proporciona un
importante resultado: todos los impulsos tanto el primario como los
secundarios si existen, están predeterminados por la velocidad inicial de
colisión. Un ejemplo de la forma de onda resultante de la superposición de
los distintos pulsos puede observarse en la figura.
Figura 4.25. Impulsos inicial y secundarios
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
85
Tales formas de onda pueden aproximarse mediante impulsos
localizados en los picos y convolucionados con un filtro paso-baja que
proporcione la envolvente apropiada y que exhiba un decaimiento más
abrupto a mayor nivel dinámico.
Figura 4.26. Conformación del pulso mediante un Filtro Paso Bajo.
La entrada al filtro es una muestra aislada no nula, es decir, un
impulso unitario y la salida es el pulso de colisión deseado. Cuando la
amplitud de la entrada aumenta, el pulso de salida aumenta en amplitud y
disminuye en anchura, lo que significa que el filtro es no-lineal. Sin
embargo, para cada impulso específico el filtro opera como un filtro LTI.
De esta forma, el instrumento completo es linealizado con respecto a cada
velocidad de martillo posible.
En la figura se muestra un método para crear la forma de onda
mediante la suma de múltiples pulsos con sus niveles dinámicos
correspondientes.
Figura. 4.27. Creación del pulso de colisión múltiple.
Los diversos impulsos proporcionan respectivas respuestas
impulsivas que alimentan el sumador. El pulso de colisión resultante del
solapamiento de las distintas respuestas impulsivas alimenta el módulo que
simula el comportamiento de la cuerda.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
86
El diagrama del sistema completo de síntesis a priori se muestra en la
siguiente figura:
Figura 4.28. Diagrama de síntesis usando el orden natural de los
elementos.
Para un nivel dinámico específico, el modelo es totalmente LTI, lo
que significa que podemos conmutar sus elementos sin perjuicio del
resultado final. Por tanto, a fin de aliviar el coste computacional integramos
la respuesta de la tabla de armonía y el cuerpo del piano con el filtro que
modela la respuesta del martillo.
Figura 4.29. Diagrama de síntesis conmutado.
El resultado de la conmutación de los elementos sólo es válido para
una velocidad de colisión fija. Para diferentes velocidades de colisión,
simplemente hay que modificar convenientemente el filtro que engloba
tanto la respuesta del cuerpo del piano como del martillo. El modelo
funciona debido a que la no-linealidad fuerte del instrumento está
localizada únicamente en la colisión martillo-cuerda, y el resto de eventos
pueden ser modelados individualmente como elementos LTI en función de
la velocidad de colisión. Es importante notar, que si una cuerda es golpeada
antes de que el pulso de excitación finalice, la reproducción debe, o bien
terminar prematuramente, o bien calcular el solapamiento de las
excitaciones.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
87
En el caso más simple de una única colisión aislada, la estructura
final de síntesis se muestra en la siguiente figura
Figura 4.30. Diagrama de síntesis en el caso de interacción martillocuerda simple.
Dado que la reproducción de la excitación contenida en la tabla de
excitación debe ser accionada de algún modo, suele usarse la convención
de que al cambiar el valor de la velocidad de colisión, se accione la
reproducción de la excitación. El valor numérico de dicha velocidad,
también es usado para configurar los coeficientes de los filtros paso bajo
que proporcionan la envolvente y amplitud adecuada de la respuesta
impulsiva. Es aconsejable también añadir un escalado de salida, ya que
para obtener la máxima relación señal-ruido en un rango dinámico finito es
más conveniente escalar en amplitud la salida final, que la previa a algún
filtro digital recursivo. Sin embargo, este escalado distorsionaría la
amplitud relativa de una nota con respecto a la anterior que aún esté
sonando en la cuerda. Por esta razón, puede usarse escalado antes y
después del módulo que implementa la cuerda
Para el caso más complejo de tener en cuenta las sucesivas
interacciones por las ondas reflejadas en el clavijero, la estructura
resultante es:
Figura 4.31. Diagrama de síntesis con triple interacción y filtro
compartido.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
88
En este caso, se necesitan tres punteros diferentes para recorrer la
tabla de excitación, que implementan las 3 líneas de retardo de la figura
4.28. El disparo de la primera excitación ocurre cuando cambia el
parámetro v c , el segundo comienza tras un retardo fijo correspondiente al
tiempo de ida y vuelta desde el martillo al clavijero y el tercero comienza
tras el mismo retardo relativo al segundo. El filtro compartido paso bajo se
configura en función de la velocidad inicial de colisión. Compartir este
filtro corresponde a suponer que los sucesivos impulsos de interacción
secundarios son todos de la misma amplitud. Dado que esto no se
corresponde con la situación física real, un modelo más realista puede
obtenerse usando filtros separados.
Figura 4.32. Diagrama de síntesis con triple interacción y filtros
separados.
Con el fin de ahorrar coste computacional en el filtrado, y bajo la
hipótesis de cuerda inicialmente en reposo, podemos considerar que cada
pulso secundario es una versión suavizada del anterior y por tanto podemos
derivar la forma de onda final a partir de una única excitación y no de tres.
Figura 4.33. Diagrama de síntesis mejorado.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
89
En este caso cada filtro secundario necesita solamente suministrar el
efecto del recorrido de ida y vuelta del martillo al clavijero así como la leve
atenuación asociada con la reflexión en el punto de colisión. En este caso
además puede integrarse con el módulo de excitación para producir la señal
deseada
Dado que para la mayoría de las teclas, sólo se observan unas pocas
interacciones por colisión, este modelo computacional de piano alcanza un
gran nivel de realismo. El filtrado correspondiente al cuerpo del piano y a
la tabla de armonía han sido reemplazados por una tabla de valores y el
martillo por uno o varios filtros de bajo orden que convierten el impulso de
interacción en un pulso adecuado
El módulo que simula la acción de la cuerda del piano es el más
importante y ya fue objeto de discusión en apartados previos. Sin embargo,
para una cuerda de piano realista hay que añadir las terminaciones rígidas
que suponen el clavijero y el puente. El diagrama correspondiente se
muestra en la siguiente figura:
Figura 4.34. Diagrama del módulo simulador de la cuerda.
El pulso resultante de la interacción martillo-cuerda y proveniente
del módulo anterior se introduce en los raíles inferior y superior que
corresponden al conjunto de ondas viajeras a la izquierda y a la derecha
respectivamente. Una de las direcciones tiene un signo opuesto a la otra
para tener en cuenta la inversión provocada por la terminación de cuerda.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
90
Por la conmutatividad de los elementos LTI el diagrama anterior
puede simplificarse en la siguiente figura
Figura 4.35. Diagrama del módulo de cuerda simplificado.
En el nuevo diagrama, cada línea de retraso corresponde al tiempo de
recorrido en ambas direcciones en cada segmento de cuerda. La salida se
representa tomada a la mitad de la línea de retraso mayor, pero en realidad
puede tomarse en cualquier punto del bucle de realimentación. Sin más que
desplazar la primera línea de retardo a través del sumador a su izquierda
obtenemos el siguiente diagrama mucho más conveniente.
Figura 4.36. Diagrama alternativo
En este diagrama la entrada en el segundo sumador de f(t) está
factorizada en un filtrado en peine por separado. El retraso del filtro peine
contiene la diferencia de retardo entre las dos entradas en el diagrama
anterior y el retraso del bucle de realimentación es ahora suma de ambos
retardos. Esta factorización, facilita la posibilidad de implementar efectos
típicos que ofrecen los pianos comerciales como chorus o reverberación y
que no necesitan memoria extra dado que utilizan la que ya está disponible
para la simulación de la cuerda. Es también posible eliminar el filtrado
peine explícito sustituyendo la señal de entrada f(t) por su versión filtrada
g (t ) = f (t ) − f (t − τ ) , donde τ es el tiempo de ida y vuelta desde el punto de
colisión al clavijero. De este modo el módulo que sintetiza el efecto de la
cuerda consistiría simplemente en un bucle de retardo filtrado.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
4. MODELOS DE SÍNTESIS
91
Por supuesto, para síntesis de calidad, habría que emplear múltiples
bucles de retardo por cada nota. Cada bucle correspondería a una cuerda
diferente golpeada por el mismo martillo. Por consiguiente, en un
sintetizador comercial deberían existir al menos dos bucles de retardo,
desajustados levemente y excitados por el mismo pulso de colisión.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
5. EL SISTEMA MIDI
92
5. El Sistema MIDI
Los modelos de síntesis de sonido, simulan los mecanismos de
generación interna del sonido o bien los efectos sonoros que producen. En
este sentido, podemos decir que una vez analizadas las técnicas de síntesis
tenemos a nuestra disposición, los martillos, cuerdas, tablas armónica… en
definitiva todos los elementos que intervienen en la creación del sonido
Sin embargo existe aún otro elemento que separa al pianista de toda
la mecánica del instrumento y que a la vez la hace transparente,
ofreciéndole un interfaz que solo refleje las cuestiones relevantes para la
interpretación artística. Estamos hablando del teclado. Este elemento que
no se ha tenido en cuenta hasta ahora a la hora de sintetizar el instrumento,
cobra ahora singular importancia como medio de comunicación entre el
instrumentista y los mecanismos internos de creación sonora.
En un piano electrónico, esta función la realiza el sistema MIDI.
Independientemente de la técnica de síntesis utilizada, es necesario un
protocolo de comunicación para que los parámetros musicales (frecuencia
del tono, duración, dinámica…) sean introducidos en el sintetizador de una
forma que permita la ejecución pianística en tiempo real.
Dejando a un lado consideraciones de técnica pianística, como la
ineludible influencia del tacto y dureza de tecla así como del sistema
contrapesado del mecanismo de la acción interno al piano y de otras
cuestiones relacionadas con la dinámica muscular en la ejecución, el
sistema MIDI se presenta un modo eficaz de comunicación entre el pianista
y el instrumento y es especialmente adecuado para simular el modelo de
ejecución pianística pudiendo presentar un interfaz físico que recuerda en
muchos aspectos el teclado de un piano real.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
5. EL SISTEMA MIDI
93
5.1. Aspectos básicos
El protocolo de Interfaz Digital para Instrumentos Musicales o MIDI,
ha sido ampliamente aceptado y utilizado por músicos y compositores
desde su concepción en 1982. El protocolo MIDI proporciona un medio
estandarizado y eficiente de convertir información sobre una interpretación
pianística en datos electrónicos. La información MIDI se transmite en
mensajes MIDI, un conjunto de instrucciones que informa al sintetizador
que tipo de sonido debe generar. Este sintetizador generará el sonido
pianístico mediante uno de los métodos de síntesis mencionados
anteriormente (síntesis FM, liberación de muestras…). Por tanto, el
protocolo MIDI es transparente al medio físico de generación del sonido,
simplemente transporta los parámetros necesarios para generar dicho
sonido.
El flujo de datos MIDI es un flujo de bits unidireccional y asíncrono
a 31.25 Kbps. Con 10 bits transmitidos por byte (un bit de comienzo, 8 bits
de datos y un bit de parada). El interfaz en un instrumento MIDI incluye
generalmente tres conectores MIDI diferentes denominados IN, OUT y
THRU. El flujo de datos MIDI es originado por un controlador MIDI que
es el teclado del piano electrónico y es enviado en tiempo real al
sintetizador mediante el conector MIDI OUT.
El sintetizador o generador de sonido recibe los mensajes MIDI a
través de su conector MIDI IN, y responde a estos mensajes reproduciendo
los sonidos correspondientes. En la figura, se muestra un sistema MIDI
simple, consistente en un controlador de teclado MIDI y un módulo de
sonido MIDI. En los pianos electrónicos comerciales, el instrumento
incluye el controlador de teclado y el módulo de sonido MIDI en la misma
unidad. En estas unidades, existe por tanto un enlace interno entre el
teclado y el módulo de sonido. Muchos modelos permiten habilitar o
deshabilitar este enlace configurando la función “control local” del
instrumento.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
5. EL SISTEMA MIDI
94
Figura. 5.1. Un sistema MIDI simple
El canal físico MIDI se divide en 16 canales lógicos mediante la
inclusión de un parámetro número de canal de 4 bits en el mensaje MIDI.
Un instrumento electrónico de teclado puede generalmente transmitir en
cualquiera de estos 16 canales MIDI. Un módulo de sonido externo puede
configurarse para recibir en un canal MIDI específico.
La información recibida en el conector MIDI IN de un dispositivo
MIDI es repetida en los conectores MIDI THRU. Por tanto, pueden
encadenarse varios módulos de sonido conectando la salida THRU de un
dispositivo en el conector IN del siguiente dispositivo.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
5. EL SISTEMA MIDI
95
5.2. Mensajes MIDI
Un mensaje MIDI está compuesto de un byte de estado seguido
generalmente de uno o dos bytes de datos. Existen varios tipos de mensajes
MIDI. Al más alto nivel, los mensajes MIDI son clasificados en Mensajes
de Canal y Mensajes de Sistema. Los Mensajes de Canal son aquellos que
solicitan un canal específico y por tanto el número de canal está incluido en
el byte de estado. Los Mensajes de Sistema no hacen referencia a ningún
canal específico.
Los Mensajes de canal pueden ser además clasificados en Mensajes
de Canal de Voz o Mensajes de Modo. Los Mensajes de Canal de Voz
contienen los datos de la interpretación pianística y comprenden la mayoría
del tráfico en un flujo de datos MIDI típico. Los Mensajes de Modo afectan
al modo en que el generador de sonidos responderá a los Mensajes de Voz
de Canal.
Mensajes de Voz de Canal
Los mensajes de Voz de Canal son usados para enviar información
sobre la interpretación musical. Los mensajes en esta categoría son Note
On, Note Off, Polyphonic Key Pressure, Channel Pressure, Pitch Bend
Change, Program Change y Control Change.
Note On/ Note Off/ Velocity
En los sistemas MIDI, la activación de una nota particular y su
liberación son considerados como dos eventos diferentes. Cuando una tecla
es presionada en un piano electrónico MIDI, el teclado envía un mensaje
Note On o Nota activada por el puerto de salida MIDI OUT. El teclado
estará configurado para transmitir en alguno de los 16 canales lógicos
MIDI que estará indicado en el byte de estado para el mensaje de Note ON.
A este byte de estado le siguen otros dos bytes de datos, que especifican el
número de tecla (qué tecla ha sido pulsada) y la velocidad (velocidad con
que la tecla fue pulsada).
El parámetro Key Number o Número de Tecla es utilizado por el
generador de sonido para discriminar la nota que debe ser reproducida,
mientras que el parámetro Velocity o Velocidad es normalmente usado
para controlar la amplitud de la nota (teniendo en cuenta las variaciones
espectrales del timbre con la dinámica en los pianos de gama media y alta).
Cuando la tecla es liberada, el teclado envía un mensaje Note Off que
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
5. EL SISTEMA MIDI
96
también incluye dos bytes de datos para el número de tecla y la velocidad
con que la tecla fue liberada. Este último parámetro es normalmente
ignorado para sonidos pianísticos aunque puede ser no trivial para síntesis
de otro tipo de instrumentos musicales.
Program Change
El mensaje de Program Change o Cambio de Programa es usado
para especificar el tipo de instrumento que debería ser usado para
reproducir sonidos en un canal dado. Este mensaje necesita solo un byte de
datos que especifican el nuevo número de canal. Se utiliza en pianos
electrónicos que permiten reproducir distintos tipos de sonidos pianísticos
así como distintos instrumentos de teclado (clavicémbalo, órgano…)
Control Change
Los mensajes de Control Change o cambio de control son usados
para controlar una amplia gama de funciones del generador de sonido,
Como el resto de los mensajes de canal, solo afectan al número de canal
indicado en el byte de estados. En estos mensajes, el byte de estado es
seguido por un byte de datos indicando el número de controlador y un
segundo byte que especifica el valor de control. El número de controlador
identifica que función del generador de sonido será controlado por el
mensaje.
Bank Select
El número de controlador cero, se define como el selector de banco.
Esta función es usada en algunos sintetizadores, junto con el mensaje MIDI
de cambio de programa para aumentar el número de diferentes sonidos que
pueden ser seleccionados (puesto que dicho mensaje permite seleccionar
solamente entre 128 números de programa posibles).
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
5. EL SISTEMA MIDI
97
Mensajes de modo de Canal
Los mensajes de modo de canal (números de controlador MIDI 121 a
127) afectan al modo en que el generador de sonido responde a los datos
MIDI. El número de controlador 121 se usa para resetear todos los
controladores. El número 122 se usa para habilitar o deshabilitar el control
local (pudiendo desconectar el teclado del generador de sonido). Los
números de controlador del 124 al 127 son usados para seleccionar entre
los modos de operación: Omni Mode On/Off y Mono/Poly Mode.
Con el Omni Mode activado, el sintetizador responde a los datos
MIDI entrantes en todos los canales, cuando está desactivado, solo
responde al canal especificado en el parámetro número de canal. Cuando el
modo Poly esta seleccionado, los mensajes de Note On o Nota Activa son
reproducidos polifónicamente, lo que significa, que cuando se reciben
múltiples mensajes Note On, a cada nota se le asigna su propia voz. El
resultado es que múltiples notas pueden ser tocadas al mismo tiempo. Si se
selecciona el modo Mono, se asigna una sola voz a un canal concreto, de
modo que no pueden tocarse acordes, solo melodías lineales.
Los pianos comerciales traen ajustados por defecto el modo de
operación Omni On y Poly.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
5. EL SISTEMA MIDI
98
Mensajes de Sistema
Los mensajes de sistema se clasifican en mensajes comunes,
mensajes en tiempo real, o mensajes exclusivos. Los mensajes comunes de
sistema están pensados para todos los receptores en el sistema. Los
mensajes en tiempo real son utilizados para sincronización entre
componentes MIDI que requieran sincronismo. Los mensajes exclusivos de
sistema incluyen un código de identificación (ID) del fabricante y son
usados para transferir bytes de datos en el formato especificado por el
fabricante correspondiente.
Mensajes comunes de Sistema
Los mensajes comunes actualmente definidos incluyen MTC Quarter
Frame, Song Select, Song Position Pointer, Tune Request, y End Of
Exclusive”.
MTC Quarter Frame
El mensaje MTC Quarter Frame es parte del código MIDI de
información temporal, usado para sincronización del equipo MIDI con
otros dispositivos como cintas de audio o video.
Song Select
El mensaje Song Select se utiliza en secuenciadores MIDI que
pueden almacenar y reproducir un cierto número de canciones. Suele
utilizarse en pianos comerciales para almacenar canciones de muestra, que
puedan reproducirse con el fin de demostrar las cualidades tímbricas del
instrumento.
Song Position Pointer
El mensaje Song Position Pointer se utiliza para configurar el
secuenciador de forma que reproduzca la canción a partir de un instante
distinto del inicial. El desfase se indica en número de ciclos de reloj MIDI
y por tanto solo puede ser usado con equipamiento que posea sincronismo
MIDI, es decir, capaz de reconocer Mensajes MIDI de Tiempo Real.
Tune Request
El mensaje Tune Request se utiliza para configurar la frecuencia de
los osciladores de un sintetizador analógico. No se utiliza con
sintetizadores digitales.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
5. EL SISTEMA MIDI
99
EOX
El mensaje EOX se utiliza como flag de fin de mensaje, para los
mensajes exclusivos del sistema.
Mensajes de Sistema en tiempo real
Los mensajes MIDI System Real Time son usados para sincronizar
todos los dispositivos MIDI que dependan de una señal de reloj. La
mayoría de estos mensajes son normalmente ignorados por instrumentos de
teclado y sintetizadores. Para asegurar un sincronismo correcto, estos
mensajes tienen prioridad sobre otros, y pueden ocurrir en cualquier lugar
en un flujo de datos (p.ej., entre un byte de estado un byte de datos de algún
otro mensaje MIDI)
Los mensajes en tiempo real son Timing Clock, Start, Continue, Stop,
Active Sensing y System Reset.
Timing Clock
El mensaje Timing Clock es el reloj maestro que establece el tempo
de la reproducción de una secuencia. Este mensaje se envía 24 veces por
cuarto de nota.
Start, Continue y Stop
Los mensajes Start, Continue y Stop son usados para controlar la
reproducción de la secuencia.
Active Sensing
El Mensaje Active Sensing se utiliza para eliminar “notas atrapadas”
que pueden ocurrir si un cable MIDI es desconectado durante la
reproducción de una secuencia MIDI. Sin este mensaje, si se interrumpe la
conexión, algunas notas podrían reproducirse indefinidamente si se
recibiera un mensaje de Note On pero nunca se recibiera el correspondiente
mensaje de Note Off.
System Reset
El mensaje System Reset, se utiliza para resetear e inicializar
cualquier dispositivo que reciba el mensaje. Generalmente, este mensaje no
es enviado automáticamente, sino que debe ser iniciado manualmente por
el usuario.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
5. EL SISTEMA MIDI
100
Mensajes exclusivos de sistema
Los mensajes exclusivos de sistema pueden ser utilizados para enviar
datos como parámetros de ajusto, o datos de muestra entre dispositivos
MIDI. Los fabricantes de equipos MIDI definen su propio formato para
estos mensajes. Organismos como la MMA o el JMSC garantizan el
identificador único para un fabricante, ID que es incluido como parte del
mensaje. Dicha ID es seguida por un número indeterminado de bytes de
datos y la transmisión finaliza con un mensaje EOX.
Los fabricantes están obligados a publicar los detalles del formato de
los mensajes exclusivos del sistema, y otros fabricantes pueden utilizar
libremente estos formatos, a condición de que no alteren o utilicen el
formato en un modo que entren en conflicto con las especificaciones del
fabricante original.
Ciertos números de ID se reservan para protocolos especiales. Entre
estos, se encuentra el Standard MIDI Simple Dump que es un formato
definido en la especificación MIDI para la transmisión de datos entre
dispositivos MIDI .
Estado de Ejecución
Dado que los datos MIDI se transmiten en serie, es posible que los
eventos musicales que originalmente ocurrían al mismo tiempo y deben
insertarse en el flujo de datos MIDI, no sean reproducidos exactamente en
el mismo tiempo. Con una tasa de transmisión de 31.25 Kbps y 10 bits
transmitidos por cada byte de datos MIDI, un mensaje de “Note On” o de
“Note Off” de 3 bytes tardaría alrededor de 1 ms en transmitirse, lo cual es
suficientemente rápido para que los eventos se perciban como simultáneos.
Sin embargo, para un número mayor de acontecimientos
simultáneos, pudiera ocurrir que los retrasos introducidos por la
serialización de esta información llegaran a ser apreciables. Para reducir la
cantidad de datos transmitidos en el flujo MIDI, se emplea una técnica
denominada Running Status o Estado de Ejecución.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
5. EL SISTEMA MIDI
101
Esta técnica tiene en cuenta el siguiente hecho: es muy probable que
en una cadena de mensajes consecutivos, la mayoría sean del mismo tipo.
Por ejemplo, cuando se toca un acorde, 10 mensajes sucesivos de “Note
On” se generan, seguidos de 10 mensajes sucesivos de “Note Off”. Cuando
se utiliza el Running Status, un byte de estado es enviado por cada mensaje,
solo cuando el mensaje no es del mismo tipo que el último mensaje enviado
en el canal. Es decir, el byte de estado para mensajes subsiguientes del
mismo tipo son omitidos (solo los bytes de datos son enviados)
La efectividad de esta técnica puede acentuarse enviando mensajes
Note On con una velocidad cero en lugar de mensajes Note Off. En ese
caso, las cadenas contendrían solamente mensajes Note On de los cuales
sólo se enviaría el byte de estado para el primero de ellos.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
5. EL SISTEMA MIDI
102
5.3. Secuenciadores MIDI y Archivos MIDI
En un piano electrónico, los mensajes MIDI son recibidos y
procesados en un sintetizador MIDI en tiempo real. Cuando el sintetizador
recibe un mensaje MIDI de Note on, reproduce el sonido adecuado, y
cuando recibe el correspondiente mensaje Note Off, finaliza la
reproducción. Si la fuente del flujo MIDI es el teclado, entonces este flujo
de datos se genera en tiempo real, y no hay necesidad de enviar
información de sincronismo.
Sin embargo, la mayoría de pianos comerciales ofrecen la posibilidad
de grabar interpretaciones propias para reproducirlas posteriormente. Esto
significa, que los datos MIDI deben ser almacenados en un fichero para
poder editarse y reproducirse posteriormente por el secuenciador y, por
tanto, es necesario algún tipo de información cronológica para los mensajes
con el fin de reproducirlos en el orden adecuado. El estándar MIDI
proporciona un método para manejar este tipo de datos y un formato de
archivo estandarizado que permite no solo la reproducción posterior, sino
también la presentación multimedia en software especializado así como la
extracción de la partitura de una interpretación grabada.
La especificación para los ficheros MIDI estándar define tres
formatos. El Formato 0 almacena toda la secuencia de datos MIDI en una
pista única. El Formato 1 almacena la secuencia en una colección de pistas.
El Formato 2 puede almacenar varios patrones independientes. Este último
formato no se utiliza generalmente con secuenciadores MIDI para
aplicaciones musicales.
Los secuenciadotes MIDI más sofisticados manejan tanto el Formato
0 como el 1. Los ficheros MIDI 0 suelen ser más pequeños, y por
consiguiente reducen el tamaño en memoria y pueden ser transmitidos en
un menor ancho de banda. Sin embargo, los ficheros MIDI 1 pueden ser
visualizados y editados de forma más directa y por consiguiente son
preferidos para la edición de partituras.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
5. EL SISTEMA MIDI
103
Aspectos básicos del sintetizador
Polifonía
El término polifonía de un generador de sonido se refiere a la
habilidad de reproducir más de una nota al mismo tiempo. La polifonía se
especifica generalmente mediante el número de notas o voces. Inicialmente,
la mayoría de los sintetizadores eran monofónicos, lo que significa que
podían reproducir únicamente una nota a la vez. Los módulos actuales
suele oscilar entre 16, 24 o 32 notas de polifonía.
Sonidos
Los diferentes sonidos que un sintetizador puede generar son
llamados patches, programs o más genéricamente timbre. Los
sintetizadores programables pueden asignar números de programa a cada
sonido. Por ejemplo, el módulo de sonido de un piano comercial podría
usar el patch número 1 para sonidos de piano, el número 2 para
clavicémbalo, el número 3 para órgano… La asociación de cada número de
programa o “match” a cada sonido es a menudo denominada patch map
A través de MIDI, un mensaje de cambio de programa, puede
utilizarse para indicar el cambio de sonido usado a un dispositivo
recibiendo en un canal concreto
Modo Multitímbrico
Se entiende por sintetizador, o generador de sonido multitímbrico,
aquel capaz de producir dos o más sonidos de diferentes instrumentos
simultáneamente. En los pianos comerciales, existe la posibilidad de
separar el teclado en dos áreas, cada una de las cuales toca un instrumento
concreto (p.ej un bajo acústico en la región inferior y un sonido de piano en
la región superior). La polifonía de un sintetizador multitímbrico se asigna
dinámicamente entre los diferentes timbres usados.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
5. EL SISTEMA MIDI
104
5.4. Sistema General Midi(GM)
Al comienzo de cualquier secuencia MIDI, normalmente se envía un
mensaje de cambio de programa en cada canal usado en la secuencia para
configurar el sonido del instrumento apropiado para cada parte. El mensaje
de cambio de programa informa al sintetizador sobre el número de patch
para cada canal. Para que se reproduzcan los sonidos deseados, el match
map o asignación de números de match a sonidos debe ser la misma en
emisor y en receptor.
Anteriormente al desarrollo del sistema general MIDI, no existía un
estándar para la relación entre números de match y sonidos específicos. Por
consiguiente, una secuencia MIDI podría producir sonidos de diferentes
instrumentos al reproducirse en diferentes generadores. La especificación
general MIDI (GM) define un conjunto general de capacidades para
instrumentos MIDI típicos. El GM incluye la definición de un patch map.
Los canales 1-9 y 11-16 están reservados para instrumentos cromáticos,
mientras que el canal 10 se utiliza para instrumentos de percusión.
Para sonidos de instrumentos en los canales 1-9 y 11-16 el parámetro
número del mensaje Note On se utiliza para determinar la altura del sonido.
Para sonidos en el canal 10, este parámetro se utiliza para seleccionar el
sonido del instrumento de percusión a reproducir.
El GM especifica los sonidos usando los números de programa del 1
al 128. El mensaje de cambio de programa usa por tanto un 8 bits, lo que
proporciona un rango del 0 al 127, lo que significa que para seleccionar el
sonido número 10, tendremos que especificar el número de programa 9.
El GM especifica que instrumento o sonido corresponde con cada
número de programa, pero no especifica como son generados dichos
sonidos, ya que MIDI es sólo un protocolo de comunicación, no un método
de síntesis.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
6. EFECTOS DE SONIDOS COMUNES
105
6. Efectos de sonido comunes
En la mayoría de los pianos electrónicos comerciales de gama media
y alta, incluso en los instrumentos más elaborados orientados a una
interpretación musical seria podemos encontrar funciones que implementan
efectos de sonido que se añaden al sonido del instrumento. Estos efectos
pueden ser de origen natural, como la reverberación existente en cualquier
sala de conciertos o bien más artificiosos como los efectos típicos
denominados chorus o flanging por citar algunos.
En lo que respecta a la materia de este estudio, estos efectos suelen
implementarse en el mismo proceso de síntesis o bien en módulos
independientes que utilizan las mismas técnicas estudiadas en el capítulo 4
y es por ello que se incluyen en este trabajo.
Cuando se implementan en el mismo módulo generador de sonido,
los efectos se consiguen ajustando o modificando alguno de los parámetros
de síntesis, o bien, introduciendo un elemento perturbador, que
convenientemente ajustado, logre el efecto deseado. Cuando se
implementan como módulos independientes, como es el caso para los
pianos de gama media y alta, suelen utilizarse sobre todo modelos físicos,
ya que el análisis espectral necesario para sintetizarlos con modelos de
señal suele ser complicado, mientras que los mecanismos físicos que
intervienen en su gestación suelen ser de naturaleza sencilla y por tanto
fácilmente implementable.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
6. EFECTOS DE SONIDOS COMUNES
106
6.1. Reverberación
Aunque a priori un efecto de sonido pueda parecer un añadido
prescindible en el desarrollo de un instrumento electrónico, la
reverberación pertenece a la categoría de lo estrictamente necesario para
una interpretación musical de calidad.
La reverberación es un parámetro muy importante en la ejecución
musical. Basta como ejemplo advertir que las compañías discográficas y
los intérpretes recorren grandes distancias con el fin de encontrar el patrón
de reverberación más adecuado para la pieza a interpretar y que suele variar
enormemente de una sala de conciertos o auditorio a otro. De hecho, uno
de los grandes (y complejos) problemas a la hora de construir un espacio
adecuado para la interpretación musical es el problema de la acústica de
reverberación. Además, con la intervención de técnicas de amplificación
electrónicas (micrófonos, altavoces) la problemática, en lugar de
resolverse, se complica enormemente.
Es por ello que el efecto de reverberación no es un capricho gratuito,
sino que está muy ligado a la interpretación musical. Todo pianista conoce
de sobra el sonido tan seco que puede llegar a producir un piano en una sala
con condiciones de reverberación que no sean adecuadas. A veces, este
problema puede solucionarse haciendo uso del pedal de resonancia, pero
otras, este uso esta vedado por la naturaleza histórica de la pieza, o bien
provoca un emborronamiento armónico excesivo impide su utilización.
Todos estos problemas se solucionan añadiendo la reverberación adecuada
y absolutamente necesaria para una ejecución musical de calidad.
Consideremos en primer lugar los requerimientos para simular la
acústica de un auditorio. En principio, necesitamos solamente la respuesta
en uno o más puntos discretos del espacio, debida a una o más fuentes de
energía acústica. La propagación directa de señal desde la fuente del sonido
al sistema auditivo del oyente puede ser simulada usando una simple línea
de retraso en serie con un atenuador o un filtro paso de bajo como se
muestra en la siguiente figura:
Figura 6.1. Simulación de la propagación del sonido con pérdidas
independientes de la frecuencia.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
6. EFECTOS DE SONIDOS COMUNES
107
Si el sonido se atenúa conforme se propaga, con el mismo factor de
atenuación para cada frecuencia, la atenuación puede simularse con un
simple escalado de la salida. Este es otro ejemplo de la acumulación de
pérdidas distribuidas en puntos discretos, lo que significa que no es
necesaria implementar una pequeña atenuación para cada trayecto de
propagación sino que puede considerarse la atenuación del camino
completo.
Para un modelo acústico más preciso, es necesario tener en cuenta
atenuación dependiente de la frecuencia, reemplazando el factor constante
g, por un filtro digital G(z) como se muestra en la siguiente figura:
Figura 6.2. Simulación de la propagación del sonido con pérdidas
dependientes de la frecuencia.
En principio, un filtro LTI puede proporcionar un factor de
atenuación para cada frecuencia. Dicho filtro deberá satisfacer una
condición obvia: G (e jωT ) ≤ 1 .
En las figuras anteriores, la señal de entrada x(n) puede asociarse
con una fuente de señal y la salida y (n) con el punto de escucha. Si dicho
punto de escucha se encuentra a una distancia d con respecto a la fuente,
entonces la longitud de la línea de retraso M debe ser de:
M=
d
cT
Donde T representa el intervalo de muestreo. cT es la distancia que
el sonido se propaga en un intervalo de muestreo. Al dividir d entre cT
obtenemos cuántas muestras son necesarias para cubrir la distancia d. En la
práctica M se redondea al entero más cercano, lo cual no causa diferencias
audibles, a menos que el tiempo de eco sea demasiado corto. En este caso,
el sistema no percibiría el efecto realmente como un eco.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
6. EFECTOS DE SONIDOS COMUNES
108
En cuanto a la atenuación g, la teoría acústica nos dice que un punto
sonoro produce una onda esférica en un medio isotrópico como el aire. Por
tanto, el sonido de cualquier superficie radiante puede calcularse como la
suma de contribuciones de onda esférica desde cada punto en la superficie.
(principio de Huygens).
En una primera aproximación, la energía de la onda se conserva en
su propagación a través del aire. En una onda esférica de presión de radio r,
la energía del frente de onda se distribuye a lo largo de la superficie
esférica 4πr 2 . Por tanto, la energía por unidad de área de una onda esférica
decrece con radio 1 r 2 . Dado que la energía es proporcional al cuadrado
de la amplitud, una ley de inversa con el cuadrado para la energía se
traduce en una ley 1 r para la amplitud. Por tanto el factor de atenuación g
debe variar con la inversa de la distancia.
Sin embargo, la atenuación del sonido por la distribución esférica no
es la única fuente de pérdidas. En un modelo más realista deben tenerse en
cuenta las pérdidas por absorción. En medios como el aire, la absorción
varía con la frecuencia, donde las altas frecuencias suelen sufrir más
atenuación que las bajas. Asimismo, la propagación en cuerdas vibrantes
presenta una pérdida por absorción análoga.
Denotando g(r,w) el factor de pérdidas asociado a una distancia r a
una frecuencia w, bajo condiciones uniformes, la cantidad de atenuación es
proporcional a la distancia recorrida, lo que significa que los factores de
atenuación para dos segmentos de propagación consecutivos son
multiplicativos:
g (r1 + r2 , w) = g (r1 , w) g (r2 , w)
(6.1)
Esta propiedad implica que la atenuación g es una función
exponencial de la distancia r.
Además de la atenuación dependiente de la frecuencia, los filtros LTI
pueden proporcionar un retraso dependiente de la frecuencia.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
6. EFECTOS DE SONIDOS COMUNES
109
Reflexión y Reverberación
Cuando una onda esférica alcanza una pared o cualquier otro
obstáculo, puede sufrir reflexión o difracción. La reflexión tiene lugar
cuando el frente de ondas es localmente plano y por tanto la onda puede
considerarse como un rayo al que se le aplican las leyes de la reflexión
especular. La difracción tiene lugar cuando el frente de onda encuentra una
superficie con variaciones en la escala de la longitud de onda. La difracción
también se denomina reflexión difusa. Cada punto del objeto puede verse
como un nuevo emisor de ondas esféricas, sin embargo, al contrario de lo
que sucede en la reflexión especular, los hemisferios emitidos por cada
punto de la superficie no se combinan en un frente de onda organizado
La distinción entre reflexión difusa y especular es dependiente de la
frecuencia. Dado que el sonido viaja a una velocidad de unos 0.3 metros
por milisegundo, un cubo de 0.3 metros cúbicos causará reflexión especular
a sonidos por encima de 1KHz y difusa por debajo de 1 KHz. Una buena
sala de conciertos debe exhibir mayor reflexión difusa que especular. En
general, la reverberación debe ser difusa para evitar la formación de ondas
estacionarias, ya que deseamos extender la energía sonora uniformemente
en tiempo y espacio, sin que primen patrones temporales o espaciales
específicos, como ocurriría en caso de reflexión especular.
Supongamos ahora el caso más simple de eco acústico con dos
caminos de propagación.
Figura 6.3. Geometría de eco acústico causado por propagación
multitrayecto.
En la figura se muestra un sistema multitrayecto simple, donde S
representa la fuente acústica y L el oyente. Ambos están a la misma altura h
de una superficie reflectora. El camino directo tiene una distancia d
mientras que la longitud de la reflexión es 2r. Estas cantidades se
encuentran relacionadas por la ecuación
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
6. EFECTOS DE SONIDOS COMUNES
⎛d ⎞
r = h +⎜ ⎟
⎝2⎠
2
110
2
2
(6.2)
Este eco multitrayecto puede simularse de la siguiente forma:
Figura 6.4. Simulación digital del eco multitrayecto.
En la figura anterior no es necesario incluir ningún elemento común
que afecte igualmente a la señal directa y al eco, ya sea en retraso o
atenuación, ya que es la amplitud y desfase relativos de la señal directa con
respecto al eco lo que afecta al timbre. Teniendo en cuenta la geometría de
la figura, los parámetros pueden calcularse como:
M=
2r − d
cT
g=
1 2r d
=
1 d 2r
(6.3)
Podemos eliminar r haciendo uso de la ecuación (6.2) en su forma
de sustitución r = h 2 + (d 2)2 dejando solo dos variables independientes la
altura h de la fuente sobre la superficie reflectora y la distancia d entre la
fuente sonora y el oyente.
De una forma más general, una línea de retraso con múltiples tomas
puede simular reflexiones múltiples. Cada salida extrae el equivalente a una
reflexión y puede ser convenientemente filtrada para incluir la atenuación
por absorción y cualquier otro tipo de pérdidas.
Figura. 6.5. Línea de retraso con múltiples tomas.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
6. EFECTOS DE SONIDOS COMUNES
111
En principio este tipo de líneas de retardo pueden simular
eficientemente cualquier sistema reverberante, porque la reverberación
realmente consiste únicamente en la existencia de múltiples trayectos de
propagación acústica desde cada fuente. Sin embargo, la implementación
de estas líneas de retardo se vuelve computacionalmente muy costosa a la
hora de tener en cuenta todos los caminos posibles de propagación y aún
más cuando entran en juego fuentes u oyentes móviles
Modelo perceptual de reverberación
En la figura se muestra el escenario general de reverberación para
tres fuentes de sonido y un oyente (dos oídos).
Figura 6.6. Escenario general de reverberación para tres fuentes y un
oyente.
En general los filtros podrían incluir el filtrado realizado por el
pabellón auditivo, de forma que cada eco pueda percibirse con el ángulo
correcto de llegada en el espacio 3D, es decir, algunas reflexiones deberían
poder percibirse con sus direcciones naturales de propagación en el espacio
tridimensional.
Las dos señales de salida de la figura pueden calcularse mediante
seis convoluciones:
3
y i (n) = ∑ s j ∗ hij (n)
(6.4)
j =1
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
6. EFECTOS DE SONIDOS COMUNES
112
En música, un tiempo de reverberación típico es del orden de un
segundo. Para una tasa de muestreo de 60 KHz, cada filtro requeriría unas
50000 multiplicaciones y sumas por muestra lo que significa 2.5 billones
de operaciones por segundo. Para tres fuentes y dos puntos de escucha, se
alcanza la escalofriante suma de 30 billones de operaciones por segundo.
Esta cifra nos indica que la implementación exacta de funciones de
transferencia punto a punto en un espacio de reverberación es
computacionalmente muy compleja. Además debemos tener en cuenta de
que los filtros deben cambiar cuando alguno de las entidades se mueva.
Todo esto nos lleva a buscar un modelo computacional para el
espacio acústico completo, en lugar de modelos puntuales, en el que
fuentes y oyentes puedan moverse libremente sin afectar a la simulación
acústica. Esto lleva a la cuestión de cuales son los aspectos
perceptualmente importantes de la reverberación y como pueden simularse
con estructuras computacionales eficientes.
Se puede demostrar que para auditorios típicos, la densidad de eco
aumenta conforme al cuadrado del tiempo. Por tanto, tras una pequeña
respuesta transitoria inicial, la densidad de eco es tan grande que puede
modelarse mediante un proceso estocástico uniforme sin pérdida de
fidelidad perceptual. De forma similar, puede demostrarse, que el número
de modo resonantes en cualquier banda frecuencial aumenta también con el
cuadrado de la frecuencia de modo que a partir de ciertas frecuencias, la
distribución de los modos es tan densa que es perceptualmente equivalente
a una distribución estocástica de frecuencia con los parámetros adecuados
En definitiva, basándonos en los límites de la percepción humana, la
respuesta impulsiva de un espacio reverberante puede dividirse en dos
segmentos. El primer segmento, transitorio, denominado reflexiones
tempranas consiste en los primeros ecos dispersos en la respuesta impulsiva
que no forman un patrón homogéneo. En el segundo, denominado
reflexiones tardías, la densidad de los ecos es tal, que se impone una
caracterización estadística.
De la misma forma, la respuesta frecuencial de un sistema de
reverberación puede dividirse en 2 segmentos. El intervalo de baja
frecuencia consiste en una distribución de dispersa de modos resonantes,
mientras que a altas frecuencias los modos presentan una distribución tan
densa que pueden caracterizarse mediante una distribución estadística.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
6. EFECTOS DE SONIDOS COMUNES
113
Un posible diagrama de un reverberador en cuanto a estas dos
divisiones se muestra en la siguiente figura
Figura 6.7. División de un reverberador en secciones transitoria y
permanente
La sección transitoria de la respuesta impulsiva de un entorno
reverberante, también denominada reflexiones tempranas, suele tomarse
como los primeros 100 ms de la reverberación. Con mayor precisión, es el
tiempo hasta que la reverberación alcanza su comportamiento estadístico
asintótico. Dado que las reflexiones tempranas son relativamente dispersas
y consumen un tiempo pequeño pueden implementarse usando líneas de
retraso sin perjuicio del coste computacional.
Si existe suficiente potencia computacional, es preferible darle
carácter espacial y directivo a las reflexiones tempranas, pues es sabido que
las primeras reflexiones tienen una fuerte influencia en la impresión
espacial, es decir, la percepción del oyente de los ángulos o direcciones
desde donde se reciben los sonidos.
En la sección permanente, se modela la reverberación desde un punto
de vista perceptual, buscando un decaimiento y respuesta frecuencial
suaves pero no demasiado regular. Implementar un decaimiento
exponencial no presenta problemas, pues los sistemas lineales estables
exhiben dicho comportamiento de forma natural. El problema radica en
encontrar una respuesta suave aunque no demasiado regular para que el
efecto no resulte muy artificial, pues en caso de estar los modos
regularmente espaciados pueden generarse periodicidades audibles en la
respuesta impulsiva en el dominio temporal.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
6. EFECTOS DE SONIDOS COMUNES
114
Una señal que satisface las características anteriormente
mencionadas puede ser un ruido coloreado con decaimiento exponencial, y
con un factor de decaimiento de energía mayor a altas frecuencias que a
bajas. Un valor típico de densidad en la respuesta de reverberación tardía
puede ser de 1000 ecos por segundo, aunque para sonidos muy impulsivos
se necesitan casi 10000 ecos para lograr una respuesta suave.
Algunos parámetros de control deseables en un módulo de
reverberación incluyen:
t 60 ( f ) que es el tiempo de reverberación a cada frecuencia f y se
define como el tiempo que tarda en decaer la amplitud en 60 dB.
G 2 ( f ) o ganancia de potencia de señal a cada frecuencia
C ( f ) o claridad que se define como el cociente de energía entre las
reflexiones tempranas y tardías.
ρ ( f ) o coeficiente inter-aural entre oídos izquierdo y derecho.
Otras implementaciones
Una implementación con filtros pasa todo se debe a M. R. Schroeder,
quien en su trabajo Colorless Artificial Reverberation, sugiere el uso de
filtros pasa todo para implementar algoritmos de reverberación. Estos
elementos continúan siendo la base de dispositivos comerciales de
reverberación. La idea del uso de filtro pasa-todo es especialmente brillante
ya que no hay nada en la naturaleza del fenómeno de reverberación que
sugiera su uso. Un diagrama básico de un modelo de reverberación puede
verse en la siguiente figura:
Figura 6.8. Cascada de tres secciones pasa-todo.
Cada filtro pasa todo puede interpretarse como un elemento que
expande cada muestra de entrada no nula en una repuesta impulsiva
infinita. Aunque no es un modelo físico de reflexión difusa, las reflexiones
simples son extendidas en un conjunto de reflexiones, que es
cualitativamente lo que deseamos.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
6. EFECTOS DE SONIDOS COMUNES
115
Una implementación con FDN o redes de retardo realimentadas se
debe a M. A.. Gerzon. Un diagrama típico de una red de retardo
realimentada se muestra en la figura
Figura 6.9. Red de retraso realimentada.
La FDN puede verse como un filtro peine realimentado, obtenido
reemplazando la línea de retardo con una matriz diagonal y reemplazando
la ganancia de realimentación por el producto de una matriz diagonal con
una ortogonal
El diagrama anterior puede describirse analíticamente como:
(6.5)
El diseño de la matriz de realimentación Q se hace partiendo de un
prototipo sin pérdidas, es decir, con un tiempo de reverberación infinito y
trabajando hasta conseguir un generador de ruido con decaimiento
exponencial. El diseño de los retardo M i del FDN se realiza en base a
asegurar un densidad de modos los suficientemente alta en todas las bandas
de frecuencias. Una densidad de modos insuficientes puede dar lugar a la
aparición de tonos espúreos.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
6. EFECTOS DE SONIDOS COMUNES
116
Una regla empírica para fijar dichos retrasos es utilizar el camino
medio libre o mean free path. Dicho parámetro se define como la distancia
media que un rayo de sonido viaja antes de encontrar un obstáculo y
reflejarse. Un valor aproximado del parámetro para un auditorio
convencional puede estimarse como:
d =4
V
S
(6.6)
Donde V es el volumen de la habitación y S la superficie total
encerrada. Esta aproximación requiere la hipótesis de campo difuso, es
decir, que las ondas planas viajan aleatoriamente en cualquier dirección y
por tanto solo es válida para reverberaciones tardías. El valor de los
retrasos puede hallarse utilizando este valor según:
d
1
=
cT N
N
∑M
i =1
(6.7)
i
Donde c denota la velocidad del sonido y T el período de muestreo.
El valor obtenido debe tomarse como cota inferior para los retrasos, pues
en salas reales las reflexiones son a menudo difusas especialmente a altas
frecuencias.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
6. EFECTOS DE SONIDOS COMUNES
117
6.2. Otros efectos
Vibrato
El término vibrato hace pequeñas variaciones cuasi-periódicas en el
pitch o frecuencia fundamental de un tono. Este efecto es musicalmente
muy importante en los instrumentos de cuerda frotada y en la voz humana.
En los instrumentos de cuerda frotada, el vibrato se produce haciendo
vibrar el dedo que sostiene el tono en el diapasón y en la voz humana se
consigue modulando la tensión de las cuerdas vocales. El vibrato suele ir
acompañado del trémolo que consiste en una modulación en amplitud a la
misma frecuencia que el vibrato que lo causa.
Para aplicar vibrato a un sonido, es necesario aplicar un salto de
frecuencia cuasi-periódico. Esto puede implementarse usando una línea de
retraso variable que introduce un efecto Doppler que puede interpretarse
musicalmente como un vibrato, es decir una pequeña modulación en
frecuencia.
Si llamamos x(t) a la entrada a una línea de retraso variable, la salida
puede escribirse como:
y (t ) = x(t − Dt )
(6.8)
Donde Dt representa el retraso variable en tiempo. En
implementaciones discretas cuando Dt no es un múltiplo entero del
intervalo de muestreo, x(t − Dt ) puede aproximarse siguiendo algún método
de interpolación. Analicemos ahora el salto en frecuencia causado por un
retraso variable en tiempo para una sinusoide compleja de frecuencia ω s ,
x (t ) = e
jst
La salida es ahora
y (t ) = x(t − Dt ) = e jω s ( t − Dt )
(6.9)
La frecuencia instantánea de esta señal es
ω l = ω s (1 −
d
Dt )
dt
(6.10)
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
6. EFECTOS DE SONIDOS COMUNES
118
Por tanto, la tasa de crecimiento del retraso proporciona el salto
relativo en frecuencia:
ω − ωl
d
Dt = s
dt
ωs
(6.11)
Comparamos ahora esta ecuación con la ecuación del efecto
Doppler para un sistema de fuente-receptor
v ls
c
ωl = ω s
v sl
1−
c
1+
(6.12)
Donde ω s es la frecuencia emitida por la fuente en reposo, ωl es la
frecuencia percibida por el oyente, vls representa la velocidad del oyente
relativa al medio en dirección a la fuente y v sl simboliza la velocidad de la
fuente relativa al medio en dirección al oyente.
Como resultado de la comparación, encontramos que el retraso
variable simula naturalmente un efecto Doppler causado por un oyente
móvil con velocidad
v ls = −
1 d
Dt
c dt
(6.13)
Es decir, que la velocidad de variación del retraso, provoca un efecto
análogo a un movimiento relativo entre fuente sonora y oyente, lo que a su
vez provoca el efecto vibrato buscado
Chorus
El efecto chorus o choralizer consiste en un procesamiento de señal
que consigue a partir de una sola fuente sonora, muchas fuentes sonoras
sonando al unísono. Este efecto es muy interesante a la hora de sintetizar el
sonido de una sección de cuerdas a partir de la muestra de un único
instrumento de la sección. Dado que la ejecución al unísono nunca es
exacta (si lo fuera solo tendríamos un aumento del amplitud de la fuente
sonora inicial, pero no cambiaría su cualidad tímbrica), el efecto chorus se
simula sumando copias con modificaciones independientes entre sí. Dichas
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
6. EFECTOS DE SONIDOS COMUNES
119
modificaciones pueden incluir retrasos, saltos en frecuencia y/o modulación
en amplitud.
El efecto chorus suele implementarse usando líneas de retraso
variable con múltiples tomas de señal. Dichas salidas pueden oscilar
respecto a su posición consiguiendo introducir una cierta aleatoriedad que
da la cualidad natural necesaria a una sección de instrumentos tocando al
unísono.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
7. EVOLUCIÓN Y FUTURO DE LAS TÉCNICAS DE SÍNTESIS
120
7. Evolución y futuro de las técnicas de síntesis.
Historia de la Síntesis de Sonidos Musicales
La historia de la síntesis artificial de sonidos musicales se remonta a
fechas tan tempranas como 1860, año en que Helmholtz, pionero en el uso
de dispositivos eléctricos para generar sonidos, diseña un conjunto de
osciladores electromecánicos. Estos dispositivos generaban sonidos simples
senoidales, es decir tonos puros.
En 1897, Thaddeus Cahill desarrolla un sistema de generación de
sonido electrónico denominado Dynamophone o Telharmonium. El
instrumento se basaba en el uso de dinamos modificadas eléctricamente,
produciendo corrientes alternas de diferentes audiofrecuencias. Estas
señales pasaban mediante un teclado y un panel de control a una serie de
receptores telefónicos provistos de tonos acústicos especiales. El aparato
completo pesaba acerca de unas 200 toneladas con una longitud de casi 20
metros.
En 1920, Leon Theremin, inventa y desarrolla un instrumento
musical electrónico, el Theramín, que se controla mediante la posición de
las manos del intérprete. Este instrumento generaba un sonido abstracto, no
encontrado en la naturaleza, que cautivó a algunos compositores los cuales
incluso llegaron a escribir algunas obras para dicho instrumento en
concreto.
El piano Neo-Bechstein inventado en 1931, era todavía un piano
acústico modificado para capturar las vibraciones producidas naturalmente
y someterlas a modificaciones y amplificaciones electrónicas
El primer intento más serio de un instrumento electrónico llega con
el Órgano Hammond, que aparece en 1935 de mano de Laurens Hammond
y gana rápidamente un puesto de honor en la historia de los instrumentos
musicales sintéticos por su peculiar, aunque no enteramente auténtica,
calidad del sonido. El principio de generación del sonido se basaba en la
rotación de piezas circulares en un campo magnético y utilizaba técnicas de
síntesis aditiva.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
7. EVOLUCIÓN Y FUTURO DE LAS TÉCNICAS DE SÍNTESIS
121
Como los primeros osciladores de Helmholtz, todos estos
sintetizadores pioneros eran sintetizadores analógicos. Con la llegada de los
transistores electrónicos en 1950, la tecnología controlada por tensión
revoluciona las técnicas de síntesis.
Basándose en esta nueva tecnología, Harald Bode desarrolla el
Melochord en 1961, el primer sintetizador controlado por tensión. En 1964
Robert Moog y Donald Buchla desarrollan independientemente las
primeras versiones comerciales de sintetizadores electrónicos.
En los años 70, el aumento de la demanda provoca el nacimiento de
nuevas compañías dedicadas a la síntesis de sonido, alguna de las cuales
llega hasta nuestros días como Oberheim, E-mu y Roland Corporation.
En 1960, John Chowning comienza a investigar detalladamente las
características de los sonidos de frecuencia modulada usando síntesis
computacional, pero no es hasta 1973, con la aparición de su famoso
trabajo Síntesis de espectros complejos de audio mediante Modulación en
Frecuencia, cuando se presta atención a la posibilidad de sintetizar timbres
instrumentales con la adecuada combinación de parámetros FM. En 1976
aparecen los primeros instrumentos Yamaha basados en esta técnica de
síntesis.
En 1975 y paralelamente, la New England Digital Corporation,
produce el prototipo de un sintetizador digital, comercializado
posteriormente con el nombre de Synclavier, un o de los más avanzados
comparados con sus antecesores.
En 1979, se introduce en el mercado el Fairlight CMI, primer
instrumento con teclado de 6 octavas y controles de pedal. Permitía
diferentes tipos de síntesis como síntesis aditiva, sustractiva e incluso
PCM.
En el mismo año, Digital Music Systems produce el primer chip
integrado para síntesis de sonido el DMX-1000, a partir de este momento
las tecnologías LSI (Large Scale Integration), han reducido estos DSPs al
tamaño de un chip de silicio, apareciendo instrumentos mucho más
eficientes y flexibles. Además, en 1982 se especifica el protocolo MIDI lo
que permite una implementación más portable. Durante la década de los 80
aparecen los instrumentos electrónicos Casio y Kawai que acaparan el
mercado de los sintetizadores de gama media.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
7. EVOLUCIÓN Y FUTURO DE LAS TÉCNICAS DE SÍNTESIS
122
En esta década, los grandes avances en tecnología digital producen
modelos de síntesis más realistas y baratos. Durante esta década, el avance
más significativo en los modelos de síntesis viene marcado por la evolución
de las tarjetas de sonido de los PCs. Desde las primeras tarjetas que
aparecen en el mercado como la AdLib o la SoundBlaster que implementan
síntesis FM, la tecnología de las tarjetas comienza a orientarse hacia la
síntesis PCM como la Turtle Beach Multisound o la Gravis Ultrasound
(GUS), primer intento de fabricar un sampler para el mercado doméstico.
En la década de los 90, los modelos computacionalmente más
costosos como los modelos físicos, comienzan a ser realizables y
comercializables a nivel de usuario. El primer sintetizador comercial que
implementa esta tecnología es desarrollado por Yamaha en 1971, tras un
acuerdo con la universidad de Stanford, pionera en el desarrollo de la
síntesis por guiaonda digital. El sintetizador recibe el nombre de Yamaha
VL1.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
7. EVOLUCIÓN Y FUTURO DE LAS TÉCNICAS DE SÍNTESIS
123
Futuro de los modelos de síntesis
Un ordenador convenientemente programado, es virtualmente capaz
de producir cualquier sonido imaginable, familiar o inaudito. La dificultad
consiste en decirle como hacerlo o en describir de alguna forma, el sonido
que buscamos. Los nuevos métodos de síntesis sonora, tienden por ello a
ser más sofisticados en sus posibilidades, pero buscan interfaces de control
más intuitivos. En cualquier caso, el problema del uso de CPUs para
síntesis de instrumentos es el problema de no poder trabajar en tiempo real.
Sin embargo, la creciente potencia de los procesadores actuales va a
cambiar en breve este panorama, con la implantación de métodos de
síntesis por software en tiempo real. Actualmente, existen ya en el mercado
varios programas para PC, que emulan por software (y por una décima
parte de su precio en hardware) las prestaciones de sintetizadores
profesionales y que, lo único que requieren es el conversor D/A que se
encuentra en cualquier tarjeta de sonido de 16 bits.
Así que es posible vaticinar que el futuro de los métodos de síntesis
se encamina hacia la síntesis por software y es posible que los futuros
instrumentos electrónicos sean una especie de pequeños ordenadores
procesando los algoritmos de síntesis más complejos que se pueda
imaginar.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
8. ANÁLISIS Y SÍNTESIS DE SONIDOS DE PIANO
124
8. ANÁLISIS Y SÍNTESIS DE SONIDOS DE PIANO
8.1. Análisis de sonidos PCM
El siguiente sonido es una muestra del Do central C4 de un piano
comercial Roland HP 237que implementa síntesis PCM
Figura 8.1. Forma de onda para la nota C4 obtenida por muestreo
En la figura se observan claramente dos regiones diferenciadas, una
región transitoria relacionada con el ataque de tecla denominada attack y
otra permanente denominada sustain. Como ya se discutió en el capítulo 2,
dichas secciones no se diferencian solo en la potencia sonora, sino que son
de naturaleza armónica bien distinta.
Si analizamos por separado ambas regiones, observamos que tanto la
forma de onda como el contenido espectral de cada sonido son distintos.
Figura 8.2 Forma de onda análisis espectral de la sección attack
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
8. ANÁLISIS Y SÍNTESIS DE SONIDOS DE PIANO
125
Figura. 8.3 Forma de onda y análisis espectral de la sección sustain
Puede observarse que la sección attack posee un contenido espectral
más amplio variando inclusa la amplitud relativa de los armónicos que
tanto influye en el timbre generado.
La forma de onda es esencialmente distinta aunque puede apreciarse
que ambas generan la misma frecuencia, la del do central del piano, que en
relación con el La A4 de referencia a 440 Hz está a una distancia de sexta
mayor, lo que equivale a 4 tonos y un semitono, es decir, 9 semitonos, lo
que proporciona una frecuencia de:
C 4(12 2 ) 9 = A4
C 4 = 440(12 2 ) −9 = 261.62 Hz
Lo que está en consonancia con los armónicos obtenidos en la figura
anterior.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
8. ANÁLISIS Y SÍNTESIS DE SONIDOS DE PIANO
126
Para poner de manifiesto las limitaciones del desplazamiento de
pitch, generaremos a partir de este C4 muestreado un G4 a distancia de
quinta justa, lo que supone un desplazamiento en frecuencia de 1.5 y
compararemos la forma de onda obtenida por el desplazamiento de pitch y
la obtenida directamente por muestreo del piano Roland
Figura 8.4. Forma de onda para la nota G4 obtenida mediante muestreo
directo del piano Roland
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
8. ANÁLISIS Y SÍNTESIS DE SONIDOS DE PIANO
127
Figura 8.5. Análisis temporal y frecuencial de la forma de onda en sus
secciones Attack y Sustain
Veamos ahora la forma de onda para la misma nota G4 pero
generada por el desplazamiento de pitch de 1.5
Figura 8.6. Forma de onda para la nota G4 obtenida por pitch shifting
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
8. ANÁLISIS Y SÍNTESIS DE SONIDOS DE PIANO
128
Figura 8.7. Análisis temporal y frecuencial de la forma de onda.
Como puede observarse comparando las figuras 8.5. y 8.7., las
formas de onda son esencialmente diferentes. La forma de onda obtenida
por pitch shifting no es más que la compresión en tiempo de la forma de
onda de la nota C4 y por consiguiente la dilatación en frecuencia del
espectro de la nota C4 representado en las figuras 8.2. y 8.3.
Cuando el desplazamiento de pitch es de unos pocos semitonos, la
diferencia entre los espectros no es audible. Pero para este caso, 9
semitonos, el tono generado tendrá un sonido metálico desagradable que no
puede utilizarse para una interpretación musical artística.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
8. ANÁLISIS Y SÍNTESIS DE SONIDOS DE PIANO
129
8.2. Análisis de sonidos FM
El sonido presentado en la siguiente figura corresponde a la misma nota C4
pero proveniente del muestreo de un teclado Casio que implementa síntesis
PD, variante de FM.
Figura 8.8. Forma de onda de la nota C4 proveniente de síntesis PD
Figura 8.9. Análisis temporal y espectral de la forma de onda
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
8. ANÁLISIS Y SÍNTESIS DE SONIDOS DE PIANO
130
Como puede observarse, en el caso de síntesis PD, la sección attack y
sustain solo presentan diferencias de amplitud y en la envolvente, pero no
en la forma de onda que es exactamente la misma. Esto hace que el sonido
generado no presenta tanta naturalidad. Sin embargo, la comparación entre
los dos análisis espectrales, muestra que la síntesis es bastante acertada. De
hecho la audición de ambos sonidos muestra que el resultado de la síntesis
PD, presenta cualidades muy agradables al oído.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
8. ANÁLISIS Y SÍNTESIS DE SONIDOS DE PIANO
131
8.3. Síntesis de sonidos FM
Por último, como muestra de la implementación práctica de un
modelo de síntesis, se analizarán algunos sonidos generados por síntesis
FM con ayuda del programa FM Dream, de código abierto OpenSource y
sin problema alguno de licencia para su utilización.
Se ha elegido FM por ser uno de los modelos más sencillos de
implementar. Solo necesitamos un conjunto de generadores de onda en este
caso 4, interconectados entre sí siguiendo un patrón que se denomina
algoritmo. De hecho, este es el mecanismo interno de funcionamiento
interno de los sintetizadores comerciales. Una vez fijado el número de
algoritmo, es decir, la interconexión de los osciladores, y los parámetros de
modulación de cada uno de ellos, se determina completamente la forma de
onda resultante
Figura. 8.10. Vista general del programa FM Dreams
Para cada oscilador puede elegirse la amplitud en un rango de
valores 0-32765 (15 bits). El parámetro Feed In permite especificar el
índice de modulación para las uniones FM o bien la ponderación en las
uniones aditivas. También puede especificarse para cada oscilador la
envolvente ADSR. El programa permite además añadir filtrado de varios
tipos para mejorar las respuestas.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
8. ANÁLISIS Y SÍNTESIS DE SONIDOS DE PIANO
132
Con este ejemplo de síntesis se ponen de manifiesto el principal
inconveniente a la hora de usar un modelo no lineal, es decir, la falta de
relación directa observable causa-efecto. Debido a las relaciones complejas
y no-lineales que intervienen en la formación del espectro FM, el cambio
uniforme de los parámetros, no asegura la variación uniforme del espectro
en un único sentido, lo que hace de FM un método fundamentalmente
heurístico y empírico.
En definitiva, por ensayo-error y variando los parámetros del
modelo, se obtuvieron algunos sonidos interesantes que se asemejan a un
sonido de piano.
Por comparación directa de los espectros resultante y deseado, se
obtuvieron para el piano los siguientes parámetros:
A1 = 100%
A2 = 50%
f c1 = 220 Hz
f c 2 = 220 Hz
f m1 = 220 Hz
f m 2 = 440 Hz
I 1 = 85 → β = 1.2
I 2 = 50 → β = 1.1
Donde A1 y A2 se refieren a la ponderación de la unión aditiva (línea
continua en el dibujo) mientras que f m1 , f c1 , f m 2 , f c 2 corresponden a los
osciladores 1, 2, 3 y 4 respectivamente. Para el segundo oscilador se eligió
una frecuencia moduladora que fuera múltiplo de la frecuencia de la nota a
generar La-3 a 220 Hz. Se observaron mejores resultados ajustando la
frecuencia moduladora a un múltiplo mayor, más allá del armónico 10,
como 2860 ó 3080 Hz, para tener mayor riqueza espectral.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
8. ANÁLISIS Y SÍNTESIS DE SONIDOS DE PIANO
133
La envolvente ADSR se ajustó de forma que el sonido resultara lo
más agradable posible. El análisis espectral del sonido obtenido se muestra
en la siguiente figura.
Figura. 8.11. Análisis temporal y espectral de la forma de onda buscada
Dejando al margen la componente de continua, que supone
solamente un nivel de offset de la señal, tenemos dos picos principales a
220Hz y 440Hz como corresponde al tono de piano. Sin embargo, no fue
posible modificar convenientemente el nivel del resto de los armónicos. Es
por ello que el sonido no resulta del todo realista. Para ello hubiera sido
necesaria la intervención de un tercer oscilador. De hecho, el algoritmo
utilizado por Yamaha para el sintetizador DX-7 para sonidos de piano
emplea efectivamente seis osciladores en un algoritmo de adición.
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
BIBLIOGRAFÍA
134
BIBLIOGRAFIA
Askenfelt A., ed., “Five Lectures on the Acoustics of the Piano,”
Stockholm: Royal Swedish Academy of Music, 1990,
Bate J., "The Effects of Modulator Phase on Timbres in FM Synthesis,"
Computer Music Journal 14(3), 1990.
Bristow-Johnson R., “Wavetable Synthesis, A Fundamental Perspective”,
Wave Mechanics, Inc.
Chiantore L.. “Historia de la Técnica Pianística”, Alianza Editorial, 2001
Chowning J., "The Synthesis of Complex Audio Spectra by Means of
Frequency Modulation," Journal of the Audio Engineering Society 21(7),
1973; reprinted in Computer Music Journal 1(2), 1977.
De Furia S. y ScaciaFerro J. “The Midi Resource Book”, Third Earth
Publishing Inc.
1987
Hiller L. y Ruiz P., “Synthesizing Musical Sounds by Solving the Wave
Equation for Vibrating Objects”, Journal of the Audio Engineering
Society, 1971.
Karplus K. y Strong A., “Digital Synthesis of Plucked-String und Drum
Timbres”, Computer Music Journal, 1983
Piston W., “Armonía”, SpanPress Universitaria, 1998
Serra X. and Smith J.O., “Spectral modeling synthesis: a sound
analysis/synthesis system based on a deterministic plus stochastic
decomposition”, Computer Music Journal, 1990.
Smith J.O., “Music applications of digital waveguides”, Technical Report
STANM-39 CCRMA.
Smith J.O., “Viewpoints on the story of digital synthesis”, Proceedings of
the International Computer Music Conference
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
BIBLIOGRAFÍA
135
Smith J.O., “Physical modeling using diigtal waveguides”, Computer
Music Journal
Smyth T., “Fundamentals of Computerized Sound”, Computing Science,
Simon Fraser University Essays Online
Truax B., "Organizational Techniques for C:M Ratios in Frequency
Modulation", Computer Music Journal, 1(4), 1978, pp. 39-45; reprinted in
Foundations of Computer Music, C. Roads and J. Strawn (eds.). MIT Press,
1985.
“Acoustical Society of America, Publications”
http://asa.aip.org/publications.html
“Harmony Central: The Keyboards
http://harmonycentral.com/Synth/Data/
and
Synths
Database”,
“Music DSP Source Code Archive”, http://musicdsp.org/
Smith J.O., “Physical Audio Signal Processing Digital Waveguide
Modeling
of
Musical
Instruments
and
Audio
Effects”
http://ccrma.stanford.edu/~jos/waveguide/waveguide.html
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
APÉNDICE
136
APÉNDICE
En el apéndice se incluyen los códigos Matlab necesarios para el
análisis temporal y frecuencial así como para el mecanismo de
desplazamiento de pitch de la síntesis PCM.
Cortar.m
%Funcion utilizada para seleccionar una seccion concreta
% de una funcion utilizando el raton.
% Devuelve tanto el intervalo temporal seleccionado como los valores
function [tc,Yc]=cortar(Y,Fs)
Ts=1/Fs;
t=0:Ts:(length(Y)-1)*Ts;
plot(t,Y);
Ts=1/Fs;
p=ginput(2);
Yc=Y(round(p(1,1)/Ts):round(p(2,1)/Ts));
tc=round(p(1,1)/Ts)*Ts:Ts:round(p(2,1)/Ts)*Ts;
Despitch.m
% Funcion que implementa el desplazamiento de Pitch.
% El resultado es una señal YN con una frecuencia N veces
% superior a la señal Y
function YN=despitch(Y,N)
j=1;
i=1;
YN(j)=Y(i);
while(i<length(Y)-1)
i=i+N;
j=j+1;
n=floor(i);
f=i-n;
YN(j)=f*Y(n+1)+(1-f)*Y(n);
end
YN=YN';
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
APÉNDICE
137
Separa.m
% Funcion utilizada para separar la seccion permanente de la transitoria
% El usuario debe seleccionarlas con el raton asi como los periodos
% que se utilizaran para representarla
function [tFtran,Ftran,tFperm,Fperm,Ytran,Yperm]=separa(Y,Fs);
figure
[ttran,Ytran]=cortar(Y,Fs);
[tperm,Yperm]=cortar(Y,Fs);
[tFtran,Ftran]=cortar(Ytran,Fs);
[tFperm,Fperm]=cortar(Yperm,Fs);
tFtran=tFtran+ttran(1);
tFperm=tFperm+tperm(1);
figure(1);
Subplot(411);plot(ttran,Ytran);
Subplot(412);plot(tperm,Yperm);
Subplot(413);plot(tFtran,Ftran);
Subplot(414);plot(tFperm,Fperm);
Fftzoom.m
% Funcion que realiza el analisis frecuencial de las secciones
% transitoria y permanente que se seleccionan con la funcion separa
% El programa desplaza la fft para represantarla de -Pi a Pi
% y permite un zoom para representar de -Fmax a Fmax en lugar de -Fs/2 a
% Fs/2
function [Y1,Y2]=fftzoom(Y,Fs,Fmax);
[tFtran,Ftran,tFperm,Fperm,Ytran,Yperm]=separa(Y,Fs);
M1=length(Ftran);
M2=length(Fperm);
M=min([M1 M2]);
Ftran=Ftran(1:M);
tFtran=tFtran(1:M);
Fperm=Fperm(1:M);
tFperm=tFperm(1:M);
close all
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
APÉNDICE
138
figure(1)
y1=Ytran;
y2=Yperm;
Subplot(411);plot(tFtran,Ftran);
Subplot(412);plot(tFperm,Fperm);
N=2*length(Yperm);
Y1=abs(fft(y1,N));
Y1=Y1/max(Y1);
Y1t=[Y1(round(length(Y1)/2):length(Y1)); Y1(1:round(length(Y1)/2)-1)];
Y2=abs(fft(y2,N));
Y2=Y2/max(Y2);
Y2t=[Y2(round(length(Y2)/2:length(Y2))); Y2(1:round(length(Y2)/2)-1)];
F=-Fs/2:Fs/N:Fs/2-1/N;
Subplot(413);plot(F(round(length(F)/2)Fmax:round(length(F)/2)+Fmax),Y1t(round(length(Y1t)/2)Fmax:round(length(Y1t)/2)+Fmax));
Subplot(414);plot(F(round(length(F)/2)Fmax:round(length(F)/2)+Fmax),Y2t(round(length(Y2t)/2)Fmax:round(length(Y2t)/2)+Fmax));
%La frecuencia maxima a representar es Fs/2
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS
AGRADECIMIENTOS
139
AGRADECIMIENTOS
Finalmente, quisiera expresar mi agradecimiento a las personas que
me ayudaron durante el desarrollo de este trabajo.
En primer lugar, a mi madre y a mi padre, por el sólido apoyo y la
indiscutible confianza que siempre han depositado en mí.
A mi tutor, D. Rubén Martín Clemente, por darme la posibilidad de
realizar un trabajo en el que uniera dos de mis disciplinas más queridas: el
Tratamiento Digital de Señales y la Música, y en general a todos los
profesores de la Escuela Superior de Ingenieros, que supieron estimularme
intelectualmente y académicamente para llegar hasta aquí.
A mis amigos, algunos de ellos futuros compañeros de profesión, por
la ayuda y el apoyo prestado, tanto académico como moral y humano, éste
último inestimable en el mundo tan competitivo en que vivimos.
Por último, y no menos importante, a mis profesores del
Conservatorio de Música, que me enseñaron a valorar, no sólo el aspecto
científico y tecnológico de la realidad, sino también la importancia del Arte
y las disciplinas humanísticas en el desarrollo personal, inculcando en mí el
amor a la Música y el gusto por lo estético.
En definitiva, a la Música misma, nuestra amada inmortal sin la cual,
en palabras de Nietzsche, la Vida sería un error….
SÍNTESIS DIGITAL DE INSTRUMENTOS MUSICALES
SÍNTESIS DIGITAL DE PIANOS ELECTRÓNICOS