b) p ^ [ qv

I OLIMPIADA HUMTEC DE MATEMÁTICA - OHM 2015
CUARTO AÑO DE SECUNDARIA
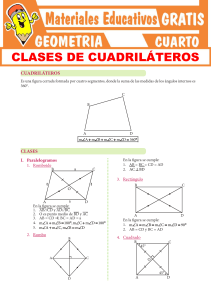
1.
Indica la proposición que representa el siguiente circuito:
a) p v [ q v (p ^ r) ]
b) p ^ [ q v (p ^ r) ]
c) p v [ q ^ (p v r) ]
d) p v [ q v (p v r) ]
2.
Simboliza proporcionalmente lo siguiente:
“Es falso que si Luis no se compra una camisa no podrá ir a la fiesta, además no
bailará”.
*n es negación.
a) n(np <--> nq ) ^ nq
b) n(np --> nq )
^
nr
c) n(np <--> nq ) ^ nr
d) n(np --> nr )
3.
^
nr
Si f(x) = √3 − 𝑥 y g(x) = √𝑥 + 1 . Halla el dominio de f(x) + g(x).
a) {-2; 3}
b) {-1; -3}
c) {-1; 3}
d) {1; -2}
4.
Sobre un tablero de ajedrez se colocan algunos granos de trigo del siguiente modo:
En el primer cuadro se coloca un grano, en el segundo el doble que en el primero, en
el tercero el doble que en el segundo y así sucesivamente. ¿Cuántos granos de trigos
serán necesarios para cubrir los 64 casilleros del tablero?
a) 26
b) 364
c) 264 -2
d) 264 -1
5.
Calcula el promedio aritmético de los términos de la progresión aritmética:
17; 24; 31;…; 220
a)
b)
c)
d)
6.
116,3
118
118,5
120,5
Calcula el número total de diagonales de aquel polígono convexo en el cual la suma
de las medidas de los ángulos interiores y exteriores es 2700°.
a) 94
b) 90
c) 96
d) 92
7.
El segmento de medida comprendido entre las diagonales de un trapecio mide 48 cm.
Halla la longitud de la mediana si la base menor del trapecio es la quinta parte de la
base mayor.
a) 74
b) 72
c) 76
d) 71
8.
Del gráfico, calcula los valores de x e y.
a) 110° y 90°
b) 120° y 90°
c) 120° y 80°
d)100° y 80°
9.
En un ∆ FAG, FA > AG se trazan las bisectrices interior AD y exterior AE. Calcula EG,
si FD =12 y DG =9.
a) 64
b) 63
c) 62
d) 61
10.
En la figura, O es centro de la circunferencia, FM ⊥ AC; BP = 6 cm, PH = 4 cm y HC =
24 cm. Halla AB.
a) 35
b) 38
c) 32
d) 36
11.
En un ∆ ARP, F Є AR y G Є RP de tal manera que AF: FR = 5:2 y FG // AP. Calcula el
área de la región FRG, si la región AFGP tiene 72 𝑢2 .
a) 5,4 𝑢2
b) 4,6 𝑢2
c) 6,2 𝑢2
d) 6,4 𝑢2
12.
ABCD es un trapecio, BC // AD y las diagonales se intersecan en el punto O. Calcula el
área de la región triangular AOB, si la región COD tiene área 12 𝑢2 .
a) 11 𝑢2
b) 14 𝑢2
c) 12 𝑢2
d) 13𝑢2
13.
ABCD es un rombo donde M es un punto medio de BC y AM corta a la diagonal BD en
el punto R. Si RM =2 m y m<BRM = 45°, calcula el área del rombo.
a) 45 𝑚2
b) 47𝑚2
c) 46 𝑚2
d) 48 𝑚2
14.
En un ΔABC, se traza la bisectriz interior AF y luego RF // AC; estando R en AB, calcula
RF, si AB =14 y AC =6.
a) 4,6
b) 4,2
c) 2,4
d) 5,6
15.
ABCD es un trapecio isósceles; AD // BC y la diagonal es perpendicular a CD. Si BC = 7
y AD = 25, calcula AB.
a) 16
b) 14
c) 15
d) 12
16.
Un vendedor de libros acuerda en su contrato lo siguiente: Si diariamente vende 12
libros recibe una comisión de S/. 60 y si vende 15 libros recibe una comisión de S/.75.
Cierto día vendió 20 libros, ¿cuánto recibirá de comisión?
a) 100 soles
b) 110 soles
c) 102 soles
d) 113 soles
17.
Un grupo de obreros demora 6 días en hacer una obra. ¿Cuánto demoraría otro grupo
de obreros 20% más eficiente?
a) 6 días
b) 5 días
c) 4 días
d) 12días
18.
En una reunión hay 1000 personas de las cuales el 60% son hombres. Se sabe que el
5% de los hombres usan anteojos y el 4% de las mujeres usan anteojos. ¿Cuántas
personas en la reunión usan anteojos?
a) 48
b) 45
c) 44
d) 46
19.
En la figura, halla el valor de x.
a)
b)
c)
d)
20.
60°
70°
80°
72°
Halla el perímetro de la siguiente figura.
*Todos los ángulos son rectos.
a) 48
b) 45
c) 44
d) 42
CLAVES DE RESPUESTAS 4° DE SECUNDARIA
N° DE PREGUNTA
CLAVE
1
a
2
b
3
c
4
d
5
c
6
b
7
b
8
c
9
b
10
d
11
d
12
c
13
d
14
b
15
c
16
a
17
b
18
d
19
c
20
d